吴恩达机器学习入门笔记6-决策树(由西瓜书补充)
6 决策树
6.1 结构
- 一个根节点:样本全集
- 若干个内部结点:对应于属性测试
- 若干个叶结点:决策结果
- 属性代表了各个结点,各个结点的连接线代表属性的取值
- 当第一层最优划分属性选取后,在划分后的D中进行递归,一层层选取最优划分属性,最后形成决策树
- 只有一层划分的决策树称为决策树桩
6.2 目的
产生一颗泛化能力强,即处理未见示例能力强的决策树
6.3 衡量划分属性的标准
随着划分的不断进行,决策树的分支结点包含的样本尽可能属于同一类别,即结点纯度应越来越高
6.3.1 ID3决策树-信息增益准则
- D的信息熵定义为
(6.1) E n t ( D ) = − ∑ k = 1 ∣ y ∣ p k l o g 2 p k Ent(D)=-\sum_{k=1}^{|y|}{p_klog_2p_k}\tag{6.1} Ent(D)=−k=1∑∣y∣pklog2pk(6.1)
D为当前样本集合, p k p_k pk为D中第k类样本占总样本比例**(依照标记分类)**。信息熵越小,D纯度越高
- 属性a对D划分所得的信息增益定义为
(6.2) G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V ∣ D v ∣ D E n t ( D v ) Gain(D,a)=Ent(D)-\sum_{v=1}^{V}\frac{|D^v|}{D}Ent(D^v)\tag{6.2} Gain(D,a)=Ent(D)−v=1∑VD∣Dv∣Ent(Dv)(6.2)
D v D^v Dv为用离散属性 a = a= a={ a 1 , a 2 , … , a V a^1,a^2,\dots,a^V a1,a2,…,aV}划分后在属性 a V a^V aV上的样本。信息增益越大,意味着用属性a划分所得纯度提升越大。因此最优划分算法为
(6.3) a ∗ = arg max a ∈ A Gain ( D , a ) a_*=\underset{a \in A}{\arg \max}\text{Gain}(D,a)\tag{6.3} a∗=a∈AargmaxGain(D,a)(6.3)
6.3.2 C4.5决策树-增益率准则
信息增益准则对可取值数目较多的属性有所偏好,为减少这种不利影响,C4.5决策树算法使用增益率选取最优划分属性,增益率定义为
KaTeX parse error: Expected '}', got '_' at position 12: \text{Gain_̲ratio}(D,a)=\fr…
其中
(6.5) IV ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ l o g 2 ∣ D v ∣ ∣ D ∣ \text{IV}(a)=-\sum_{v=1}^{V}\frac{|D^v|}{|D|}log_2\frac{|D^v|}{|D|}\tag{6.5} IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣(6.5)
成为属性a的固有值,属性a可能取值数目V越大,IV越大
-
对可取值数目较少的属性有所偏好,先从划分属性中找到信息增益高于平均水平的属性**,再从中选取增益率最高**的作为最优划分属性,最优划分算法为
-
KaTeX parse error: Expected '}', got '_' at position 44: …\max}\text{Gain_̲ratio}(D,a),\te…
6.3.3 CART决策树-基尼指数准测
- 数据集D的纯度用基尼指数衡量
(6.7) Gini ( D ) = ∑ k = 1 ∣ y ∣ ∑ k ′ ≠ k p k p k ′ = 1 − ∑ k = 1 ∣ y ∣ p k 2 \text{Gini}(D)=\sum_{k=1}^{|y|}\sum_{k'\ne k}p_kp_{k'}=1-\sum_{k=1}^{|y|}p_k^2\tag{6.7} Gini(D)=k=1∑∣y∣k′̸=k∑pkpk′=1−k=1∑∣y∣pk2(6.7)
基尼指数反应了从数据集D中随机抽取两个样本,其类别标记不一致的概率。因此基尼指数越小,D纯度越高
- 属性a的基尼指数定义为
(6.8) Gin_index ( D , a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ Gini ( D v ) \text{Gin\_index}(D,a)=\sum_{v=1}^V\frac{|D^v|}{|D|}\text{Gini}(D^v)\tag{6.8} Gin_index(D,a)=v=1∑V∣D∣∣Dv∣Gini(Dv)(6.8)
因此在候选属性集合A中,选择使得划分后基尼指数最小的属性为最优划分属性即
(6.9) a ∗ = arg min a ∈ A Gini_index ( D , a ) a_*=\underset{a \in A}{\arg \min}\text{Gini\_index}(D,a)\tag{6.9} a∗=a∈AargminGini_index(D,a)(6.9)
6.4 剪枝处理
结点划分过程不断重复,有时导致决策树分支过多,把训练集自身的特点当作所有数据具有的一般性质导致过拟合,因此可主动去掉一些分支降低过拟合的风险
6.4.1 预剪枝
决策树生成中,对每个结点在划分前先进行估计,若当前结点不能带来决策树的泛化性能提升,则停止划分并将当前结点标记为叶结点
- 会使决策树很多分支没有展开,降低过拟合风险,提升欠拟合风险
6.4.2 后剪枝
先从训练集生成一颗完整的决策树,然后自底向上对非叶结点进行考察,若将该结点对应子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为叶结点
- 后剪枝通常比预剪枝决策树保留更多分支,欠拟合风险很小,泛化性能往往优于预剪枝决策树,但训练时间比未剪枝与预剪枝决策树大得多
6.5 连续值与缺失值
6.5.1 连续值处理
计算样本中相邻属性的中位值作为划分点t,计算不同t时的信息增益,取最大值时的t作为划分点
(6.10) Gain ( D , a ) = max t ∈ T a Gain ( D , a , t ) = max t ∈ T a Ent ( D ) − ∑ λ ∈ { − , + } ∣ D t λ ∣ ∣ D ∣ Ent ( D t λ ) \begin{aligned} \text{Gain}(D,a)&=\max_{t\in T_a}\text{Gain}(D,a,t)\\ &=\max_{t\in T_a}\text{Ent}(D)-\sum_{\lambda\in\{-,+\}}\frac{|D_t^\lambda|}{|D|}\text{Ent}(D_t^\lambda) \end{aligned}\tag{6.10} Gain(D,a)=t∈TamaxGain(D,a,t)=t∈TamaxEnt(D)−λ∈{−,+}∑∣D∣∣Dtλ∣Ent(Dtλ)(6.10)
6.5.2 缺失值处理
-
在属性值缺失下进行划分属性选择
推广信息增益计算式
-
划分属性给定,对属性值缺失的样本进行划分
按照不同取值样本数目个数作为权值在各个属性取值均有划分
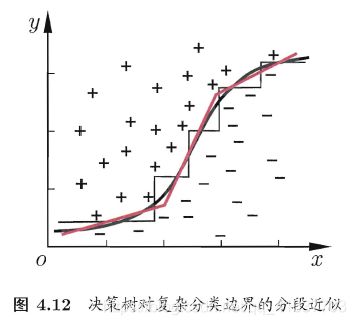
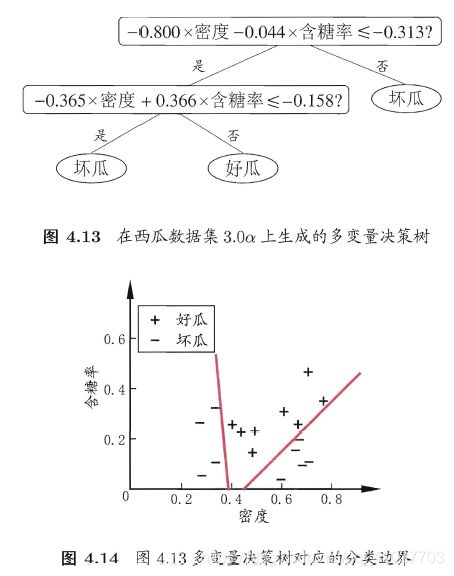
6.6 多变量决策树
这样的边界需要进行大量属性测试,预测时间开销大。为使边界划分不为于作标轴平行的线段设定非叶结点为属性的线性组合,形如 ∑ i = 1 d w i a i = t \sum_{i=1}^{d}w_ia_i=t ∑i=1dwiai=t的线性分类器,训练结果如下所示