基于MATLAB的离散系统的数字PID控制仿真

  第一次写博客，拿去年的课设试试手，仅供参考，不喜勿喷。

1 设计要求

控制对象为：
$$G(s)=\frac{523500}{s^3+87.35s^2+10470s}$$
  采样时间为1ms,针对离散系统的三角波信号、锯齿波信号和正弦波信号的位置响应，设计离散的增量式PID控制器。其中S为信号选择变量，S=1时为三角波跟踪，S=2时为锯齿波跟踪，S=3时为正弦波跟踪。对控制器的输出进行限幅：[-10，10]。
利用MATLAB 软件编写成可视化窗口实现如下功能：
（1） 针对离散系统的三角波信号、锯齿波信号和正弦波信号的位置响应，设计离散的增量式PID 控制器。
（2） 可视化窗口实现由键盘输入任意系统的传递函数、可选择三种输入信号的类型以及画出输入信号曲线与离散化后的输出曲线等功能。

---

直接来最终效果图如下：

---

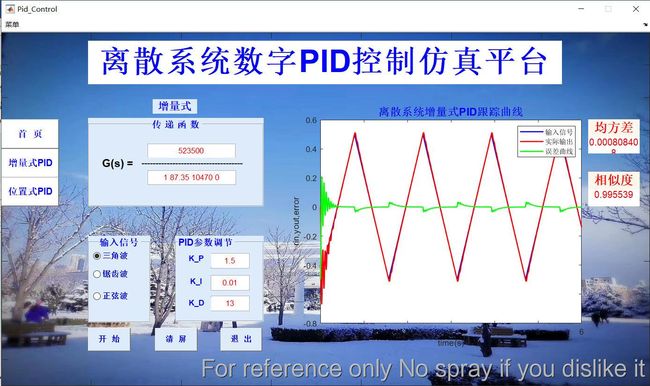
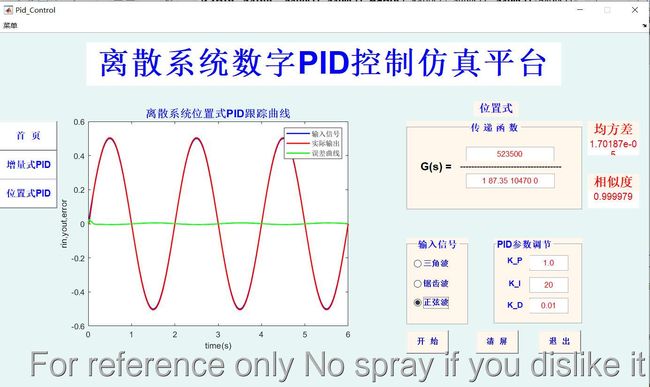
2 方案设计

2.1 设计思路及总体方案框图

  根据课题要求，可将可视化窗口分为以下两个部分实现：
（1）离散增量式PID 控制器的设计以及MATLAB 语言实现其仿真；
（2）可视化窗口的设计
总体方案框图如下图所示：

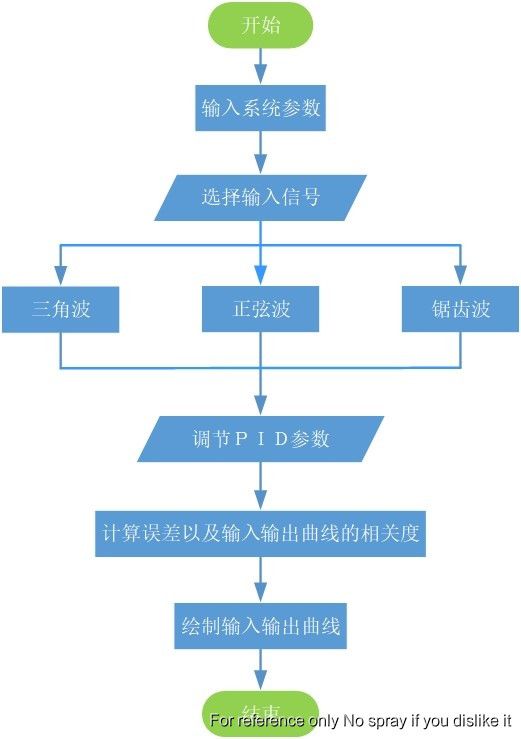
2.2 PID算法的基本原理

  常规PID控制器系统原理图如下图所示，这是一个典型的单位负反馈控制系统。系统由PID控制器和被控对象组成。

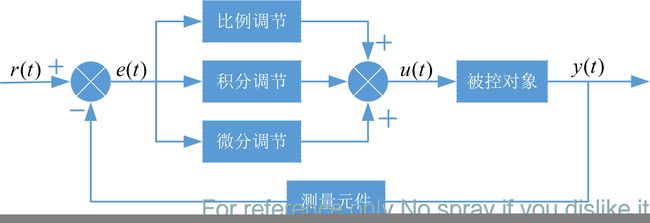
  PID控制器是一种线性控制器，它根据给定输入值r(t)与实际输出值y(t)构成偏差：e(t)=r(t)-y(t)。将偏差的比例P、积分I和微分D通过线性组合构成控制量，对受控对象进行控制。其控制规律为：
$$\mathrm{u}(t)=K_p[e(t)+\frac{1}{T_i}{\int }_0^{t}e(t)dt+T_d\frac{de(t)}{dt}]=K_{p}e(t)+K_i{\int }_0^{t}e(t)dt+K_d\frac{de(t)}{dt}$$
  上式中 $K_p$为比例系数， $T_i$为积分时间常数， $T_d$为微分时间常数;$K_i=\frac{K_p}{T_i}$为积分系数，$K_d=K_p\ast T_d$为微分系数，$\mathrm{u}(t)$ 为控制器的输出，$e(t)$为控制器的输入。

2.3 PID算法的离散化

  由课设题目知，系统的采样周期为$T=1ms$，设系统进行第k次采样时刻,控制器的输出值为：$u(k)$ 此时的偏差可以表示为:e(k)=r(k)-y(k),那么积分就可以表示为：$e(k)+e(k+1)+....$ ；而微分可以表示为:$(e(k)-e(k-1))/T$，于是，第k次采样时，PID算法的离散形式表示为：$$u(k)=K_{p}e(k)+K_i\sum e(k)+K_d(e(k)-e(k-1))$$
  则第k个采样周期的增量为:$\Delta u(k)=u(k)-u(k-1)$ ，根据式⑵与式⑶可知增量型PID算法的公式为：
$$\Delta u(k)=K_p(e(k)-e(k-1))+K_{i}e(k)+K_d(e(k)-2e(k-1)+e(k-2))$$
  因此，增量式PID控制器的输出为：
$$u(k)=\Delta u(k)+u(k-1)$$

3 总体方案的选择与设计

3.1 增量式PID控制器的基本实现

  增量式PID是指数字控制器的输出只是控制量的增量$\Delta u(k)$。采用增量式PID算法时，计算输出的控制量$\Delta u(k)$ 对应的是本次执行机构位置的增量，而不是执行机构得到实际位置，因此要求执行机构必须具有对控制量的累积功能，才能完成对被控对象的控制操作。执行机构的累积功能，才能完成对被控对象的控制操作。执行机构的累积功能可以采用硬件方法实现，也可以采用软件方法实现。
  下面是离散增量式PID的MATLAB算法实现

%增量式PID调用程序
%增量式PID就是本次PID输出与上次PID输出的差值
%u（k）-u(k-1)=kp*(e(k)-e(k-1))+ki*e(k)+kd*(e(k-1)-2*e(k-1)+e(k-2))
function [out1,correlation_coefficien1]= PIDcontrol1(S,kp1,ki1,kd1,nums,dens)
ts = 0.001;                         %采样时间
sys = tf(nums,dens);                %使系统系数可变
dsys = c2d(sys,ts,'z');             %将采样系统z变换进行离散化
[num,den] = tfdata(dsys,'v');       %获取离散后的分子分母系数矩阵

x = [0,0,0]';                       %将初始的P I D参数相乘的系数设置为0,x(1)=e(k)-e(k-1),x(2)=e(k),x(3)=e(k-1)-2*e(k-1)+e(k-2)
m = length(den);                    %计算矩阵的长度，获得输入的系统的阶次
out1 = 0;                           %原始误差为0
for i = 1:m-1                       %适用于不同阶次的系统，阶次=向量长度-常数项
    u_(i) = 0;
    y(i) = 0;              
end
error_last = 0;          
error_last_befor = 0;                       %迭代的6个参数初始值
for k = 1:1:6000;           %采样次数
    time(k) = k*ts;         %采样时刻
%-------------设置跟踪的函数-----------------%
     if        S == 1               %三角波
            r(k) = 0.5*sawtooth(2*2*ts*k,0.5);
        elseif S == 2           %锯齿波
            r(k) = 0.5*sawtooth(1.5*2*ts*k); 
        elseif S == 3           %正弦波信号
            r(k) = 0.5*sin(pi*k*ts);
     end
    
du(k) = kp1*x(1)+ki1*x(2)+kd1*x(3);   %控制控制器输出增量，根据离散PID表达式
u(k) = u_(1)+du(k);         
%限幅
    if u(k) >= 10
          u(k) = 10;
    end
    if u(k) <= -10
          u(k) = -10;
    end
yout(k) = 0;    %实际输出初始值
    for j = 2:1:m   %适用不同阶次的系统
        yout(k) = yout(k)-den(j)*y(j-1)+num(j)*u_(j-1);%实际输出值，通过脉冲传递函数转化为差分方程得到
    end

error(k) = r(k)-yout(k);             %误差等于期望减去实际

for i = m-1:-1:2
    u_(i) = u_(i-1);  % 保存上上次输入，为下次计算
    y(i) = y(i-1);    % 保存上上次输出，为下次计算
end
u_(1) = u(k);         % 保存上次输入，为下次计算 
y(1) = yout(k);       %保存上次输出，为下次计算
% kp,ki,kd系数
x(1) = error(k)-error_last;               
x(2) = error(k);
x(3) = error(k)-2*error_last+error_last_befor; 
%  参数更新
error_last_befor = error_last;
error_last = error(k);                    %误差在参数之间的传递
out1 = out1+error(k)^2;                  %误差的积累  平方和
end
out1 = out1/6000;    %  输出
correlation_coefficien1 = corr2(r,yout);
plot(time,r,'b',time,yout,'r',time,error,'g','linewidth',1.5);
zoom on;
xlabel('time(s)'),ylabel('rin,yout,error');         %横轴为时间，纵轴为输入输出
legend('输入信号','实际输出','误差曲线');
title(['\fontsize{14}\color{blue}离散系统增量式PID跟踪曲线'])

3.2 基于MATLAB的GUI界面的基本实现

  MATLAB GUI 为图形用户界面（Graphical User Interface，简称 GUI，又称图形用户接口）是指采用图形方式显示的计算机操作用户界面，是MATLAB用户可视化交互式的工具，运用GUI生成的操作界面用户可以不用浏览繁冗的代码而进行操作。
  在MATLAB软件的Command Window命令框中输入guide(必须是小写)并回车后即可进入GUI编辑界面。下图为此次课程设计的GUI编辑窗口：

  在编辑窗口内，界面顶部分别为菜单栏与工具栏（布局编辑器、对齐工具、对象属性观察器、菜单编辑器），界面左边是创建GUI时常用的控件，主要有：静态文本、编辑框控件、列表框控件、按钮控件、单选按钮控件等。每一个控件都有自己相应的属性，在GUI编辑界面内双击控件即可弹出控件的属性编辑对话框；每个控件都有几种回调函数，其中CallBack为一般回调函数，用户在GUI编辑界面右击控件并在弹出菜单框中点击View CallBacks选项即可找到相应的回调函数并自动定位到GUI界面的m文件中。
  此次课程设计的GUI界面主要用到了如下控件：按钮（Push Button）、单选按钮（Radio Button）、面板（Panel）、坐标轴（Axes）、按钮组（Button Group）、静态文本（Static Text）、编辑框（Edit Text）。GUI界面可实现的功能有：首页、增量式PID和位置PID三种界面间的切换、不同阶数的系统参数输入及PID参数的调节、输入输出曲线的绘制及保存、输出曲线与输入曲线之间的均方差比较以及相似度、界面背景（通过文件及选择图片）与颜色的设置等。

4 GUI各种功能的实现

4.1 任意离散系统的数字PID仿真

  根据课设题目要求，此次设计的GUI界面可实现题目的要求并能够通过界面切换实现增量式与位置式两种PID算法的仿真，下面主要分析增量式PID界面的实现，下图为增量式PID仿真的GUI界面：

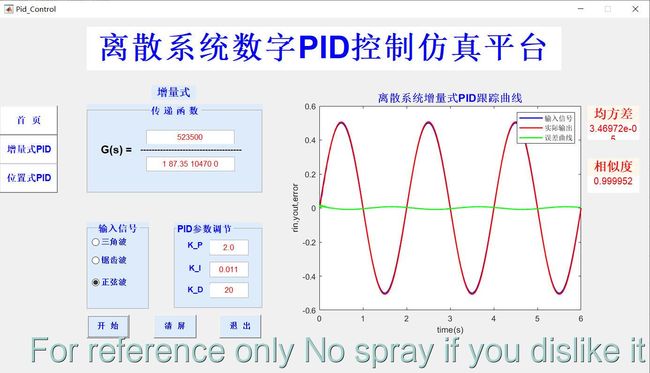
   此界面中传递函数参数输入、输入信号选择、PID参数调节均写在Button Group的SelectionChangedFcn回调函数中（见附录），当传递函数输入错误（输入中含有字符串、输入分子或分母为0等情况）会弹出“输入错误提示框”。
   错误提示框是MATLAB GUI常用的对话框之一，利用的是MATLAB中的创建错误对话框errordlg()函数，而errordl()函数常见的属于参数有四种形式，其区别是输入的参数四者不同，本次课程设计中输入三个参数，分别是对话框标题、对话框内容以及对话框设置。通过在查阅MATLAB文档知errordl()的第三个参数是对话框设置属性，可选项有’non-modal’，’modal’，’replace’三种，此次课程设计是将错误对话框指定为模态错误对话框。
   其中’non-modal’是创建一个非模态错误对话框，此对话框不影响其他打开的对话框；’modal’是指定模态错误对话框，如果其他错误对话框具有相同的标题，MATLAB 将用当前设定修改最近激活的错误对话框。MATLAB 将删除与最近激活的错误对话框具有相同标题的其他所有打开的错误、消息和警告对话框。受影响的对话框可以是模态对话框，也可以是非模态对话框。’replace’是指定为非模态错误对话框。此外，常见GUI中常用的对话框还有普通对话框（dialog）、警告对话框（warndlg）、帮助对话框（helpdlg）、信息对话框（msgbx）、提问对话框（questdlg）等。
   下面是参数的输入与错误提示框的应用代码实现：

%--------------------------增量式--------------------------%
% --- Executes when selected object is changed in options1.
function options1_SelectionChangedFcn(hObject, eventdata, handles)
% hObject    handle to the selected object in options1 
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
Kp1 = 0;
Ki1 = 0;
Kd1 = 0;
nums1 = 0;
dens1 = 0;
%-----------------输入参数---------------------%
Kp1 = str2double(get(handles.K_P1,'String'));
Ki1 = str2double(get(handles.K_I1,'String'));
Kd1 = str2double(get(handles.K_D1,'String'));
nums1 = str2num(get(handles.nums1,'String'));
dens1 = str2num(get(handles.dens1,'String'));

% ----------------判断输入参数-----------------%
  % --------判断是否全为0-----------%
nums1_q1 = any(nums1);  % 判断是否全为0
dens1_q1 = any(dens1); 
Kp1_q1 = any(Kp1);
Ki1_q1 = any(Ki1);
Kd1_q1 = any(Kd1);

nums1_s1 = length(nums1);  % 判断是否为空
dens1_s1 = length(dens1); 

  if Kp1_q1 == 0 
      Kp1 = 0; 
  end
  if Ki1_q1 == 0 
      Ki1 = 0; 
  end
  
  if Kd1_q1 == 0 
      Kd1 = 0; 
  end

 if    nums1_q1 == 0 || dens1_q1 == 0 || nums1_s1 == 0 || dens1_s1 == 0
     errordlg('请输入系统正确的参数','错误(Error)！','modal');
     set(handles.nums1,'String',' ');  %  输错后清空文本框
     set(handles.dens1,'String',' ');
 else
        q_1 = get(handles.Sanjiaobo_2,'Value');
        q_2 = get(handles.Juchibo_2,'Value');
        q_3 = get(handles.Zhengxianbo_2,'Value');
      axes(handles.axes1); 
           if q_1 == 1 
                [out1, correlation_coefficien1]= PIDcontrol1(1,Kp1,Ki1,Kd1,nums1,dens1);
           elseif q_2 == 1
                [out1, correlation_coefficien1] = PIDcontrol1(2,Kp1,Ki1,Kd1,nums1,dens1);
           elseif q_3 == 1
                [out1, correlation_coefficien1] = PIDcontrol1(3,Kp1,Ki1,Kd1,nums1,dens1);   
           end
   set(handles.error_txt1,'String',out1)
   set(handles.xishu,'String',correlation_coefficien1);
 end

4.2 曲线保存功能的实现

  为使得设计的GUI更加方便用户的使用，在设计的GUI界面顶部菜单栏（Menu Editor）的选项框中增加了输入输出曲线的保存选项（保存增量式PID曲线、保存位置式PID曲线），用于保存仿真产生的主要是利用MATLAB软件中的copyobj()函数将当前坐标轴中的内容复制到新创建的figure中，利用uiputfile()函数打开保存路径提示框选择相应的路径保存即可,而保存曲线所用的函数是常见的print()函数，即把新创建的figure保存在uiputfile()函数返回的路径中。最后通过返回的fileindex值来判断是否保存成功（fileindex值为0，则鼠标点击取消选项框，即未保存，反之，则保存成功），并通过帮助对话框(helpdlg)来产生保存成功对话框，方便用户的使用。
  下面是曲线保存的代码实现：

% -------------------保存增量式PID曲线---------------------%
function Increased_plot_Callback(hObject, eventdata, handles)   
% hObject    handle to Increased_plot (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
new_f_handle = figure('visible','off');
new_axes = copyobj(handles.axes1,new_f_handle); %axes1是GUI界面绘图的坐标系句柄
set(new_axes,'units','default','position','default');
legend('Parent',new_f_handle,'String',{'输入曲线','实际输出','误差曲线'});%让输出保存的曲线带有坐标轴
[filename,pathname,fileindex]=uiputfile({'*.jpg';'*.bmp'},'save picture as');
if ~filename
     return
else
      file = strcat(pathname,filename);
      switch fileindex %根据不同的选择保存为不同的类型
      case 1
                  print(new_f_handle,'-djpeg',file);
      case 2
                  print(new_f_handle,'-dbmp',file);
      end
    if fileindex   
        %保存成功对话框
         helpdlg('保存成功','提示');
    end
end
delete(new_f_handle);

4.3 界面背景的设计

  在菜单栏中增加了整个GUI界面的背景更改功能，包括系统自带的纯色背景颜色设置以及用户自定义的图片背景设置。
代码如下：

 -------------------通过文件路径设置桌面背景------------------%
function Background_Callback(hObject, eventdata, handles)
% hObject    handle to Background (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
%------------------设置背景--------------------%
    [filenm pathnm c] = uigetfile({'*.jpg';'*.bmp'},'选择背景图片');
    new_path = strcat(pathnm,filenm);
    ha1 = axes('Parent',gcf,'units','normalized','pos',[0 0 1 1]);
    uistack(ha1,'bottom');
    ii1 = imread(new_path);
    image(ii1);
    colormap gray
    set(ha1,'handlevisibility','off','visible','on');   %  没有这句话  会导致鼠标滚动  然后背景放大
    set(gcf,'WindowStyle','normal');                    %  哈哈哈哈 这样可以避免菜单栏被遮住
 %----------------------------------------------------%

% --------------------------------------------------------------------
function figure_Color_Callback(hObject, eventdata, handles)
% hObject    handle to figure_Color (see GCBO)
% eventdata  reserved - to be defined in a future version of MATLAB
% handles    structure with handles and user data (see GUIDATA)
c = uisetcolor;  %使用1  c 返回颜色值
set(gcf,'Color',c);

5 总结

  本次课程设计是对PID算法以及MATLAB应用的初步掌握，通过将近一周时间自学了MATLAB GUI的设计，对PID算法有了进一步的认识。期间遇到过许多上述提到过的类似问题，虽然这些问题看似简单，但如若不亲自经历并寻求方法解决，下次遇到可能仍然不会解决。此外，通过此次课程设计，我也明白了自学能力的重要性，在今后的学习中，我们仍会遇到各种难题，这些都需要我们通过自学逐渐解决。最后，课程设计的结果固然重要，但是我认为这个过程才是更重要的，过程中培养的能力、掌握的经验会让我们受益终身。