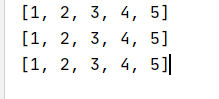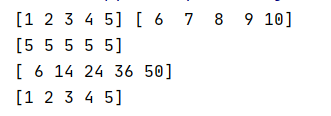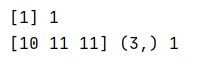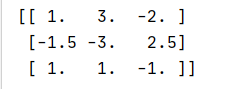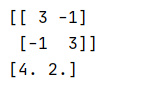机器学习-01-Numpy-01

                                                          前言

---

目录

                                                          前言

1.1机器学习是什么：

1.2学习资料

1.3为什么要学机器学习

2.1创建矩阵

2.1.1传入列表生成数组

2.2.2使用arange创建数组

2.2.3创建多维矩阵

2.3矩阵运算

2.3.1数学标量运算

2.3.2矩阵运算

2.4切片

---

1.1机器学习是什么：

说到机器学习，应该首先提到“人工智能”，人工智能，当然是模拟人的智慧，比如我们看小说，听说书，单纯的字符或者语音就能在脑海中形成一幅幅画像，又比如司机开车，清洁工扫地。人的活动总是有输入，如语音，图像，触觉，嗅觉，人通过这些信息的输入，来作出反应。机器学习是人工智能的一种实现方式，具体步骤是

1.数据的特征提取

2.数据预处理

3.训练模型

4.测试模型

5.模型评估

如果按我个人的理解，机器学习过程就是处理数据输入-得到模型-输出预测数据。这个模型的话，硬要举例，高中一元二次方程f(x)=ax^2+bx+c,利用输入数据，求出a b c 三个变量，得到的f(x)就是模型

1.2学习资料

机器学习有学习步骤，资料书籍很多，这些文章仅仅记录我的学习过程，如果读者想通过我的博客来学习机器学习，恐怕会失望，自行搜索相关资料去学习

当然我也是和大家一样，零基础，共同学习吧。看博客的好处就是，至少我写的毕竟浅显，不容易放弃

1.3为什么要学机器学习

说实话，没什么用，也帮助不了你找工作，甚至还被挂上一个"看的东西太杂，泛而不精"的牌子，就像我们学英语，学了10年，靠英语专业找到工作的人毕竟是少数，但是不能说英语没有用，找不到英语有关的工作，就说我10年英语白学了，是不正确的说法。所有要端正态度，解放思想，不说机器学习，本科阶段的算法，计网，组员，操作系统。你说我不搞网络，也不设计芯片，也不去微软写操作系统，就白学了?就是一个工具，学习的目的在于增长见识，至少别人说一个现象，得知道书本上是哪个名词吧。总结下，学习机器学习，不能让你的思想境界变得更高，也不能增加你的薪水，不能改善你的工作环境，在你打英雄联盟刷抖音的时候，你甚至不能改变它的匹配和推送。我期望学完了机器学习和深度学习，就像能自动玩flappy birdy一样，能做一个坦克大战小游戏AI，就很不错了。（虽然不知道深度学习能否实现这个操作）。废话不多说，先从矩阵库Numpy开始学习吧。

话说我爬虫和图形学的坑也还没填，又开新坑，我保证再不开坑了。

另外不怕遗忘，至少学完了，你能知道机器学习能干什么，不能干什么，这已经超过一大截把“机器学习”挂在嘴边的程序员了

其实我觉得写代码或者看书都不能让我快乐，而写文章能让我很快乐，难道我真的不适合程序员？

---

2.1创建矩阵

前置知识：https://blog.csdn.net/qq_34153210/article/details/107580000

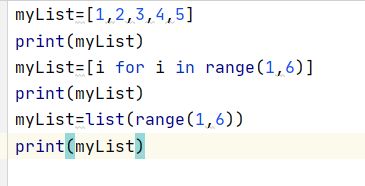
我们用python可以创建list,如下

我们甚至可以创建一个二维数组

 现在我们来创建一个矩阵试试

2.1.1传入列表生成数组

import numpy as np
myLists=[]
for i in range(1,26,5):
    myList=[]
    for j in range(5):
        myList.append(i+j)
    myLists.append(myList)
myMatrix=np.array(myLists)
print(myMatrix)

看上去也没有什么不一样吗，无非是一行变成了5行，每行的逗号都去掉了

我们访问一下中间的值13

import numpy as np
myLists=[]
for i in range(1,26,5):
    myList=[]
    for j in range(5):
        myList.append(i+j)
    myLists.append(myList)
myMatrix=np.array(myLists)
print(myLists[2][2])
print(myMatrix[2][2])

甚至一样能用for循环

2.2.2使用arange创建数组

就像用range创建列表一样，使用arrange也可以创建矩阵，但是只是一维矩阵

import  numpy as np
myMatrix=np.arange(1,26)
print(myMatrix)

直观的看，矩阵和列表的区别就是没有逗号，我们现在将一维矩阵改变一下形状

import  numpy as np
myMatrix=np.arange(1,26)
newMatrix=myMatrix.reshape(5,5)
print(newMatrix)

列表里的每一个数据，可以是字符，数字，甚至对象

但是矩阵不一样，矩阵是用来做数学计算的，只能是数字，数字的类型有整数，浮点数

虽然numpy也支持矩阵的值为 对象，布尔值，字符串

我们可以修改矩阵的数据类型，并打印其数据类型

import  numpy as np
myMatrix=np.arange(1,26)
newMatrix=myMatrix.reshape(5,5)
print("newMatrix的数据类型是：",newMatrix.dtype)
m1=newMatrix.astype(np.float64)
print(m1)
m2=newMatrix.astype(np.string_)
print(m2)
m3=newMatrix.astype(np.bool)
print(m3)

2.2.3创建多维矩阵

如果说前面的array,arange方法过于繁琐，我们可以使用下面的方法，创建矩阵

import numpy as np
#使用zero创建全0矩阵
m1=np.zeros((5,5))
print(m1)
#指定数据类型
m2=np.zeros((5,5),dtype=np.int)
print(m2)
#使用ones创建全1矩阵
m3=np.ones((5,5))
print(m3)
print("m3矩阵维度：",m3.ndim)
print("m3矩阵形状：",m3.shape)#区别于reshape改变形状

2.3矩阵运算

2.3.1数学标量运算

同样维度的矩阵与矩阵的运算结果是每一个矩阵的对应元素进行加减乘除（不同于矩阵的内积，向量积）

感觉离开大学了，人学习能力发生了退化，悲哉

矩阵与标量的运行结果，就是矩阵每一个元素与标量进行运算

看下面的两个例子

import numpy as np
m1=np.arange(1,6)#左开右闭
m2=np.arange(6,11)
print(m1,m2)
print(m2-m1)#矩阵和矩阵减法
print(m1*m2)#矩阵和矩阵乘法
print(m2-5)#矩阵减去一个标量

那如果数据维度不一样，两个矩阵相加的时候，低维度会自动向高纬度扩维，如下

import numpy as np
m=np.array([1])
print(m,m.ndim)
n=np.array([9,10,10])
p=m+n
print(p,p.shape,p.ndim)

2.3.2矩阵运算

学线性代数的时候，接触到了矩阵转置，求逆矩阵，求矩阵的点乘叉乘，求矩阵的特征值特征向量，甚至求的方程组的基础解系

这些numpy都能帮我们实现

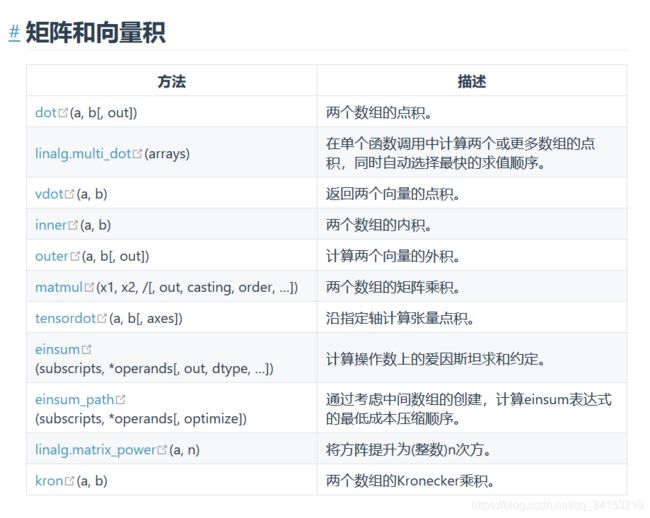
来源：https://www.numpy.org.cn/reference/routines/linalg.html#%E8%8C%83%E6%95%B0%E5%92%8C%E5%85%B6%E4%BB%96%E6%95%B0%E5%AD%97

太多了，所以我们就挑几个讲讲把

（1）转置矩阵

import numpy as np
m=np.arange(1,10).reshape(3,3)
print("m矩阵为：\n",m)
print("m转置矩阵为：\n",m.T)
print("m另一种转置方法为：\n",m.transpose(1,0))

（2）逆矩阵

import numpy.linalg as npl
import numpy as np
m=np.array([[1,2,3],[2,2,1],[3,4,3]],dtype=np.int)
n=npl.inv(m)
print(n)

后面我们用内积验证一下这个逆矩阵求的对不对，现在我们先看教科书的答案

（3）内积

import numpy as np
m=np.array([1,1,1])
n=np.array([1,-2,1])
p=np.inner(m,n)
print(p)

（4）外积

略

（5）特征值

import numpy as np
m=np.array([[3,-1],[-1,3]],dtype=np.int)
print(m)
f=np.linalg.eigvals(m)
print(f)

我们看看特征值是不是[4,2]

（6）奇异值分解

这个搜到了一个好玩的东西，有机会补上这个奇异值分解的应用。这里先跳过

前后花了4天，差不多肝出来了，奇异值分解的应用

奇异值分解的定义及应用

2.4索引和切片

2.4.1一般索引

列表的索引

a1=[1,2,3]
print(a1[0:1])

索引规则是左开右闭

同样一个二维矩阵，我要获取某一行某一列，如下

import numpy as np
a=np.arange(1,10)
a=a.reshape((3,3))
print(a)
#输出第一行
print(a[0,:])
#输出第一列
print(a[:,0])
#输出23行23列
print(a[1:3,1:3])

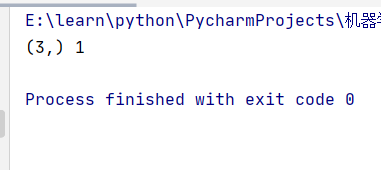
拿截取某一列举例，取列向量后，变成了一维矩阵

import numpy as np
a=np.arange(1,10)
a=a.reshape((3,3))
#输出第一列
print(a[:,0].shape,a[:,0].ndim)

有没有办法使之成为三行一列二维矩阵

import numpy as np
a=np.arange(1,10)
a=a.reshape((3,3))
a1=a[:,0]
a1= np.expand_dims(a1, axis=1)
print(a1)
print(a1.shape)

2.4.2布尔索引

import numpy as np
a=np.arange(1,10)
a=a.reshape((3,3))
s=[True,False,False]
print(a[s])

同样我们可以截取第一列

import numpy as np
a=np.arange(1,10)
a=a.reshape((3,3))
s=np.array([[True,False,False],[True,False,False],[True,False,False]])
print(a[s])

布尔值能作为索引，比如[True,False,False],等价于[0:1]

2.4.3花式索引

花式索引传值，而不是传址

import numpy as np
a=np.arange(1,10).reshape((3,3)).astype(np.int)
print(a[[2,1,0]])

索引中的数组[2,1,0]相当于调换了矩阵第一维的顺序，

0->2,1->1,2->0

所以截取第一列还可以这样写

import numpy as np
a=np.arange(1,10).reshape((3,3)).astype(np.int)
print(a[[0,1,2],[0,0,0]])

2.5函数

我们可以对矩阵每一个元素进行操作，比如平方

import numpy as np
a=np.arange(1,10).reshape((3,3)).astype(np.int)
print(a**2)

当然我们也可以使用np函数

import numpy as np
a=np.arange(1,10).reshape((3,3)).astype(np.int)
print(np.square(a))

np.square是一个一元函数，当然也有二元函数，支持传入两个矩阵

import numpy as np
a=np.arange(1,10).reshape((3,3)).astype(np.int)
b=np.arange(1,10).reshape((3,3)).astype(np.int)
print(np.multiply(a,b))

这三段代码作用一样

更多函数的内容请参见

https://www.numpy.org.cn/reference/ufuncs.html#%E6%95%B0%E5%AD%A6%E8%BF%90%E7%AE%97

2.6数据处理

待续