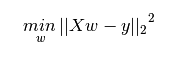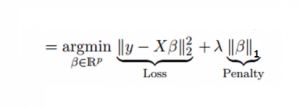机器学习入门之7种经典回归模型
介绍
线性和逻辑回归通常是学习数据科学时接触的第一个算法,由于它们非常流行,许多分析师甚至认为它们是唯一的回归技术。
事实上,存在多种不同形式的回归模型,每种形式都有自身的特点和特定的应用场景。在本文中,我将简要介绍数据科学中最常用的7种回归模型。
通过本文,我希望人们对回归分析有更深入的理解,而不是仅仅停留在线性回归和逻辑回归的层面。
本文来自《数据黑客》,登录官网可阅读更多精彩资讯和文章。
目录
- 什么是回归分析?
- 为什么使用回归分析?
- 有哪些常用的回归模型?
- 线性回归
- 逻辑回归
- 多项式回归
- 逐步回归
- Ridge回归
- Lasso回归
- ElasticNet回归
- 如何选择正确的模型?
1. 什么是回归分析?
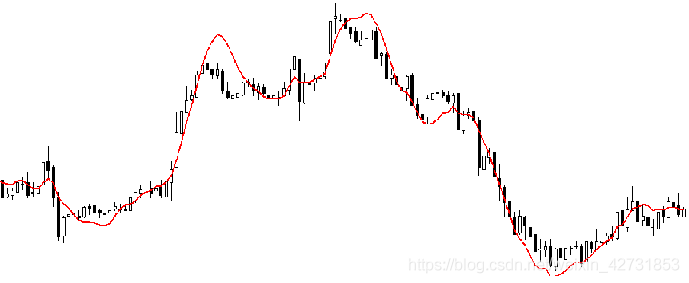
回归分析是一种预测建模技术,用于研究因变量(目标变量)与自变量(预测变量/特征)之间的关系。该技术用于预测,时间序列建模以及检验变量之间的因果关系。例如,通过回归分析研究疲劳驾驶与道路交通事故发生次数之间的关系。
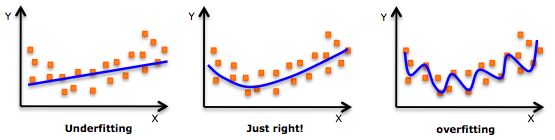
回归分析是建模和分析数据的重要工具。如上图所示,我们尝试用曲线拟合数据点,以使数据点到曲线的距离之和最小化。我将在接下来的部分详细说明这一点。
2. 为什么要使用回归分析?
如上所述,回归分析估计两个或多个变量之间的关系。让我们举一个更简单的例子:
假设您要根据当前的经济状况估算公司的销售增长,您具有最新的公司数据,该数据表明销售增长约为经济增长的两倍半。利用这一见解,我们可以根据当前和过去的信息来预测公司未来的销售。
使用回归分析有多个好处,比如:
- 评估因变量和自变量之间是否显著相关。
- 评估多个自变量对因变量的影响强度。
回归分析还能够比较在不同规模上测量的变量的关系,例如价格变化对促销商品数量的影响。这些好处可帮助市场研究人员/数据分析师/数据科学家创建用于预测的最佳变量集。
3. 有哪几种类型的回归模型?
有多种回归模型可用于预测,这些技术主要由三个指标(自变量数量,因变量类型和回归线的形状)驱动。我们将在以下各节中详细讨论它们。
4. 线性回归
线性回归是最广为人知的建模技术之一,它通常是学习机器学习时最先接触的技术。在线性回归中,因变量是连续的,自变量可以是连续的或离散的,并且模型相对于系数也是线性的。
线性回归使用最佳拟合直线(回归线)在因变量(Y)和一个或多个自变量(X)之间建立关系。它由等式Y = a + b * X + e表示 ,其中a是截距系数,b是斜率系数,e是误差项。
简单线性回归和多元线性回归的区别在于,多元线性回归有多个自变量,而简单线性回归只有1个自变量。现在,问题是“如何获得最佳拟合线?”。
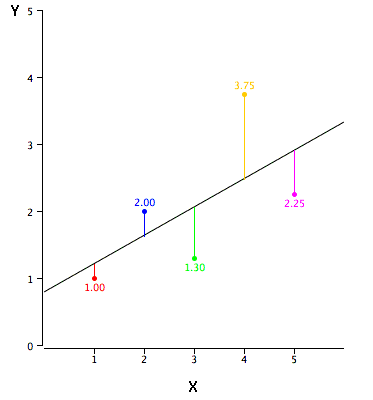
如何获得最佳拟合线?
获得回归线的最常用方法是最小二乘估计(OLS),它通过最小化每个数据点到拟合线的垂直偏差的平方和来估计回归系数。由于使用偏差的平方,所以相加时就不会抵消正值和负值的差异。
我们可以使用R平方(可决系数)来评估模型性能。要了解这些指标的详细信息,请阅读:模型性能指标:第一部分,第二部分。
评论:
- 自变量和因变量之间必须存在线性关系。
- 多元回归模型会受到多重共线性,自相关,异方差性的影响。
- 线性回归对离群值非常敏感,它会严重影响回归模型的预测精度。
- 多重共线性会增加系数估计的方差,并使估计系数对模型的微小变化非常敏感。
- 如果有多个自变量,可以使用正向选择,向后消除和逐步回归来挑选最重要的自变量。
5. 逻辑回归
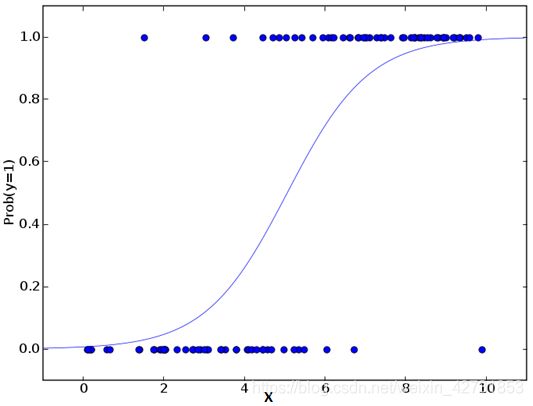
逻辑回归(Logistic Regression)用于评估事件成功或失败的概率。当因变量是二元分类变量(如0或1,True或False,Yes或No)时,可以使用逻辑回归。一般用以下公式表示逻辑回归方程,其中p是感兴趣的事件发生的概率:
odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence
ln(odds) = ln(p/(1-p))
logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
为什么使用对数?由于假定因变量服从二项分布,我们需要选择最适合此分布的链接函数(即logit函数)。
评论:
- 逻辑回归广泛应用于分类问题。
- 逻辑回归不要求因变量和自变量具有线性关系。
- 为避免过度拟合和拟合不足,我们应包括所有重要变量,最佳实践是利用逐步回归技巧。
- 样本要足够大,最大似然估计在小样本上的估计精度较低。
- 自变量要求相互独立,即无多重共线性。但是,选择函数形式时可以包括类别变量的交互作用。
- 如果因变量的值是序数,称为序数逻辑回归。
- 如果因变量包含多个类别,称为多元逻辑回归。
6. 多项式回归
如果自变量的幂大于1,就是多项式回归,如以下方程所示:
y=a+b*x^2
多项式回归的拟合曲线是非线性的:
评论:
- 虽然可以使用更高阶的多项式以获得较低的误差,但是会导致拟合过度。可视化回归线和观测值的关系可以帮助判断是过度拟合还是拟合不足,如下图:
- 尤其要注意末端的曲线,观察它的形状和趋势是否有意义。
7. 逐步回归
当数据集有很多自变量时,可以使用逐步回归。逐步回归与其说是一种回归模型,倒不如说是拟合最佳模型的一种技巧。这种技术的目标是自动选择最佳的自变量,无需人工干预。
逐步回归通过评估R-square,t统计量或AIC(赤池信息准则)的变化来确定是否往模型中添加一个变量(或剔除一个变量)。有三种常见形式:
- 向前向后逐步回归,每次迭代都往模型添加和删除预测变量。
- 向前逐步回归,模型从最重要的预测变量开始,每次迭代往模型中添加变量。
- 向后逐步回归,初始模型会包含所有预测变量,每次迭代剔除无预测意义的变量。
8. 岭回归
岭回归(Ridge Regression)是一种当自变量存在多重共线性时使用的技术。在多重共线性中,即使最小二乘估计(OLS)是无偏的,系数估计值的误差也很大。普通最小二乘估计的目标是最小化残差平方和,岭回归在目标函数中添加惩罚项,对估计系数做出限制,如下式:
目标函数包含两个部分,左边部分是残差平方和,右边是惩罚项,其中β是系数,lambda是惩罚因子,lambda越大惩罚力度越大,估计系数的取值就越小。
评论:
- 岭回归的假设与普通线性回归相同,但不要求正态性。
- 岭回归会缩小系数的值,但不会达到零。
- 这是一种正则化方法,称为L2正则化。
9. 罗素回归
与岭回归相似,罗素回归(Lasso Regression)也惩罚了回归系数的绝对大小。此外,它能够减少变异性并提高回归模型的准确性。上述方程显示了罗素回归和岭回归的不同之处,前者在惩罚项中使用绝对值而不是平方,这导致某些参数估计值恰好为零。施加的惩罚越大,则估计值进一步缩水至零,进而实现特征选择。
评论:
- 罗素回归的假设与简单线性回归相同,但不假定正态性。
- 罗素回归可以将系数估计值缩小为零,有助于特征选择。
- 罗素回归是一种正则化方法,称为L1正则化。
- 如果一组预测变量高度相关,Lasso只会选择其中一个并将其他变量的系数缩小为零。
10. ElasticNet回归
ElasticNet是Lasso和Ridge回归技术的混合,事先用L1和L2正则化。当存在多个高度相关的特征时,Elastic-net非常有用。它的目标函数如下式:
![]()
评论:
- 当特征高度相关时,ElasticNet会鼓励组内效应。
- 所选变量的数量没有限制。
- 它可能会遭受双重收缩。
除了这7种最常用的回归技术之外,您还可以查看其他模型,比如:贝叶斯回归,生态回归和稳健回归。
11. 如何选择正确的回归模型?
当只掌握一种或两种技术时,很容易做出选择,但是当可用模型的选择很多时,很难做出正确的决定。
在选择回归模型时,重要的考量因素包括:自变量和因变量的类型,数据的维数以及其他基本特征。以下是一些经验法则:
- 创建模型前先探索数据,确定变量间的关系。
- 利用不同的指标来评估模型的拟合优度,例如参数的统计显着性,可决系数,调整后可决系数,AIC,BIC和误差项。
- 交叉验证是评估模型预测精度的最佳方法,要把数据集划分为训练集和检验集。实际观测值和模型预测值之间的简单均方差可作为预测精度的度量指标。
- 如果数据集有多个混淆变量,则不应使用自动模型选择方法,一般不会同时将它们放在模型中。
- 明确需要什么样的模型,与具有高度统计意义的模型相比,功能较弱的模型易于实现。
- 正则化方法(Lasso,Ridge和ElasticNet)在高维数据集和存在多重共线性的情况下效果更好。
来源:AnalyticsVidhya
作者:SUNIL RAY
翻译校对:数据黑客
原文标题:7 Regression Techniques you should know!
数据黑客:专注金融大数据,聚合全网最好的资讯和教程,提供开源数据接口。
我们聚合全网最优秀的资讯和教程:
- 金融大数据
- 机器学习/深度学习
- 量化交易
- 数据工程
- 编程语言,Python,R,Julia,Scala,SQL
我们提供开源数据接口:
- 下载国内和国外海量金融数据
- API接口,将数据整合到您的平台