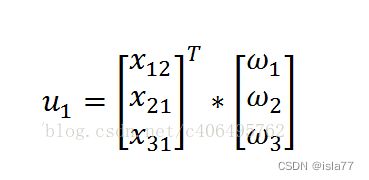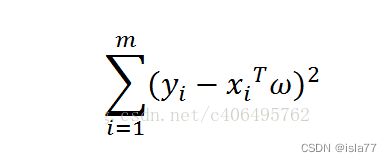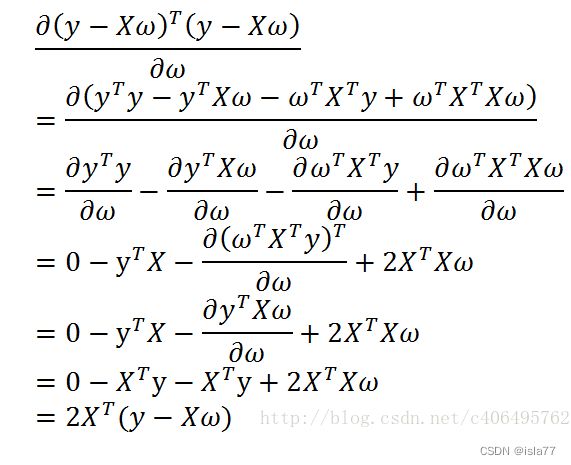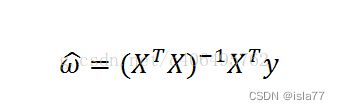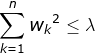《机器学习实战》学习笔记第八章-回归

目录

线性回归

标准回归

 局部加权线性回归

预测鲍鱼的年龄

 缩减系数来“理解”数据

岭回归

lasso

前向逐步回归

预测乐高玩具套件的价格

获取数据

---

线性回归

回归的目的就是预测数值型的目标值

最直接的方法是 依据输入写出一个目标值的计算公式

一般线性回归y=w*x+b，回归和线性回归一般是一个意思。

参考(2条消息) Python3《机器学习实战》学习笔记（十一）：线性回归基础篇之预测鲍鱼年龄_Jack-Cui的博客-CSDN博客

应该怎么从一大堆数据里求出回归方程呢？假定输入数据存放在矩阵X中，结果存放在向量y中，而回归系存放在向量w中：

 那么对于给定的数据x1，即矩阵X的第一列数据，预测结果u1将会通过如下公式给出：

 

现在的问题是，手里有数据矩阵X和对应的标签向量y，怎么才能找到w呢？一个常用的方法就是找出使误差最小的w。这里的误差是指预测u值和真实y值之间的差值，使用该误差的简单累加将使得正差值和负差值相互抵消，所以我们采用平方误差。

平方误差和可以写做：

 我们要找到w，使平方误差和最小。因为我们认为平方误差和越小，线性回归拟合效果越好。

因此，用平方误差和对w进行求导：

 使导数为0，得到

 

标准回归

数据导入

def loadDataSet(fileName):
    numFeat = len(open(fileName).readline().split('\t')) - 1
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr =[]
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

标准回归函数

def standRegres(xArr,yArr):#x数据集，y数据集
    xMat = np.mat(xArr); yMat = np.mat(yArr).T
    xTx = xMat.T * xMat #根据文中推导的公示计算回归系数 2*2矩阵
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵,不能求逆")
        return
    ws = xTx.I * (xMat.T*yMat)
    return ws  #回归系数

画图

xArr,yArr = loadDataSet('ex0.txt')
ws = standRegres(xArr,yArr)
xMat = np.mat(xArr)
yMat = np.mat(yArr) #真实y值
yHat = xMat*ws #用ws回归系数算出来的y值

xCopy = xMat.copy()                   
xCopy.sort(0)   #排序
yHat = xCopy * ws    #计算对应的y值
fig = plt.figure()
ax = fig.add_subplot(111)             
ax.plot(xCopy[:, 1], yHat) #绘制回归曲线
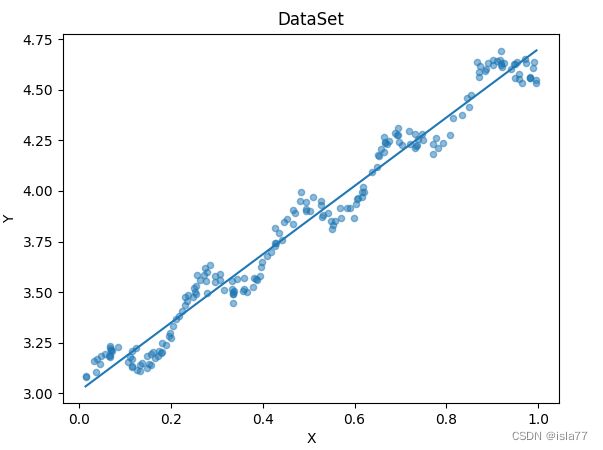
ax.scatter(xMat[:,1].flatten().A[0], yMat.flatten().A[0], s = 20, alpha = .5) #绘制样本点
plt.title('DataSet')                  
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

 如何判断模型的好坏呢？可以计算预测值yHat和真实值之间的相关系数

xArr,yArr = loadDataSet('ex0.txt')
ws = standRegres(xArr,yArr)
xMat = np.mat(xArr)
yMat = np.mat(yArr) #真实y值
yHat = xMat*ws #用ws回归系数算出来的y值
corr = np.corrcoef(yHat.T,yMat)
print(corr)

结果：相关系数为0.98

 局部加权线性回归

线性回归可能出现欠拟合的问题，因为它求的是具有最小均方误差的无偏估计。可以在估计中引入一些偏差，来降低预测的均方误差。比如局部加权线性回归（LWLR），给待测点附近的每个点赋予一定的权重，回归系数w解法：

LWLR 使用“核”（与支持向量机中的“核”类似）来对附近的点赋予更高的权重。核的类型可以自由选择，最常用的核就是高斯核，高斯核对应的权重如下，点x与x(i)越近，w(i,i)将会越大

 公式中唯一需要考虑的参数K，决定了对附近的点赋予多大的权重。k越小，表明越少的点被用于训练回归模型。

# 使用局部加权线性回归计算回归系数w
def lwlr(testPoint, xArr, yArr, k = 1.0):
    xMat = np.mat(xArr); yMat = np.mat(yArr).T
    m = np.shape(xMat)[0]
    weights = np.mat(np.eye((m)))#创建权重对角矩阵
    for j in range(m): #遍历数据集计算每个样本的权重
        diffMat = testPoint - xMat[j, :]                                 
        weights[j, j] = np.exp(diffMat * diffMat.T/(-2.0 * k**2)) #随着样本点与待测点距离的递增，权重将以指数级衰减
    xTx = xMat.T * (weights * xMat)                                        
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵,不能求逆")
        return
    ws = xTx.I * (xMat.T * (weights * yMat))  #计算权重回归系数
    return testPoint * ws
#为数据集中的每个点调用lwlr()
def lwlrTest(testArr, xArr, yArr, k=1.0):  
    m = np.shape(testArr)[0] #计算测试数据集大小
    yHat = np.zeros(m)    
    for i in range(m):  #对每个样本点进行预测
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat

xArr,yArr = loadDataSet('ex0.txt')
yHat = lwlrTest(xArr,xArr,yArr,1.0)
xMat = np.mat(xArr)
srtInd = xMat[:, 1].argsort(0)  #排序，返回索引值
xSort = xMat[srtInd][:,0,:]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(xSort[:, 1], yHat[srtInd])
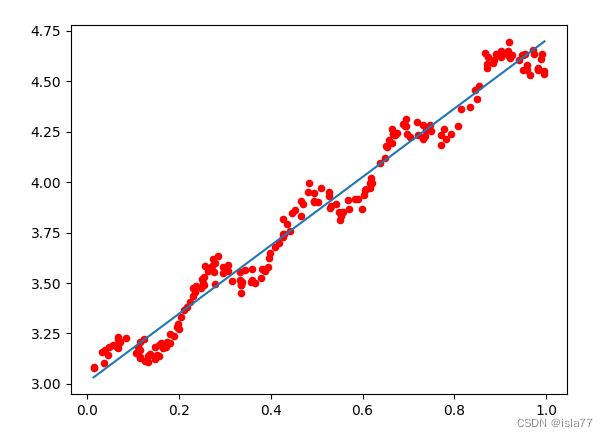
ax.scatter(xMat[:,1].flatten().A[0], np.mat(yArr).flatten().A[0], s = 20, c = 'red')
plt.show()

 k=1时

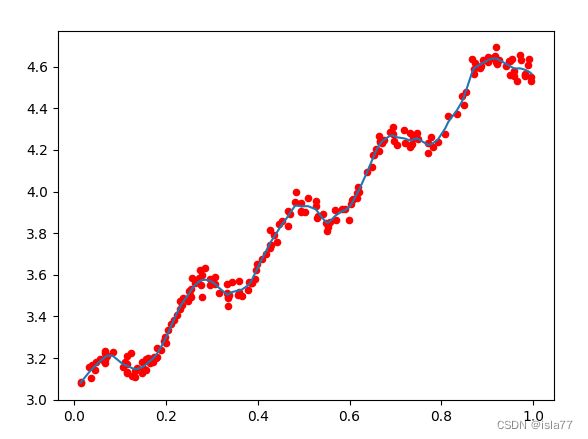
 k=0.01

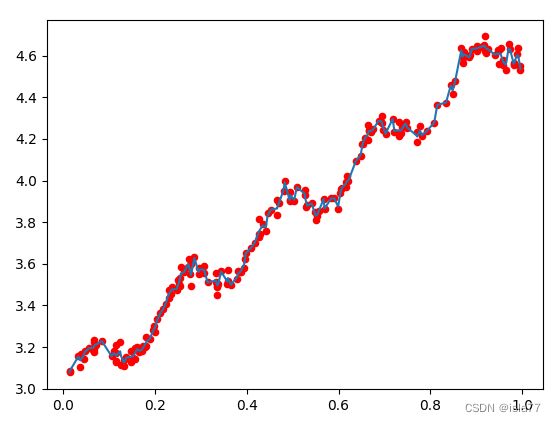
 k=0.003

可以看到，k = 1.0时的模型效果与最小二乘法差不多，k = 0.01时该模型可以挖出数据的潜在规律，而k = 0.003时则考虑了太多的噪声，进而导致了过拟合现象。

局部加权线性回归也存在一个问题，即增加了计算量，因为它对每个点做预测时都必须使用整个数据集。如果避免这些计算将可以减少程序运行时间，从而缓解因计算量增加带来的问题。

预测鲍鱼的年龄

计算误差

def rssError(yArr,yHatArr):
    return ((yArr-yHatArr)**2).sum()

不同的K:

abX,abY = loadDataSet('abalone.txt')
yHat01 = lwlrTest(abX[0:99],abX[0:99],abY[0:99],0.1)
yHat1 = lwlrTest(abX[0:99],abX[0:99],abY[0:99],1)
yHat10 = lwlrTest(abX[0:99],abX[0:99],abY[0:99],10)
print(rssError(abY[0:99],yHat01.T))
print(rssError(abY[0:99],yHat1.T))
print(rssError(abY[0:99],yHat10.T))

最小的核对应最低的误差

换数据集，不同的k：

abX,abY = loadDataSet('abalone.txt')
yHat01 = lwlrTest(abX[100:199],abX[0:99],abY[0:99],0.1)
yHat1 = lwlrTest(abX[100:199],abX[0:99],abY[0:99],1)
yHat10 = lwlrTest(abX[100:199],abX[0:99],abY[0:99],10)
print(rssError(abY[100:199],yHat01.T))
print(rssError(abY[100:199],yHat1.T))
print(rssError(abY[100:199],yHat10.T))

最小的核反而对应最大的误差，这就是过拟合

和简单线性回归对比

ws = standRegres(abX[0:99],abY[0:99])
yHat = np.mat(abX[100:199])*ws
print(rssError(abY[100:199],yHat.T.A))

 这个值与核为10时的值近似，但是这是最佳的嘛？或许是，但是如果想得到更好的结果，应该用10个不同的样本集做十次测试来比较结果。

 缩减系数来“理解”数据

如果数据的特征比样本点还多（n > m），也就是说输入数据的矩阵X不是满秩矩阵，非满秩矩阵在求逆时会出现问题。为了解决这个问题，统计学家引入了 岭回归（ridge regression） 的概念，这就是我们准备介绍的第一种缩减方法。接着是 lasso法，该方法效果很好但计算复杂。最后介绍了第二种缩减方法，称为 前向逐步回归，可以得到与lasso差不多的效果，且更容易实现。

岭回归

I是m*m单位矩阵，λ是一个用户定义的数值。 通过引入该惩罚项，能够减少不重要的参数，这个技术在统计学中也叫做 缩减（shrinkage）。

def redgeabo():
    abX,abY = loadDataSet('abalone.txt')
    ridegWeights = ridgeTest(abX,abY)
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(ridegWeights)
    plt.show()

横坐标为λ，纵坐标为回归系数。 在最左边，即λ最小时，可以得到所有系数的原始值（与线性回归一致）；而在右边，系数全部缩减成0；在中间部分的某值将可以取得最好的预测效果。为了定量地找到最佳参数值，还需要进行交叉验证。另外，要判断哪些变量对结果预测最具有影响力，在图中观察它们对应的系数大小就可以。

lasso

不难证明，在增加如下约束时，普通的最小二乘法回归会得到与岭回归的一样的公式：

上式限定了所有回归系数的平方和不能大于λ。使用普通的最小二乘法回归在当两个或更多的特征相关时，可能会得出一个很大的正系数和一个很大的负系数。正是因为上述限制条件的存在，使用岭回归可以避免这个问题。

与岭回归类似，另一个缩减方法lasso也对回归系数做了限定，对应的约束条件如下：

 唯一的不同点在于，这个约束条件使用绝对值取代了平方和。虽然约束形式只是稍作变化，结果却大相径庭：在λ足够小的时候，一些系数会因此被迫缩减到0，这个特性可以帮助我们更好地理解数据。这两个约束条件在公式上看起来相差无几，但细微的变化却极大地增加了计算复杂度（为了在这个新的约束条件下解出回归系数，需要使用二次规划算法）。

前向逐步回归

前向逐步回归算法可以得到与lasso差不多的效果，但更加简单。它属于一种贪心算法，即每一步都尽可能减少误差。一开始，所有的权重都设为1，然后每一步所做的决策是对某个权重增加或减少一个很小的值。

数据标准化，使其分布满足0均值和单位方差
在每轮迭代过程中：
	设置当前最小误差lowestError为正无穷
	对每个特征：
		增大或缩小：
			改变一个系数得到一个新的W
			计算新W下的误差
			如果误差Error小于当前最小误差lowestError：设置Wbest等于当前的W
		将W设置为新的Wbest

def regularize(xMat, yMat):
    inxMat = xMat.copy()               
    inyMat = yMat.copy()
    yMean = np.mean(yMat, 0)            #行与行操作，求均值
    inyMat = yMat - yMean               #数据减去均值
    inMeans = np.mean(inxMat, 0) #行与行操作，求均值
    inVar = np.var(inxMat, 0) #行与行操作，求方差
    inxMat = (inxMat - inMeans) / inVar #数据减去均值除以方差实现标准化
    return inxMat, inyMat

def stageWise(xArr, yArr, eps = 0.01, numIt = 100): #eps每次迭代的步长，numIt迭代次数
    xMat = np.mat(xArr); yMat = np.mat(yArr).T #数据集
    xMat, yMat = regularize(xMat, yMat) #数据标准化
    m, n = np.shape(xMat)
    returnMat = np.zeros((numIt, n))  #初始化numIt次迭代的回归系数矩阵
    ws = np.zeros((n, 1)) #初始化回归系数矩阵
    wsTest = ws.copy()
    wsMax = ws.copy()
    for i in range(numIt): #迭代numIt次
        print(ws.T) #打印当前回归系数矩阵
        lowestError = float('inf')  #正无穷
        for j in range(n): #遍历每个特征的回归系数
            for sign in [-1, 1]:
                wsTest = ws.copy()
                wsTest[j] += eps * sign #微调回归系数
                yTest = xMat * wsTest #计算预测值
                rssE = rssError(yMat.A, yTest.A) #计算平方误差
                if rssE < lowestError: #如果误差更小，则更新当前的最佳回归系数
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        returnMat[i,:] = ws.T  #记录numIt次迭代的回归系数矩阵
    return returnMat

    xArr,yArr = loadDataSet('abalone.txt')
    print(stageWise(xArr,yArr,0.01,200))

返回值

 发现w1和w6都是0，表明这些特征对目标值没有影响，也就是这些特征是不需要的。另外，在eps0.01的情况下，一段时间后系数已经饱和，并在特定值之间拉回震荡，如第一个权重在0.0.4和0.05之间震荡。可以用更小的步长和更多的步数：0.001和5000

可视化结果：

xArr,yArr = loadDataSet('abalone.txt')
returnMat = stageWise(xArr,yArr,0.001,5000)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(returnMat)
plt.show()

逐步线性回归算法的实际好处并不在于能绘出这样漂亮的图，主要的优点在于它可以帮助人们理解现有的模型并做出改进。当构建了一个模型后，可以运行该算法找出重要的特征，这样就有可能及时停止对那些不重要特征的收集。最后，如果用于测试，该算法每100次迭代后就可以构建出一个模型，可以使用类似于10折交叉验证的方法比较这些模型，最终选择使误差最小的模型。

预测乐高玩具套件的价格

获取数据

书中方式无法使用，从github上找到一个可下载的html文档

GitHub - Jack-Cherish/Machine-Learning at 1dd516f63fdf14fb538e4b8c5cfd7da4fcb77f7b

from bs4 import BeautifulSoup
def scrapePage(retX, retY, inFile, yr, numPce, origPrc):
     # 打开并读取HTML文件
    with open(inFile, encoding='utf-8') as f:
        html = f.read()
    soup = BeautifulSoup(html)
    i = 1
    # 根据HTML页面结构进行解析
    currentRow = soup.find_all('table', r = "%d" % i)
    while(len(currentRow) != 0):
        currentRow = soup.find_all('table', r = "%d" % i)
        title = currentRow[0].find_all('a')[1].text
        lwrTitle = title.lower()
        # 查找是否有全新标签
        if (lwrTitle.find('new') > -1) or (lwrTitle.find('nisb') > -1):
            newFlag = 1.0
        else:
            newFlag = 0.0
        # 查找是否已经标志出售，我们只收集已出售的数据
        soldUnicde = currentRow[0].find_all('td')[3].find_all('span')
        if len(soldUnicde) == 0:
            print("商品 #%d 没有出售" % i)
        else:
            # 解析页面获取当前价格
            soldPrice = currentRow[0].find_all('td')[4]
            priceStr = soldPrice.text
            priceStr = priceStr.replace('$','')
            priceStr = priceStr.replace(',','')
            if len(soldPrice) > 1:
                priceStr = priceStr.replace('Free shipping', '')
            sellingPrice = float(priceStr)
            # 去掉不完整的套装价格
            if  sellingPrice > origPrc * 0.5:
                print("%d\t%d\t%d\t%f\t%f" % (yr, numPce, newFlag, origPrc, sellingPrice))
                retX.append([yr, numPce, newFlag, origPrc])
                retY.append(sellingPrice)
        i += 1
        currentRow = soup.find_all('table', r = "%d" % i)

def setDataCollect(retX, retY):
    scrapePage(retX, retY, './lego/lego8288.html', 2006, 800, 49.99)  # 2006年的乐高8288,部件数目800,原价49.99
    scrapePage(retX, retY, './lego/lego10030.html', 2002, 3096, 269.99)  # 2002年的乐高10030,部件数目3096,原价269.99
    scrapePage(retX, retY, './lego/lego10179.html', 2007, 5195, 499.99)  # 2007年的乐高10179,部件数目5195,原价499.99
    scrapePage(retX, retY, './lego/lego10181.html', 2007, 3428, 199.99)  # 2007年的乐高10181,部件数目3428,原价199.99
    scrapePage(retX, retY, './lego/lego10189.html', 2008, 5922, 299.99)  # 2008年的乐高10189,部件数目5922,原价299.99
    scrapePage(retX, retY, './lego/lego10196.html', 2009, 3263, 249.99)  # 2009年的乐高10196,部件数目3263,原价249.99
if __name__ == '__main__':
    lgX = []
    lgY = []
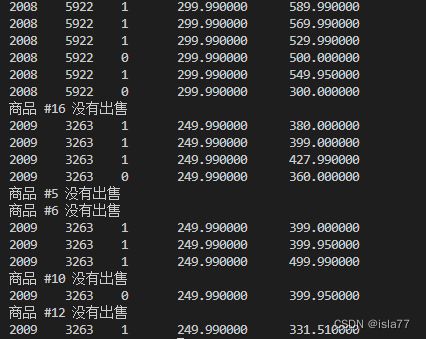
    setDataCollect(lgX, lgY)

结果

 这些特征分别为：出品年份、部件数目、是否为全新、原价、售价（二手交易）。

if __name__ == '__main__':
    lgX = []
    lgY = []    
    setDataCollect(lgX, lgY)
    #添加常数项特征X0(X0=1)，创建一个全1矩阵
    data_num, features_num = np.shape(lgX)
    lgX1 = np.mat(np.ones((data_num, features_num + 1))) 
    #将原数据放入1:5列
    lgX1[:, 1:5] = np.mat(lgX)
    #回归处理
    ws = standRegres(lgX1, lgY)
    print('%f%+f*年份%+f*部件数量%+f*是否为全新%+f*原价' % (ws[0], ws[1], ws[2], ws[3], ws[4]))

 通过输出具体模型可以看到，虽然这个模型能够吻合的很好，但是不太符合常理，与部件数量和全新参数成反比。

下面再用岭回归试验一次：

def crossValidation(xArr, yArr, numVal=10):
    m = len(yArr)  # 统计样本个数
    indexList = list(range(m))  # 生成索引值列表
    errorMat = np.zeros((numVal, 30))  # create error mat 30columns numVal rows
    for i in range(numVal):  # 交叉验证numVal次
        trainX = []
        trainY = []  # 训练集
        testX = []
        testY = []  # 测试集
        np.random.shuffle(indexList)  # 打乱次序
        for j in range(m):  # 划分数据集:90%训练集，10%测试集
            if j < m * 0.9:
                trainX.append(xArr[indexList[j]])
                trainY.append(yArr[indexList[j]])
            else:
                testX.append(xArr[indexList[j]])
                testY.append(yArr[indexList[j]])
        wMat = ridgeTest(trainX, trainY)  # 获得30个不同lambda下的岭回归系数
        for k in range(30):  # 遍历所有的岭回归系数
            matTestX = np.mat(testX)
            matTrainX = np.mat(trainX)  # 测试集
            meanTrain = np.mean(matTrainX, 0)  # 测试集均值
            varTrain = np.var(matTrainX, 0)  # 测试集方差
            matTestX = (matTestX - meanTrain) / varTrain  # 测试集标准化
            yEst = matTestX * np.mat(wMat[k, :]).T + np.mean(trainY)  # 根据ws预测y值
            errorMat[i, k] = rssError(yEst.T.A, np.array(testY))  # 统计误差
    meanErrors = np.mean(errorMat, 0)  # 计算每次交叉验证的平均误差
    minMean = float(min(meanErrors))  # 找到最小误差
    bestWeights = wMat[np.nonzero(meanErrors == minMean)]  # 找到最佳回归系数
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    meanX = np.mean(xMat, 0)
    varX = np.var(xMat, 0)
    unReg = bestWeights / varX  # 数据经过标准化，因此需要还原
    print('%f%+f*年份%+f*部件数量%+f*是否为全新%+f*原价' % (
    (-1 * np.sum(np.multiply(meanX, unReg)) + np.mean(yMat)), unReg[0, 0], unReg[0, 1], unReg[0, 2], unReg[0, 3]))
if __name__ == '__main__':
     lgX = []
     lgY = []    
     setDataCollect(lgX, lgY)    
     crossValidation(lgX, lgY)

 

可以看到，不但结果依然不符常理，且每次运行结果差异大。

但是我们可以看一下在缩减过程中回归系数是如何变化的

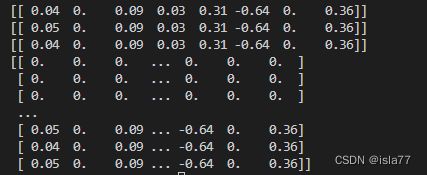
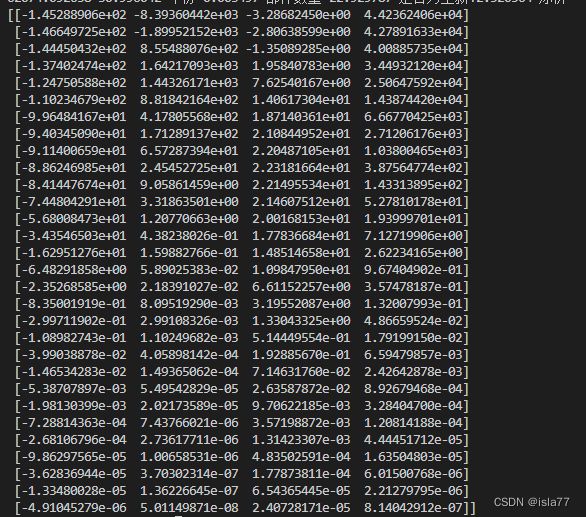
print(ridgeTest(lgX,lgY))

看运行结果的第一行，可以看到最大的是第4项，第二大的是第2项。

因此，如果只选择一个特征来做预测的话，我们应该选择第4个特征，也就是原始加个。如果可以选择2个特征的话，应该选择第4个和第2个特征。

这种分析方法使得我们可以挖掘大量数据的内在规律。在仅有4个特征时，该方法的效果也许并不明显；但如果有100个以上的特征，该方法就会变得十分有效：它可以指出哪个特征是关键的，而哪些特征是不重要的。