毫米波雷达原理介绍
毫米波雷达是指工作在波长为1-10mm的毫米波段,频率为30~300GHz。
基于其工作模式可以分为 “脉冲” 和 “连续波” 两种。其中,脉冲类型的毫米波雷达的原理与激光雷达相似都是采用TOF的方法。而连续波类型可以分为:CW恒频连续波,用于测速; FSK频移键控连续波,可探测单个目标的距离和速度,以及目前所采用的:FMCW调频连续波,探测多个目标的距离和速度。
本文后续则对FMCW调频连续波的测距、测速、测角原理进行详细叙述。
Chirp信号:线性调频脉冲
Chirp信号:是一个频率随着时间线性增加的正弦波,其在振幅时间表示中,如下所示。
我们把它换到频率时间图中,可以看到是一个 斜率S的直线。起始时刻fc=77GHz,在Tc 40微妙的时间中跨越4GHz的带宽,B与S是定义系统性能的重要参数。
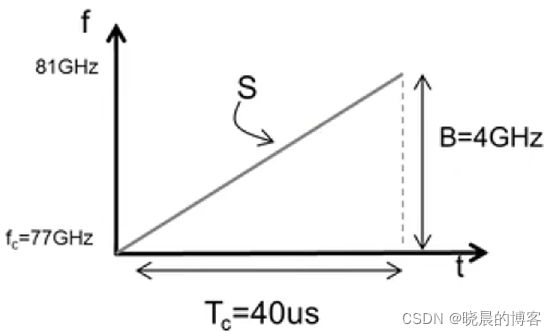
我们来简单看一下调频连续波毫米波雷达的工作过程:首先是合成器生成一个Chirp信号,然后通过TX天线发射,同时发送一份数据给混频器,遇到物体反射之后通过RX天线接收回波信号在混频器中生成一个中频信号。
混频器的工作原理如下:
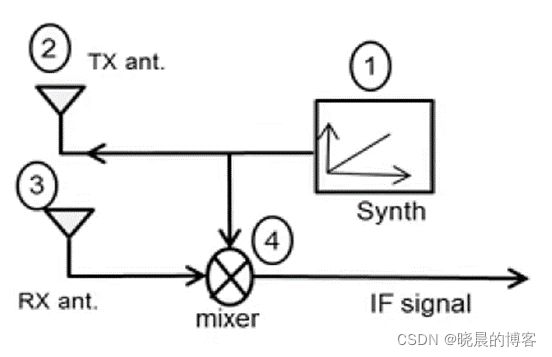
① 合成器生成一个Chirp信号
② TX天线发射
③ RX天线接收反射回来的线性调频脉冲
④ 混频器将TX与RX的信号进行混合,生成中频IF(intermediate frequency)信号
对于输入的两个正弦波,输出的正弦波角速度也就是频率是两个输入信号的差值,相位也是两个输入信号的差值。

IF中频信号及单个目标测距计算
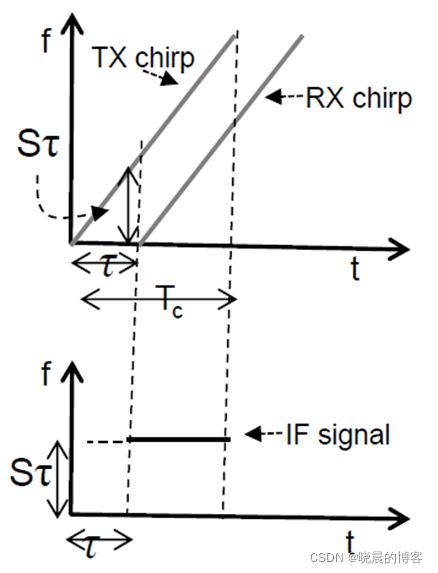
上方图中TX为发射信号,RX为接收信号。两者之间有一个时间延迟τ。
前面介绍混频器的作用时已经说过:混频器生成的IF信号在频率和相位两个方面都是两个输入信号直接相减,所以可以通过下方的f-t图进行表示,即一条频率恒定的直线。
时延τ为物体到雷达到物体所花费的往返时间,可以通过下述表示:

所以雷达前方的单个物体所生成的恒定频率的IF信号可以通过下述进行表示:
对此式稍微进行一些变换,得到物体到雷达的距离为:
距离分辨率
由雷达前方为一个物体推广到前方有多个物体。如右侧上方射频信号的 f-t 图像中所示,雷达发生一个Chrip信号,接收多个从不同物体反射的线性调频脉冲。则右侧下方的IF信号 f-t 图像中也与其对应。
我们前述已经了解到, IF信号的频率与物体到雷达的距离成正比,所以最下方代表物体距离最近,最上方代表物体距离最远。

在理想状态下,经过傅里叶变换,对应到频域中也会出现三个峰值。
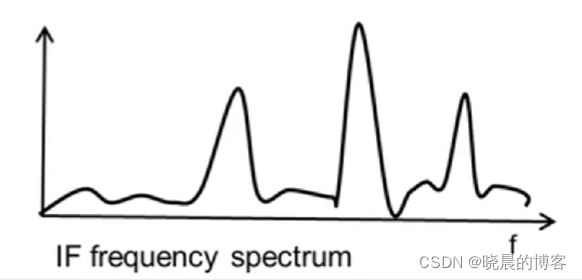
但是,在实际情况下,这并不一定成立。
针对两个物体:

已知:
IF信号的频率:

一个观测窗口 T 能够区分频率差异大于 1/T Hz的成分。
即:



最后,我们得到结论:距离分辨率取决于毫米波雷达Chirp信号的带宽。

举个例子,在4GHz带宽情况下,可以实现4 cm的距离分辨率。
最远观测距离
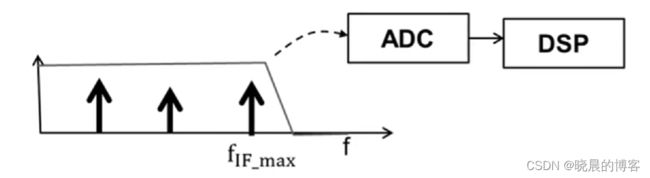
如上图所示,毫米波雷达在工作过程中会先对IF信号进行一个低通滤波,然后由ADC(analog to digital converter,模拟信号转换成数字信号)进行数字化,接着被发送到DSP(digital signal processing,数字信号处理器)中进行傅里叶变换估算物体的距离,以及进行后续其他估算物体速度、到达角等信息。
假设,想要观测的最远距离为: d m a x d_{max} dmax
由前述可知,最大观测距离对应IF信号的最大频率:

f I F _ m a x f_{IF\_max} fIF_max的值不能超过低通滤波器的阈值,即不能高于ADC的最大采样率 F s F_{s} Fs, f I F _ m a x < F s f_{IF\_max} < F_{s} fIF_max<Fs

所以,ADC的采样率 F s F_{s} Fs和斜率S限制了毫米波雷达的最远观测距离。
通常来说,雷达倾向于针对较大的 d m a x d_{max} dmax使用较小的斜率S。
存在问题
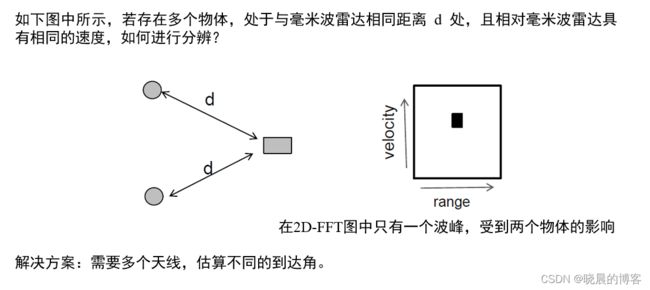
对于下图中的两个物体A、B到雷达具有相同的距离d,那么怎么区分二者呢?在range-FFT图像中能否出现两个独立的波峰?
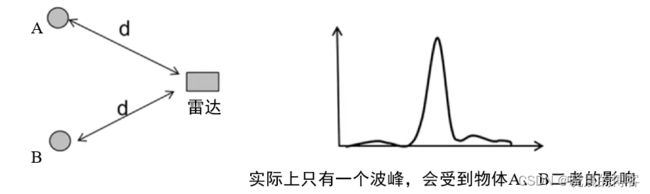
这样的话,我们如何区分两个物体呢?
如果物体A和物体B相对于毫米波雷达具有不同的速度,则可以通过进一步的信号处理进行分离,这需要IF信号的相位。
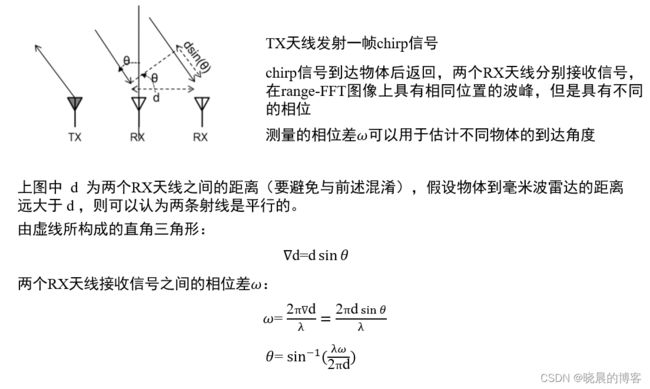
相位测量速度

IF信号: ( 2 π + φ 0 ) (2π+\varphi_0) Asin(2πft+φ0)
其中,频率 f = S 2 d c f=S\tfrac{2d}{c} f=Sc2d, φ 0 \varphi_0 φ0为TX chirp信号中A点的相位与RX chirp信号B点的相位之差。
假设物体移动了一小段距离,从而使得时间延迟变化为 τ + ▽ τ \tau+\triangledown\tau τ+▽τ。
TX信号中D点与A点的相位差: ▽ φ = 2 π f c ▽ τ \triangledown \varphi=2\pi f_c\triangledown\tau ▽φ=2πfc▽τ
代入: ▽ τ = 2 ▽ d c , ▽ φ = 4 π f c ▽ d c = 4 π ▽ d λ \triangledown\tau=\tfrac{2\triangledown d}{c}, \triangledown\varphi=\tfrac{4\pi f_c \triangledown d}{c}=\tfrac{4\pi \triangledown d}{\lambda } ▽τ=c2▽d,▽φ=c4πfc▽d=λ4π▽d
所以新的IF信号可以写为: ( 2 π + φ 0 + ▽ φ ) (2π+\varphi_0+\triangledown \varphi) Asin(2πft+φ0+▽φ)
其中, ▽ φ \triangledown \varphi ▽φ为物体微小移动引起的相位差 ▽ φ = 4 π ▽ d λ \triangledown \varphi=\tfrac{4\pi\triangledown d}{\lambda } ▽φ=λ4π▽d

如上方f-t图中所示,假设间隔时间 _ Tc发射两个相邻的TX chirp信号。其返回的IF信号在range FFT图像中波峰具有相同的位置,但相位不同,如下方range FFT图中所示。
两者之间的相位差对应了物体在 _ Tc时间间隔中的位移 v v_ vTc。
已知:
▽ φ = 4 π ▽ d λ \triangledown \varphi=\tfrac{4\pi\triangledown d}{\lambda } ▽φ=λ4π▽d
代入: ▽ d = v \triangledown d = v_ ▽d=vTc,得:
▽ φ = 4 π v λ \triangledown\varphi=\tfrac{4\pi v_}{\lambda } ▽φ=λ4πvTc
变换得:
v = λ ▽ φ 4 π v =\tfrac{\lambda \triangledown\varphi }{4\pi _} v=4πTcλ▽φ
由上述可得:通过两个连续chirp信号之间测量相位差,可以用于估算物体的速度。
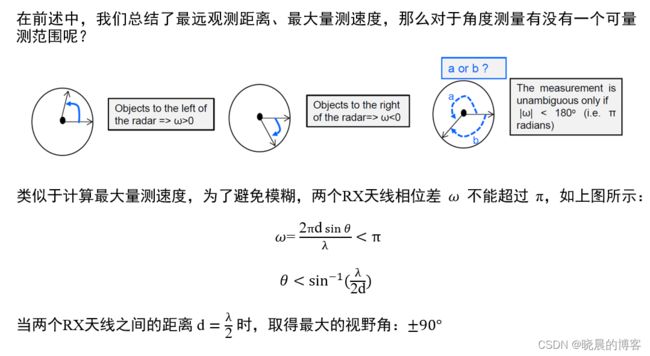
最大可量测速度

观察上图,当相位差 || 小于 π 时,才能够避免相互混淆的情况。即:
4 π v λ < π \tfrac{4\pi v_}{\lambda}<\pi λ4πvTc<π
v < 4 λ v<\tfrac{4_}{\lambda} v<λ4Tc
所以,针对一个毫米波雷达设备,其最大可量测速度为: v m a x = 4 λ v_{max}=\tfrac{4_}{\lambda} vmax=λ4Tc
式中, λ \lambda λ为波长, _ Tc 为相邻两个chirp信号脉冲之间的时间间隔,这表明如果我们想要测量更大的速度 v m a x v_{max} vmax ,则需要使用更密集的chirp信号。
速度分辨率
前述中我们推导出:单个物体的速度可以由通过两个连续chirp信号之间测量相位差进行计算,计算方式为:
v = λ ▽ φ 4 π v =\tfrac{\lambda \triangledown\varphi }{4\pi _} v=4πTcλ▽φ
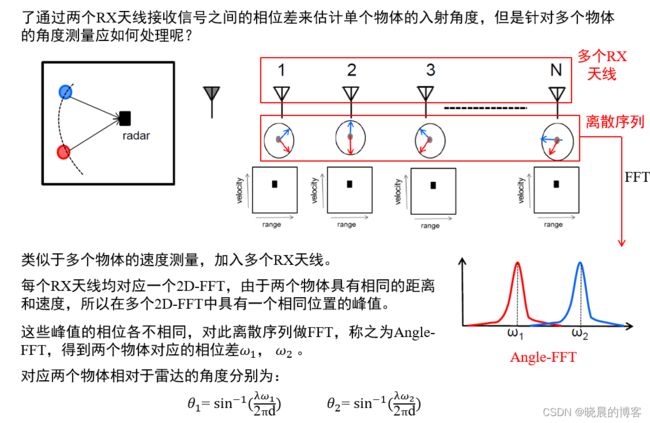
对于多个距离不同的物体,这种方法仍然适用,但是,针对我们所提出的问题“两个物体A、B到雷达具有相同的距离d,怎么计算二者的速度 1 _1 v1 和 2 _2 v2 ?”
解决方案:发射一系列等间隔的chirp信号(如下图中发射N个)