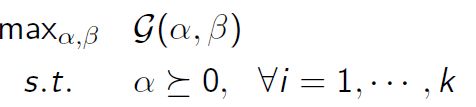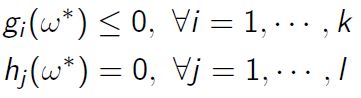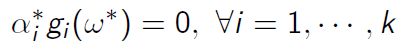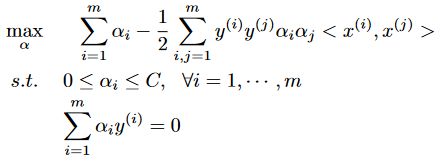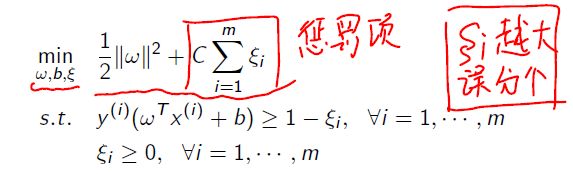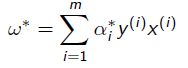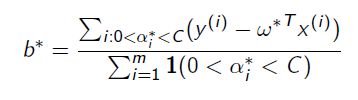山东大学机器学习实验五SVM
山东大学机器学习实验5报告
实验学时: 6 实验日期:2021.11.20
文章目录
- 山东大学机器学习实验5报告
-
- 实验题目 — Experiment 5 : SVM
- 实验目的
- 实验环境
-
- 软件环境
- 实验步骤与内容
-
-
- 了解SVM
- 二次规划求解
- Kernel Methods 核函数
- 软间隔SVM:
- Task 1: Linear SVM
-
- Plot decision boundary of the SVM
- Use the test data to evaluate the SVM classifier and show the fraction of test examples which were misclassified
- Try different values of the regularization term C, and report your observations.
- Task 2: Handwritten Digit Recognition(手写数字辨识之0 & 1)
-
- Preprocess Data
- Train Plain-vanilla SVM
- Experiment with different values of the regularization term C
- What value of C gives you the best training error on the dataset from part? & How does the test error for this choice of C compare with the test error you computed in part (i)?
- Task 3: Non-Linear SVM
-
- Plot the Data
- RBF kernel
- Task 4: Use SMO Instead Of QP solvers
-
- 结论分析与体会
-
-
-
- Different values Of C
- Different values Of C in Handwritten Digit Recognition
- γ \gamma γ 在Nonlinear SVM的影响
-
- Kernel函数
- SMO
-
-
- 实验源代码
实验题目 — Experiment 5 : SVM
实验目的
This exercise gives you practice with using SVMs for both linear and non-linear classification
使用 SVM 进行线性以及非线性分类
实验环境
软件环境
Windows 10 + Matlab R2020a
实验步骤与内容
了解SVM
SVM分类模型可以描述成下述模型:
但是上述模型的约束太多,所以我们可以变一下,得到对偶模型。
因为对偶问题约束简单 只有一个 α i > = 0 \alpha_i >= 0 αi>=0的约束
Lagrange dual problem:
Karush-Kuhn-Tucher(KKT) Condition
KKT条件:若强对偶则满足KKT条件:
- 稳定性
![]()
- Primal feasibility:
此外KKT条件是强对偶的充分条件,而我们求解对偶问题就是通过KKT条件进行求解的
应用核函数以及软间隔的SVM的Model 描述如下:
是
二次规划求解
本实验中需要求解QP问题,使用的是Matlab提供的quadprog 函数:
Kernel Methods 核函数
本质是对原始数据进行一个映射 或者是升维。
一般是把一个N维变为 N ∗ ( N − 1 ) ÷ 2 N*(N-1) \div 2 N∗(N−1)÷2维度
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-F0HfSHPO-1637667157053)(C:/Users/12042/AppData/Roaming/Typora/typora-user-images/image-20211121201415845.png)]
软间隔SVM:
即允许有一些被误分类,但是限制数量
然后 ξ i \xi_i ξi 是slack variable 松弛变量(类似于正则惩罚项)
所以model 变为:
C 权衡margin 以及 misclassification
比如 small C: 那么就代表想要一个比较大的间隔
large C: 表示想要更少的误分类
对应的拉格朗日函数:
![]()
加了一个 " r " 需要求五个参数: ω b ξ α r \omega \, b \, \xi \, \alpha \, r ωbξαr
通过QP问题求解得到 α \alpha α
然后通过对偶 + KKT得到
Task 1: Linear SVM
Plot decision boundary of the SVM
首先读入数据,画出散点图:数据集一的如下:可以看出具有明显的线性分界Boudary
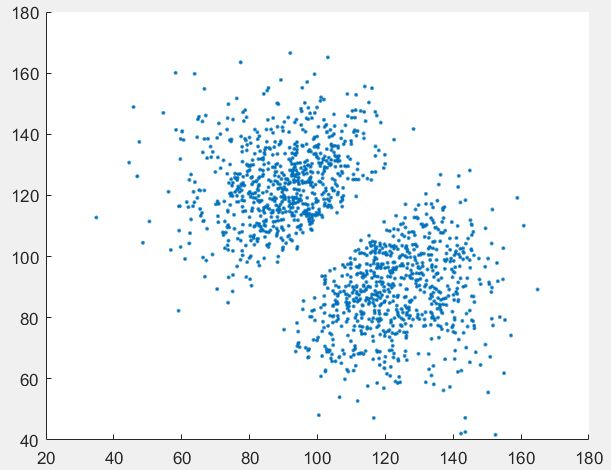
下图是数据集二的:分解间隔不如一明显但是还是能看出来是有的
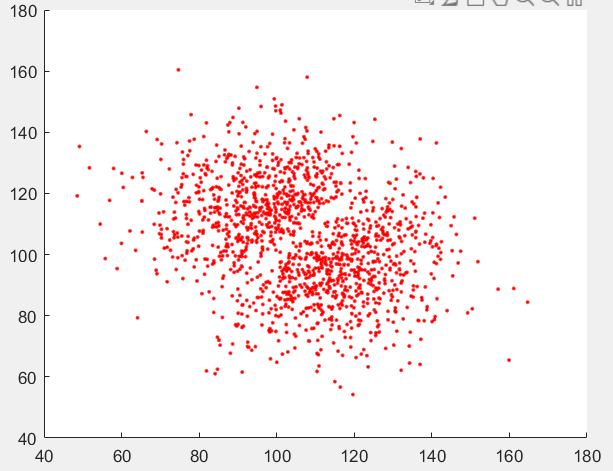
之后利用QP问题的求解器:quadprog进行求解
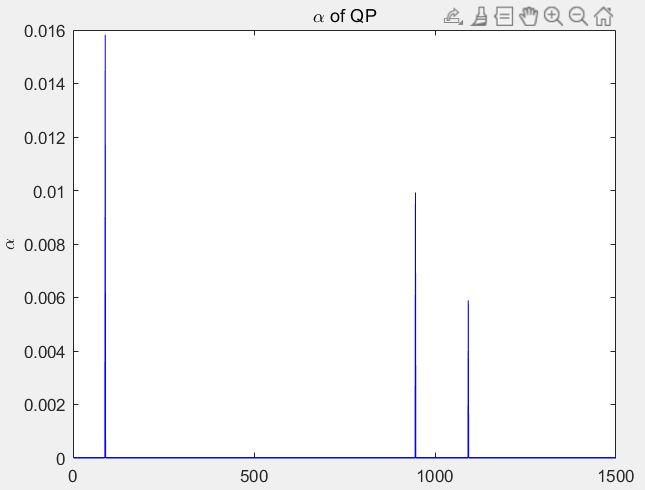
得到 α \alpha α 的值
这里有个问题:matlab 求出来的存在一些 α \alpha α数量级大概在 -18次方,这些认为是求出来就是0的,进行一个处理得到 α \alpha α如下两张图 分别是data1data2 C很大的情况下求出的 α \alpha α
对DataSet1 即如果选择一个比较大的C 误分类少的话, 求出的Support Vector 只有三个,这样只有把C降到0.016 才会开始有限制作用
对DataSet12 即如果选择一个比较大的C 误分类少的话, 求出的Support Vector 只有三个,这样只有把C降到1.5 才会开始有限制作用
所以如果使用一个较大的C来训练DataSet1 得到效果如下图,即就是Hard Margin
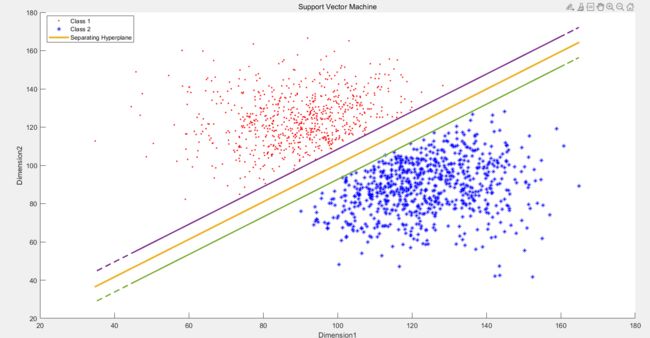
所以如果使用一个较小的C来训练DataSet1 得到效果如下图,即就是Soft Margin,没有误分类的点,但是有落在boundary之内的点
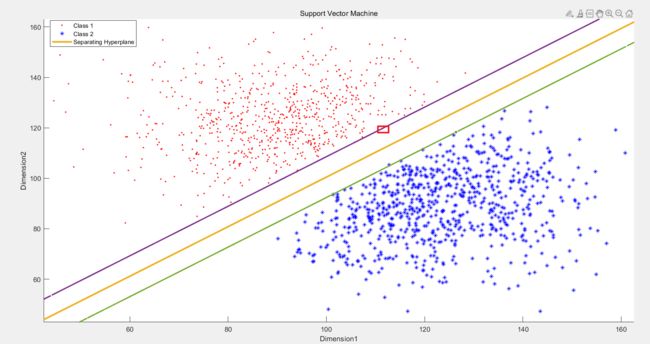
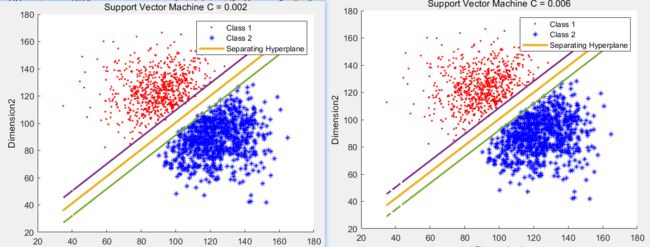
对Dataset2 也是同理C 较大时:
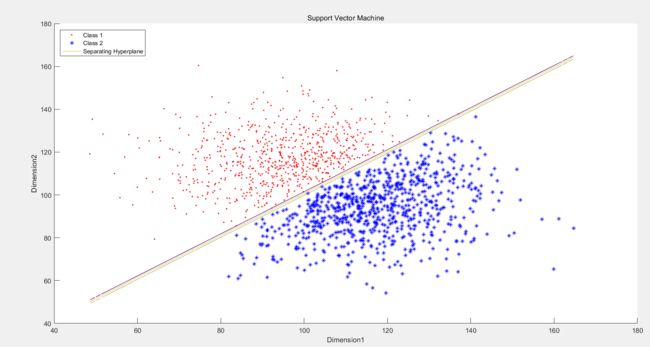
对Dataset2 也是同理C 较小时:
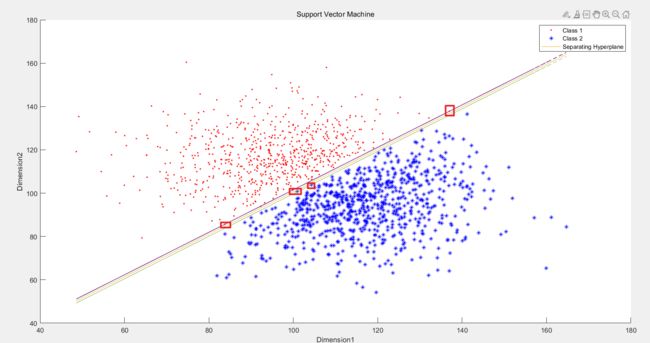
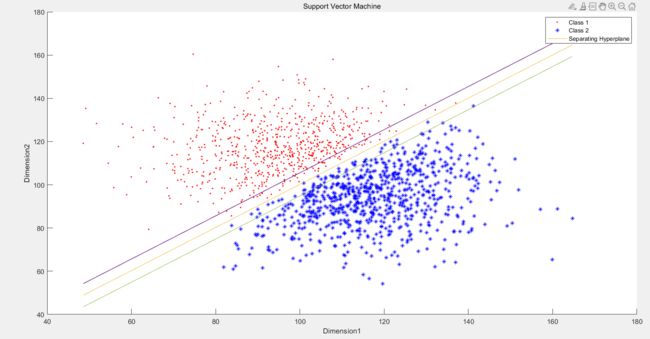
Use the test data to evaluate the SVM classifier and show the fraction of test examples which were misclassified
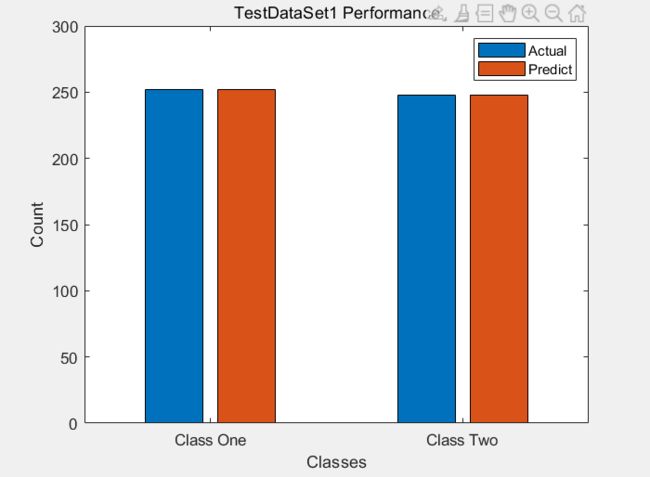
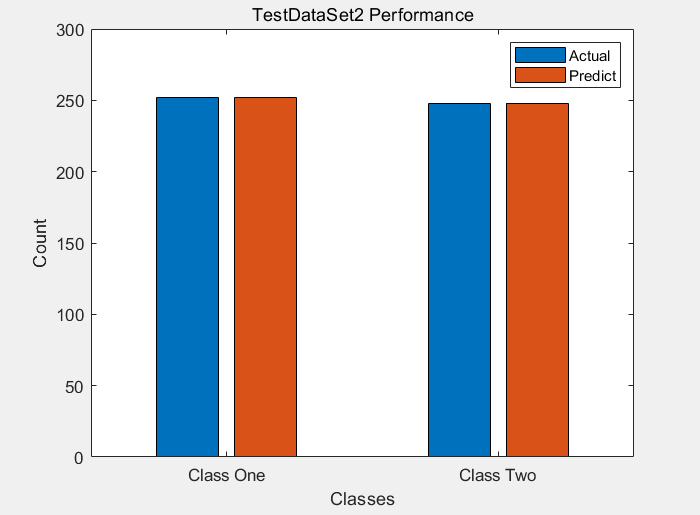
首先: 两个 test data 的表现情况时: Accuracy = 100% 故不存在误分类, 画出分类效果柱状图
test Data的表现情况: 可以看到 没有误分类的!
Try different values of the regularization term C, and report your observations.
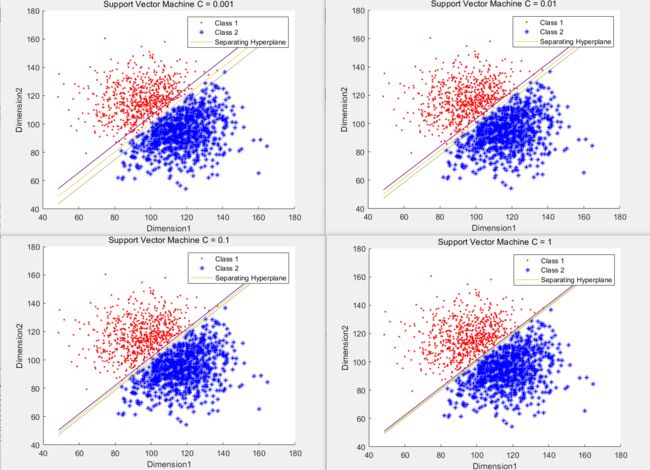
数据一 设置 C = 0.001 : 0.001 : 0.01
进行测试发现所有的score 都是 100%
然后部分boundary图片如下图
关于DataSet2 使用C = 0.001 - 0.01
准确率仍都是100% 不再展示
仅展示部分情况
Task 2: Handwritten Digit Recognition(手写数字辨识之0 & 1)
Preprocess Data
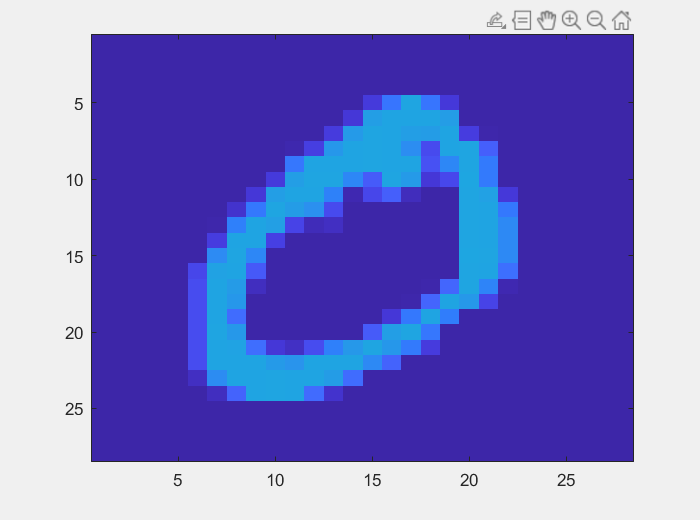
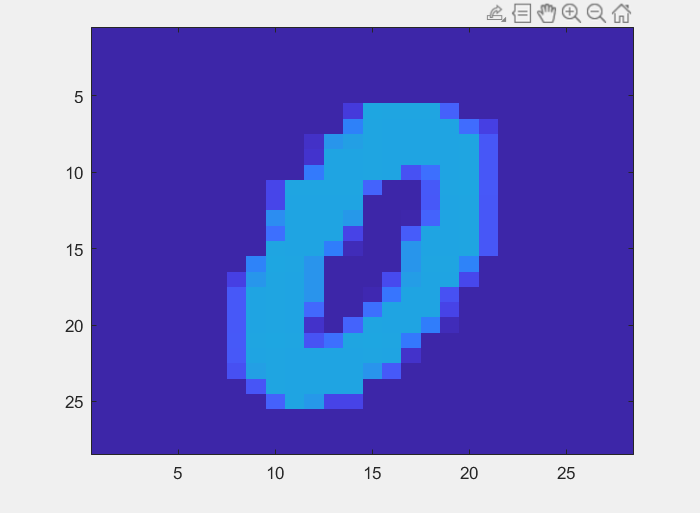
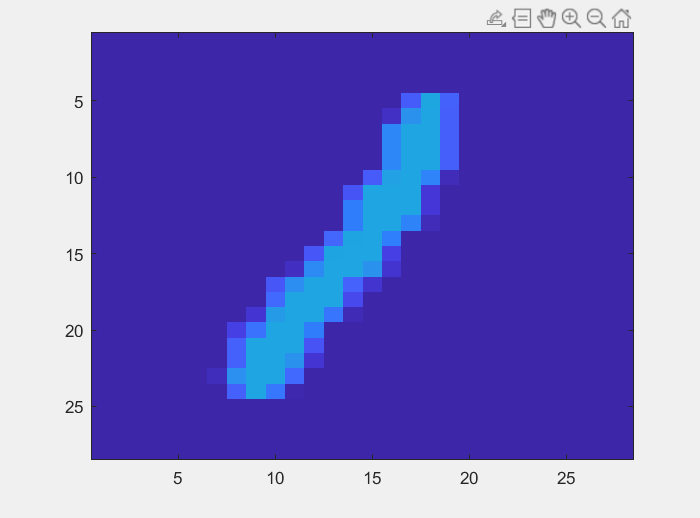
处理数据,对于给的image的数据进行一个简单的处理,能够得到image的大体情况:
即使用灰度值直接画出的
此外,本题Image张量的SIZE = 1 X 28 X 28 然后使用extractLBPFeatures() 来将feature 进行 一个Pooling + Flatten 得到一个 1X1X59的feature
对应SVM中就是有59个feature( X i X_i Xi) 然后 进行train
Train Plain-vanilla SVM
使用12000+图片数据会出现
因为数据太大了 写QPsolver 的H矩阵都是 1w X 1w size的 太大了! 可能自己电脑也有问题
所以 缩小以下规模 每次随机不重复采样1000个image 来train
返回采样数据以及对应的标签以及在原set中的位置
%%
function [sample_Datas,sample_labels,chose_set] = sample_random(num,datas,labels)
% datas 为原始数据 num 为目标数目
chose_set = [];%1000*1 即这1000个数在原来set中的id
R = length(datas);
a = rand(R,1);
[b,c] = sort(a);
chose_set = c(1:num,1);
chose_set = sort(chose_set);
sample_Datas = datas(chose_set,:);
sample_labels = labels(chose_set,:);
end
训练完成之后 不适用soft margin 得到的准确率大概是**99.4%——99.5%**左右
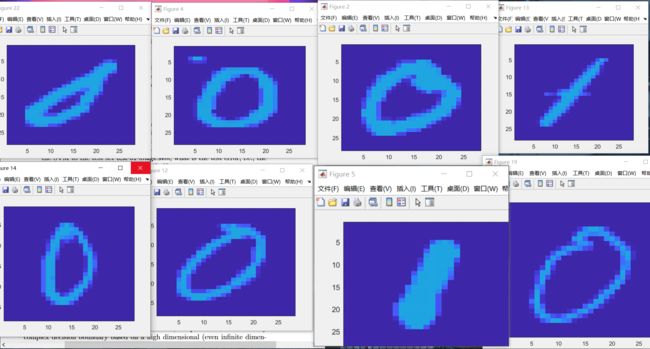
例如有一次有六个误分类(Training Data中的)他们的图片如下图:
![]()
可以比较清晰的看出来 例如中间的 ‘2’ 下面扁平的1 以及最后一个 ‘6’ 都是很有可能本身就存在误分类的,他们不符合0 1 的feature
进行测试:
得到准确率 = 98.58 23张image error 部分展示如下
可能的原因就是 书写不规范 既不像0 也不是1 feature 不够明显
Experiment with different values of the regularization term C
Pick 10 个 values
C = [0.01 0.05 0.1 0.5 1.5 3 5 7.5 10 15]; 进行训练+测试
发现在C=0.1 以后就准确率达到90%了
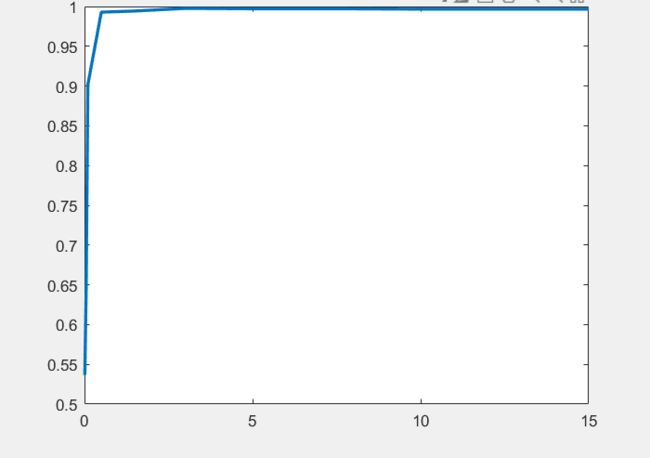
所以 更细致的分以下C = 0.02 : 0.02 : 0.2 结果如下:进行了两次测试 尽量避免随机采样的影响
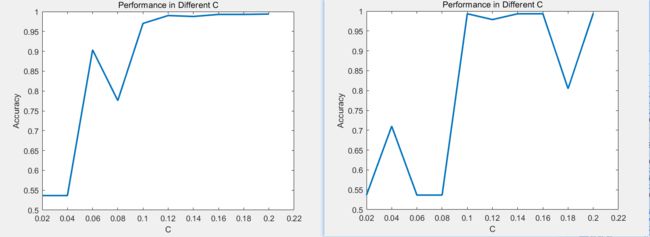
即 Larger C 意味着 更少的misclassfication and Higher Accuracy
What value of C gives you the best training error on the dataset from part? & How does the test error for this choice of C compare with the test error you computed in part (i)?
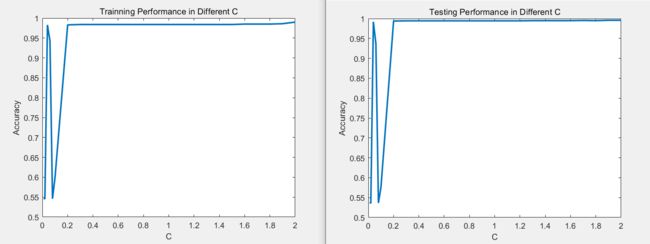
采样25个C 进行训练,得到训练误差以及对应的测试误差
当C = 2时,train的效果最好时0.9900,但是当C=1.8时,test效果最好是0.9957
总之C越大,可能存在过拟合,导致在train上效果变好,但是test上变差
Task 3: Non-Linear SVM
Plot the Data
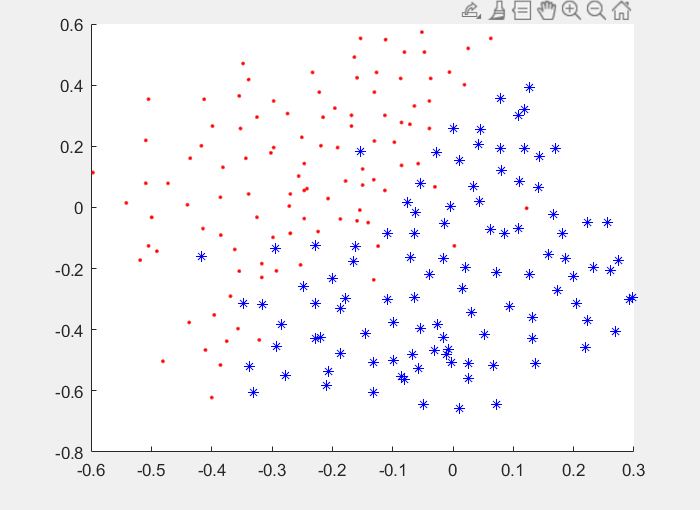
发现没有很明显的线性分界线
所以需要使用一个kernel 进行升维,期待数据在高维空间存在一个线性可分的超平面
RBF kernel
即高斯核函数
本次实验中写作:
![]()
此时模型写作:
![]()
使用RBF kernel 进行测试;
γ = [ 1 ; 10 ; 100 ; 1000 ] \gamma = [1;10;100;1000] γ=[1;10;100;1000]
可以发现随着 γ \gamma γ增加 分类效果虽然变好 但是逐渐分类过拟合
![]()
Task 4: Use SMO Instead Of QP solvers
编写一个建议的SMO算法来代替求解大规模的QP问题
Input:数据、标签、参数bias 以及最大迭代次数和容忍值
Algorithm: 每次迭代
根据规则选两个 α \alpha α
保持其他拉格朗日乘子不变,更新 α 1 α 2 \alpha_1\, \alpha_2 α1α2
output: α b i a s \alpha \, bias αbias
写了一个简化版的SMO算法
遍历选一个 α 1 \alpha_1 α1 然后随机选取一个 α 2 \alpha_2 α2 但是这个 α 2 \alpha_2 α2必须满足条件:

结论分析与体会
-
Different values Of C
在前两个数据集中,不同的C对于最后的准确率没有影响,都是100%,说明这两个数据集都存在一个线性可分的超平面。 但是C对于所决定的boundary的范围是有影响的,C越小,从而导致惩罚项权重变小,就会导致一个更大的margin,但是可能存在更多的误分类。
-
Different values Of C in Handwritten Digit Recognition
在手写数字辨识里面,只要C大于一定值,例如0.1,之后准确率都可以稳定在99%左右,在我进行实验测试中,C=2是train准确率最高 99%,C=1.8时,test效果最好是0.9957
总之C越大,可能存在过拟合,导致在train上效果变好,但是test上变差
-
γ \gamma γ 在Nonlinear SVM的影响
随着 γ \gamma γ增大会逐渐过拟合,所以需要平衡 γ \gamma γ
-
Kernel函数
本实验选取RBF kernel 即高斯核函数,注意使用核函数不需要算 ϕ \phi ϕ 只需要计算出 矩阵 K即可
-
SMO
SMO就是把一个大的二次规划转化成多个小的二次规划
for i=1:iter
a. 根据预先设定的规则,从所有样本中选出两个
b. 保持其他拉格朗日乘子不变,更新所选样本对应的拉格朗日乘子
end
如何更新 α 1 α 2 \alpha1 \, \alpha2 α1α2呢?

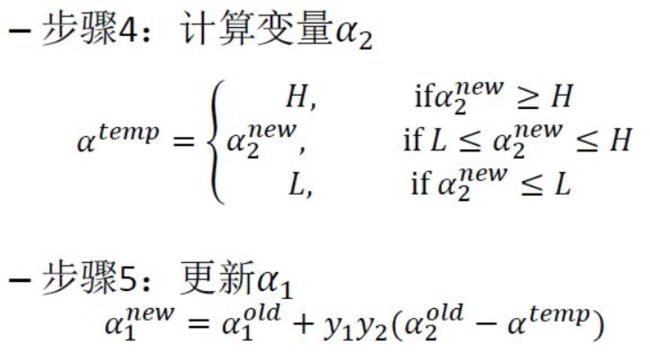
简化时随机选取,所以导致效果一般
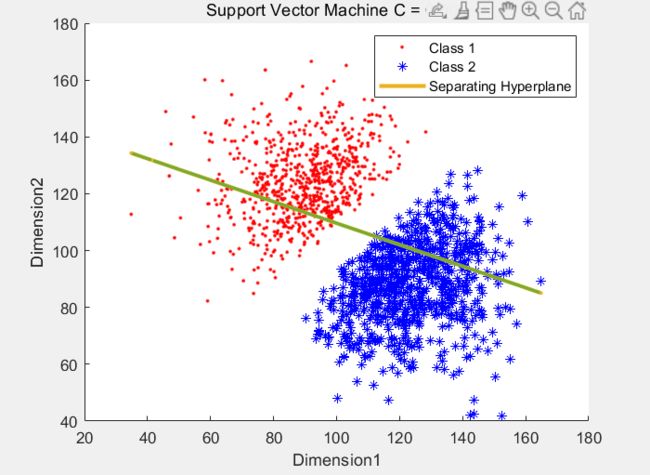
可能是训练次数太少,虽然这个分界线比较离谱,但是准确率还可以有73.6%
代码见最后
实验源代码
Lab51.m:
%% 实验五 SVM 支持向量机
%% 软间隔
%% 读数据 画散点图
clear,clc;
Trainning_Datas = load('training_1.txt');
Data_x1 = Trainning_Datas(:,1);
Data_x2 = Trainning_Datas(:,2);
Data_label = Trainning_Datas(:,3);
X = [Data_x1,Data_x2];
Y = Data_label;
% scatter(Data_x1,Data_x2,'.','b');
%% 利用quadprog 求解 $\alpha$
% 求Min 1/2 yax - a
%目标函数必须写处一个二次型H和一个矩阵相加的形式
% Cs = 0.001:0.001:0.01; % 超参
% for num = 1 : 10
H=[];%目标函数的H
C = 0.006;
for i=1:length(X)%对于所有样本都要遍历
for j=1:length(X)
H(i,j)=X(i,:)*(X(j,:))'*Y(i)*Y(j);
end
end
F = -1 * ones(length(X),1);%目标函数的F
%等式约束
aeq=Y';
beq=zeros(1,1);
%不等式约束 没有
ub=[];
ib=[];
%自变量约束
lb = zeros(length(X),1);%下界
ub = zeros(length(X),1);%上界
ub(:,:) = C;
% 求解alpha
[alpha,fval]=quadprog(H,F,[],[],aeq,beq,lb,ub);%二次规划问题
%% 会求出很多alpha十分接近于0 那种不是support vector
% 但是 大概多少个点合适呢?? 大概就是三个 因为那个分界线还是很明显的
% BUT 软间隔要全算 so 没必要分了
% 注意!! data1 明显不需要软间隔 所有没有误分类!(除非C很小~)
% 就是正常大概是0.01 刚出头
plot(alpha,'b') %明显
title('\alpha of QP')
xlabel('x')
ylabel('\alpha')
a = alpha;
% 还是选择处理一下 因为正常来说是有=0的
for i=1:length(a)
if a(i)<1e-8
a(i)=0;
end
end
%% 求w
W = 0; % 系数矩阵
u = 0;
j = find(a > 0 & a < C);
for i = 1:length(X)
W = W + a(i)*Y(i)*X(i,:)';
end
%% 求r
R = 0;
R = C - a;
%% 求B 是用的support vector
% 有点问题... 就是 只用S V 还是全用
% 公式是S V 但是 算出来的SV 和 理想SV不一样
j = find(a > 0 & a < C); %找 S V
nums = length(j); % 多少个
temp = Y - X*W;
B = sum(temp(j)) / nums;
%% 画出Boundary
k = -W(1)./W(2);
bb = -B./W(2);
group1 = find(Data_label==1);
group2 = find(Data_label==-1);
scatter(Data_x1(group1),Data_x2(group1),'.','r');
hold on
scatter(Data_x1(group2),Data_x2(group2),'*','b');
hold on
yy = k.*Data_x1 + bb;
plot(Data_x1,yy,'-','LineWidth',2.5)
hold on
yy = k.*Data_x1 + bb + 1./W(2);
plot(Data_x1,yy,'--','LineWidth',2)
hold on
yy = k.*Data_x1 + bb - 1./W(2);
plot(Data_x1,yy,'--','LineWidth',2)
title('Support Vector Machine C = 0.006')
xlabel('Dimension1')
ylabel('Dimension2')
legend('Class 1','Class 2','Separating Hyperplane')
%% Test
Predict = [];
Test_Datas = load('test_1.txt');
test_x1 = Test_Datas(:,1);
test_x2 = Test_Datas(:,2);
test_X = [test_x1,test_x2];
test_Y = Test_Datas(:,3);
Predict = sign(test_X*W + B);
Judge=(Predict==test_Y);
score = sum(Judge)./length(test_X)
%% Draw Bar on testdata
test_Class1_nums = length(find(test_Y==1));
test_Class2_nums = length(find(test_Y==-1));
Predict_Class1_nums = length(find(Predict==1));
Predict_Class2_nums = length(find(Predict==-1));
Bar_y = [test_Class1_nums,Predict_Class1_nums;test_Class2_nums,Predict_Class2_nums];
Bar_x = categorical({'Class One','Class Two'});
bar(Bar_x,Bar_y)
legend('Actual','Predict');
xlabel('Classes');
ylabel('Count');
title(['TestDataSet1 Performance']);
Lab52.m
%% 实验五 SVM 支持向量机
%% 软间隔
%% 读数据 画散点图
clear,clc;
Trainning_Datas = load('training_2.txt');
Data_x1 = Trainning_Datas(:,1);
Data_x2 = Trainning_Datas(:,2);
Data_label = Trainning_Datas(:,3);
X = [Data_x1,Data_x2];
Y = Data_label;
%scatter(Data_x1,Data_x2,'.','r');
%% 利用quadprog 求解 $\alpha$
% 求Min 1/2 yax - a
%目标函数必须写处一个二次型H和一个矩阵相加的形式
C = 1; % 超参
H=[];%目标函数的H
for i=1:length(X)%对于所有样本都要遍历
for j=1:length(X)
H(i,j)=X(i,:)*(X(j,:))'*Y(i)*Y(j);
end
end
F = -1 * ones(length(X),1);%目标函数的F
%等式约束
aeq=Y';
beq=zeros(1,1);
%不等式约束 没有
ub=[];
ib=[];
%自变量约束
lb = zeros(length(X),1);%下界
ub = zeros(length(X),1);%上界
ub(:,:) = C;
% 求解alpha
[alpha,fval]=quadprog(H,F,[],[],aeq,beq,lb,ub);%二次规划问题
%% 会求出很多alpha十分接近于0 那种不是support vector
% 但是 大概多少个点合适呢?? 大概就是三个 因为那个分界线还是很明显的
% BUT 软间隔要全算 so 没必要分了
% 注意!! data1 明显不需要软间隔 所有没有误分类!(除非C很小~)
% 就是正常大概是0.01 刚出头
plot(alpha,'b') %明显
title('\alpha of QP')
xlabel('x')
ylabel('\alpha')
a = alpha;
% 还是选择处理一下 因为正常来说是有=0的
for i=1:length(a)
if a(i)<1e-8
a(i)=0;
end
end
%% 求w
W = 0; % 系数矩阵
u = 0;
j = find(a > 0 & a < C);
for i = 1:length(X)
W = W + a(i)*Y(i)*X(i,:)';
end
%% 求r
R = 0;
R = C - a;
%% 求B 是用的support vector
% 有点问题... 就是 只用S V 还是全用
% 公式是S V 但是 算出来的SV 和 理想SV不一样
j = find(a > 0 & a < C); %找 S V
nums = length(j); % 多少个
temp = Y - X*W;
B = sum(temp(j)) / nums;
%% 画出Boundary
k = -W(1)./W(2);
bb = -B./W(2);
figure
group1 = find(Data_label==1);
group2 = find(Data_label==-1);
scatter(Data_x1(group1),Data_x2(group1),'.','r');
hold on
scatter(Data_x1(group2),Data_x2(group2),'*','b');
hold on
yy = k.*Data_x1 + bb;
plot(Data_x1,yy,'-','LineWidth',0.5)
hold on
yy = k.*Data_x1 + bb + 1./W(2);
plot(Data_x1,yy,'--','LineWidth',1)
hold on
yy = k.*Data_x1 + bb - 1./W(2);
plot(Data_x1,yy,'--','LineWidth',0.5)
title('Support Vector Machine C = 1')
xlabel('Dimension1')
ylabel('Dimension2')
legend('Class 1','Class 2','Separating Hyperplane')
%% Test
Predict = [];
Test_Datas = load('test_2.txt');
test_x1 = Test_Datas(:,1);
test_x2 = Test_Datas(:,2);
test_X = [test_x1,test_x2];
test_Y = Test_Datas(:,3);
Predict = sign(test_X*W + B);
Judge=(Predict==test_Y);
score = sum(Judge)./length(test_X)
%% Draw Bar on testdata
figure
test_Class1_nums = length(find(test_Y==1));
test_Class2_nums = length(find(test_Y==-1));
Predict_Class1_nums = length(find(Predict==1));
Predict_Class2_nums = length(find(Predict==-1));
Bar_y = [test_Class1_nums,Predict_Class1_nums;test_Class2_nums,Predict_Class2_nums];
Bar_x = categorical({'Class One','Class Two'});
bar(Bar_x,Bar_y)
legend('Actual','Predict');
xlabel('Classes');
ylabel('Count');
title(['TestDataSet2 Performance']);
Lab53.m
%% Hand
clc,clear;
% 存一个map 这1000个sampledata里面 对应于原来的第几个
[Train_Data_X,Train_Labels] = strimage();
[Train_Data_X,Train_Labels,Map_id] = sample_random(1000,Train_Data_X,Train_Labels);
%Size = 12665 * 59
%%
Cs = 0.02:0.02:0.2;
for Cnum=1:10
C = Cs(Cnum); % 超参
H=[];%目标函数的H
for i=1:length(Train_Data_X)%对于所有样本都要遍历
for j=1:length(Train_Data_X)
H(i,j)=Train_Data_X(i,:)*(Train_Data_X(j,:))'*Train_Labels(i)*Train_Labels(j);
end
end
F = -1 * ones(length(Train_Data_X),1);%目标函数的F
%%
%等式约束
aeq=Train_Labels';
beq=zeros(1,1);
%不等式约束 没有
ub=[];
ib=[];
%自变量约束
lb = zeros(length(Train_Data_X),1);%下界
ub = [];%没有上界要求
ub = zeros(length(Train_Data_X),1);%上界
ub(:,:) = C;
% 求解alpha
[alpha,fval]=quadprog(H,F,[],[],aeq,beq,lb,ub);%二次规划问题
%%
% plot(alpha,'b') %明显
% title('\alpha of QP')
% xlabel('x')
% ylabel('\alpha')
a = alpha;
% 还是选择处理一下 因为正常来说是有=0的
for i=1:length(a)
if a(i)<1e-8
a(i)=0;
end
end
%% 求W
W = 0; % 系数矩阵
u = 0;
j = find(a > 0);
for i = 1:length(Train_Data_X)
W = W + a(i)*Train_Labels(i)*Train_Data_X(i,:)';
end
%%
j = find(a > 0); %找 S V
nums = length(j); % 多少个
temp = Train_Labels - Train_Data_X*W;
B = sum(temp(j)) / nums;
%%
% Predict = [];
% test_X = Train_Data_X;
% test_Y = Train_Labels;
% Predict = sign(test_X*W + B);
% Judge=(Predict==test_Y);
% score = sum(Judge)./length(test_X)
%% 找误分类的
% misclass =[];
% misclass = find(Judge==0)
% for i=1:length(misclass)
% id = misclass(i);
% ori_id = Map_id(id);
% showimage(ori_id)
% end
%% Test
[Test_Data_X,Test_Labels] = strimagetest();
Predict = [];
test_X = Test_Data_X;
test_Y = Test_Labels;
Predict = sign(test_X*W + B);
Judge=(Predict==test_Y);
score(Cnum) = sum(Judge)./length(test_X)
%% 找误分类的
% misclass =[];
% misclass = find(Judge==0)
% for i=1:length(misclass)
% id = misclass(i);
% ori_id = Map_id(id);
% showimage(ori_id)
% end
end
figure
plot(Cs,score,'LineWidth',2)
title('Performance in Different C')
xlabel('C')
ylabel('Accuracy')
ylim([0.5 1])
axis()
%%
function [sample_Datas,sample_labels,chose_set] = sample_random(num,datas,labels)
% datas 为原始数据 num 为目标数目
chose_set = [];%1000*1 即这1000个数在原来set中的id
R = length(datas);
a = rand(R,1);
[b,c] = sort(a);
chose_set = c(1:num,1);
chose_set = sort(chose_set);
sample_Datas = datas(chose_set,:);
sample_labels = labels(chose_set,:);
end
修改过后的strimage.m
function [AllPic_Feature,All_Labels] = strimage()
fidin = fopen('train-01-images.svm'); % 打开test2.txt文件
j = 1;
apres = [];
AllPic_Feature = [];
All_Labels=[];
while ~feof(fidin)
tline = fgetl(fidin); % 从文件读行
apres{j} = tline;
% 处理该行
a = char(apres(j));
All_Labels = [All_Labels;str2num(a(1:2))];
lena = size(a);
lena = lena(2);
xy = sscanf(a(4:lena), '%d:%d');
lenxy = size(xy);
lenxy = lenxy(1);
grid = [];
grid(784) = 0;
for i=2:2:lenxy %% 隔一个数
if(xy(i)<=0)
break
end
grid(xy(i-1)) = xy(i) * 100/255;
end
grid1 = reshape(grid,28,28);
grid1 = fliplr(diag(ones(28,1)))*grid1;
grid1 = rot90(grid1,3);
image_f = extractLBPFeatures(grid1);
AllPic_Feature = [AllPic_Feature;image_f];
j = j+1;
end
end
showimage.m:
function showimage(n)
fidin = fopen('train-01-images.svm'); % 打开test2.txt文件
i = 1;
apres = [];
while ~feof(fidin)
tline = fgetl(fidin); % 从文件读行
apres{i} = tline;
i = i+1;
end
a = char(apres(n));
lena = size(a);
lena = lena(2);
xy = sscanf(a(4:lena), '%d:%d');
lenxy = size(xy);
lenxy = lenxy(1);
grid = [];
grid(784) = 0;
for i=2:2:lenxy %% 隔一个数
if(xy(i)<=0)
break
end
grid(xy(i-1)) = xy(i) * 100/255;
end
grid1 = reshape(grid,28,28);
grid1 = fliplr(diag(ones(28,1)))*grid1;
grid1 = rot90(grid1,3);
figure
image(grid1)
hold on;
end
Lab54.m
%% Non-Linear SVM
clear,clc
Trainning_Datas = load('training_3.txt');
Data_x1 = Trainning_Datas(:,1);
Data_x2 = Trainning_Datas(:,2);
Data_label = Trainning_Datas(:,3);
X = [Data_x1,Data_x2];
Y = Data_label;
group1 = find(Data_label==1);
group2 = find(Data_label==-1);
scatter(Data_x1(group1),Data_x2(group1),'.','r');
hold on
scatter(Data_x1(group2),Data_x2(group2),'*','b');
hold on
%%
gammas = [1 10 100 1000];
for gnum = 1:4
gamma = gammas(gnum);
%求Kernel 矩阵
Knel = get_kernel_matrix(X,gamma);
H=[];
for i=1:length(X)
for j = 1:length(X)
H(i,j) = Knel(i,j)*Y(i)*Y(j);
end
end
F=-1*ones(length(X),1);%目标函数的F
aeq = Y';
beq=zeros(1,1);
ub=[];
ib=[];
%自变量约束
lb=zeros(length(X),1);
ub=[];
[alpha,fval]=quadprog(H,F,ib,ub,aeq,beq,lb,ub);
%%
a = alpha;
epsilon = 1e-5;
%查找支持向量
sv_index = find(abs(a)> epsilon);
Xsv = X(sv_index,:);
Ysv = Y(sv_index);
svnum = length(sv_index);
sum_b = 0;
for k = 1:svnum
sum = 0;
for i = 1:length(X)
sum = sum + a(i,1)*Y(i,1)*Knel(i,k);
end
sum_b = sum_b + Ysv(k) - sum;
end
B = sum_b/svnum;
% W不用直接求解
%% Make Classfication Predictions over a grid of values
xplot = linspace (min(X( : , 1 ) ) , max(X( : , 1 ) ),100 )';
yplot = linspace (min(X( : , 2 ) ) , max(X( : , 2 ) ) ,100)';
[XX, YY] = meshgrid(xplot,yplot);
vals = zeros(size(XX));
%% 计算vals using SVM
for i=1:length(vals)
for j = 1:length(vals)
test_X = [XX(i,j),YY(i,j)];
temp = 0;
for k=1:length(X)
temp = temp + a(k,1) * Y(k,1)*exp(-gamma*norm(X(k,:)-test_X)^2);
end
vals(i,j) = temp + B;
end
end
%%
figure
scatter(Data_x1(group1),Data_x2(group1),'.','r');
hold on
scatter(Data_x1(group2),Data_x2(group2),'*','b');
hold on
colormap bone;
contour(XX,YY,vals,[0 0],'LineWidth',2)
title(['\gamma = ',num2str(gamma)]);
end
%%
function K = get_kernel_matrix(data,gamma)
K = [];
for i=1:length(data)
for j=1:length(data)
K(i,j)=exp(-gamma*norm(data(i,:)-data(j,:))^2);
end
end
end
MySMO.m
function [alpha,bias] = MySMO(training_X,Labels,C,maxItertimes,tolerance)
% init
[sampleNum,featuerNum]=size(training_X);
alpha=zeros(sampleNum,1);
bias=0;
iteratorTimes=0;
K=training_X*training_X';%计算K
while iteratorTimestolerance)&&alpha(i,1)>0))
% choose j: different from i
j=i;
while j==i
j=randi(sampleNum);% 随机另外一个alpha2
end
alpha1=i;
alpha2=j;
% 更新alpha1 & alpha2
alpha_upd=alpha(alpha1,1);
alpha_upd=alpha(alpha2,1);
y1=Labels(alpha1,1);
y2=Labels(alpha2,1);
g2=(alpha.*Labels)'*(training_X*training_X(j,:)')+bias;
E2=g2-Labels(j,1);%计算error2
% 计算Lower & Higher
if y1~=y2
L=max(0,alpha_upd-alpha_upd);
H=min(C,C+alpha_upd-alpha_upd);
else
L=max(0,alpha_upd+alpha_upd-C);
H=min(C,alpha_upd+alpha_upd);
end
if L==H
fprintf('H==L\n');
continue;
end
parameter=K(alpha1,alpha1)+K(alpha2,alpha2)-2*K(alpha1,alpha2);
if parameter<=0
fprintf('parameter<=0\n');
continue;
end
% 得到新的alpha
alpha2New=alpha_upd+y2*(Error1-E2)/parameter;
if alpha2New>H
alpha2New=H;
end
if alpha2New0&&alpha1New0&&alpha2New a2New=L;
end
if abs(alpha2New-alpha_upd)<=0.0001
fprintf('change small\n');
continue;
end
alpha1New=alpha_upd+y1*y2*(alpha_upd-alpha2New);
% updata bias
bias1=-Error1-y1*K(alpha1,alpha1)*(alpha1New-alpha_upd)-y2*K(alpha2,alpha1)*(alpha2New-alpha_upd)+bias;
bias2=-E2-y1*K(alpha1,alpha2)*(alpha1New-alpha_upd)-y2*K(alpha2,alpha2)*(alpha2New-alpha_upd)+bias;
if alpha1New>0&&alpha1New0&&alpha2New end