白手起家学习数据科学 ——梯度下降法之“背后的思想”(六)

当我们做数据科学时，我们会频繁尝试找到在某种情况下最优的模型，通常”最好”的意思是”最小化模型误差”或者”最大化数据的可能性”。换句话说，它表示某些最优化问题的解决方案。

这个意思是我们需要解决一些最优化问题，尤其我们需要从头做起来解决他们，我们所使用的方法叫做梯度下降法(gradient descent)。你不可能发现它本身很惊艳，但是它能让我们做很惊艳的事情。

梯度下降法背后的思想(The Idea Behind Gradient Descent)

假设我们有函数f，输入参数为一个vector向量，输出为一个单值。一个这样简单的函数是：

def sum_of_squares(v):
    """computes the sum of squared elements in v"""
    return sum(v_i ** 2 for v_i in v)

我们需要最大化(最小化)这样的函数，即我们需要找到这样一个输入向量v，能产生最大(或者最小)的数值。

梯度(如果你记得微积分，这个就是不同变量偏导数的向量)提供给我们能够让函数很快变大的方向(如果你不记得微积分，根据我上面说的可以在网上查一查)。

最大化一个函数的方法是随机选取一个点，并计算其梯度，在梯度方向(这个方向引起函数变大)上走一小步，在新的开始点重复上面的步骤。类似的，你可以尝试在反方向走一些步最小化这个函数，如下图：

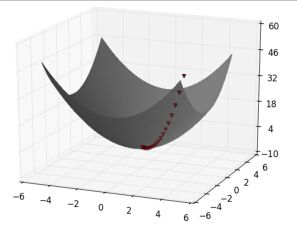
Notice:如果这个函数有唯一的全局最小值，那么这个步骤可能找到它。如果这个函数有多个(局部)最小值，这个步骤可能”找到”他们当中错误的一个，在这种情况下，你可以取不同的开始点重复运行这个步骤。如果一个函数没有最小值，那么这个步骤可能永远运行下去。

计算梯度(Estimating the Gradient)

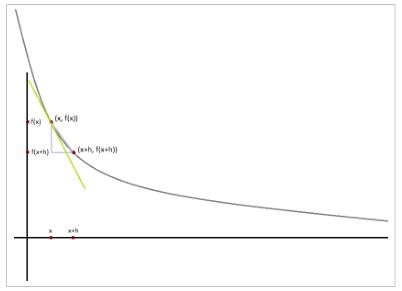
如果f是带一个变量的函数，它在x上的导数测量的是当x变化很小时 f(x) 怎样变化的，它被定义成差商(difference quotients):

def difference_quotient(f, x, h):
    return (f(x + h) - f(x)) / h

h接近于0。

导数是切线在 (x,f(x)) 上的斜率，而差商是 (x,f(x)) 与 (x+h,f(x+h)) 两点形成线( not-quite-tangent line)的斜率。当h变得越来越小时，not-quite-tangent line会越来越接近于在点 (x,f(x)) 上的切线。

很多函数很容易计算导数，例如，一个变量的平方函数：

def square(x):
    return x * x

有导数：

def derivative(x):
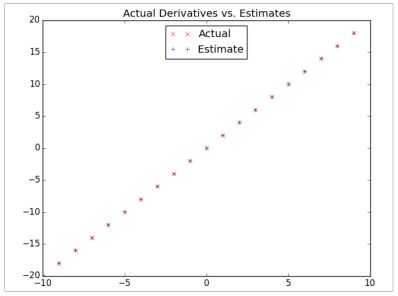
    return 2 * x

要是你不能(或者不想)计算梯度该怎么办？我们能通过具有很小的步长 e 的差商来计算导数，下图显示的评估效果：

derivative_estimate = partial(difference_quotient, square, h=0.00001)

# plot to show they're basically the same
import matplotlib.pyplot as plt
x = range(-10,10)
plt.title("Actual Derivatives vs. Estimates")
plt.plot(x, map(derivative, x), 'rx', label='Actual') # red x
plt.plot(x, map(derivative_estimate, x), 'b+', label='Estimate') # blue +
plt.legend(loc=9)
plt.show()

当f是一个具有多变量的函数，它有多个偏导数，每个变量小幅度变化时，是反应在对应偏导数上是怎样变化的。

我们计算出第 i 个变量的偏导数，把它看成是一个带有第i变量的函数，其他变量都看成常量：

def partial_difference_quotient(f, v, i, h):
    """compute the ith partial difference quotient of f at v"""
    w = [v_j + (h if j == i else 0) # add h to just the ith element of v
        for j, v_j in enumerate(v)]
    return (f(w) - f(v)) / h

使用相同方法计算出其他变量的梯度：

def estimate_gradient(f, v, h=0.00001):
    return [partial_difference_quotient(f, v, i, h)
        for i, _ in enumerate(v)]

Notice:使用差商法计算梯度主要的缺点是计算太耗时，如果v的长度是n，estimate_gradient的实际复杂度O(2n)，如果你重复计算梯度，你会花费更多的时间。

使用梯度(Using the Gradient)

很容易看出平方和(sum_of_squares)函数最小值是输入向量$v$都取0时，但是，假设我们不知道这个。让我们使用梯度下降法找到3个元素向量的最小值。我们会随机取一个开始点，然后计算梯度，取其反方向走微小的一步，直到获取梯度足够小的点。

def step(v, direction, step_size):
    """move step_size in the direction from v"""
    return [v_i + step_size * direction_i
        for v_i, direction_i in zip(v, direction)]

def sum_of_squares_gradient(v):
    return [2 * v_i for v_i in v]

# pick a random starting point
v = [random.randint(-10,10) for i in range(3)]

tolerance = 0.0000001

while True:
    gradient = sum_of_squares_gradient(v) # compute the gradient at v
    next_v = step(v, gradient, -0.01) # take a negative gradient step
    if distance(next_v, v) < tolerance: # stop if we're converging
        break
    v = next_v # continue if we're not

如果你运行这个，你最终会发现v是非常接近[0,0,0]，tolerance越小，v越接近[0,0,0]。

下一章节我们将要介绍如何优化梯度下降法的步长以及介绍随机梯度下降法(Stochastic Gradient Descent)。