Xgboost代码实现详解
目录
XGBOOST原理回顾
数据探索
数据预处理
构建简单的XGBoost 模型
Xgboost参数
XGBoost 参数调节
Step 1: 学习率与树个数
Step 2: 树的深度与节点权重
Step 3: 调节 gamma去降低过拟合风险
Step 4: 调节样本采样方式 subsample 和 colsample_bytree
Step 5: 减小学习率并增大树个数
【理论推导】 xgboost :提升树 XGBoost
【 代码】 Github : xgboost for Python, R, Java, Scala, C++ and more
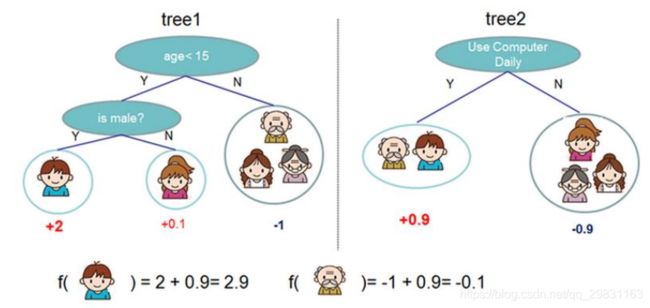
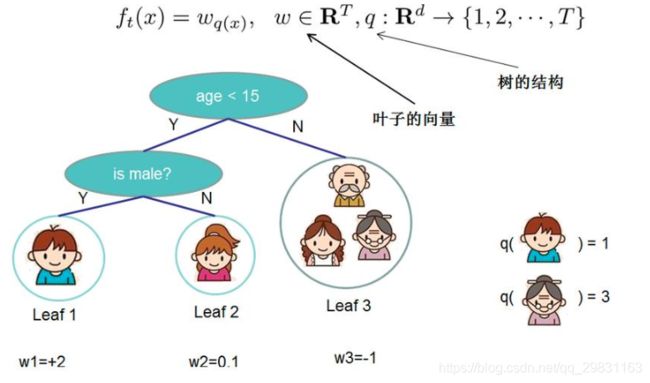
XGBOOST原理回顾
训练阶段:从给定的训练集构造出来一棵树(从跟节点开始选择特征, 如何进行特征切分)
测试阶段:根据构造出来的树模型从上到下去走一遍就好了
如何切分特征(选择节点): 根节点的选择该用哪个特征呢?接下来如何切分?
目标:通过一种衡量标准,来计算通过不同特征进行分支选择后的分类 情况,找出来最好的那个当成根节点,以此类推。
随机变量不确定性的度量: 熵;不确定性越大,熵值也就越大
如何决策一个节点的选择: 信息增益;表示特征X使得类Y的不确定性减少的程度。 (分类后的专一性,希望分类后的结果是同类在一起)
数据探索
偏度skew度量了实值随机变量的均值分布的不对称性。让我们计算损失的偏度:
stats.mstats.skew(train['loss']).data
# array(3.7949281496777445)skew 不等于3 则是确实倾斜的;对数据进行对数变换通常可以改善倾斜,可以使用 np.log
stats.mstats.skew(np.log(train['loss'])).data
# array(0.0929738049841997)通过绘制数值型特征的直方图来分析它们服从的分布;特征之间的相关性
train[cont_features].hist(bins=50, figsize=(16,12))
用热度图可视化特征之间的相关性
plt.subplots(figsize=(16,9))
correlation_mat = train[cont_features].corr() # 求相关系数矩阵
sns.heatmap(correlation_mat, annot=True) # 热度图; annot=True表示添加数值到图中
由此可以发现,相关程度大于0.8的特征有(cont1,cont9);(cont1,cont10);(cont6,cont9)(cont6,cont10);(cont6,cont13);(cont11,cont12)
数据预处理
#对数变换,使skew偏度接近3
train['log_loss'] = np.log(train['loss'])
# 数据分成连续和离散特征
features = [x for x in train.columns if x not in ['id','loss', 'log_loss']]
cat_features = [x for x in train.select_dtypes(
include=['object']).columns if x not in ['id','loss', 'log_loss']]
num_features = [x for x in train.select_dtypes(
exclude=['object']).columns if x not in ['id','loss', 'log_loss']]
print ("Categorical features:", len(cat_features)) # 类别型特征116
print ("Numerical features:", len(num_features)) # 数值型特征14
# 使用 一个标签来编码 categorical features:
ntrain = train.shape[0]
train_x = train[features]
train_y = train['log_loss']
for c in range(len(cat_features)):
train_x[cat_features[c]] = train_x[cat_features[c]].astype('category').cat.codes
print ("Xtrain:", train_x.shape) # Xtrain: (188318, 130)
print ("ytrain:", train_y.shape) # ytrain: (188318,)构建简单的XGBoost 模型
首先,我们训练一个基本的xgboost模型,然后进行参数调节通过交叉验证来观察结果的变换,使用平均绝对误差来衡量
mean_absolute_error(np.exp(y), np.exp(yhat))。
xgboost 自定义了一个数据矩阵类 DMatrix,会在训练开始时进行一遍预处理,从而提高之后每次迭代的效率
def xg_eval_mae(yhat, dtrain):
y = dtrain.get_label() # 之前对数据作了对数变换,所以现在要用np.exp(y)
return 'mae', mean_absolute_error(np.exp(y), np.exp(yhat)) # 平均绝对误差Xgboost参数
- 'booster':'gbtree',
- 'objective': 'multi:softmax', 多分类的问题
- 'num_class':10, 类别数,与 multisoftmax 并用
- 'gamma':0.1, 用于控制是否后剪枝的参数,越大越保守,一般0.1、0.2这样子。
- 'max_depth':12, 构建树的深度,越大越容易过拟合
- 'lambda':2, 控制模型复杂度的权重值的L2正则化项参数,参数越大,模型越不容易过拟合。
- 'subsample':0.7, 随机采样训练样本;取1.0时表示不随机采样
- 'colsample_bytree':0.7, 生成树时进行的列采样
- 'min_child_weight':3, 孩子节点中最小的样本权重和。如果一个叶子节点的样本权重和小于min_child_weight则拆分过程结束
- 'silent':0 ,设置成1则没有运行信息输出,最好是设置为0.
- 'eta': 0.007, 如同学习率
- 'seed':1000,随机数种子,使每次产生的随机数一样。
- 'nthread':7, cpu 线程数
xgb_params = {
'seed': 0,
'eta': 0.1,
'colsample_bytree': 0.5,
'silent': 1,
'subsample': 0.5,
'objective': 'reg:linear',
'max_depth': 5,
'min_child_weight': 3
}
%%time
# 使用交叉验证 xgb.cv
bst_cv1 = xgb.cv(xgb_params, dtrain, num_boost_round=50, nfold=3, seed=0,
feval=xg_eval_mae, maximize=False, early_stopping_rounds=10)
print ('CV score:', bst_cv1.iloc[-1,:]['test-mae-mean']) # CV score: 1220.229085
# 得到第一个基准结果:MAE=1220.2
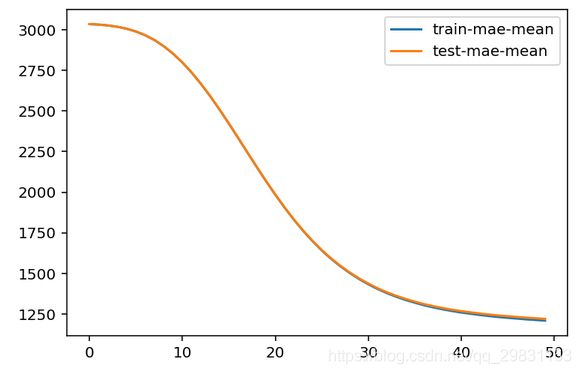
plt.figure() # 作损失函数的图
bst_cv1[['train-mae-mean', 'test-mae-mean']].plot()
第一个基础模型:没有发生过拟合 ;只建立了50个树模型.
%%time
#建立100个树模型
bst_cv2 = xgb.cv(xgb_params, dtrain, num_boost_round=100,
nfold=3, seed=0, feval=xg_eval_mae, maximize=False,
early_stopping_rounds=10)
print ('CV score:', bst_cv2.iloc[-1,:]['test-mae-mean']) # CV score: 1171.13663733
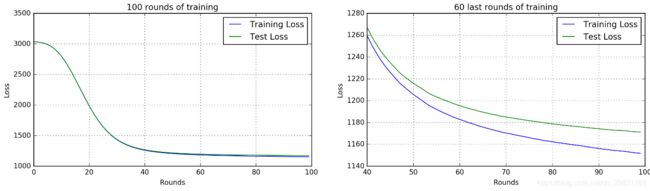
fig, (ax1, ax2) = plt.subplots(1,2)
fig.set_size_inches(16,4)
ax1.set_title('100 rounds of training')
ax1.set_xlabel('Rounds')
ax1.set_ylabel('Loss')
ax1.grid(True)
ax1.plot(bst_cv2[['train-mae-mean', 'test-mae-mean']])
ax1.legend(['Training Loss', 'Test Loss'])
ax2.set_title('60 last rounds of training')
ax2.set_xlabel('Rounds')
ax2.set_ylabel('Loss')
ax2.grid(True)
ax2.plot(bst_cv2.iloc[40:][['train-mae-mean', 'test-mae-mean']])
ax2.legend(['Training Loss', 'Test Loss'])有轻微的过拟合;新的MAE = 1171.77 比第一次的要好 (1218.9). 接下来我们要改变其他参数了。
XGBoost 参数调节
- Step 1: 选择一组初始参数
- Step 2: 改变
max_depth和min_child_weight.
- Step 3: 调节
gamma降低模型过拟合风险.
- Step 4: 调节
subsample和colsample_bytree改变数据采样策略.
- Step 5: 调节学习率
eta.
class XGBoostRegressor(object):
def __init__(self, **kwargs):
self.params = kwargs
if 'num_boost_round' in self.params:
self.num_boost_round = self.params['num_boost_round']
self.params.update({'silent': 1, 'objective': 'reg:linear', 'seed': 0})
def fit(self, x_train, y_train):
dtrain = xgb.DMatrix(x_train, y_train)
self.bst = xgb.train(params=self.params, dtrain=dtrain, num_boost_round=self.num_boost_round,
feval=xg_eval_mae, maximize=False)
def predict(self, x_pred):
dpred = xgb.DMatrix(x_pred)
return self.bst.predict(dpred)
def kfold(self, x_train, y_train, nfold=5):
dtrain = xgb.DMatrix(x_train, y_train)
cv_rounds = xgb.cv(params=self.params, dtrain=dtrain, num_boost_round=self.num_boost_round,
nfold=nfold, feval=xg_eval_mae, maximize=False, early_stopping_rounds=10)
return cv_rounds.iloc[-1,:]
def plot_feature_importances(self):
feat_imp = pd.Series(self.bst.get_fscore()).sort_values(ascending=False)
feat_imp.plot(title='Feature Importances')
plt.ylabel('Feature Importance Score')
def get_params(self, deep=True):
return self.params
def set_params(self, **params):
self.params.update(params)
return selfdef mae_score(y_true, y_pred): # loss函数为mae_score
return mean_absolute_error(np.exp(y_true), np.exp(y_pred))
# cross_validate可用make_scorer自定义损失函数
mae_scorer = make_scorer(mae_score, greater_is_better=False)
bst = XGBoostRegressor(eta=0.1, colsample_bytree=0.5, subsample=0.5,
max_depth=5, min_child_weight=3, num_boost_round=50)
bst.kfold(train_x, train_y, nfold=5)
'''
test-mae-mean 1219.014551
test-mae-std 8.931061
train-mae-mean 1210.682813
train-mae-std 2.798608
Name: 49, dtype: float64
'''Step 1: 学习率与树个数
Step 2: 树的深度与节点权重
这些参数对xgboost性能影响最大,因此,他们应该调整第一。我们简要地概述它们:
-
max_depth: 树的最大深度。增加这个值会使模型更加复杂,也容易出现过拟合,深度3-10是合理的。 -
min_child_weight: 正则化参数. 如果树分区中的实例权重小于定义的总和,则停止树构建过程。
xgb_param_grid = {'max_depth': list(range(4,9)), 'min_child_weight': list((1,3,6))}
xgb_param_grid['max_depth'] # [4, 5, 6, 7, 8]
%%time # 返回执行多条语句的时间
grid = GridSearchCV(XGBoostRegressor(eta=0.1, num_boost_round=50, colsample_bytree=0.5, subsample=0.5),
param_grid=xgb_param_grid, cv=5, scoring=mae_scorer)
grid.fit(train_x, train_y.values)
grid.grid_scores_, grid.best_params_, grid.best_score_网格搜索发现的最佳结果: {'max_depth': 8, 'min_child_weight': 6}, -1187.9597499123447);设置成负的值是因为要找大的值。
def convert_grid_scores(scores):
_params = []
_params_mae = []
for i in scores:
_params.append(i[0].values())
_params_mae.append(i[1])
params = np.array(_params)
grid_res = np.column_stack((_params,_params_mae))
return [grid_res[:,i] for i in range(grid_res.shape[1])]
_,scores = convert_grid_scores(grid.grid_scores_)
scores = scores.reshape(5,3)contourf(x,y,z)绘制三维图,并填充等高线之间的空隙颜色;其中前两个参数x和y为两个等长一维数组,第三个参数z为二维数组(表示平面点xi,yi映射的函数值)。由于contourf可以用颜色划分区域,常用于很多分类机器学习模型的可视化。
plt.figure(figsize=(10,5))
cp = plt.contourf(xgb_param_grid['min_child_weight'], xgb_param_grid['max_depth'], scores, cmap='BrBG')
plt.colorbar(cp)
plt.title('Depth / min_child_weight optimization')
plt.annotate('We use this', xy=(5.95, 7.95), xytext=(4, 7.5), arrowprops=dict(facecolor='white'), color='white')
plt.annotate('Good for depth=7', xy=(5.98, 7.05),
xytext=(4, 6.5), arrowprops=dict(facecolor='white'), color='white')
plt.xlabel('min_child_weight')
plt.ylabel('max_depth')
plt.grid(True)
plt.show()我们看到,从网格搜索的结果,分数的提高主要是基于max_depth增加. min_child_weight稍有影响的成绩,但是,我们看到,min_child_weight = 6会更好一些。
Step 3: 调节 gamma去降低过拟合风险
%%time
xgb_param_grid = {'gamma':[ 0.1 * i for i in range(0,5)]}
grid = GridSearchCV(XGBoostRegressor(eta=0.1, num_boost_round=50, max_depth=8, min_child_weight=6,
colsample_bytree=0.5, subsample=0.5),
param_grid=xgb_param_grid, cv=5, scoring=mae_scorer)
grid.fit(train_x, train_y.values)
grid.grid_scores_, grid.best_params_, grid.best_score_
# 我们选择使用偏小一些的 gamma.Step 4: 调节样本采样方式 subsample 和 colsample_bytree
%%time
xgb_param_grid = {'subsample':[ 0.1 * i for i in range(6,9)],
'colsample_bytree':[ 0.1 * i for i in range(6,9)]}
grid = GridSearchCV(XGBoostRegressor(eta=0.1, gamma=0.2, num_boost_round=50, max_depth=8, min_child_weight=6),
param_grid=xgb_param_grid, cv=5, scoring=mae_scorer)
grid.fit(train_x, train_y.values)
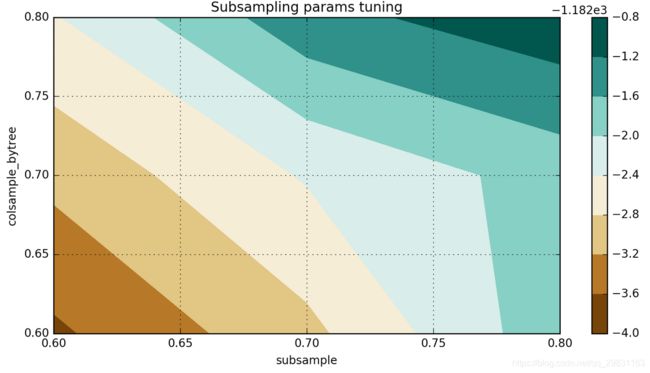
grid.grid_scores_, grid.best_params_, grid.best_score__, scores = convert_grid_scores(grid.grid_scores_)
scores = scores.reshape(3,3)
plt.figure(figsize=(10,5))
cp = plt.contourf(xgb_param_grid['subsample'], xgb_param_grid['colsample_bytree'], scores, cmap='BrBG')
plt.colorbar(cp)
plt.title('Subsampling params tuning')
plt.annotate('Optimum', xy=(0.895, 0.6), xytext=(0.8, 0.695), arrowprops=dict(facecolor='black'))
plt.xlabel('subsample')
plt.ylabel('colsample_bytree')
plt.grid(True)
plt.show()
在当前的预训练模式的具体案例,得到结果:`{'colsample_bytree': 0.8, 'subsample': 0.8}, -1182.9309918891634)
Step 5: 减小学习率并增大树个数
参数优化的最后一步是降低学习速度,同时增加更多的估计量
先对一个简单点的(有50 棵树)模型,作出不同学习率的图。
%%time
xgb_param_grid = {'eta':[0.5,0.4,0.3,0.2,0.1,0.075,0.05,0.04,0.03]}
grid = GridSearchCV(XGBoostRegressor(num_boost_round=50, gamma=0.2, max_depth=8, min_child_weight=6,
colsample_bytree=0.6, subsample=0.9),
param_grid=xgb_param_grid, cv=5, scoring=mae_scorer)
grid.fit(train_x, train_y.values)
grid.grid_scores_, grid.best_params_, grid.best_score_eta, y = convert_grid_scores(grid.grid_scores_)
plt.figure(figsize=(10,4))
plt.title('MAE and ETA, 50 trees')
plt.xlabel('eta')
plt.ylabel('score')
plt.plot(eta, -y)
plt.grid(True)
plt.show(){'eta': 0.2}, -1160.9736284869114 是目前的模型最好的结果;现在我们把树的个数增加到100。
xgb_param_grid = {'eta':[0.5,0.4,0.3,0.2,0.1,0.075,0.05,0.04,0.03]}
grid = GridSearchCV(XGBoostRegressor(num_boost_round=100, gamma=0.2, max_depth=8, min_child_weight=6,
colsample_bytree=0.6, subsample=0.9),
param_grid=xgb_param_grid, cv=5, scoring=mae_scorer)
grid.fit(train_x, train_y.values)
grid.grid_scores_, grid.best_params_, grid.best_score_ # {'eta': 0.1}, -1152.2471498726127)
eta, y = convert_grid_scores(grid.grid_scores_)
plt.figure(figsize=(10,4))
plt.title('MAE and ETA, 100 trees')
plt.xlabel('eta')
plt.ylabel('score')
plt.plot(eta, -y)
plt.grid(True)
plt.show()学习率低一些的效果更好;
%%time
# 把树的数目增加到200,找出最优的学习率
xgb_param_grid = {'eta':[0.09,0.08,0.07,0.06,0.05,0.04]}
grid = GridSearchCV(XGBoostRegressor(num_boost_round=200, gamma=0.2, max_depth=8, min_child_weight=6,
colsample_bytree=0.6, subsample=0.9),
param_grid=xgb_param_grid, cv=5, scoring=mae_scorer)
grid.fit(train_x, train_y.values)
grid.grid_scores_, grid.best_params_, grid.best_score_ # {'eta': 0.07},
-1145.9235944370419)
eta, y = convert_grid_scores(grid.grid_scores_)
plt.figure(figsize=(10,4))
plt.title('MAE and ETA, 200 trees')
plt.xlabel('eta')
plt.ylabel('score')
plt.plot(eta, -y)
plt.grid(True)
plt.show()最终的模型参数
%%time
# Final XGBoost model
bst = XGBoostRegressor(num_boost_round=200, eta=0.07, gamma=0.2, max_depth=8, min_child_weight=6,
colsample_bytree=0.6, subsample=0.9)
cv = bst.kfold(train_x, train_y, nfold=5)
cv
'''
test-mae-mean 1146.997852
test-mae-std 9.541592
train-mae-mean 1036.557251
train-mae-std 0.974437
Name: 199, dtype: float64
'''我们看到200棵树最好的ETA是0.07。正如我们所预料的那样,ETA和num_boost_round依赖关系不是线性的,但是有些关联。优化xgboost 从初始值: 1219.57. 经过调参之后达到 MAE=1171.77. 发现参数之间的关系ETA和num_boost_round:
- 100 trees,
eta=0.1: MAE=1152.247 - 200 trees,
eta=0.07: MAE=1145.92
XGBoostRegressor(num_boost_round=200, gamma=0.2, max_depth=8, min_child_weight=6, colsample_bytree=0.6, subsample=0.9, eta=0.07).补充:
early stop :在训练xgboost时,若连续几个epoch的训练,loss值都没有下降,则提前终止训练。
verbose = True 则显示每增加一个模型后loss值得变化。
plot_importance(model) 可显示model中各个特征得重要程度,便于对比特征;
网格搜索 GridSearchCV.