【ECCV2020】Spatio-Temporal Graph Transformer Networks for Pedestrian Trajectory Prediction

【ECCV2020】用于行人轨迹预测的时空图 Transformer 网络

摘要

       了解人群运动动力学对于现实世界的应用至关重要，例如监控系统和自动驾驶。这是具有挑战性的，因为它需要对具有社会意识的人群空间交互和复杂的时间依赖性进行有效建模。我们认为注意力是轨迹预测的最重要因素。在本文中，我们提出了 STAR，这是一个时空图 tRans-former 框架，它仅通过注意机制来处理轨迹预测。 STAR 通过 TGConv 对图内人群交互进行建模，TGConv 是一种基于 Transformer 的新型图卷积机制。图间时间依赖性由单独的时间转换器建模。 STAR 通过在空间和时间转换器之间交错来捕获复杂的时空交互。为了校准对消失的行人的长期影响的时间预测，我们引入了一个可读写的外部存储模块，由时间转换器持续更新。我们表明，仅通过注意力机制，STAR 在 5 个常用的现实世界行人预测数据集上实现了最先进的性能。
关键词： 轨迹预测、Transformer、图神经网络

1 引言

       人群轨迹预测对于计算机视觉和机器人community都至关重要。 这项任务具有挑战性，因为 1) 人与人之间的互动是多模式的，而且极难捕捉，例如，陌生人会避免与他人亲密接触，而同伴则倾向于成群结队地行走； 2）复杂的时间预测与空间人与人的交互相结合，例如，人类根据相邻的人的历史和未来运动来调节他们的运动。
       经典模型通过手工制作的能量函数捕捉人与人的交互，这需要大量的特征工程工作，并且通常无法在拥挤的空间中建立人群交互。随着深度神经网络的最新进展，循环神经网络 (RNN) 已广泛应用于轨迹预测并表现出良好的性能。基于 RNN 的方法通过潜在状态捕捉行人运动，并通过合并空间邻近行人的潜在状态来模拟人与人的交互。 Social-pooling 平等对待邻里区域的行人，并通过池化机制合并他们的潜在状态。注意力机制放宽了这一假设，并根据学习到的函数对行人进行加权，该函数编码了相邻行人对于轨迹预测的不平等重要性。然而，现有的预测器有两个共同的局限性：1) 使用的注意力机制仍然很简单，无法完全模拟人与人的交互，2) RNN 通常难以对复杂的时间依赖性进行建模。
       近年来，Transformer网络在自然语言处理领域取得了突破性的进展。Transformer摒弃了语言序列的顺序性和模型时间依赖性，只使用强大的注意力机制。Transformer架构的主要好处是，与 RNN 相比，注意力机制显著改善了时间建模，特别是对于水平序列。然而，基于transformer的模型仅限于正常的数据序列，很难推广到更多的结构化数据，例如 图序列。

       在本文中，我们介绍了时空图transformer（STAR）框架，这是一种完全基于自注意力机制的时空轨迹预测新框架。我们相信学习时间、空间和时空注意力是准确预测人群轨迹的关键，而 Transformers 为这项任务提供了一种简洁有效的解决方案。 STAR 使用新颖的空间图 Transformer 捕捉人与人的交互。特别是，我们引入了 TGConv，一种基于 Transformer 的图卷积机制。 TGConv 通过 Transformers 的自注意力机制改进了基于注意力的图卷积，可以捕捉更复杂的社交互动。具体来说，TGConv 倾向于在行人密度较高的数据集（ZARA1、ZARA2、UNIV）上改进更多。我们使用单独的时间 Transformer 对行人运动进行建模，与 RNN 相比，它可以更好地捕捉时间依赖性。 STAR 通过在空间 Transformer 和时间 Transformer 之间进行交错来提取行人之间的时空交互，这是一种简单而有效的策略。此外，由于 Transformers 将序列视为一组词，因此它们通常在对时间序列数据进行建模时遇到问题，其中强制执行强时间一致性。我们引入了一个额外的可读写图形内存模块，它在预测期间连续对嵌入执行平滑。图 2.(b) 给出了 STAR 的概述。

       我们在5个常用的真实行人轨迹预测数据集上进行了实验。只有关注机制，STAR在所有5个数据集上都达到了最先进的水平。我们进行了广泛的消融研究，以更好地理解每个提出的成分。

2 背景

2.1 自注意力机制和 Transformer 网络

       Transformer网络在NLP领域取得了巨大的成功，如机器翻译、情感分析、文本生成等。Transformer网络遵循RNNseq2seq模型中广泛使用的著名 编码器-解码器结构。
        Transformer 的核心思想是通过多头自注意力机制来完全复发。对于嵌入$\{h_t{\}}_{t=1}^T$，Transformers 的自注意首先学习 t = 1 到 T 的所有嵌入的 Query 矩阵 $Q=f_Q(\{h_t{\}}_{t=1}^T)$，key 矩阵 $K=f_K(\{h_t{\}}_{t=1}^T)$ 和对应的 value 矩阵 $V=f_V(\{h_t{\}}_{t=1}^T)$ ，然后用
$$\begin{array}{r}Att(Q,K,V)=\frac{Softmax(Q{K}^T)}{\sqrt{d_k}}\end{array}\text{\hspace{1em}(1)}$$计算每个查询的注意，其中 $d_k$ 为每个查询的维数。
       $1/\sqrt{d_k}$ 实现了缩放点乘积项，用于注意力的数值稳定性。通过计算跨不同时间步长的嵌入之间的自注意力，自注意力机制能够在较长时间范围内学习时间依赖项，这与使用有限内存的单个向量记忆历史的RNN不同。此外，将注意力解耦到查询、键和值元组中允许自注意力机制捕获更复杂的时间依赖。
       多头注意机制在计算注意时学会了将多个假设结合起来。它允许模型在不同的位置共同关注来自不同表征的信息。对于 $k$ 个头，我们有
$$\begin{array}{r}MultiHead(Q,K,V)=f_O([hea{d}_i{]}_{i=1}^k)\end{array}\text{\hspace{1em}(2)}$$
$$\begin{array}{r}wherehea{d}_i=At{t}_i(Q,K,V)\end{array}$$
，其中fO是一个全连接层，融合了k个头的输出，$At{t}_i(Q,K,V)$ 表示第 i 个头的自注意力。附加位置编码用于在 Transformer 嵌入中添加位置信息。最后，Transformer 通过两个跳过连接的全连接层输出更新的嵌入。
       然而，目前基于Transformer的模型的一个主要局限是只适用于非结构化的数据序列，如词序列。STAR将Transformers扩展到更结构化的数据序列，作为第一步，图序列，并将其应用于轨迹预测。

2.2 相关工作

       图神经网络。图神经网络( Graph Neural Networks，GNNs )是一种强大的图结构数据深度学习结构。图卷积在图机器学习任务上表现出了显著的改进，如物理系统建模、药物预测和社会推荐系统。特别地，图注意力网络( Graph Attention Networks，GAT ) 实现了节点间高效的加权消息传递，并取得了跨多个领域的最新成果。从序列预测的角度看，时序图 RNNs 允许在图序列中学习时空关系。我们的 STAR 利用 Transformer TGConv改进了GAT，它提高了注意力机制，解决了 Transformer 结构的图形时空建模问题。
       序列预测。RNNs及其变体，如LSTM 和GRU ，在序列预测任务中取得了巨大成功，如语音识别、机器人定位、机器人决策等。RNNs 也被成功应用于行人的时间运动模式建模。基于 RNNs 的预测器使用 Seq2Seq 结构进行预测。附加的结构，例如，社会池化，注意力机制和图神经网络，用于改进轨迹预测与社会交互建模。
       近年来，Transformer 网络在自然语言处理领域占据主导地位。Transformer 模型完全抛弃了递归并将注意力集中在跨时间步骤上。这种架构允许长期依赖建模和大批量并行训练。Transformer 架构也被成功应用于其他领域，例如股票预测、机器人决策等。STAR 将 Transformer 的思想应用于图形序列。我们在一个具有挑战性的人群轨迹预测任务上演示它，其中我们将人群交互视为一个图形。STAR 是一个通用框架，可以应用于其他图序列预测任务，例如社交网络中的事件预测和物理系统建模。我们把这个留给以后学习。
       人群交互建模。作为开创性的工作，社会力量模型已被证明在各种应用中有效，例如人群分析和机器人。他们假设行人在虚拟力的驱动下进行目标导航和避碰。社会力模型在交互建模方面工作良好，在轨迹预测方面表现不佳。基于几何的方法，如ORCA 和PORCA ，考虑Agent的几何结构，将交互建模转化为优化问题。经典方法的一个主要局限在于它们依赖于手工制作的特征，这些特征非常容易调整，难以概括。
       基于深度学习的模型通过直接从数据中学习模型来实现自动特征工程。行为CNNs 通过CNNs捕捉人群互动。社交聚合( Social-Pooling )通过近似人群交互的聚合机制进一步编码近端行人状态。最近的研究将人群视为一个图，将空间邻近行人的信息与注意机制进行合并。与池化方法相比，注意机制对行人进行重要建模。图神经网络也被应用于寻址人群建模。显式消息传递使得网络能够对更复杂的社会行为建模。

3 方法

3.1 综述

       在本节中，我们介绍了提出的基于时空图 Transformer 的轨迹预测框架 STAR。我们认为注意力是有效和高效的轨迹预测的最重要因素。
       STAR。将时空注意力建模分解为时间建模和空间建模。对于时间建模，STAR 独立地考虑每个行人，并应用标准的时间转换网络来提取时间依赖项。与RNNs相比，时态变换提供了更好的时态依赖建模协议，我们在烧蚀研究中验证了这一点。对于空间建模，我们引入了基于 Transformer 的消息传递图卷积机制TGConv。TGConv以更好的注意机制改进了目前的图卷积方法，为复杂的空间相互作用给出了更好的模型。特别是，TGConv更倾向于在行人密度较高(ZARA1、ZARA2、UNIV)和复杂交互的数据集上改进。我们构造了两个编码器模块，每个模块包含一对时空变换，并将其叠加，提取时空交互。

3.2 问题设置

       考虑到在时间步长 1 到 $T_{obs}$ 过程中观察到的历史，我们感兴趣的问题是预测一个场景中总共 N 个行人从时间步长 $T_{obs}+1$ 到 T 的未来轨迹。在每个时间步长 t，我们有一组 N 个行人 $\{p_t^i{\}}_{i=1}^N$，其中 $p_t^i=(x_t^i,y_t^i)$ 表示行人在自顶向下视图映射中的位置。我们假设距离小于 d 的行人对 $(p_t^i,p_t^i)$ 有一个无向边 $(i,j)$。这就导致在每个时间步长t处有一个交互图：$G_t=(V_t,E_t)$，其中 $V_t=\{p_t^i{\}}_{i=1}^N$ 且 $Et=\{(i,j)|i,j在时间t处连通\}$。对于 t 时刻的每个节点 i，定义其邻接集为$Nb(i,t)$，其中对于每个节点$j\in Nb(i,t)，et(i,j)\in E_t$。

3.3 时间Transformer

       STAR 中的时间 Transformer 块使用一组行人轨迹嵌入 $\{h_1^i{\}}_{i=1}^N,\{h_2^i{\}}_{i=1}^N,...,\{h_t^i{\}}_{i=1}^N$ 作为输入，并输出一组具有时间依赖关系的更新嵌入 $\{{h^{\prime }}_1^i{\}}_{i=1}^N,\{{h^{\prime }}_2^i{\}}_{i=1}^N,...,\{{h^{\prime }}_t^i{\}}_{i=1}^N$ 作为输出，独立考虑每个行人。
       图 3 给出了时序 Transformer 块的结构。( a ) 自注意力块首先学习给定输入的查询矩阵 $\{Q^i{\}}_{i=1}^N$，密钥矩阵 $\{K^i{\}}_{i=1}^N$ 和值矩阵 $\{V^i{\}}_{i=1}^N$。对于行人，我们有
$$\begin{array}{r}{Q}^i=f_Q(\{h_j^i{\}}_{j=1}^t),K^i=f_K(\{h_j^i{\}}_{j=1}^t),V^i=f_V(\{h_j^i{\}}_{j=1}^t)\end{array}\text{\hspace{1em}(3)}$$其中，$f_Q$、$f_K$和 $f_V$ 是行人 $i=1,\dots ,N$ 共享的相应查询、密钥和值函数。我们可以利用GPU的加速实现所有行人的并行计算。

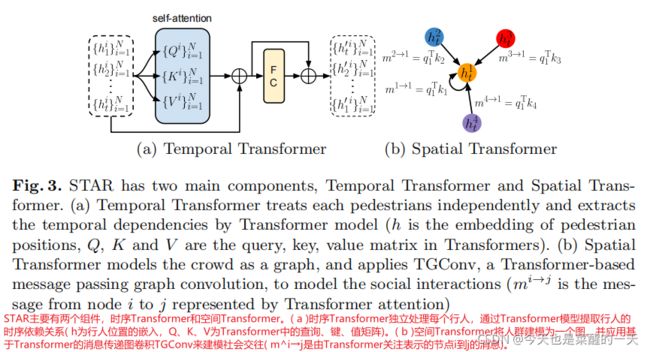
       我们按照Eq1分别计算每个行人的注意力。类似地，我们将行人i的多头注意力( k头)表示为
$$\begin{array}{r}Att(Q^i,K^i,V^i)=\frac{Softmax(Q^i{K}^{iT})}{\sqrt{d_k}}{V}^i\end{array}\text{\hspace{1em}(4)}$$
$$\begin{array}{r}MultiHead(Q^i,K^i,V^i)=f_O([hea{d}_j{]}_{j=1}^k)\end{array}\text{\hspace{1em}(5)}$$
$$\begin{array}{r}wherehea{d}_j=Att(Q^i,K^i,V^i)\end{array}\text{\hspace{1em}(6)}$$
       其中 $f_O$ 是一个全连接层，它合并了 k 个头部，$At{t}_j$ 索引了第 j 个头部。最终的嵌入由两个跳跃连接和一个最终的全连接层生成，如图 3(a) 所示。
       时间Transformer是Transformer网络对数据序列集的简单推广。我们在实验中论证了基于Transformer的体系结构提供了更好的时间建模。

3.4 空间Transformer

       空间Transformer块提取行人之间的空间交互。我们提出了一种新的基于Transformer的图卷积，TGConv用于图上的消息传递。
       我们的关键观察是，自注意力机制可以被视为无向全连接图上的消息传递。对于特征集 $\{h_i{\}}_{i=1}^n$ 的一个特征向量 $h_i$，我们可以将其对应的查询向量表示为 $q_i=f_Q(h_i)$，键向量表示为 $k_i=f_K(h_i)$，值向量表示为 $v_i=f_V(h_i)$。我们将全连通图中从节点 $j$ 到 $i$ 的消息定义为
$$\begin{array}{r}{m}^{j\to i}=q_i^T{k}_j\end{array}\text{\hspace{1em}(7)}$$注意力函数( Eq.1 )可以改写为
$$\begin{array}{r}Att(Q^i,K^i,V^i)=\frac{Softmax([m^{j\to i}{]}_{i,j=1:n})}{\sqrt{d_k}}[v_i{]}_{i=1}^n\end{array}\text{\hspace{1em}(8)}$$
       基于上述见解，我们引入了基于 Transformer 的图卷积( TGConv )。TGConv 本质上是一种基于注意力的图卷积机制，与 GATConv 类似，但具有更好的 Transformers 驱动的注意力机制。对于任意图 $G=(V,E)$，其中 $V=\{1，2，..，n\}$ 是节点集，$E=\{(i,j)|i，j是连通的\}$。假设每个节点 $i$ 与一个嵌入 $h_i$ 和一个邻居集合 $Nb(i)$ 相关联。节点i的图卷积操作写为

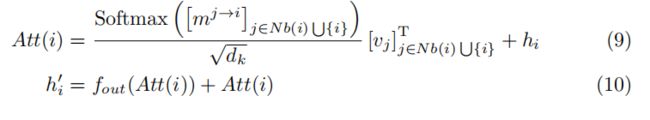
其中 $f_{out}$ 是输出函数，在我们的实验情况下，是一个完全连接的层，${h^{\prime }}_i$ 是 TGConv 对节点 $i$ 的更新嵌入。我们通过$TGConv(h_i)$ 总结节点 $i$ 的 TGConv 函数。在 Transformer 结构中，我们通常在上述方程中的每一个跳过连接后都会应用层归一化(normalization)。我们在方程中忽略了它们，以得到一个整洁的符号。
       空间 Transformer，如图 3(b) 所示，可以方便地由 TGConv 实现。对每个图 $G_t$ 分别施加一个具有共享权重的 TGConv。我们认为 TGConv 是通用的，可以应用于其他任务，我们将它留给未来的研究。

3.5 时空图Transformer

       在这一部分中，我们介绍了用于行人轨迹预测的时空图 Transformer ( STAR ) 框架。
       时间 Transformer 可以单独对每个行人的运动动力学进行建模，但未能纳入空间相互作用；空间 Transformer 处理与 TGConv 的人群交互，但很难推广到时间序列。行人预测的一个主要挑战是建立耦合时空相互作用模型。行人的时空动态是紧紧相依的。例如，当一个人决定她的下一个动作时，首先要预测她的邻居的未来动作，并选择一个在一个时间间隔 Δt 内避免与他人碰撞的动作。
       STAR通过将时空 Transformer 交织在一个单一的框架，解决耦合时空建模问题。图 4 给出了 STAR 的网络结构。STAR 有两个编码器模块和一个简单的解码器模块。网络的输入为 $t=1$ 到 $t=T_{obs}$ 的行人位置序列，其中t时刻的行人位置用 $\{p_t^i{\}}_{i=1}^N$ 表示，$p_t^i=(x_t^i，y_t^i)$。在第一个编码器中，通过两个独立的全连接层对位置进行嵌入，并将嵌入传递给空间 Transformer 和时间 Transformer，从行人历史中提取独立的时空信息。然后，空间和时间特征被一个全连接层合并，它提供了一组具有时空编码的新特征。为了进一步对特征空间中的时空交互进行建模，我们使用第二编码器模块对特征进行后处理。在编码器2中，空间 Transformer 利用时间信息建模空间交互；时间 Transformer 增强了输出的空间嵌入性，具有时态注意力。STAR 通过一个简单的全连接层来预测行人在 $t=T_{obs}+1$ 时刻的位置，该层以第二个时间 Transformer 的 $t=T_{obs}$ 嵌入为输入，与随机高斯噪声相连接，产生各种未来预测。我们根据预测位置连接距离小于d的节点构造 $G_{T_{obs}}+1$。将预测加入到历史中进行下一步预测。
       与结合时空 Transformer 相比，STAR架构显著提高了时空建模能力。

3.6 外部图形存储器

       尽管 Transformer 网络通过自注意机制改进了长视距序列建模，但它可能难以处理需要强时间一致性的连续时间序列数据。然而，时间一致性是轨迹预测的严格要求，因为行人位置通常在短时间内不会发生剧烈变化。
       我们引入一个简单的外部图形内存来解决这个难题。图存储器 $M_{1:T}$ 是可读可写可学习的，其中 $M_t(i)$ 与 $h_t^i$ 具有相同的大小并记忆行人 i 的嵌入。在时间步长 t，在编码器 1 中，时序 Transformer 首先从内存 M 中读取过去的图嵌入函数 $\{h_1^i,h_2^i,...,h_{t-1}^i{\}}_{i=1}^N=f_{read}(M)$ ，并将其与当前的图嵌入函数 $\{h_t^i{\}}_{i=1}^N$ 拼接起来。这允许时序 Transformer 在上一个嵌入上设置当前嵌入以实现一致预测。在编码器 2 中，我们通过函数 $M^{\prime }=f_{write}(\{{h^{\prime }}_1^i,{h^{\prime }}_2^i,...,{h^{\prime }}_t^i{\}}_{i=1}^N,M)$ 将时序 Transformer 的输出 $\{{h^{\prime }}_1^i,{h^{\prime }}_2^i,...,{h^{\prime }}_t^i{\}}_{i=1}^N$ 写入到图存储器中，它对时间序列数据执行平滑操作。对于任何 $t^{\prime }<t$ ，嵌入将由 ${t^{\prime }}^{\prime }>t$的信息更新，从而为更一致的轨迹赋予时间平滑的嵌入。
       为了实现 $f_{read}$ 和 $f_{write}$，可以采用许多潜在的函数形式。在本文中，我们只考虑一个非常简单的策略

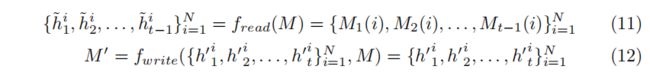
也就是说，我们直接用嵌入替换内存，并复制内存生成输出。这种简单的策略在实践中效果良好。可以考虑更复杂的 $f_{read}$ 和 $f_{write}$ 的功能形式，如全连接层或 RNNs 。我们把这个留给未来的研究。

4 实验

       在本节中，我们首先报告了作为轨迹预测任务的主要基准的五个行人轨迹数据集的结果：ETH ( ETH和HOTEL )和UCY ( ZARA1、 ZARA2和 UNIV )数据集。我们将STAR与9个轨迹预测器进行比较，包括SOTA模型、SR - LSTM 。我们遵循先前工作中普遍采用的留一交叉验证评估策略。我们还进行了广泛的消融研究，以了解每个建议成分的效果，并试图在轨迹预测任务中为模型设计提供更深入的见解。
       作为一个简单的结论，我们表明：1 )在5个数据集上，STAR在4个数据集上优于SOTA模型，并且在其他数据集上具有与SOTA模型相当的性能；2 )与现有的图卷积方法相比，空间 Transformer 改进了人群交互建模；3 )时序 Transformer 正常地改进LSTM；4 )图形内存提供了更平滑的时间预测和更好的性能。

4.1 实验设置

       对于我们的方法，我们遵循与SR-LSTM 相同的数据预处理策略。所有输入的原点都转移到最后一个观测帧。采用随机旋转进行数据增强。
       —— 平均位移误差( ADE )：预测轨迹和地面实际轨迹的总体估计位置的均方误差( MSE )。
       —— 最终位移误差( FDE )：预测最终目的地和地面实际最终目的地之间的距离。
       我们将8帧( 3.2s )作为一个序列，12帧( 4.8s )作为预测的目标序列，以便与所有现有的工作进行公平的比较。

4.2 实现细节

       作为输入的坐标首先被完全连接的层编码成32大小的向量，然后再进行ReLU激活。在处理输入数据时，采用0.1的 dropout。所有 Transformer 层均接受特征尺寸为32的输入。空间 Transformer 和时间 Transformer 均由8个头的编码层组成。我们对学习率进行了超参数搜索，从 0.0001 到 0.004，间隔 0.0001 在一个较小的网络上，选择性能最好的学习率( 0.0015 )来训练其他所有模型。因此，我们使用学习率为 0.0015、批大小为 16 的 Adam 优化器对网络进行 300 个 epoch 的训练。每个批包含 256 名左右的行人，在不同的时间窗口，由 attention mask 指示，以加速训练和推理过程。

4.3 基线

我们将STAR与广泛的基线进行比较，包括：
1）LR：一个简单的时态线性回归器。
2）LSTM：一个普通的时间性LSTM。
3）S-LSTM[1]：每个行人都用LSTM建模，每个时间步长的隐藏状态都与邻居汇集。
4）Social Attention[45]：它将人群建模为一个时空图，并使用两个LSTM来捕捉空间和时间的动态。
5）CIDNN[49]：用LSTMs进行时空人群轨迹预测的模块化方法。
6）SGAN[16]：一个使用GANs的随机轨迹预测器。
7）SoPhie[40]：SOTA的随机轨迹预测器之一，采用LSTMs。
8）TrafficPredict [38]。基于LSTM的异质交通代理的运动预测器。请注意，[38]中的TrafficPredict报告了等比例的归一化结果。为了进行一致的比较，我们将其缩减。
9）SR-LSTM：具有运动门和成对关注的SOTA轨迹预测器，以完善LSTM编码的隐藏状态，获得社会互动。

4.4 定量结果和分析

       我们将 STAR 与第 4 节中提到的最先进的方法进行比较。4.3 所有的随机方法采样 20 次，并报告表现最好的样本。
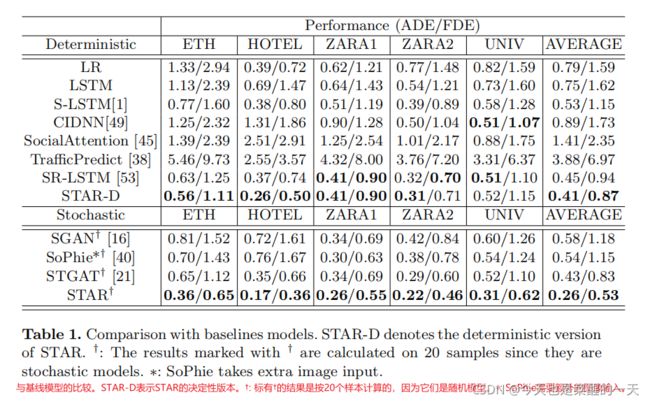
       主要结果列于表 1。我们观察到，STAR-D 在整体性能上优于 SOTA 的确定性模型，而随机的 STAR 在很大程度上超过了所有 SOTA 模型。
       一个有趣的发现是，简单模型 LR 的性能明显优于许多深度学习方法，包括 SOTA 模型、SR-LSTM，在酒店场景，其中大部分包含直线轨迹，而且相对来说 不太拥挤。这表明，这些复杂的模型可能适用于那些复杂的场景，如 UNIV。另一个例子是，STAR在 ETH 和 HOTEL 上的表现明显优于 SR-LSTM，但在 UNIV 上只与 SR-LSTM 相当。在人群密度很高的 UNIV 上，STAR 的表现明显优于 SR-LSTM。这有可能是由于 SR-LSTM 有一个精心设计的门控结构，用于图上的信息传递，但其时间性相对较弱。图上的消息传递，但有一个相对较弱的时间模型，即一个 LSTM。SR-LSTM 的设计 SR-LSTM的设计有可能改善空间建模，但也可能导致过拟合。相比之下，我们的方法在简单和复杂场景中都表现良好。然后，我们将在第4.5节中用可视化的结果进一步证明这一点。4.5节中用可视化的结果进一步证明。

4.5 定性结果和分析

       我们在图 5 和图 6 中介绍了我们的定性结果。
       —— STAR能够预测时间上一致的轨迹。在图5.（a）中。STAR成功地捕获了单一行人的意图和速度，其中不存在社会互动。
       —— STAR 成功地提取了人群的社会互动。我们在图 6 中可视化了第二个空间 Transformer 的注意值。我们注意到，行人对自己和可能与他们相撞的邻居给予了高度关注。例如，图6.©和(d)；对空间上较远的行人和没有意图冲突的行人的注意较少，例如，图6.(a)和(b)。
       —— STAR 能够捕捉到人群的时空互动。在图5.(b)中。我们可以看到，对行人的预测考虑了他们邻居的未来运动 他们的邻居的未来运动。此外，与 SR-LSTM 相比，STAR 更好地平衡了空间建模和时间建模。SR-LSTM 有可能在空间建模方面可能会过拟合，并且经常倾向于预测曲线，即使是在行人直行的时候。行人是直线行走的。这也与我们在定量分析部分的发现相吻合。定量分析部分的发现，即深度预测器对复杂数据集的过度适应。STAR通过空间-时间 Transformer 结构更好地缓解了这个问题。
       ——为了更准确地进行轨迹预测，需要辅助信息。虽然STAR实现了SOTA的结果，但预测偶尔还是会不准确，例如，图5.(d)。行人走了一个急转弯，这使得我们不可能纯粹根据历史上的位置来预测未来的轨迹。对于未来的工作，应该使用额外的信息，如环境设置或地图，为预测提供额外的信息。

4.6 消融研究

       我们对所有5个数据集进行了广泛的消融研究，以了解每个STAR组件的影响。具体来说，我们选择确定性的STAR，以消除随机样本的影响，并集中研究所提出的组件的影响。结果列于表2。
       —— 与RNNs相比，时序 Transformer 改善了对行人动态的时间建模。在(4)和(5)中，我们删除了图形记忆，并固定了空间编码的STAR。（4）的LSTM和（5）的STAR，这两个模型的时间预测能力只取决于它们的时间编码器。我们观察到，具有时间 Transformer 编码的模型在整体性能上优于 LSTM，这表明 Transformer 与 RNN 相比提供了更好的时间建模能力。
       —— TGConv在人群运动建模上优于其他图卷积方法。在（1）、（2）、（3）和（7）中，我们改变了空间编码器，并将TGConv（7）的空间 Transformer 与 GCN[24]、GATConv[44] 和多头加性图卷积[5]进行比较。我们观察到，在人群建模的情况下，TGConv 与其他两个基于注意力的图卷积相比，取得了更高的性能增益。
       —— 交错的空间和时间 Transformer 能够更好地提取时空相关性。在(6)和(7)中，我们观察到在 STAR 框架中提出的两个编码器结构(7)，普遍优于单 编码器结构（6）。这种经验上的性能增益可能表明空间和时间 Transformer 的交错能够提取出更复杂的行人的时空互动。
       —— 图式记忆给出了一个更平滑的时间嵌入，并提高了性能。在（5）和（7）中，我们验证了图记忆模块的嵌入平滑能力，其中（5）是没有GM的STAR变体。我们首先注意到，图记忆在所有的数据集上都提高了STAR的性能。此外，我们注意到，在ZARA1上，空间交互很简单，时间一致性预测更重要，图记忆以最大的幅度改善了（6）到（7）。根据经验证据，我们可以得出结论，图记忆的嵌入平滑能够改善STAR的整体时间建模。

5 结论

       我们介绍了STAR，一个只用注意力机制进行时空人群轨迹预测的框架。STAR由两个编码器模块组成，由空间Transformer和时间Transformer组成。我们还引入了TGConv，一个新的强大的基于Transformer的图卷积机制。只用注意力机制的STAR在5个常用的数据集上实现了SOTA性能。
       STAR只用过去的轨迹进行预测，这可能无法发现不可预测的急转弯。额外的信息，如环境配置，可以被纳入框架以解决这个问题。
       STAR框架和TGConv并不限于轨迹预测。它们可以应用于任何图形学习任务。我们把它留给未来的研究。