状态反馈控制与状态观测器设置以及利用LQR方法求取状态反馈矩阵

状态反馈控制与状态观测器设置以及利用LQR方法求取状态反馈矩阵

文章是对现代控制理论控制器设计以及状态观测器设计部分的总结，面向对象是有一定基础现代控制基础的读者，偏重现在控制理论在配合matlab的应用，其中涉及到一些推导过程是为了给自己做笔记用的。

基于状态反馈的极点配置

对于开环系统有：$\dot{x}=Ax$
对于闭环系统有：$\dot{x}=Ax+Bu$ ； 其中 $u=-Kx$
因为系统的输入，状态变化都跟系统的状态有关了，因此，系统的闭环的。
然后有$\dot{x}=(A-BK)x=A_{c}x$.根据$\left|\begin{array}{c}A-BK\end{array}\right|$根据不同的$k$向量可以得到不同的特征值$\lambda$，即系统的特征根，选择合适的$K$矩阵达到任意配置极点的目的（系统完全能控，输入u不受限）。选择不同的$\lambda$，改变Ac的特征值，就相当于改变系统的变化路径。根据需求设置不同的$\lambda$可以求得对应的反馈矩阵$K$.
使用matlab函数 $K=acker(A,B,J)$ 可以非常方便地求得状态反馈矩阵，其中$J$是系统极点地期望值向量。

LQR控制器

较短的调节速度和较少的能耗是互相矛盾，LQR控制器是在控制指标已知，控制系统的反馈参数可以使用LQR方法求得，下面举例说明：

设有状态方程：
$$\left[\begin{array}{c}\dot{x_1}\\ \dot{x_2}\end{array}\right]=\left[\begin{array}{cc}0& 1\\ \frac{g}{l}& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{c}0\\ -1\end{array}\right]u$$
令
$$\left[\begin{array}{c}\dot{x_1}\\ \dot{x_2}\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$
得到
$$\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$
也就是最后系统最后会平衡在(0,0)点。

引入目标函数
$$J(z)={\int }_0^t(x^{T}Qx+u^{T}Ru)dt.$$
积分的前一项说明了对控制变量的变化的要求，后一项说明的是在满足要求的同时，又能使控制的输出最小。
其中Q为如下，且a，b，c均为正值。
$$\left[\begin{array}{cc}a& \\ & b\end{array}\right]$$

其中a，b，R的值都是根据需求设定的，如果我们希望在较少的时间内达到控制目的，可以令Q = [100,0;0,1]，R = 0.1，可以使用matlab算出K =[-43.1662 -9.8149]；如果我们希望消耗较少的能量达到控制目的，则可以设Q = [1,0;0,1]，R = 10，算出K=[-20.0050 -6.3332]，将参数带入仿真模型中可以得到下面的结果。

不难理解的是，较短的调节速度和较少的能耗是两个互相矛盾的要素，他们之间只能作一个调和仿真中也真反映了这种观点。值得注意的是，只有完全能控的系统才能作上面的操作，并不是所有系统都可以这么做，系统完全能控的判别条件即$Rank(Q_c)=n$，其中$$Q_c=\left[\begin{array}{cccc}b& AB& ...& A^{n-1}B\end{array}\right]$$

系统稳定点设置

如果希望把稳态点定在$$x_{1exp}=0.1$$的地方，可以令
$$e=x_{1exp}-x_1$$
有
$$\dot{e}=-\dot{x_1}=-x_2$$
从而我们得到新的状态方程（系统只能用状态方程表示，而状态反馈控制作为唯一地手段只能使得方程中的状态的变化为零，设计控制器使得$x_1\to x_{1exp}$首先要满足$e$的终止为0）
$$\left[\begin{array}{c}\dot{e}\\ \dot{x_2}\end{array}\right]=\left[\begin{array}{cc}0& -1\\ -\frac{g}{l}& 0\end{array}\right]\left[\begin{array}{c}e\\ x_2\end{array}\right]+\left[\begin{array}{c}0\\ -1\end{array}\right]u+\left[\begin{array}{c}0\\ \frac{g}{l}{x}_{1exp}\end{array}\right]$$
但是我们发现这个状态方程的稳定值是
$$\left[\begin{array}{c}{e}_f\\ x_{2f}\end{array}\right]=\left[\begin{array}{c}\frac{g}{l}{x}_{1exp}\\ 0\end{array}\right]$$
与预期的目标值不一致，于是，我们可以把控制器分为两个部分：
1、稳定系统的部分；
2、调节平衡点的部分。
令$$u=u_1+u_2$$
其中
$$\{\begin{array}{l}{u}_1=\left[\begin{array}{cc}{k}_1& k_2\end{array}\right]\left[\begin{array}{c}e\\ x_2\end{array}\right]\\ u_2=-\frac{g}{l}{x}_{1exp}\end{array}$$
代入方程得到
$$\left[\begin{array}{c}\dot{e}\\ \dot{x_2}\end{array}\right]=\left[\begin{array}{cc}0& -1\\ -\frac{g}{l}+k_1& k_2\end{array}\right]\left[\begin{array}{c}e\\ x_2\end{array}\right]$$
然后我们设${\lambda }_1={\lambda }_2=-1$得到 $k_1=1+g/l，k_2=-2$.
实际上，得到上面的式子以后，我们也可以按照LQR的控制器的设计方法，设计一个合适的状态反馈$u_1$，最后求得$u$作为最终的反馈式。

状态不可测

我们曾经假设u = - λx，此时便默认x是可测的，当x未知的时候，我们就不可能对系统作状态反馈，此时可以设计一个状态观测器，根据系统输出来估计状态。所谓状态观测器，其实就是根据系统的输入和输出来估计系统的状态。

状态观测器

设 $\hat{x}$ 为 $x$ (状态)的估计值，$\hat{y}$ 为 $y$ (输出)的估计值
系统的状态方程和输出方程为
$$\{\begin{array}{l}\dot{\hat{x}}=A\hat{x}+Bu+G(y-\hat{y})\\ \hat{y}=C\hat{x}+Du\end{array}$$

综合系统的状态方程和输出方程，有状态观测器($\dot{\hat{x}}$关于$\hat{x}$的表达式)：
$$\dot{\hat{x}}=(A-GC)\hat{x}+(B-GD)u+Gy$$

观测值必须满足收敛于实际值，综合状态观测器和状态方程可以得出：
$${\dot{e}}_x=\dot{x}-\dot{\hat{x}}=(A-GC)(x-\hat{x})=(A-GC)e_x$$

也就是估计误差$\dot{e_x}\to 0$，只需$(A-GC)$的特征值的实部等于0，只需找到一个G使得$(A-GC)$的特征值的实部等于0，这里特征值需要人为设定(系统能观就一定能找到)。
如果系统可观，则$Rank(Q_o)=n$，其中$Q_o$为：
$$Q_o=\left[\begin{array}{c}C\\ CA\\ ...\\ C{A}^{n-1}\end{array}\right]$$

比如：有状态方程和输出方程：
$$\dot{x}=\left[\begin{array}{cc}0& 1\\ 2& -1\end{array}\right]x+\left[\begin{array}{c}0\\ 1\end{array}\right]u$$
$$y=\left[\begin{array}{cc}-1& 1\end{array}\right]x$$

其中$$Q_o=\left[\begin{array}{cc}-1& 1\\ 2& -2\end{array}\right]$$

即$Rank(Q_o)=1\ne 2$，则系统不完全可观。

状态观测器的应用

例如，在经典的弹簧阻尼系统中设$x_1=x,x_2=v$, 弹簧的劲度系数为$k$，阻尼系数为$b$，物块质量为$m$，则可建立状态方程
$$\dot{x}=\left[\begin{array}{cc}0& 1\\ -\frac{k}{m}& -\frac{b}{m}\end{array}\right]x+\left[\begin{array}{c}0\\ \frac{1}{m}\end{array}\right]u$$
$$y=\left[\begin{array}{cc}1& 0\end{array}\right]x$$

令m = 1, b = 0.5, k = 1，得到：
$$\dot{x}=\left[\begin{array}{cc}0& 1\\ -1& -0.5\end{array}\right]x+\left[\begin{array}{c}0\\ 1\end{array}\right]u$$
$$y=\left[\begin{array}{cc}1& 0\end{array}\right]x$$
求得$Rank(Q_o)=2$
设观测器的极点${\lambda }_0={\lambda }_1$，有
$$\{\begin{array}{l}{g}_1+0.5=-2{\lambda }_0\\ 0.5g_1-g_2-1={\lambda }_0^2\end{array}$$
令${\lambda }_0={\lambda }_1=-1$

解得$g={\left[\begin{array}{cc}1.5& -0.75\end{array}\right]}^T$ 通过改变

也可以使用matlab函数$G=acker(A^{\prime },C^{\prime },V{)}^{\prime }$直接算得反馈矩阵G，其中V为特征根组成的向量。

根据：$$\dot{\hat{x}}=(A-GC)\hat{x}+(B-GD)u+Gy$$${\lambda }_0,{\lambda }_1$的值，可以改变状态观测器的收敛速率。

综合以上结果，可以得到$$\dot{\hat{x}}=\left[\begin{array}{cc}-1.5& 1\\ -0.25& -0.5\end{array}\right]x+\left[\begin{array}{c}0\\ 1\end{array}\right]u+\left[\begin{array}{c}1.5\\ -0.75\end{array}\right]y$$
建立仿真模型，仿真10s。

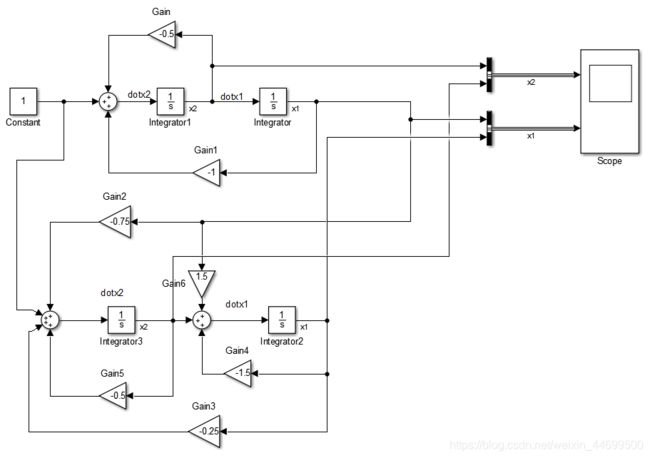
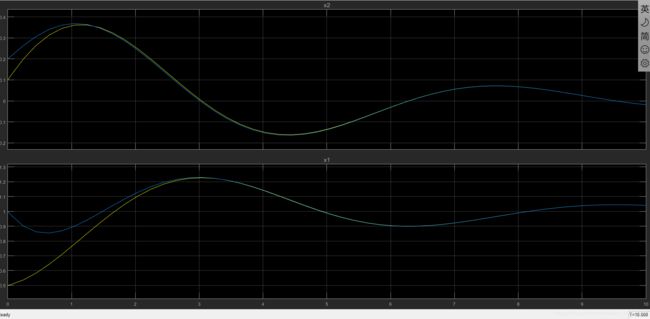
建立matlab仿真，并给状态观测器一个初始的估计误差，可以看到，状态观测器最终会收敛于真实值。

控制器与观测器分离原理

设系统是完全能控完全能观的，系统的状态是不能测量的。
首先，我们要实际观测器：
$$\{\begin{array}{l}\dot{\hat{x}}=A\hat{x}+Bu+G(y-\hat{y})\\ \dot{e}=(A-GC)e_x\end{array}$$
其中1式是状态观测器的表达式，其中含有u，y是为了利用输入输出估计状态；2式是状态观测器必须满足的条件，其中出现$\dot{e}$是为了利用特征矩阵收敛使得误差趋于0。亦即1式是实际要用的，2式是充分条件，根据他可以求得G矩阵。

然后设计控制器：
$$\{\begin{array}{l}u=-K\hat{x}\\ \dot{x}=Ax-BKu\end{array}$$

其中1式是反馈控制器的表达式，所谓控制器，亦即根据状态反馈确定输入，对系统实现控制，是我们要求的；2式是状态观测器必须满足的条件，是系统收敛的充分条件，根据它可以求得k矩阵。

为了求得G，K作以下证明：
根据定义：$\hat{x}=x-e_x$所以有$\dot{x}=(A-BK)x+BKe$
联立：
$$\{\begin{array}{l}\dot{e}=(A-GC)e_x\\ \dot{x}=(A-BK)x+BKe\end{array}$$

得：
$$\left[\begin{array}{c}\dot{e}\\ \dot{x}\end{array}\right]=\left[\begin{array}{cc}(A-GC)& 0\\ BK& (A-BK)\end{array}\right]\left[\begin{array}{c}e\\ x\end{array}\right]$$

即，只需$\left[\begin{array}{cc}(A-GC)& 0\\ BK& (A-BK)\end{array}\right]$特征值实部都为负即可。求其特征值：
$$\left|\lambda I-\left[\begin{array}{cc}(A-GC)& 0\\ BK& (A-BK)\end{array}\right]\right|=\left|\left[\begin{array}{cc}\lambda I-(A-GC)& 0\\ BK& \lambda I-(A-BK)\end{array}\right]\right|=\left|(\lambda I-(A-GC))(\lambda I-(A-BK))\right|$$
到此便实现了观测器与控制器分离计算。这里需要注意的是状态观测器的收敛速度必须高于控制器的收敛速度。因为我们需要一个准确的估计值才能完成好的控制。

控制器与观测器合并应用

还是上面的弹簧阻尼系统，设计状态反馈和状态观测器。设控制器的极点为（-2，-2），观测器的极点为（-6，-6），使用matlab函数算得$K=\left[\begin{array}{cc}3.0000& 3.5000\end{array}\right]$，$G=\left[\begin{array}{cc}11.5& 29.25\end{array}\right]$，建立仿真模型，仿真4s：

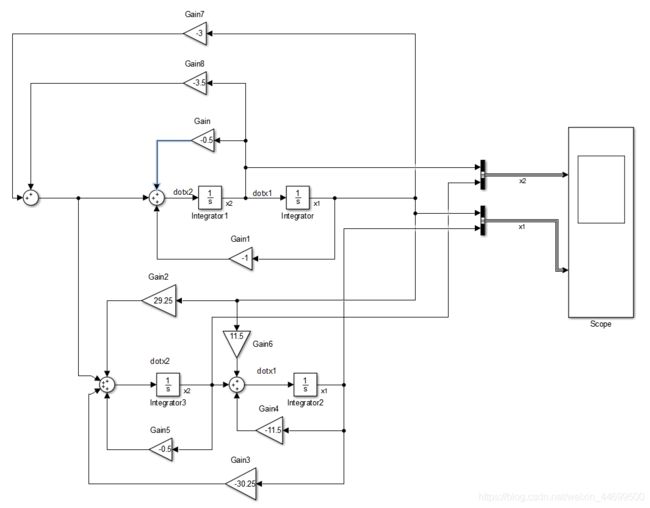
其中，黄线是实际值，蓝线是估计值，可以看到，系统得稳定速度大大加快。

值得注意的是，如果想在系统稳定前获得较稳准确的观测值，观器的收敛速度并不宜过快，虽然观测的收敛速度满足比控制器的收敛速度快后并不影响控制器对状态的控制，但是，状态的器过快的收敛速度会使得观测值有一个很大的超调，下面对比控制器相同时，不同观测器对系统的影响。

（左边[-6,-6],右边[-4.5,-4.5]）