《逻辑综合(logic synthesis)入门指南》

Hello, 欢迎来到逻辑综合的世界，在这里我将用尽可能通俗的语言，介绍什么是逻辑综合。

技术是不断进步的，因此本文会不断更，持续更新，记得收藏哦~~

目录

逻辑综合概述

技术概述

一、翻译

二、高阶优化

2.1 常数传递和冗余消除

2.2 算术运算优化

2.3 公共子表达式消除

2.4 资源共享

2.5 状态编码和状态机优化

三、逻辑表达方法

3.1 真值表

3.2 卡诺图

3.3 二级逻辑表达

3.4 BDD(Binary Decision Diagram)

3.5 多级逻辑表达

四、逻辑优化方法

4.1 代数法

4.2 布尔法

4.3 RM(Reed-Muller)极性变换

4.4 精确综合

4.4 小结

五、工艺映射

5.1 FPGA工艺映射

5.2 ASIC工艺映射

六、逻辑等价性验证

6.1 组合逻辑电路

6.1.1 概念

6.1.2 应用场景

6.2 时序逻辑电路

6.3 C2RTL

七、时序优化

7.1 时序约束

7.2 时序分析

7.3 时序优化

八、物理逻辑综合

总结

---

逻辑综合概述

逻辑综合(logic synthesis)是将用户所设计数字电路的高抽象级描述，经过布尔函数化简、优化后，转换到逻辑门级别的电路连线网表的过程。

设计的数字电路行为级模型通常用硬件描述语言（Hardware Description Language，HDL）描述，典型的HDL包括VHDL、Verilog、SystemVerilog，HDL主要在寄存传输级（Register Transfer Level，RTL）对电路进行高级抽象，避免一开始陷入低级别逻辑门、复杂连线等带来的设计复杂性。

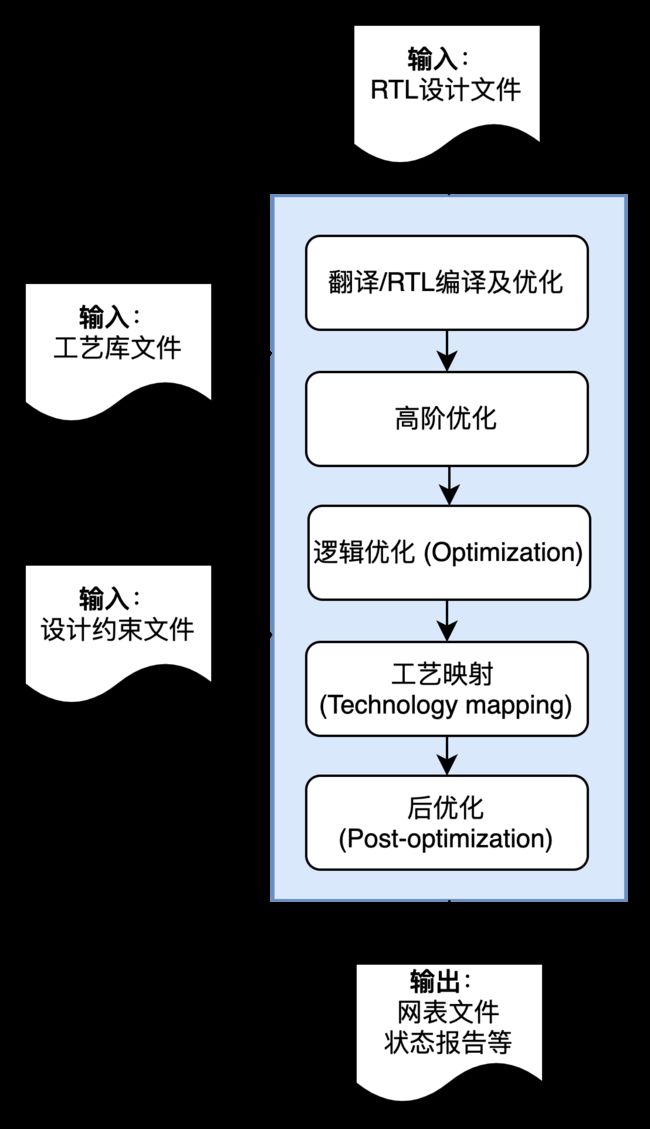
从RTL到工艺库网表的过程一般需要经历翻译、RTL优化、逻辑优化、工艺映射和后优化（post optimization）等阶段。因综合出的网表直接影响到后续的物理设计，自动化的综合技术是集成电路设计自动化（EDA）不可缺少的重要部分。

然而，从电路的高级抽象描述到实际连线网表，并不是一项简单的工作。在以前，这需要设计人员完成逻辑函数的建立、简化、绘制逻辑门网表等诸多步骤。随着电路的集成规模越来越大，人工进行逻辑综合变成了一项十分繁琐的任务。因此，自动化的综合技术是集成电路设计自动化(EDA)不可缺少的重要部分。

商用ASIC(专用集成电路)逻辑综合工具占有率最高的是Synopsys公司的Design Compiler (DC)，逻辑综合工具也是Synopsys公司1986年成立时的主营业务，其依靠出色的逻辑综合工具占据了较大市场份额并一举成为全球市值第一的EDA公司。IBM和UC Berkeley等单位联合开发的MIS(Multilevel Interactive Synthesis)综合系统是很多商用综合工具之母，我国在90年代初研发的熊猫系统在“巴统禁运”背景下填补了国内EDA空白，但是随着Synopsys公司1995年进入中国市场，国产逻辑综合工具乃至熊猫系统的发展陷入停滞。市场上所有的数字芯片设计均离不开逻辑综合工具，逻辑综合推动芯片设计效率大幅提升，同时进一步提升芯片设计的抽象程度，推动芯片设计从门级进入架构级和系统级。逻辑综合和布局布线也被分别认为是EDA设计流程前端和后端的“根技术”。

随着集成电路的规模的不断增大，逻辑综合工具的重要性日益凸显。首先，由于电路十分复杂，过去适合小规模、中规模集成电路的技术方法不再具有效率的优势，此外，在深亚微米级的超大规模集成电路中，元件的互连延迟变得十分复杂，但是这一情况对于电路的正常工作十分重要，现代的硬件描述语言和逻辑综合、物理设计工具可以很好地处理这些问题。将先进的硬件描述语言、逻辑仿真、逻辑综合等工具配合使用，可以提高设计工作的效率和准确程度。大约90nm工艺时，逻辑综合必须考虑后端，这不仅适用于时序问题，还需要诸如缓冲器插入，单元尺寸调整和功耗降低技术以及布局和设计无法完全分离的许多其他领域，这被称为物理级综合(physical synthesis)。

综合流程

给定高阶语言，如C、C++、SystemC等，描述的电路，工具能够将其自动编译成RTL级描述的电路，并将此作为门级逻辑综合的输入，这一过程被称为高阶综合。高阶综合的出现进一步提高了对数字电路的抽象处理，在行为级进行综合提高了设计人员的开发效率，早在2004年就出现了商用的解决方案，对复杂的专用集成电路（ASIC）和FPGA设计尤其有效。综合流程示意图如上所示。

与ASIC综合相比，FPGA综合工具因不同厂商生产的FPGA产品架构不同，厂商一般都有自己提供的工具，如Xilinx Vivado (之前为ISE)、Altrea Quartus II、国内紫光同创的Pango Design Suite (PDS)等，以及Synopsys公司提供的第三方工具Synplify (之前属于Synplicity公司)。FPGA物理设计则一般采用的是厂商自带的映射、布局布线工具。可以看出，一款高性能的FPGA不仅需要先进工艺下的架构设计，同时不能缺少针对FPGA产品特性的工具链。

技术概述

逻辑综合工具的输入主要包括：RTL文件或文件列表、标准逻辑单元库（Liberty)、SDC（Standard Design Constraints）约束文件、用户IP/Macro库文件、物理库信息、版图（DEF）文件、以及对综合流程的控制和配置脚本文件，如TCL命令等。其中SDC约束是设计中的一个重要文件，对电路的PPA进行约束，主要用来描述芯片的工作速度、边界约束、设计违例规则、特殊路径等，注意设计的不同阶段所采用SDC约束不同。比如说，综合刚开始时针对非精确模型，可以将时钟频率设置的高一些。SDC在时钟树综合和签核阶段都会用到，不仅仅是综合阶段专有。

逻辑综合工具的输出主要包括：状态报告用于报告工艺映射结果，特别是时序信息；导出工艺网表或者其他结果用于后续流程。

通用网表，又称为GTECH（generic technology）网表，与工艺网表相比较，GTECH网表没有具体的工艺信息，指的是其使用的逻辑门单元是一个符号，包含通用逻辑门（例如与或非，触发器等等）和通用运算符（加减乘除、移位、比较、选择等等），GTECH网表中仅包含逻辑功能，但可以对功耗、时延和面积（Power、Performance、Area，PPA）建模。以16选1多路选择器（multiplexer，MUX)为例，GTECH网表将其表示成16输入、4个输入选择、1个输出的16x1MUX；相比工艺网表依据工艺库信息可能将其表示成多个4x1MUX的级联形式。

逻辑综合工具主要包括五个阶段：翻译（translation）、高阶RTL优化、逻辑优化（logic optimization）、工艺映射（technology mapping）和后优化，每个阶段的基本任务说明如下：

逻辑综合基本流程图

1. 翻译：RTL编译及优化是将HDL转换成通用网表，同时在编译过程中进行优化；
2. 高阶RTL优化：高阶优化是对通用网表的典型电路和运算符进行优化和实现；
3. 逻辑优化：逻辑优化是对通用网表基于布尔代数进行化简，主要优化通用网表的节点个数、逻辑层级、开关活动性等；
4. 工艺映射：将优化后的电路映射到制造商提供的包含具体工艺信息（面积、时延、功耗、负载等）的库上，输出工艺相关的门级网表。其中ASIC工艺映射主要是标准单元库、FPGA工艺映射是查找表；
5. 后优化：后优化指的是工艺映射后的网表进行重新映射，运算符重新实现，buffer插入和器件尺寸选择等优化。为达到最好的PPA，通常需要引入时序约束，逻辑综合工具会根据时序要求，优化关键路径，在延时、面积和功耗中达到最佳平衡。

随着工艺的发展，逻辑综合优化的结果往往不能和后端布局布线的期望一致。因此，基于物理信息的综合技术被引入工具中，即综合过程中充分考虑物理信息，从而使逻辑综合和布局布线的优化具有一致性。

数字电路分为组合逻辑电路和时序逻辑电路，因此逻辑综合工具的主要研究对象是datapath和布尔逻辑函数等，涉及到有限状态机、时序/组合逻辑电路的表示方法，特别是适用于计算机处理的数据结构。以前，逻辑优化和工艺映射是分开的，逻辑优化又被称为“工艺无关的优化”（technology-independent optimization）。随着工艺的持续演进，已经从逻辑优化与工艺相分离的综合，演变到逻辑优化与工艺和应用场景融合的综合。

---

一、翻译

翻译是将RTL文件转换为GTECH（generic technology）网表，翻译的实质是一个HDL编译器，包括词法分析、语法分析和语义分析、中间表示优化、网表生成、网表优化等步骤。

• 词法分析：从左到右逐行扫描HDL源文件，识别分解出词法单元标记（token）关键词（例如module、assign等），标识符（例如fir_filter、clock_1p5等)，常量（例如12、4‘b1010等），逻辑操作/运算符（例如+、*、<<、&&等）
• 语法分析和语义分析：分析token序列形成满足语法结构的中间表示，比如module，变量，类型（wire还是reg，位宽表示），always块，敏感列表，赋值语句，循环语句，常数表达式，逻辑表达式，算术表达式等。语义分析是进行一些检查，比如变量的类型是否正确，位宽是否匹配，下标是否越界，敏感列表是否包含应有的信息之类的检查
• 中间表示优化：针对中间表示的优化，常见的有常数优化，运算优化，循环优化等。比如若有表达式的值在循环中不会改变，就可以把它放到循环外面，这样表达式只需要计算一次，即只生成一份逻辑电路，而不是通过循环生成多份，从而达到大幅优化的目的
• 网表生成：转换中间表示形成通用网表，比如逻辑表达式转换成逻辑操作电路，运算表达式转换成算术运算单元，边沿触发的always块里可以生成寄存器，case语句的变量赋值转换成多路选择器（MUX）等
• 网表优化：模块中各个always块和assign赋值分别生成网表后，这些网表形成整个模块的通用网表；同时也带来一些优化的机会，像常数，冗余提供了进一步优化的机会

常用的硬件描述语言有Verilog、SystemVerilog、VHDL等，这些描述语言提供了的基本结构，比如与或非门、寄存器、时钟等，也提供了抽象电路的描述，例如加减乘除、比较、移位等运算，还包括了较为高级的程序控制，例如if-then-else、for循环等。举一个Verilog的例子：

module dut (clk, in, out1);
  input clk;
  input in;
  output out1;
  reg[3:0] r;
  integer i;
  always @(posedge clk) begin
    r[0] <= in;
    for(i = 1; i <= 3; i = i + 1)
       r[i] <= r[i-1]
  end
  assign out1 = r[3];
endmodule

级联寄存器电路

编译器解析Verilog的输入，生成语法树和中间表示。中间表示需要包含module，语句，表达式，变量，常数等。中间表示可以被优化或者变换，例如上例中的循环语句可以被展开；循环变量i分别被不同常数例化从而得到

r[1] <= r[0];
r[2] <= r[1];
r[3] <= r[2];

下一步编译器将中间表示转换成网表，上面的三个非阻塞赋值语句转换成上图中右边三个寄存器，r[0]<=in1则被转换成最左边的寄存器。同时编译器将各个寄存器之前以及端口进行联接，形成一个不含工艺信息的通用网表。这个网表在转换生成过程中并不一定是最优的，可能存在一些冗余逻辑，编译器会将它们消除。

通用网表包含网表的基本逻辑信息，分模块来组织。每个模块有相应的输入和输出，包含基本逻辑单元（如与/或/非/异或、多路选择器、触发器、锁存器等）和操作符（如加减乘除、比较、移位、编码、解码等），通过连线联接而成。各个工具的通用网表的格式通常是不一样的，也不互相兼容。

---

二、高阶优化

高阶优化主要是基于通用网表的优化，涉及到以下内容：

• 常数传递并优化。
• 冗余逻辑消除。
• 算术运算降维，比如乘法变成移位，或乘法变成加法。
• 算术运算聚类，比如加法树的提取与平衡，加乘聚类。
• 公共子表达式消除，比如输入完全相同的同类型电路模块合并为一个模块。
• 位宽优化，比如缩小总线的位宽，删除无意义的多余位宽。
• 资源共享，将对运算结果的选择转换成操作数的选择，使得运算符被共享，从而减少面积。
• 状态机优化，比如状态最小化，可以减少用户写的状态机里的状态数目。
• 状态重编码，使用最优的编码方式给状态机重编码以达到优化面积和时序的目的等等。

2.1 常数传递和冗余消除

常数在用户的设计中很常见，能够利用常数的特点，尽可能地简化电路无疑是对网表优化是有帮助的。

虽然在HDL编译阶段也有常数优化，但是那个阶段主要针对模块内部。常数可以出现在模块例化的端口，需要在综合阶段优化。

以逻辑与门为例，根据下面的真值表：

a	b	a&b
0	0	0
0	1	0
1	0	0
1	1	1

如果输入a和b都是常数，结果也是常数，因此这个与门是可以优化掉的。下图所示输入都是0的情况为例：

与门常数传递示例(两个输入皆为0)

如果输入只有一个是常数，也可以进行优化下图中左图的电路由于其中一个输入为0，逻辑与的结果为0，因此可以优化成右边的电路，0直接连接到与门之后的电路，同时该与门以及与门的另一个输入的电路成为冗余，可以优化掉。

与门常数传递示例(一个输入为0)

类似的有关逻辑门的优化还有：

优化产生的常数可以对后面的电路继续提供优化的可能。因此常数优化是一个传递的过程，同时也会不断地产生冗余逻辑。另外，在逻辑优化的过程中也可以产生或发现逻辑电路中的常量（例如通过更复杂的逻辑分析可能确定一部分逻辑为永真或永假），所以通常在逻辑综合过程中进行多次的常数传递和冗余优化。

2.2 算术运算优化

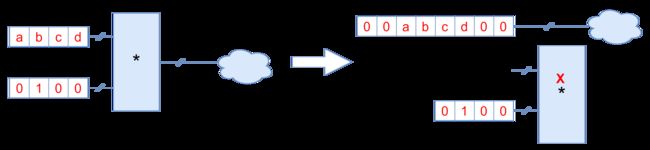
RTL编译后，通用网表中也保留算术运算单元。依据算术运算的规则，综合过程中也会对算术运算单元进行优化。

跟逻辑门的常数优化相似，当运算单元的输入是常数或者部分常数时，可以将运算单元优化或者缩小位宽。运算单元的位宽越大，电路就越复杂，需要更大的延时和面积。缩小位宽能起到优化电路的作用。下图分别表示优化过程中消除或者缩小算术运算。

算术运算消除示例

算术运算位宽缩小示例

在满足一定的条件下，算术运算可以降阶化简。例如，乘以2的N次方的运算可以降阶成左移N位。在数字电路中，常数移位并不占任何资源。因此，下图所示的转换可以优化电路。

算术运算降阶示例

2.3 公共子表达式消除

在RTL设计中，经常会出现重复计算的表达式，可能是逻辑操作，也可能是算术运算，本小节主要阐述的算术表达式的共享。如下图所示，A+B出现在通用网表电路中多次（即+运算重复多次），通过共享表达式A+B，只用一个+运算，从而达到优化电路的目的。

公共子表达式消除示例

由于一些算术运算如加乘满足交换律和结合律，所以A+B和B+A可以认为是同一个表达式。而且针对A+B+C和A+D+B，提取公共子表达式A+B能够节省一个加法运算单元。

2.4 资源共享

资源共享主要是针对数据通路中费耗资源较多的单元（比如算术运算），通过选择、服用的方式共享，达到减少资源使用和优化面积的目的。下图中左边的电路表示的是：

X = E ? (A * B) : (C * D);

需要用到两个乘法单元和一个选择器；转换成右边的电路，表示的是：

X = (E ? A : C) * (E ? B : D);

需要用到一个乘法单元和两个选择器。因为选择器所需的资源比乘法小，所以右边的电路比左边电路面积简化。

资源共享示例

2.5 状态编码和状态机优化

状态机优化是一种对电路进行高层次优化的方式，其解决的主要问题是：如何找到一个更加合理的等价状态机模型，从而用更少的成本，更优秀的性能来实现符合预期功能的电路。状态机优化的最主要内容包括状态最小化和状态重编码，前者倾向于在状态机整体结构上进行优化，后者倾向于在具体电路实现逻辑上进行优化。

状态最小化，也就是找到或者构建一个状态数更少的，转移关系更少的，和原状态机等价的有限状态机，作为新的电路模型，实现简化电路结构的目的。状态最小化的三种主要方式有：

• 去除不可到达状态。状态机内可能存在任何情况下，都无法通过状态转移情况到达的状态，这些状态时状态机的无效冗余状态
• 合并等价状态，将完全等价的状态进行合并
• 使用最大兼容组的原状态机内的状态进行覆盖。通过状态机内部状态之间的兼容关系，将状态按照一定的规律进行分组，在符合一定约束条件的前提下，对原状态机内的状态进行覆盖，实现状态最小化

编码风格会对状态机编码结果产生相应的影响，如顺序数二进制编码可以减少触发器数量，但实现电路使用的逻辑单元数量更多；独热码编码的效果相反；格雷码编码是一种减少功耗的编码方式，但实际情况很难实现。状态机编码风格需要根据设计需求做出选择。

状态机的编码方式是状态重编码的主要研究对象，它决定了电路功能实现的具体逻辑。编码方式决定了电路中每个触发器单元和输出的每一位对应的真值表。可以将状态机的编码方式作为评估电路实现成本和性能的指标，或者作为预测综合之后的指标（逻辑综合可能会对真值表产生影响）。通过设计成本和性能预测的公式，来评估状态重编码的结果，并通过一定的启发式算法来快速收敛，求取最优解。

---

三、逻辑表达方法

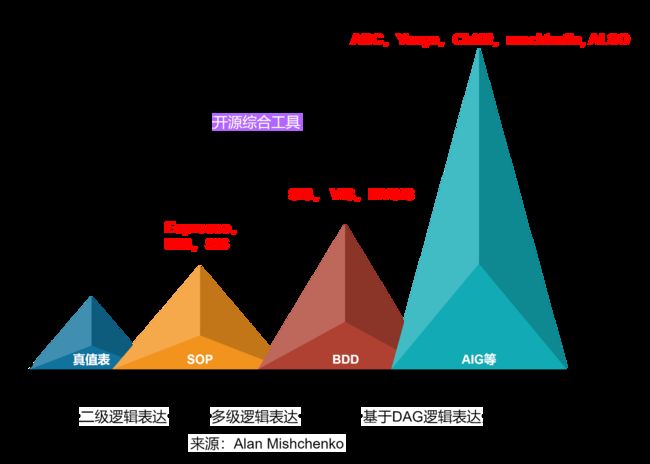
布尔优化的发展历史，从二级逻辑优化、多级逻辑优化到基于DAG的逻辑优化，经历了三个大的发展步骤，主要驱动因素是解决综合问题的规模越来越大，以及所对应的电路实现形式发送变化。因此对逻辑表达方法的研究也经历了几个不同的时期。

逻辑优化方法与逻辑函数的表达方法密切相关。在集成电路发展的早期，因可编程逻辑阵列（Programmable Logic Array，PLA）的兴起，积之和（Sum-of-Products，SOPs）被用来表示布尔逻辑函数，经优化后的函数可直接用PLA实现。而随着函数规模的增大，以SOP为代表的逻辑表达式因其仅能表示二级（Two-level）函数，在表达较大规模函数时复杂度剧增，有着明显的局限性。相比于二级表达，多级（Multi-level）图形化的布尔逻辑函数表示方法成为主流，例如二元决策图（Binary Decision Diagram，BDD）、与非图（And-Inverter Graph，AIG）等，据此基于布尔代数发展了较多逻辑优化方法，如下图所示。以下按照逻辑函数的表达规模分别进行介绍。以下部分内容来源于文献：储著飞, 王伦耀, 夏银水 "基于多逻辑域的逻辑综合研究进展," 微纳电子与智能制造, 3(2):64-73.

逻辑表达方法的发展简史

3.1 真值表

给定逻辑函数所有可能的输入组合，真值表显性的列出函数值。给定函数，其有种输入组合，每个组合对应一个输出，，则真值表为。

三输入多数运算门（majority-of-three，MAJ），又称为表决器，有奇数个输入，当且仅当超过半数的输入取值为真（true）时，输出为真，否则输出假（false）。以三输入多数运算门（）为例，三个布尔变量、和的多数运算函数，记为或者，因此真值表长度为，即11101000，随着变量增多，真值表的规模呈指数级增长，因此也常用十六进制表示，0xe8，如下图所示。真值表是一种典范表达（Canonical Representation），因此如果两个函数的真值表相等，则认为这两个函数等价。

多数逻辑门真值表

3.2 卡诺图

真值表可表示成卡诺图，在一个包含n个变量的逻辑函数中，包括全部n个变量的乘积项，若每个变量都以它的原变量或者反变量的形式出现一次，则称该乘积项为最小项。

逻辑函数的卡诺图就是将函数的最小项表达式中的最小项填入到一个方格图中，可以方格图中直观的找出相邻的最小项并进行化简，如下图所示，四个变量共有16个最小项，卡诺图也有16个方格，方格中“-”常表示无关项（don't care），给函数化简带来更多机会。但卡诺图表示的变量有限，仅用于不超过6个变量的函数综合。

四变量卡诺图示例

3.3 二级逻辑表达

逻辑函数可以表示成析取范式（Disjunctive Normal Form，DNF）、合取范式（Conjunctive Normal Form，CNF），其中DNF又被称为“积之和”（SOP），CNF又被称为“和之积”（Product-of-Sum，POS）。

一个典型的例子就是根据真值表中最小项表示一个逻辑函数，以为例，从真值表所示的最小项可以得出的SOP形式

 

该公式可进一步化简得到更紧凑的表示。与SOP对偶的是RM形式，RM形式将所有的乘积项通过“异或”而不是“或”算符联结，又称为ESOP（Exclusive-or SOP）形式。

以上均为二级逻辑表达，从对应的逻辑网络中（下图）可以看出，依据二级逻辑表达得到的逻辑网络从输入到输出的逻辑级为2。

MAJ逻辑函数的逻辑图

3.4 BDD(Binary Decision Diagram)

BDD是一个有向无环图（Directed Acyclic Graph，DAG），每个中间节点执行香农分解中的一步。其中香农分解又称为香农展开，是对布尔变量的表示方式，可以将任意布尔函数表达为其中任何一个变量乘以一个子函数，加上这个变量的反变量乘以另一个子函数，如下面的公式所示。香农展开后的函数可用一个数据选择器来实现。

BDD规模的大小受到变量排序影响，且存在冗余、重复和同构节点，1986年提出的ROBDD（Reduced Ordered BDD）通过固定变量顺序并进行约简得到逻辑函数的典范表达，我们通常所称的基于BDD的逻辑综合大多指的是ROBDD。下图所示为两变量异或函数的BDD及其约简后的ROBDD图形表示，图中虚线代表布尔变量取“0”，而实线代表布尔变量取“1”。举例来说，图中当，时，函数的输出值为1。

异或逻辑函数的BDD图及约简后的ROBDD

3.5 多级逻辑表达

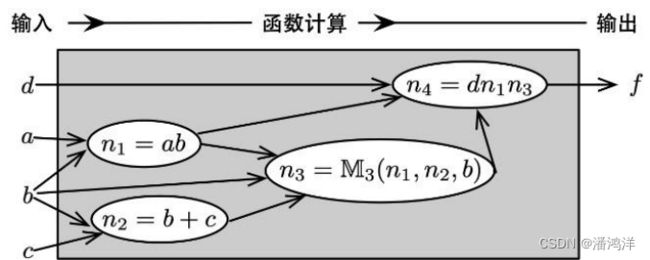
基于二级逻辑表达，不难推广到多级逻辑表达，二级逻辑表达因逻辑级仅为2，因此速度快，但面积较大。多级逻辑网络用于当代超大规模电路设计，二级逻辑仍在小规模电路或者子电路中发挥作用。

多级逻辑网络可看成是有向无环图，包含初始输入和输出（Primary Input/Output，PI/PO），内部节点，以及连接边。其中内部节点可定义逻辑函数计算规则，节点的连接边定义函数的输入和输出关系。早期用于综合的多级逻辑网络如下图所示。该例中PI集合，PO集合，内部节点集合，连接边集合。

多级逻辑网络示例

内部节点表示的函数类型和输入不受限制的前提下，所生成的逻辑网络就越紧凑，但是执行逻辑优化效率却不高，这主要是优化时需要考虑更多的约束条件，例如节点的类型和输入都要经过程序判定，此类网络又称之为异构逻辑网络（Heterogeneous Logic Network）。与之对应的是限定每个内部节点所允许执行的逻辑运算和输入的个数，以此构成同构逻辑网络（Homogeneous Logic Network）。

例如AIG中所有的内部节点仅执行两输入AND操作，连接边包含常规边（Regular Edge）和补边（Complemented Edge），其中后者代表需添加反相器。MIG亦可用于逻辑表示。下图所示为全加器的AIG和MIG逻辑网络，其中‘’表示两输入AND，实线/虚线分别代表常规边和补边。

全加器的AIG和MIG逻辑网络

---

四、逻辑优化方法

逻辑优化是针对现有的逻辑表达进行化简，在逻辑功能一致的前提下优化逻辑函数的逻辑深度、开关活动性、文字数（Literals）或者节点个数，它们分别对应电路的性能、功耗和面积，统称为PPA优化。

二级逻辑表达，即SOP优化，主要是用Quine–McCluskey算法得到精确解和用启发式方法得到近似最优解，后者处理问题的规模更大也最为常见,BDD优化也有很多学者针对性研究出精确算法和启发式算法.

本节主要介绍多级逻辑网络中用到的优化方法，在现实应用中也最为常见。总体分为代数法、布尔法、RM极性变换法和精确综合法。

4.1 代数法

代数法主要指的是基于多项式代数（Polynomial Algebra）发展而来的方法，将逻辑代数中变量看成普通代数变量，执行抽取、替代、分解、重写（Algebraic Rewriting）等优化步骤。以下通过举例简要介绍。

抽取：从多个表达式中抽取相同的因子。例如和的相同因子为，则抽取后的表达式如下式所示。

如何提取相同的因子是关键，因子可以是单项式或者多项式，该例子中用到了多项式因子。

替代：利用现有的表达式作为一个额外输入来替代被优化函数的输入。例如逻辑函数和，则尝试用作为的一个输入。该例中为的因子，可以达成该目标，即。注意替代中作为因子已经存在，而抽取则需要去搜寻因子。 

分解：将一个较大规模函数分解成两个较小规模函数。函数分解实现的形式有很多种，一种最直接的方法是通过代数分解，例如将一个函数写成形式，其中为因子，为商，为余数。例如，通过引入一个新变量，则，。分解可以以递归的形式持续进行，与替代不同的是，因子构成了一个新的变量。

重写：重写基于代数公理系统在逻辑网络中执行变换，这里的代数包含一般代数和布尔代数，由于历史原因，曾经被称为代数重写。在AIG中，考虑代数等式，通过下图所示构造相应的AIG不难发现，可通过灵活的变换优化AIG的节点个数或者信号的逻辑深度。

AIG重写示例

4.2 布尔法

代数法因将布尔变量看成一般变量，并没有充分用到布尔代数的空间表达能力，布尔法则弥补了这一缺点。布尔法主要用到函数的无关项集合（Don't Care set，DC set），以此为基础将一个函数转换为另外一个函数但是不影响函数的输出结果。

例如，，可推算变量的输入模式和不会发生，因为当时，和必定都为1。据此可将函数简化为。

因此布尔法优化需要计算节点的无关集(Don't care set)，在这方面一些开源工具里基于SOP、BDD等发展出一系列方法可供借鉴。

4.3 RM(Reed-Muller)极性变换

除了传统布尔逻辑，布尔函数也可用基于“与/异或（XOR）”的Reed-Muller（RM）逻辑实现，研究表明RM逻辑在对算术电路综合时展现出较好的性能，而且综合出的电路易于测试。在RM逻辑中，按照变量的极性可将RM综合分为固定极性（Fixed-Polarity RM，FPRM）和混合极性综合（Mixed-Polarity RM，MPRM）。固定极性指的是ESOP乘积项中，变量不能同时出现原变量和反变量（取非）；而混合极性则允许原变量和反变量同时出现。

例如函数，因没有变量同时以原变量和反变量形式出现，则该表达式是固定极性ESOP，因三个变量均是原变量，以二进制数来表示，即该ESOP的极性为。在其他极性下的展开式如下所示

而在混合极性下，可见RM逻辑表达式可根据极性展开优化表达式的文字个数，实现面积优化，或通过抑制冗余跳变实现功耗优化等。

4.4 精确综合

给定逻辑算符，如何用最少的节点或者逻辑深度来实现布尔逻辑函数一直是关注的热点问题，与前述的启发式综合方法相比，精确综合能输出逻辑函数的最优表达形式。特别是近年来随着算力的提升，精确综合受到广泛关注，详见我的另一篇博客《精确逻辑综合入门指导书》。

例如，给定十六进制真值表表示的逻辑函数0x1234，对应的二进制为0001 0010 0011 0100，输入变量分别为a，b，c，d，若限定可用的逻辑算符集合为和反相器，经精确综合得到的表达式如下式所示。

因此最少需要5个逻辑门实现该函数，注意得到的表达式不是唯一的，可能存在其他不同的表达式，但是最低需要5个逻辑门。目前研究的较多的是基于布尔可满足性（Satisfiability，SAT）的方法。

4.4 小结

在优化中常综合使用以上介绍的方法，以下简述每种方法的优缺点和用法：

• 代数法优点是运行速度快、优化结果适中、可为其他方法提供一个较好的初始解；缺点是得到的结果是次优解；可通过循环多次代数法优化直到解不能改进为止，或者辅以其他方法跳出局部最优再循环。
• 布尔法的优点是以全局视角得到高质量解，充分利用了布尔代数的本质；缺点是计算稍复杂，消耗更多时间；可协助代数法跳出局部最优。
• 精确综合法的优点是得到的是最优解，也可与工艺相关；缺点是运行时间长，搜索空间可能是无限的，不能在有限时间获得解；一般通过对小规模电路离线求解，构建最优逻辑表达数据库，然后基于该数据库进行在线综合。
• RM极性变换可用于算术电路或者加密电路等特殊电路的综合场景中，与上述三种方法配合使用。

---

五、工艺映射

工艺映射是将通用网表转换成指定工艺的标准单元网表。

经过高阶RTL优化、翻译和逻辑优化的网表还没有和具体的工艺相结合。工艺映射后得到的网表为工艺网表。逻辑电路中的时序逻辑（触发器flip-flop ，FF或寄存器latch）和组合逻辑分别映射。通常时序逻辑的优化和映射早于组合逻辑的优化和映射。

时序逻辑映射的重点在正确性。寄存器（包括FF和latch）的控制组合有很多，有同步或异步或都有，有清零或置一或都有，有上升沿或下降沿驱动，等等。时序逻辑映射需要在标准单元库中查找最佳的寄存器元件并且功能正确的映射到电路网表中。

组合逻辑映射是将已经优化好的组合电路转换成标准组合单元。以下重点介绍组合逻辑电路映射成FPGA和ASIC的技术点，两者的主要区别在于映射的对象不同，分别是查找表和标准单元。

5.1 FPGA工艺映射

FPGA基本结构

 FPGA基本结构如上图所示，基本逻辑单元包含一个查找表和触发器，以及数据选择器，可实现任意的时序和组合逻辑。这里介绍的主要是组合电路如何映射到查找表上。下图展示了一个多级逻辑网络映射到4输入查找表的过程。图中不同的颜色代表对逻辑子网络的一个覆盖，每个覆盖的输入小于等于4，输出为1，因此左边的逻辑网表被映射成右边的2个4-LUT构成的查找表网络。

逻辑网表到LUT网表映射示意图

 对于一个逻辑网表，一个K-LUT可实现任意K个输入以内和1个输出的组合逻辑函数，因此，网表中的节点可以忽略其逻辑功能差别，将逻辑门抽象成节点，门电路间的连线抽象成节点之间的有向弧，整体上逻辑网表就是一个DAG。因此，FPGA的工艺映射问题就是如何利用K输入的LUT去覆盖一个经逻辑综合后生成的门级网表，得到一个功能等价的K-LUT工艺网表。

FPGA工艺映射中如何得到一个好的cover是至关重要的步骤，下图所示步骤中主要包含割枚举（cut enumberation），依据不同的优化目标，例如面积或者时延等，对割进行挑选和覆盖，最终输出工艺网表。

 FPGA基于结构映射框图

 如下所示，割枚举指的是对逻辑网络中的每个点枚举出所有K-feasible的割，下图给出了顶点g的两种3-feasible的割，其中割一的叶子节点为{pef}，覆盖了g和q这两个点；而割二的叶子节点为{stq}，可以看出其覆盖了四个点。

顶点g的割示例一 顶点g的割示例二

 割排序（cut ranking）指的是对每个割根据不同的优化指标评估该割若被选定为覆盖时潜在的收益，常见的评估目标是面积和时延。通过拓扑排序进行遍历，从原始输入（Primary Input，PI）到原始输出（Primary Output，PO）。

割选择指的是对每个节点选择一个“最好”的割，同样以面积或者时延为选择目标，遍历顺序和割排序评估相反，从PO到PI。其中割排序和割选择可根据实际情况多次迭代改进。

以上步骤完成后，就会确定最终的一个覆盖，得到LUT网表。

5.2 ASIC工艺映射

和FPGA工艺映射不同的是，ASIC工艺映射所映射的对象是工艺库中的众多逻辑单元，而不是FPGA中的查找表。总体来说，从流程上看，ASIC映射需要基于工艺库构建由简单逻辑单元构成的复杂逻辑单元，在割枚举和覆盖过程中共同考虑逻辑功能匹配的简单单元和复杂单元，所选用的成本函数基于单元库中的延时和面积信息来加以评估。

ASIC的逻辑门，通常仅限于通过从门工艺库中进行选择来实现。门是特定实现工艺中可用的基本元素；工艺库是这些门的集合。假定工艺库由门的有限集合组成，这些库通常由数百个门和顺序元件组成，如锁存器和触发器，为特定技术手动设计了高度优化的布局。每个门都被分配了许多与不同成本函数相关的值，在这些值下它将被优化。例如，为每个门分配一个值，称为门的面积，表示门占用的物理面积，然后逻辑设计者被限制在他们的逻辑电路中使用这些门。

下图显示了一个简单的库的组合子集。显示了库单元名称、相关面积成本、它们的功能以及它们在两输入与（NAND2）门和反相器（INV）方面的表示。给定一个工艺库，ASIC工艺映射的问题是找到一个多级电路等价于给定的布尔网络，这样它由库中的门组成并且成本最低，可以是面积、延迟、可测试性或功耗得到的电路。

门的工艺库

工艺映射的系统方法基于图覆盖（Graph Covering）的概念。通过这个概念，工艺映射问题可以被看作是通过从库中所有门的模式图集合中进行选择来寻找主题图的最小成本覆盖的优化问题。此外，任何覆盖的限制是覆盖中一个模式的输入必须是覆盖中其他模式的输出。否则，这意味着一个模式的输入来自另一种模式的内部节点。由于这些内部信号值在图外部不可见，因此任何没有这种限制的覆盖都没有意义。

如图(a)中的覆盖是合法的，而图(b)中的覆盖是不合法的。在图覆盖中，要覆盖的布尔网络通常以特殊形式表示，它被称为主要图或主要DAG。除了要覆盖的布尔网络外，每个库门也以这种特殊形式表示。每个实现都称为模式图或模式DAG。ASIC工艺映射的优化问题现在可以表述为：通过模式DAG找到主要DAG的最小成本覆盖。

（a）合法覆盖（b）不合法覆盖

工艺映射的结构方法的主要缺点是它们依赖于初始电路结构（即结构选择）。如果结构不好，启发式和迭代恢复都不会改善映射结果。考虑到在工艺无关的优化过程中，我们可以自由更改网络结构，但无法准确估计对下游映射的影响，甚至在某些方面，初始或中间网络结构可能比最终网络结构更好。因此，选择最优的覆盖模式是图覆盖算法的一个重要考虑因素，此选择会影响覆盖问题的解决方案范围和所需模式的数量。

---

六、逻辑等价性验证

电路等价验证有两个场景——组合逻辑等价及时序逻辑等价，其最终目标是验证两个电路在相同输入条件下，输出都相等(时序—每一拍都相等)。

6.1 组合逻辑电路

6.1.1 概念

组合电路等价性检查是指在一个组合电路经过变换之后，穷尽地检查变换前后的功能的一致性来证明设计的变换没有产生功能上的变化。这里所说的设计变换可以是综合（Synthesis）、布局布线（Placement and Routing）、测试（Testing）、时钟树的插入（Clock Tree）、扫描链（Scan Chain）的重排、FPGA到ASIC的转换等等。

如果要对一个现有的门级或物理级网表写出其RTL模型，以使原来的设计能够重用，这时也可以利用等价性验证。

另外，如果设计者要将原来的设计的功能进行必要的修改，等价性检查产生的信息可以用来帮助设计者确认所做的修改是否达到了目的。

6.1.2 应用场景

目前组合电路等价验证主要应用在RTL级别与门级组合电路之间的等价验证、以及门级与门级电路之间的等价验证。

1、RTL与门级组合电路的等价验证

在当前主流等价验证方法中，RTL与门级组合逻辑的等价验证最终仍然会转换为门级与门级的等价验证。在RTL转换为门级组合电路的过程中，需要注意以下几点：

在RTL语句中，可能存在无关项（don’t care），此时进行逻辑综合时，生成的门级网表可能并不唯一，因此可能存在有多个门级组合电路与RTL电路逻辑等价，但是这些门级电路互相之间逻辑均不等价的情况。这种情况会大大增加组合逻辑等价验证的难度，因此在设计电路时，应该尽量避免使用无关项。

由于目前门级组合电路的验证、尤其是针对不同结构的算术门级电路的验证还存在理论上的困难，因此一些综合工具会将RTL中的算术语句综合时产生的门级电路结构特征进行记录生成辅助文件，在进行验证时验证工具根据此辅助文件的信息对RTL转换为门级电路时进行指导，从而大大提高验证的速度与准确率。而如果不使用此辅助文件直接对RTL与门级电路进行等价验证的话，则很可能在很长时间内都无法验证得到结果从而最终不得不放弃验证强制终止。

2、门级与门级组合电路之间的等价验证

当前常见的门级组合电路等价性检验大致可以分为两类：功能性的和结构性的验证方法。但这两者间没有绝对界限。功能性方法一般先构造两个电路的规范表示形式，如真值表、布尔表达式、或二叉决策图（Binary Decision Diagram），当且仅当它们的规范形式同构时，这两个电路功能等价。

需要特别强调地是：BDD最常用的规范形式是简化的有序二叉决策图（Reduced，Ordered BDD，ROBDD）。在规范表示后，就进行等价性检查，这通常需要把它们当成有限状态机，并构造这两者的积自动机。Brand等在1993年的论文中将这种计算模型称为Miter。它通过把两个状态机对应的每一对原始输入连接到一起，同时把相对应的每一对原始输出输入到一个异或门，而这些异或门构成了积自动机的输出。如果对于每一个输入序列，积自动机的每个原始输出恒为0，那么这两个电路就是等价的。换句话说，就是对于任何输入向量和可达状态，积自动机的原始输出响应总是为0。通常，证明状态机等价性的第一步是从初始状态开始，计算所有可达状态，这就是典型的基于有限状态机遍历算法。尽管最近二十多年里，由于BDD方法的研究进展使得基于有限状态机遍历算法有了很大进步，但面对实际的大型设计仍然可能会因构造BDD的表示导致内存爆炸。这是因为BDD算法的特点：它对电路原始输入变量的排序十分敏感。对于某些不存在好的变量排序的电路，BDD的大小可能随变量个数呈指数增长。

为了克服上述符号方法的不足，Brand等提出了利用电路结构相似性来分阶段完成组合电路验证的策略，这就是结构性的验证方法。它通过识别电路内部的等价结点，并利用这些等价结点的功能蕴涵来简化验证问题。内部等价结点常被称为断点（cutpoint），识别潜在断点的常用方法有随机模拟、ATPG方法、基于BDD的方法以及基于可满足性（SAT）的推理方法。所有潜在的断点找出后，依据一定的规则，将整个系统验证分解为关于这些断点子集的较小的验证任务，分别进行验证。

目前的组合电路等价性检验方法大多数都是按结构性检验的基本框架再结合功能性方法进行验证。首先提取两个被比较电路的内部相似性，推导出各断点之间的特殊关系，如等价性、蕴涵及可置换性等等。然后使用这些关系，把等价性检验过程分解为关于这些断点子集的较小的验证任务，分别完成。总的算法是从原始输入向原始输出方向遍历两个电路，从已知的断点演绎出新的断点，直到所有的相应原始输出被证明等价，或者找到某个输入向量使得两个电路输出不匹配。

结构性方法的提出使得等价性检验速度有了显著提高，而且可以成功地验证较大的设计。这引起了更多学者的兴趣，提出了许多推广或改进的方法。近20年来出现了不少将BDD与自动测试向量生成（Automatic Test Pattern Generation，ATPG）或布尔可满足性（SAT)，随机模拟等手段相结合的办法，还有部分学者提出使用功能学习或者递归学习来验证电路之间的功能等价性，实质上是使用学习的方法来识别电路内部的结构相似性。这其中布尔可满足性算法的研究取得了巨大的进展，各种优秀的SAT程序不断产生，不少人提出了利用SAT来进行等价性检验并取得了巨大成功。最终使等价性检查成为了IC设计验证中最广泛使用的形式验证方法。

6.2 时序逻辑电路

组合逻辑等价验证是指两个被验证电路的触发器可以一一配对情况下，针对每一对触发器驱动逻辑的等价验证。这样两个电路的等价就被分割为多个逻辑规模很小的电路等价问题。

时序逻辑等价验证是指两个电路的触发器无法一一配对情况下的只保证电路输出等价的验证。触发器无法配对通常是做时钟优化的retiming和做功耗优化的clock-gating造成的。其他原因还包括冗余逻辑和don't-care优化。

时序逻辑等价验证一般会结合组合逻辑验证进行。即假设可以配对的触发器等价并验证去驱动逻辑的等价性。剔除失败的配对重新验证直到剩余配对全部通过。这些等价触发器合并后再对电路输出做一般的形式验证，以证明两个电路的等价性。

6.3 C2RTL

C2RTL是对于C语言模型和RTL代码模型之间的一致性检查。

检查过程是：首先对RTL和C++设计模块进行形式化建模和分析这些模块的行为。

形式化建模包括建立输入和输出之间的transaction，这些transaction可以是多个时钟周期、无时钟组合逻辑的传输、C++ function功能。不过多周期的transaction必须有个周期上限。RTL功能仿真一般会把激励后的输出结果与参考模型对比找到问题，但是如果数据位宽过宽，会很难进行充分验证。比如两个16位宽的数据输入需要40亿个仿真激励才能实现全功能覆盖。而C2RTL工具比仿真更容易达到全功能覆盖，也能发现一些特殊案例。

C2RTL检查工具支持Verilog，VHDL和SystemVerilog的可综合子集，同时也支持C++的大部分语法。工具软件会把输入的设计转变成Data flow graph（DFG）并且进行建模。工具支持两个C++模型之间的比较，两个RTL设计之间的比较，C++参考模型和RTL设计之间的比较。

---

七、时序优化

基于时序的优化是逻辑综合的重要步骤，直接关系到芯片的性能，在优化指标中也需要通盘考虑功耗、延时和面积（Power Performance Area，PPA）。首先需要对设计进行时序约束，其次综合工具对电路进行时序分析，然后根据分析的结果，对需要优化的部分进行优化。

时序约束多数情况下集中在一个SDC（Standard Design Constraints）文件，其中包含常见的有：对时钟频率的说明、IO的延迟信息、false_path和multi_cycle_path的说明、以及path_group的指定等等。

综合中的时序分析是静态时序分析，是一种与输入激励无关的，通过遍历所有路径，寻找所有输入组合下电路的最坏延迟情况。最坏延迟的路径称为关键路径。

时序优化把关键路径上的部分或全部电路进行重组或者是替换，来满足时序约束的要求。时序优化通常是在延时和面积上做平衡。同时，已经能满足时序要求的路径，则以优化面积为目标。

7.1 时序约束

绝大部分数字电路是带有工作时钟的同步时序电路。数据的流动应当以一致的步伐进行，即时间脉冲信号每改变一次，数据能够改变一次。这种运作方式是通过同步的数字电路器件，例如触发器来实现的。这类器件以时钟信号为指示，将其输入端的数据复制到其输出端。如图 3.26所示，上述的过程必须满足一定的条件：

建立时间Tsu：在时钟有效沿之前，数据必须保持稳定的最小时间。

保持时间Th：在时钟有效沿之后，数据必须保持稳定的最小时间。

数字电路时钟与数据波形图

这就相当于一个窗口区间，在区间内，数据必须有效并保持稳定。在同步电路中，主要考虑两种时序违例：

• 建立时间违例：时钟信号有效变化之前，如果输入信号没能保持足够长的时间，数据将不能在那个时钟信号变化时被记录下来
• 保持时间违例：时钟信号有效变化之后，如果输入信号没能保持足够长的时间，数据将不能在下一个时钟信号变化时被记录下来
• 时钟频率（或周期）是衡量电路性能的重要指标。因此约束中包含时钟设定（时钟周期，不确定偏斜，波形转换时间，端口，是否为内部时钟等）、输入延迟时间（模块外的寄存器到模块的输入端口的延时）和输出延迟时间（模块输出端口到模块外寄存器的延时）
• 数字电路有很多时序路径，有的路径不需要满足时钟频率的要求，或者有的路径需要多个时钟周期才能完成，这些需要在约束中说明，综合工具会对这些路径做特殊处理。对一般的时序路径，往往会将它们分成不同的集合，分别表示不同的path group；另外，不同的集合可以设置不同的权重；通常情况下权重高的path group会被优先优化。

数字电路的器件存在着驱动能力的限制，因此由设计规则约束来指导综合工具对网表中驱动能力的问题进行修复。时序优化不能产生设计规则违例。时序设计规则有以下几个方面：最大转换时间、最大电容负载、最大扇出。超出设计规则约束的范围可能导致器件负载过大而不能正常工作。这些规则由器件的工艺库lib文件中提供，也可以通过SDC命令设置成更严格的要求。

7.2 时序分析

时序分析中，数字电路首先转换成时序图的形式，再根据时序路径集合的路径进行计算。时序路径的计算根据路径的形式有不同的计算方法。

• 组合逻辑路径：通过逻辑路径的逻辑门延时和信号线延时逐一相加。
• 时序逻辑路径：需要分别计算时序逻辑单元的时钟路径延时和数据信号延时。

根据不同的精度要求和运行时间要求，针对时序图的分析有两种不同的分析策略：

• 基于路径的时序分析：基于时序图找到从起点到终点的所有路径，独立计算每条时序路径的延时。这样能精确地计算每条时序路径，但是随着设计规模的增加，会增加计算量和运行时间
• 基于图的时序分析：基于时序图找到从起点到终点的所有路径，只记录延迟最严重的节点信息，用于下一节点的计算，从而简化了计算规模。

以基于图的时序分析为例，每一个节点需要计算到达时间和需要到达时间：

• 到达时间（Arrival Time，AT）：从起始点到该节点的最长的延时。
• 需要到达时间（Required Arrival Time，RAT）：信号需要保证该节点到端点的最晚时间。

AT和RAT计算

AT和RAT计算是递归的过程，如图所示。根据AT和RAT，二者之差为裕量（Slack），Slack = RAT - AT。

Slack最小的节点组成的路径为关键路径。当Slack为负数时，电路可能存在建立时间违例。

7.3 时序优化

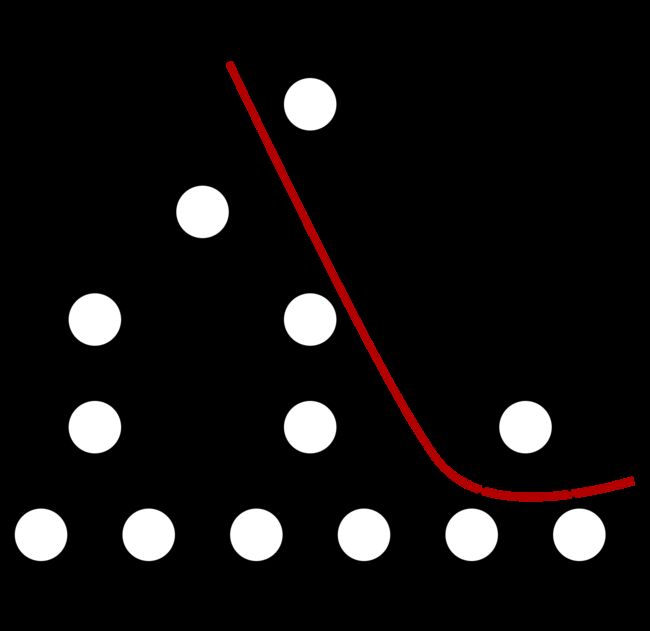
通常情况下，延时和面积是相互制约的两个目标。如下图所示，在单条曲线上，面积最小的电路往往延时比较大，想要达到延时最短，往往需要牺牲面积。综合工具的任务是将曲线尽量往原点（即减少延迟，减小面积）靠近。优化的原则是在给定的约束的情况下，满足时序，并尽量减少面积。

逻辑综合中的时序约束，面积和延迟曲线

 数字电路中常常有运算符逻辑，这些运算符的优化和映射在刚开始的时候由于没有足够的时序信息，往往被实现以及优化成最小面积的逻辑。如果关键路径上有运算逻辑并存在违例，则首先对运算逻辑的实现架构进行调整，可以使用更快的运算架构来减少延迟。以下图加法为例，加法的实现可以是行波进位（ripple carry）结构具有最小面积和最大延迟，也可以是先行进位结构具有较大面积和较小延迟，综合工具根据是否有延时违例来判断选择那种结构。另外，前面介绍的资源共享在E是延迟大的情况下是不合适的，因为原本E只要经过一个多路选择器就可以到达输出；但是在共享以后E要通过多路选择器和乘法器，从而使得延时更长；因此，在这种情况下，综合工具需要重新使用两个乘法器的逻辑结构，尽管会增大面积。

时序优化示例

对于存在违例的关键路径上的普通的组合逻辑单元也可以通过重新优化和映射进行重组使得延时长的信号离输出端更近，从而降低延时。而且根据需要，综合工具可以扁平化消除一部分逻辑层级使得原本在不同模块中的逻辑有机会参与新的优化。另外，逻辑复制，插入缓冲单元，调整大小，重新分配负载等方式均可以改进关键路径的时序延时。

时序优化的过程是不断地优化电路，重新进行时序分析，找到新的关键路径，再优化，循环往复的过程，直到没有延时违例为止或者因为时间关系而终止。对关键路径上的优化常常也将非关键路径的时序也优化了，有时会对没有违例的路径过度优化，这时综合工具需要对这些过度延时优化的路径进行面积和功耗的优化。

一般情况下，时序优化不会跨越寄存器。但有的情况下，比如寄存器的一端有很大的延迟违例，然而另一端有充足的裕量，综合工具可以把一些组合逻辑从高延迟的一端挪到另一端来平衡延时（retiming）。当然这种优化对等价性验证增加了比较大的难度和风险。

时序优化时需要考虑设计规则修正：工艺库中包括每个单元的的设计规则（例如max_capacitance, max_transition和max_fanout)，综合工具可以检查网表是否满足设计规则，如有违例，综合工具可以通过插入缓冲单元（Buffering）和调整大小（Sizing）使用更合适的驱动单元来达到。

---

八、物理逻辑综合

随着工艺技术的不断演进，时序路径中的信号线延迟越来越占有重要的地位。传统的逻辑综合模式下，信号延迟计算被简化为主要跟扇出的数量相关；对于器件的具体物理位置的表达是未知的，不能拿到例如线长、走线的层次等信息，从而影响真实的时序路径的准确计算。物理布局之后的关键路径可能和逻辑综合阶段的关键路径不一样。在这种情况下，综合工具的优化效率会在一定程度被限制。在实际的芯片设计流程中，通常会采取一些过度时序约束的办法使得综合结果网表可以满足布局布线的基本时序要求，但是也带来了其他方面的牺牲。

在physical aware模式下，物理库以及版图信息将被读入，更加精确地时序、面积和功耗信息将可获取，用于指导逻辑优化过程中做出面向物理信息的优化决策，从而减少逻辑综合和物理布局布线之间的鸿沟，并且把后端出现的拥塞问题能提前暴露出来得以解决，从而使得数字实现的迭代次数减少。

首先，综合工具需要扩展数据库使得物理信息能够有效表示；其次，时序分析引擎需要扩展使得时序路径计算充分考虑逻辑单元的位置信息，另外需要完成简单的布局和布线，并依据改进后的时序分析引擎进行时序优化，在优化过程中保持优化后的电路拥有合适的物理信息。

物理信息的引入使得在综合阶段就能了解拥塞状态，并且能够在优化中提供一定的解决办法。综合工具针对连接关系复杂的部分电路可以进行分解降低连接复杂度；在工艺映射时可以采用引脚较少的器件如二选一的选择单元（MUX2）；在门控逻辑优化时根据寄存器的物理位置进行分组使得每个门控单元驱动的寄存器距离接近；在插入扫描链也是根据寄存器的物理位置进行重分组重排序，使得扫描链经过各寄存器的线长大大缩短，避免拥塞的产生。

因此，实现物理逻辑综合需要统一的数据库，一致的延时计算模型，布局布线的引擎。从早期的DCT到现在的Fusion Compiler，物理综合在高性能的设计中发挥越来越重要的作用。

---

总结

逻辑综合工具的技术点包括RTL编译，高阶优化、逻辑优化、工艺映射、逻辑一致性检查、时序优化、Physical-aware综合等，涉及到的技术链条长。 目前的流程是总体上是顺序执行的，每一步的结果都有可能影响后续的流程乃至最终的结果。

综合过程是抽象级别逐步降低的过程：

1. RTL编译生成的通用网表依然保持例如像算术运算符之类的抽象表示
2. 高阶优化是基于通用网表的比较抽象的优化
3. 逻辑优化和工艺映射根据引擎的需要采用工艺无关的数据表示
4. 映射后生成指定工艺的标准门级网表
5. 后期的时序优化和基于物理信息的优化都是在门级网表上进行

综合过程总体来说也是优化粒度降低的过程：

1. RTL编译处理函数调用
2. 循环优化可以对大幅度改变相关的逻辑网表
3. 在高阶优化中处理的是多位位宽的多个运算符的电路
4. 在逻辑优化和工艺映射中处理的单个比特（尽管会同时考虑多个输出比特）的范围较大的组合逻辑锥
5. 后期的时序优化和基于物理信息的优化除基于时序的运算符重新生成以外，所处理的逻辑电路的范围更小，有的优化仅仅改变少数几个门级单元。