【算法】Xgboost原理

【博客地址】：https://blog.csdn.net/sunyaowu315
【博客大纲地址】：https://blog.csdn.net/sunyaowu315/article/details/82905347

  对数据分析、机器学习、数据科学、金融风控等感兴趣的小伙伴，需要数据集、代码、行业报告等各类学习资料，可添加qq群（资料共享群）：102755159，也可添加微信wu805686220，加入微信讨论群，相互学习，共同成长。

---

一 写在前边

开始之前，先立个flag：2019年，抽出时间每月写一篇高质量博文，范围在软件技术、机器学习、风险管理、金融业务理解等，夯实自己的知识面、基础能力、行业认知等。

还是用自己一贯的风格，有了这样一个想法就开始写起来。2019年1月初开始学习，2019年1月14日提笔，随着对XGBoost版块内容理解的加深，不断增删查改，让文章变得逐渐精彩，这篇博文拟定2019年1月末前落笔，加油。

---

二 XGBoost简介

简单介绍：

XGBoost的全称是 Extreme Gradient Boosting。是一个专注于梯度提升算法研究的机器学习函数库，诞生于2014年2月，作者为华盛顿大学研究机器学习的大牛——陈天奇。他在研究中深深的体会到机器学习现有库计算速度慢和精度不够准的问题，为此着手搭建 XGBoost 项目。 XGBoost 学习效果很好，速度也很快。相比梯度提升算法在另一个常用机器学习库scikit-learn中的实现，它的性能经常有十倍以上的提升。问世后，因其优良的学习效果以及高效的训练速度而获得广泛的关注，在各大算法比赛上也大放异彩。

在2018年KDD会议上，作者陈天奇将这一库函数所涉及到的理论推导和加速方法整理为论文发表了出来，尽管这只是一个机器学习方面的函数库，但其中有大量通用的优化加速方法，值得我们学习。为此，我们从原论文出发，结合其他优秀博主博文中精彩的见解，开始本文对XGBoost算法原理的探索。

现在开始：

首先，我们来弄清楚XGBoost在机器学习中所处的位置：

可以看到，在机器学习中，XGBoost属于监督学习中决策树的提升树范畴内（后文有机器学习、监督学习等知识的相关介绍）。

简单说，XGBoost就是用多颗cart决策树通过集成思想搭建的复杂树模型。多颗树如何做预测呢？答案非常简单，就是将每棵树的预测值加总到一起作为最终的预测值，可谓简单粗暴。我们了解过的随机森林RandomForest就是一种依托决策树而建立起来的简单套袋决策相加模型。

为了方便理解，我们用如下一颗CART树和两堆CART树的示例，来判断一个人是否会喜欢计算机游戏：

一棵树： 根据年龄、性别来做判断

两棵树： 树1：年龄、性别；树2：平时是否使用计算机

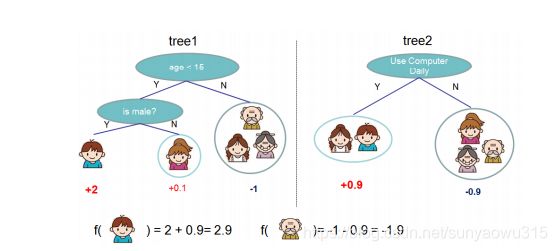
预测值为树1和树2预测值之和。该图表明，我们就是简单将各个CART树的预测分数相加来实现对样本的预测。

！！！蒙了吧！这么多树是怎么选出来的？每棵树的分值又是怎么算出来的？为什么把多棵树分值加和就能作为预测值？效果如何呢？

数学很美，因为它能将很多抽象的事物用漂亮的公式表达出来。——孙耀武 （哈哈哈哈）

现在的树模型，干干巴巴的，麻麻赖赖的，一点儿不圆润！盘它！

接下来我们层层追溯，将XGBoost相关机器学习基础知识点剖析一遍。（方便初学者，高手可直接跳过）

盘的大致顺序为：机器学习——监督学习——决策树——集成学习——XGBoost

过程中会穿插一些像GBDT集成算法以及如今最热门的集成学习提升算法Lightgbm的比对等。

---

三 相关知识

1、机器学习 & 监督学习

机器学习概念很火，其实比较好理解，我们移步机器学习介绍章节：机器学习简介

2、决策树

决策树，很好理解，就是一颗可以帮助决策的分叉树模型。

我们移步决策树原理介绍章节：决策树原理（看罢如果对决策树的原理仍未熟悉的话，多看几遍！多看几遍还不懂的话， 要么是作者功力一般，要么是我们看得还不够）

回到本文，我们已经知道了决策树算法的设计原理：

• 用一些简单的决策规则，根据IF TEHN 逻辑，选择多个特征属性进行分叉，循环多次后成为一个具有一定分类意义的树模型。

3、集成学习

集成学习（ensemble learning），多颗可以帮助决策的树模型组合在一起。

篇幅有限，我们再次移步集成学习原理介绍章节：集成学习原理（如果对集成学习的大致思路仍不了解的话 ，要么。。。。。。要么（手动狗头））

回到本文，我们已经知道了集成学习算法的设计原理：

• 利用一些组合算法的逻辑，通过对弱决策树的组合，生成一个复杂的具有强决策能力的集成树模型。

---

四 XGBoost详解

XGBoost为什么使用CART树而不用其他普通的决策树呢？简单讲，对于分类问题而言，CART树的叶子节点对应的值是一个具体的分数而非类别，这样就特别有利于实现高效的优化算法。

XGBoost出名的原因一是准，二是快，之所以快，其中就有选用CART树的一份功劳。

1、CART树

CART(分类回归树, Class and Regression Tree)是XGBoost最基本的组成部分。其根据训练特征及训练数据构建分类树，判定每条数据的预测结果。其中构建树使用$gini$指数计算增益，即进行构建树的特征选取，$gini$指数公式如下：

$$Gini(D)=\sum _{k=1}^K{p}_k(1-p_k)$$
其中$p_k$表示数据集$D$中类别$k$的概率，$K$表示类别个数。此处的$k$表示分类类别。

$gini$指数计算增益公式如下：

$$Gini(D,A)=\frac{\left|D1\right|}{\left|D\right|}Gini(D1)+\frac{\left|D2\right|}{\left|D\right|}Gini(D2)$$

$D$表示整个数据集，$D_1$和$D_2$分别表示数据集中特征为$A$的数据集和特征非$A$的数据集，$Gini(D_1)$表示特征为$A$的数据集的$gini$指数。

我们以是否打网球为例（只是举个栗子）：

$Gini(D,A_1=“晴”)=\frac{5}{10}\times （\frac{1}{5}\times \frac{4}{5}\times 2）\dotplus \frac{5}{10}\times （\frac{3}{5}\times \frac{2}{5}\times 2）=0.4$

$Gini(D,A_2=“高”)=0.305$

$Gini(D,A_2=“适中”)=0.3$

$Gini(D,A_2=“低”)=0.419$

其中,$Gini(D,A_2="适中")$ 最小，所以构造树首先使用温度适中（我们在决策树篇中说过，$gini$系数和信息增益的不同之处在于：$gini$指数的选择由小到大）。然后分别在左右子树中查找构造树的下一个条件。

本例中，使用温度适中拆分后，子树刚好类别全为是，即温度适中时去打网球的概率为1。

2、Boosting tree

一颗CART往往过于简单,并不能有效地做出预测，为此，采用更进一步的模型boosting tree，利用多棵树来进行组合预测。具体算法如下：

输入：训练集 $N=\left\{(x_1,y_1),(x_2,y_2),\dots (x_n,y_n)\right\}$

输出：提升树 $f_K(x)$

步骤：

• （1）初始化 $f_0(x)=0$

• （2）对 $k=1,2,\dots ,K$

  • ①计算残差 $r_{ki}=y_i-f_{(k-1)}(x_i),i=1,2,\dots ,n$

  • ②拟合残差 $r_{ki}学习一个回归树，得到N(x:{\theta }_k)$

  • ③更新 $f_k(x)=f_{(k-1)}(x)+N(x:{\theta }_k)$

• （3）得到回归提升树： $f_K(x)={\Sigma }_{k=1}^{K}N(x:{\theta }_k)$

不好理解？没事，下面XGBoost有详细的数学推到过程。

3、目标函数

知道了XGBoost是由多个cart组合成的模型，我们就赋予它一个数学表达式，如下所示：

$$\widehat{y_i}=\sum _{k=1}^K{f}_k(x_i),f_k\in F$$

这里的$f$表示一棵具体的$cart$树，$F$表示所有可能的$cart$树，$f(x_i)$就是一棵树的预测值，$\widehat{y_i}$就是这K颗树的预测值加和了。

模型表示出来后，我们自然而然就想问：

• ①这个表达式的参数是什么？
• ②用来优化这些参数的目标函数又是什么？

首先明确下我们的目标，希望建立K个回归树，使得树群的预测值尽量接近真实值（准确率）而且有尽量大的泛化能力（机器学习更为本质的东西），从数学角度看这是一个多目标泛函最优化，看下目标函数（函数的由来可回顾决策树部分，这里不再细说）：
$$L(\varphi )=\sum _i(\widehat{y_i}-y_i)+\sum _k\Omega (f_k)$$

我们看到，这个目标函数同样包含两部分：

• ①第一部分是损失函数，其中i表示第$i$个样本，$l(y^i-yi)$表示第$i$个样本的预测误差，误差越小越好。
• ②第二部分是复杂项，$\sum k\Omega (fk)$表示树的正则项，也就是树的复杂度。该项越小，复杂度越低，泛化能力越强。这里的复杂度为K棵树的复杂度相加。（我们稍后推导：正则项为什么是树的复杂度？）

上面，我们获取了XGBoost模型和它的目标函数，那么训练的任务就是通过最小化目标函数来找到最佳的参数组。

这个模型的目标函数目前看来还比较抽象，接下来我们逐一对其具体化。首先，目标函数的参数在哪里？

我们很自然地想到，XGBoost模型由CART树组成，参数自然存在于每棵CART树之中。那么，就单一的 CART树而言，它的参数是什么呢？

根据上面对CART树的介绍，我们知道，确定一棵CART树需要确定两部分：

• ①树的结构，即如何分裂节点，分裂多少节点。这个结构负责将一个样本映射到一个确定的叶子节点上，其本质上就是一个函数。
• ②就是各个叶子节点上的分数（值）。

叶子节点的分数作为参数是没问题的，但树的结构如何作为参数呢？而且我们有K棵树!怎么确定结构呢？

假设： 如果K棵树的结构都已确定，那么整个模型要关注的就是所有K棵树的叶子节点的值，模型的正则化项就可以设为各个叶子节点值的平方和。此时，整个目标函数就是一个K棵树的所有叶子节点的值的函数，我们就可以使用梯度下降或者随机梯度下降来优化这个目标函数。

但现在树的结构不定，这个假设中用到的办法没用了，必须另寻它法。

4、贪心策略 + 加法训练 + 最优化

通俗解释贪心策略：就是决策时刻按照当前目标最优化决定，说白了就是眼前利益最大化决定，“目光短浅”策略。

所谓加法训练，本质上是一个元算法，适用于所有的加法模型，它是一种启发式算法（boosting相关算法有讲）。运用加法训练，我们的目标不再是直接优化整个目标函数，而是分步优化目标函数。首先优化第一棵树，之后优化第二棵树，依次循环，直至优化完K棵树。整个过程如下所示：

${}^{y_i^{(0)}}=0$

${}^{y_i^{(1)}}=f_1(x_i)=y_i^{(0)}+f_1(x_i)$

${}^{y_i^{(2)}}=f_1(x_i)+f_2(x_i)=y_i^{(1)}+f_2(x_i)$

$...$

${}^{y_i^{(t)}}={\sum }_{k=1}^t{f}_k(x_i)=y_i^{(t-1)}+f_t(x_i)$

在第$t$步时，我们添加了一棵最优的CART树$f_t$，这棵最优的CART树$f_t$是怎么得来的呢？非常简单，就是在现有的$t-1$棵树的基础上，使得目标函数最小的那棵CART树，如下图所示：

$$ob{j}^t=\sum _{i=1}^{n}l(y_i,{\hat{y}}_i^{(t)})+\sum _{i=1}^t\Omega (f_i)$$

$$=\sum _{i=1}^{n}l(y_i,{\hat{y}}_i^{(t-1)}+f_t(x_i))+\Omega (f_t)+constant$$

$constant$就是前$t-1$棵树的复杂度。

假如我们使用的损失函数是$MSE$，那么上述表达式会变成这个样子：

$$ob{j}^t=\sum _{i=1}^n(y_i-({\hat{y}}_i^{(t-1)}+f_t(x_i)){)}^2+\sum _{i=1}^t\Omega (f_i)$$

$$=\sum _{i=1}^n[2({\hat{y}}_i^{(t-1)}-y_i)f_t(x_i)+f_t(x_i{)}^2]+\Omega (f_t)+constant$$

这个式子非常漂亮，因为它含有$f_t(x_i)$的一次式和二次式，而且一次式项的系数是残差，这会对我们后续的优化提供很多方便。

注意：$f_t(x_i)$其实就是$f_t$的某个叶子节点的值。之前我们提到过，CART树中，叶子节点的值可以作为模型的参数。

但是对于其他损失函数，我们未必能得出如此漂亮的式子。所以，对于一般的损失函数，我们需要将其作泰勒二阶展开，如下所示：

$$ob{j}^t=\sum _{i=1}^n[l(y_i,{\hat{y}}_i^{(t-1)})+gi{f}_t(x_i)+\frac{1}{2}hi{f}_t^2(x_i)]+\Omega (f_t)+constant$$

其中：
$$gi={\partial }_{\widehat{y^{t-1}}}l(y_i,{\hat{y}}_i^{(t-1)})$$
$$hi={\partial }_{\widehat{y^{t-1}}}^{2}l(y_i,{\hat{y}}_i^{(t-1)})$$

这里明确下$gi$和$hi$的含义：

现有$t-1$棵树，这$t-1$棵树组成的模型对第$i$个训练样本有一个预测值$y^i$，这个$y^i$与真实标签$yi$肯定有一定的差距，而这个差距可以用$l(yi,y^i)$这个损失函数来衡量。gi和hi的就是对这个损失函数的梯度和二阶梯度。

来看一个具体的例子，假设我们正在优化第11棵CART树，也就是说前10棵CART树已经确定了。这10棵树对样本$(x_i,y_i=1)$的预测值是$y^i=-1$，假设我们现在是做分类，损失函数是：

$$L(\theta )=\sum _i[y_{i}ln(1+e^{-\widehat{y_i}})+(1-y_i)ln(1+e^{\widehat{y_i}})]$$

在$y_i=1$时，损失函数变为：

$$ln(1+e^{-\widehat{y_i}})$$

我们可以求出这个损失函数对于y^i的梯度，如下所示：

$$\frac{1}{1+e^{-\widehat{y_i}}}(e^{-\widehat{y_i}})\ast (-1)=\frac{-e^{-\widehat{y_i}}}{1+e^{-\widehat{y_i}}}$$

将$y^i=-1$代入上面的式子，计算得到-0.27。这个-0.27就是$g_i$。该值为负，也就是说，如果我们想要减小这10棵树在该样本点上的预测损失，就应该沿着梯度的反方向走，也就是要增大$y^i$的值,使其趋向于正，因为$y_i=1$就是正的。

若$N$是训练样本的数量，那么在优化第$t$棵树时，就各有$N$个$gi$和$hi$要计算。如果有10万样本，在优化第t棵树时，就需要计算出个10万个$gi$和$hi$。XGBoost的并行运算能力正好可以解决这种庞大复杂的计算工作。

好，现在我们来审视下这个式子，哪些是常量，哪些是变量。式子最后有一个$constant$项就是前$t-1$棵树的正则化项。$l(yi,y{i}^t-1)$也是常数项。剩下的三个变量项分别是第$t$棵CART树的一次式，二次式，和整棵树的正则化项。再次提醒，这里所谓的树的一次式，二次式，其实都是某个叶子节点的值的一次式，二次式。

我们的目标是让这个目标函数最小化，常数项显然没有什么用，把它们去掉就变成了下面这样：

$$\sum _{i=1}^n[gi{f}_t(x_i)+\frac{1}{2}hi{f}_t^2(x_i)]+\Omega (f_t)$$

因为这些一次式和二次式的系数是$gi$和$hi$，而$gi$和$hi$可以并行地求出来。而且，$gi$和$hi$不依赖于损失函数的形式，只要这个损失函数二次可微就可以。这有什么好处呢？我们可以自定义损失函数，只需满足二次可微即可。

5、正则项

现在就剩后面的$\Omega (ft)$了。我们来定义下如何衡量一棵树的正则化项。这个事儿并没有一个客观的标准，可以见仁见智。为此，我们先对CART树作另一番定义，如下所示：

那么复杂度的表达式可以表示为 ：

$$f_t(x)={\omega }_{q(x)},\omega \in R^T,q:R^d\to \left\{1,2,3....,T\right\}$$

需要解释下这个定义，首先，一棵树有$T$个叶子节点，这$T$个叶子节点的值组成了一个$T$维向量$w$，$q(x)$是一个映射，用来将样本映射成$1$到$T$的某个值，也就是把它分到某个叶子节点，$q(x)$其实就代表了CART树的结构。$w_q(x)$自然就是这棵树对样本$x$的预测值了。

有了这个定义，XGBoost就使用了如下的正则化项：

$$\Omega （f）=\gamma T,\frac{1}{2}\lambda \sum _{j=1}^T{\omega }_j^2$$

注意：这里出现了$\gamma$和$\lambda$，这是XGBoost自己定义的，在使用XGBoost时，你可以设定它们的值，显然，$\gamma$越大，表示越希望获得结构简单的树，因为此时对较多叶子节点的树的惩罚越大。$\lambda$越大也是越希望获得结构简单的树。

为什么XGBoost要选择这样的正则化项？很简单，好使！效果好才是真的好。

至此，我们关于第t棵树的优化目标已然很清晰，下面我们对它做如下变形，请睁大双眼，集中精力：

$$ob{j}^t\approx \sum _{i=1}^n[gi{\omega }_{q(x)}+\frac{1}{2}hi{\omega }_{q(x)}^2]+\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{\omega }_j^2$$

$$=\sum _{i=1}^T[(\sum _{i\in Ij}gi){\omega }_j+\frac{1}{2}(\sum _{i\in Ij}hi+\lambda ){\omega }_j^2]+\gamma T$$

这里需要停一停，认真体会下。$Ij$代表什么？它代表一个集合，集合中每个值代表一个训练样本的序号，整个集合就是被第$t$棵CART树分到了第$j$个叶子节点上的训练样本。理解了这一点，再看这步转换，其实就是内外求和顺序的改变。

进一步，我们可以做如下简化：

$$ob{j}^t=\sum _{i=1}^T[G_i{\omega }_i+\frac{1}{2}(H_j+\lambda ){\omega }_j^2]+\gamma T$$

其中的$Gj$和$Hj$就是简化后损失函数的梯度和二阶梯度

对于第$t$棵CART树的某一个确定的结构（可用$q(x)$表示），所有的$Gj$和$Hj$都是确定的。而且上式中各个叶子节点的值$wj$之间是互相独立的。上式其实就是一个简单的二次式，我们很容易求出各个叶子节点的最佳值以及此时目标函数的值。如下所示：

$${\omega }_j^{\ast }=-\frac{G_I}{H_i+\lambda }$$

$$ob{j}^{\ast }=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T$$

$obj\ast$代表了什么呢？

它表示了这棵树的结构有多好，值越小，代表这样结构越好！也就是说，它是衡量第$t$棵CART树的结构好坏的标准。

注意，这个值仅仅是用来衡量结构的好坏的，与叶子节点的值可是无关的。为什么？请再仔细看一下$ob{j}^{\ast }$的推导过程。$ob{j}^{\ast }$只和$Gj$和$Hj$和$T$有关，而它们又只和树的结构$(q(x))$有关，与叶子节点的值可是半毛关系没有。如下图所示：

这里，我们对$w{\ast }_j$给出一个直觉的解释，以便能获得感性的认识。我们假设分到j这个叶子节点上的样本只有一个。那么，$w{\ast }_j$就变成如下这个样子：

$${\omega }_j^{\ast }=(\frac{1}{H_i+\lambda })\ast (-gi)$$

$\frac{1}{H_i+\lambda }$是学习率，$(-gi)$是反向的梯度

这个式子告诉我们，$w{\ast }_j$的最佳值就是负的梯度乘以一个权重系数，该系数类似于随机梯度下降中的学习率。观察这个权重系数，我们发现，$h_j$越大，这个系数越小，也就是学习率越小。$h_j$越大代表什么意思呢？代表在该点附近梯度变化非常剧烈，可能只要一点点的改变，梯度就从10000变到了1，所以，此时，我们在使用反向梯度更新时步子就要小而又小，也就是权重系数要更小。

6、树结构

好了，有了评判树结构好坏的标准，我们就可以先求最佳的树结构，这个定出来后，最佳的叶子结点的值实际上在上面已经求出来了。

问题是： 树的结构近乎无限多，一个一个去测算它们的好坏程度，然后再取最好的显然是不现实的。所以，我们仍然需要采取贪心策略，就是逐步学习出最佳的树结构。这与我们将K棵树的模型分解成一棵一棵树来学习是一个道理，只不过从一棵一棵树变成了一层一层节点而已。看下具体学习过程：

以上文提到过的判断一个人是否喜欢计算机游戏为例子。最简单的树结构就是一个节点的树。可以算出这棵单节点的树的好坏程度$ob{j}^{\ast }$。假设现在想按照年龄将这棵单节点树进行分叉，我们需要知道：

• ①按照年龄分是否有效，也就是是否减少了$ob{j}^{\ast }$的值

• ②如果可分，那么以哪个年龄值来分。

为了回答上面两个问题，我们可以将这一家五口人按照年龄做个排序。如下图所示：

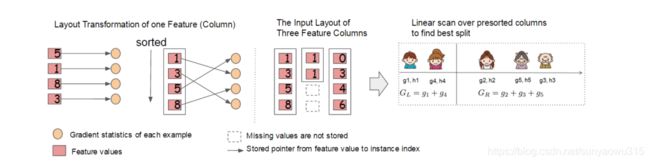
按照这个图从左至右扫描，我们就可以找出所有的切分点。对每一个确定的切分点，我们衡量切分好坏的标准如下：

$$Gain=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }]-\gamma$$

这个$Gain$实际上就是单节点的$ob{j}^{\ast }$减去切分后的两个节点的树$ob{j}^{\ast }$，$Gain$如果是正的，并且值越大，表示切分后$obj\ast$越小于单节点的$ob{j}^{\ast }$，就越值得切分。同时，我们还可以观察到，$Gain$的左半部分如果小于右侧的$\gamma$，则$Gain$就是负的，表明切分后$ob{j}^{\ast }$反而变大了。$\gamma$在这里实际上是一个临界值，它的值越大，表示我们对切分后$obj$下降幅度要求越严。这个值也是可以在XGBoost中设定的。

扫描结束后，我们就可以确定是否切分，如果切分，对切分出来的两个节点，递归地调用这个切分过程，我们就能获得一个相对较好的树结构。

接下来，继续分裂，按照上述的方式，形成一棵树，再结合建树过程中的加法训练形成第二棵树，之后循环，每次在上一次的预测基础上取最优进一步分裂/建树，这就是这个XGBoost算法贪心策略的核心！

凡是这种循环迭代的方式必定有停止条件，什么时候停止呢：

• ①当节点引入的分裂带来的增益小于一个阀值的时候，停止分裂，我们可自定义一个参数设置；
• ②当树达到最大深度时则停止建立决策树，设置一个超参数max_depth，防止过拟合；
• ③当样本权重和小于设定阈值时则停止建树，这涉及到一个超参数-最小的样本权重和min_child_weight，就是一个叶子节点样本太少了，也终止，同样防止过拟合；

注意： XGBoost的切分操作和普通的决策树切分过程是不一样的。普通的决策树在切分的时候并不考虑树的复杂度，而依赖后续的剪枝操作来控制。XGBoost在切分的时候就已经考虑了树的复杂度，就是那个$\gamma$参数。所以，它不需要进行单独的剪枝操作（当然XGBoost支持后剪枝）。

7、XGBoost算法特点

看下XGBoost的一些重点：

• ①$\omega$是最优化求出来的，不是啥平均值或规则指定的，这个算是一个思路上的新颖吧。传统GBDT以CART作为基分类器，XGBoost还支持线性分类器，这个时候XGBoost相当于带L1和L2正则化项的逻辑斯蒂回归（分类问题）或者线性回归（回归问题）。传统GBDT在优化时只用到一阶导数信息，XGBoost则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数。顺便提一下，XGBoost工具支持自定义代价函数，只要函数可一阶和二阶求导。
• ②正则化项过拟合；
• ③支持自定义损失函数；
• ④支持并行化。boosting技术中下一棵树依赖上述树的训练和预测，所以树与树之间应该是只能串行！哪里可以并行？没错，同层级节点可并行。具体对于某个选择最佳分裂点，候选分裂点计算增益用多线程并行。（据说恰好这个也是树形成最耗时的阶段），训练效率高！
• ⑤可实现后剪枝；
• ⑥交叉验证，方便选择最好的参数，early stop，比如你发现30棵树预测已经很好了，不用进一步学习残差了，那么停止建树；
• ⑦行采样、列采样，随机森林的套路（防止过拟合），不仅能降低过拟合，还能减少计算；
• 对缺失值的处理。对于特征的值有缺失的样本，XGBoost可以自动学习出它的分裂方向；
• ⑧支持设置样本权重，这个权重体现在梯度$gi$和二阶梯度$hi$上，是不是有点adaboost的意思，重点关注某些样本。XGBoost在进行完一次迭代后，会将叶子节点的权重乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间。实际应用中，一般把eta设置得小一点，然后迭代次数设置得大一点。
• ⑨对缺失值的处理。XGBoost还特别设计了针对稀疏数据的算法， 假设样本的第i个特征缺失时，无法利用该特征对样本进行划分，这里的做法是将该样本默认地分到指定的子节点，至于具体地分到哪个节点还需要某算法来计算。
  算法的主要思想是，分别假设特征缺失的样本属于右子树和左子树，而且只在不缺失的样本上迭代，分别计算缺失样本属于右子树和左子树的增益，选择增益最大的方向为缺失数据的默认方向（咋一看如果缺失情况为3个样本，那么划分的组合方式岂不是有8种？指数级可能性啊，仔细一看，应该是在不缺失样本情况下分裂后（有大神的请确认或者修正），把第一个缺失样本放左边计算下loss function和放右边进行比较，同样对付第二个、第三个…缺失样本，这么看来又是可以并行的？？）。

8、XGBoost工程优化

• ①Column Block for Parallel Learning
  总的来说：按列切开，升序存放；
  方便并行，同时解决一次性样本读入炸内存的情况

• ②由于将数据按列存储，可以同时访问所有列，那么可以对所有属性同时执行split finding算法，从而并行化split finding（切分点寻找）-特征间并行
  可以用多个block(Multiple blocks)分别存储不同的样本集，多个block可以并行计算-特征内并行

• ③Blocks for Out-of-core Computation
  数据大时分成多个block存在磁盘上，在计算过程中，用另外的线程读取数据，但是由于磁盘IO速度太慢，通常更不上计算的速度，
  将block按列压缩，对于行索引，只保存第一个索引值，然后只保存该数据与第一个索引值之差(offset)，一共用16个bits来保存 offset，因此，一个block一般有216216个样本。

五 调参技巧 & 代码实现

1、Gradient Boosting的调参

Tree-Specific Parameters

• min_samples_split：对一个节点劈裂的条件之一就是该节点包含样本数大于min_samples_split。该值过高则可能过拟合，过小则欠拟合。
• min_samples_leaf：叶节点包含的最少样本数。参数目的同min_samples_split。通常训练集中类不均衡时，该值需要设置小点，以防止小类被大类覆盖。
• min_weight_fraction_leaf：同min_samples_leaf，只不过改成叶节点包含样本数量占总样本的比例下限。两者仅设其一。
• max_depth: 树的最大深度，不容易调整，通常要采用CV(cross validate)方式。
• max_leaf_nodes: 叶节点最大数量。作用同最大深度。两者仅设其一。
• max_features： 寻找最优切分点时，考虑的最大特征的个数。随机选取。经验规则是设为总特征数量的开方，但在调参过程中考虑总数的30%-40%范围。该超参设置过高可能导致过拟合。

Boosting Parameters

• learning_rate：确定了每棵基本树的输出结果在最终结果中的影响权重。通常较小的值使得模型鲁棒性更好，但需要更多的基本树，导致计算量较大。
• n_estimators：基本基本树的个数。
• subsample：从总的训练数据集中挑选样本的比例，以构建某个基本树的专有的训练数据集。通常设置为0.8。

Miscellaneous Parameters

• loss: 损失函数。通常默认的效果不错。
• init: 将已有的决策树设为基本树。
• warm_start：设置为True则表示可以借用前面已经训练好的基本树训练接下来添加的基本树。合理设置可以加快训练速度。

调参过程

参考资料2中，Aarshay分享了他的调参经验，核心的思想是先调节影响最大的参数，再调节次要的参数。

• 设置较大的learning_rate以及相应的最优n_estimator
• 调节Tree-Specific Parameters
• 调节max_depth以及min_samples_split
• 调节min_samples_leaf
• 调节max_features
• 降低learning_rate，并相应地增加n_estimator

2、XGBoost的调参

• general parameters：使用何种基本模型。通常是决策树或线性模型。
• booster parameters：基本树必需的超参数。
• gamma: 正则化项T前系数。
• reg_lambda: L2正则化项前系数。
• reg_alpha：L1正则化项前系数。
• min_child_weight ：节点包含样本的权重之和的下限。即如果某个节点所有样本的权重之和低于该值，则不劈裂。其作用类似于GB的min_samples_leaf。
• colsample_bytree：构建某棵基本树时，从所有特征中随机抽取特征数量比例。
• colsample_bylevel: 选择最优切分点时，考虑的特征数量所占比例。其作用类似于GB中的max_features。
  其他参数参考GB。
• task parameters：学习过程必须的超参数。目标函数形式、模型评价标准等。

调参过程

参考GB的调参过程。对于XGBoost, max_depth、min_child_weight以及gamma是影响基本树预测准确率最为重要的三个因素。

# 实现XGBoost回归, 以MSE损失函数为例
import numpy as np


class Node:
    def __init__(self, sp=None, left=None, right=None, w=None):
        self.sp = sp  # 非叶节点的切分，特征以及对应的特征下的值组成的元组
        self.left = left
        self.right = right
        self.w = w  # 叶节点权重，也即叶节点输出值

    def isLeaf(self):
        return self.w


class Tree:
    def __init__(self, _gamma, _lambda, max_depth):
        self._gamma = _gamma  # 正则化项中T前面的系数
        self._lambda = _lambda  # 正则化项w前面的系数
        self.max_depth = max_depth
        self.root = None

    def _candSplits(self, X_data):
        # 计算候选切分点
        splits = []
        for fea in range(X_data.shape[1]):
            for val in X_data[fea]:
                splits.append((fea, val))
        return splits

    def split(self, X_data, sp):
        # 劈裂数据集，返回左右子数据集索引
        lind = np.where(X_data[:, sp[0]] <= sp[1])[0]
        rind = list(set(range(X_data.shape[0])) - set(lind))
        return lind, rind

    def calWeight(self, garr, harr):
        # 计算叶节点权重，也即位于该节点上的样本预测值
        return - sum(garr) / (sum(harr) + self._lambda)

    def calObj(self, garr, harr):
        # 计算某个叶节点的目标(损失)函数值
        return (-1.0 / 2) * sum(garr) ** 2 / (sum(harr) + self._lambda) + self._gamma

    def getBestSplit(self, X_data, garr, harr, splits):
        # 搜索最优切分点
        if not splits:
            return None
        else:
            bestSplit = None
            maxScore = -float('inf')
            score_pre = self.calObj(garr, harr)
            subinds = None
            for sp in splits:
                lind, rind = self.split(X_data, sp)
                if len(rind) < 2 or len(lind) < 2:
                    continue
                gl = garr[lind]
                gr = garr[rind]
                hl = harr[lind]
                hr = harr[rind]
                score = score_pre - self.calObj(gl, hl) - self.calObj(gr, hr)  # 切分后目标函数值下降量
                if score > maxScore:
                    maxScore = score
                    bestSplit = sp
                    subinds = (lind, rind)
            if maxScore < 0:  # pre-stopping
                return None
            else:
                return bestSplit, subinds

    def buildTree(self, X_data, garr, harr, splits, depth):
        # 递归构建树
        res = self.getBestSplit(X_data, garr, harr, splits)
        depth += 1
        if not res or depth >= self.max_depth:
            return Node(w=self.calWeight(garr, harr))
        bestSplit, subinds = res
        splits.remove(bestSplit)
        left = self.buildTree(X_data[subinds[0]], garr[subinds[0]], harr[subinds[0]], splits, depth)
        right = self.buildTree(X_data[subinds[1]], garr[subinds[1]], harr[subinds[1]], splits, depth)
        return Node(sp=bestSplit, right=right, left=left)

    def fit(self, X_data, garr, harr):
        splits = self._candSplits(X_data)
        self.root = self.buildTree(X_data, garr, harr, splits, 0)

    def predict(self, x):
        def helper(currentNode):
            if currentNode.isLeaf():
                return currentNode.w
            fea, val = currentNode.sp
            if x[fea] <= val:
                return helper(currentNode.left)
            else:
                return helper(currentNode.right)

        return helper(self.root)

    def _display(self):
        def helper(currentNode):
            if currentNode.isLeaf():
                print(currentNode.w)
            else:
                print(currentNode.sp)
            if currentNode.left:
                helper(currentNode.left)
            if currentNode.right:
                helper(currentNode.right)

        helper(self.root)


class Forest:
    def __init__(self, n_iter, _gamma, _lambda, max_depth, eta=1.0):
        self.n_iter = n_iter  # 迭代次数，即基本树的个数
        self._gamma = _gamma
        self._lambda = _lambda
        self.max_depth = max_depth  # 单颗基本树最大深度
        self.eta = eta  # 收缩系数, 默认1.0,即不收缩
        self.trees = []

    def calGrad(self, y_pred, y_data):
        # 计算一阶导数
        return 2 * (y_pred - y_data)

    def calHess(self, y_pred, y_data):
        # 计算二阶导数
        return 2 * np.ones_like(y_data)

    def fit(self, X_data, y_data):
        step = 0
        while step < self.n_iter:
            tree = Tree(self._gamma, self._lambda, self.max_depth)
            y_pred = self.predict(X_data)
            garr, harr = self.calGrad(y_pred, y_data), self.calHess(y_pred, y_data)
            tree.fit(X_data, garr, harr)
            self.trees.append(tree)
            step += 1

    def predict(self, X_data):
        if self.trees:
            y_pred = []
            for x in X_data:
                y_pred.append(self.eta * sum([tree.predict(x) for tree in self.trees]))
            return np.array(y_pred)
        else:
            return np.zeros(X_data.shape[0])


if __name__ == '__main__':
    from sklearn.datasets import load_boston
    from sklearn.model_selection import train_test_split
    from sklearn.metrics import mean_absolute_error
    import matplotlib.pyplot as plt

    boston = load_boston()
    y = boston['target']
    X = boston['data']
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
    f = Forest(50, 0, 1.0, 4, eta=0.8)
    f.fit(X_train, y_train)
    y_pred = f.predict(X_test)
    print(mean_absolute_error(y_test, y_pred))
    plt.scatter(np.arange(y_pred.shape[0]), y_test - y_pred)
    plt.show()

六 项目实战

• XGBoost算法构建信用评分卡模型

七 关键词

• 决策树cart
• 信息增益
• 基尼系数
• 分类误差（分类树）
• 均方误差（回归树）
• 贪心策略
• 加法训练
• 目标函数
• 损失函数
• 正则项
• 泰勒展开
• 样本节点
• 交叉验证
• 预剪枝
• 并行处理
• 高度灵活性

八 结尾

XGBoost和深度学习的关系，陈天奇在Quora上的解答如下：
不同的机器学习模型适用于不同类型的任务。深度神经网络通过对时空位置建模，能够很好地捕获图像、语音、文本等高维数据。而基于树模型的XGBoost则能很好地处理表格数据，同时还拥有一些深度神经网络所没有的特性（如：模型的可解释性、输入数据的不变性、更易于调参等）。

这两类模型都很重要，并广泛用于数据科学竞赛和工业界。举例来说，几乎所有采用机器学习技术的公司都在使用tree boosting，同时XGBoost已经给业界带来了很大的影响。

参考：

• 陈天奇原始论文
• Opencv2.4.9源码分析——Decision Trees
• 通俗、有逻辑的写一篇说下XGBoost的原理，供讨论参考
• XGBoost简介
• XGBoost原理解析
• XGBoost的原理没你想像的那么难
• 机器学习算法中 GBDT 和 XGBoost 的区别有哪些？
• XGBoost算法简介及Python实现
• XGBoost参数调优
• [机器学习]集成学习–bagging、boosting、stacking

---

好了，现在是2019年1月23日，憋了将近20天，从逻辑，到算法，再到细节，终于拿下。2019年我与机器学习算法的厮杀之2月再见。

作为一个半路出家的小学生，补充一句：

数学真美。