图神经网络入门

图神经网络入门 – 潘登同学的GNN笔记

图神经网络是如何工作的

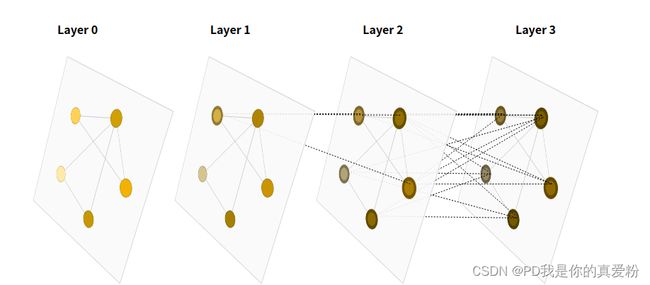
注意 上图的的传递方向是Layer3 -> Layer 0, 所以一个节点的信息是由上一层中与他相邻的(包括自己)节点一起贡献的信息；

图的回顾

图是表示实体之间关系的数据结构，点就是实体，边就是关系

用向量来表示图， 将图的顶点、图的边、整个图用向量来表示，举个例子

• 可以用一个6维的向量来表示顶点
• 用8维的向量来表示边
• 用5维的向量来表示整个图

问题就在于如何表示，这样的表示能否反映真实情况…

将图片表示成图

在概率图模型中也见到过，就是将相邻的像素点连一条边，构造一个图，举个例子

如上图所示，第一行第二列的像素点与其8个方向的相邻像素点连接了一条边；中间的那个就是邻接矩阵了；

将文本表示为图

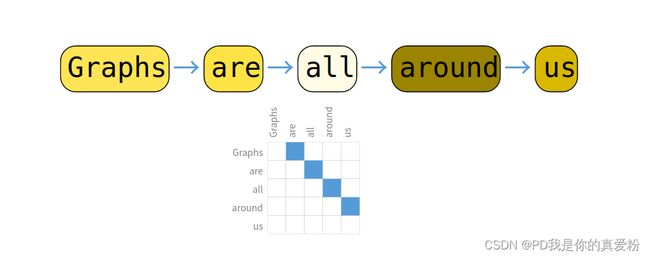
如上图所示，一个词与其下一个词连一条又向边， 一整句话构成一个有向无环图；

将分子结构表示成图

将社交网络表示成图

下图表示了生活中常见到的图的规模，包括社交网络图、分子图、论文引用图、维基百科的引用图；

在神经网络中表示图

• 节点： 可以将第$i$个节点(因为每个节点是一个向量)存储在矩阵的第$i$行中
• 边： 可以将第$i$条边(因为每条边一个向量)存储在矩阵的第$i$行中
• 全局： 就是一个向量
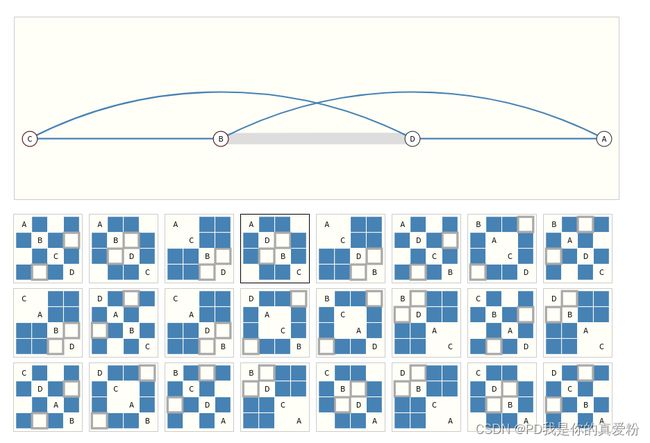
• 连接性： 因为邻接矩阵占用空间很大，而且对于一个图，有很多中邻接矩阵(因为调换节点顺序不改变邻接矩阵)；稀疏矩阵不便于计算; 所以采用的是邻接表的形式，对于从节点$i$到节点$j$的边，放到邻接表中就利用$(i,j)$表示,表的数据与邻接表各个元组的数据一一对应；

下图则是用标量来表示点和边(当然可以换成向量), 用邻接表来存储边；

三种任务

图层面的任务

举了例子，比如要判断一个图中是否存在两个环

这类似于 MNIST 和 CIFAR 的图像分类问题，我们希望将标签与整个图像相关联。 对于文本，一个类似的问题是情绪分析，我们希望一次识别整个句子的情绪或情绪。

节点层面的任务

节点级任务与预测图中每个节点的身份或角色有关，举个例子，比如要判断一部剧Zach’s karate club，两个教练起了分歧，他们的学员站队的问题；

按照图像类比，节点级预测问题类似于图像分割，我们试图标记图像中每个像素的作用。 对于文本，类似的任务是预测句子中每个单词的词性（例如名词、动词、副词等）。

边层面的任务

边表达的是节点之间的关系，对于图像来说，就是实体与实体之间的关系，举个例子

我们做完语义分割之后，想知道实体之间的关系，如上图中两个人就是对手关系，一个人正在踢另一个人，而还有一个人则是裁判，他们都站在擂台上，剩下后面的人都在注视着两个选手的比赛；

GNN的结构

GNN的定义： GNN是对图的所有属性(节点、边、全局上下文)的可优化转换，它保留了图的对称性(排列不变性，对称信息指的是将顶点进行另外一种排序信息之后，整个结果不会发生改变）

GNN的假设： 保持了图的对称性

(这里补充一下CNN、RNN的假设， CNN的假设是空间变换的不变性， RNN假设的是时间的延续性)

GNN的信息在各层间的传递使用的是 message passing（信息传递神经网络，GNN也可以用别的神经网络来进行描述，这个地方用的是信息传递的框架）

GNN的输入是图，输出也是图，它会对顶点、边和全局的向量进行变换，但是不会改变图的连接性（顶点和边的连接信息在进入图神经网络之后是不会改变的）

构造一个最简单的GNN

如下图所示，对于顶点向量、边向量和全局向量分别构造MLP（多层感知机），MLP的输入大小和输出大小相同，取决于输入的向量

• $f_{U_x}$： 表示全局的MLP
• $f_{V_x}$： 表示顶点的MLP
• $f_{E_x}$： 表示边的MLP
• 这三个MLP组成了GNN的层。这个层的输入是图，输出还是图，如下图所示，它的作用是：对于顶点的向量、边的向量和全局的向量分别找到对应的MLP，然后将它们放进去得到它们的输出，作为其对应的更新，图进去再出来之后的属性都是被更新过的，但是整个图的结构没有发生变化（只对属性集变化，但是不改变图的结构）

检验一下是否满足GNN的定义

• 因为MLP是对每个向量独自作用的而不会考虑所有的连接信息，所以不管对整个顶点做任何排序信息都不会改变结果
• 所以这个最简单的层就满足了之前的两个要求，也可以将这些层叠加在一起构造成比较深的GNN

顶点分类任务

和一般的神经网络没有太多区别，因为顶点已经表示成向量了，然后要对它做预测的话，比如前述的空手到俱乐部的问题，其实就是一个简单的二分类问题

每个顶点都有了对应的向量表示，接一层sigmoid就能得到二分类结果，如果是多类别的话，就接一层softmax…

缺失数据预测

如果我们没有某个点的向量表示、如果我们没有某条边的向量表示、如果我们没有全局的表示；我们可以采用一个pooling的技术来获得他们的表示；

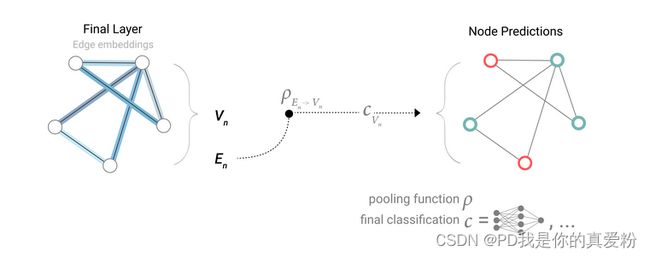
对于某个顶点来说，需要将与其连接的那些边和全局的向量拿出来，加和(可以是求平均，可以是求最大),最后再经过update function， 得到下一层的该点的向量表示；如图所示

整体表示如图

同理可以利用顶点和全局对边做预测

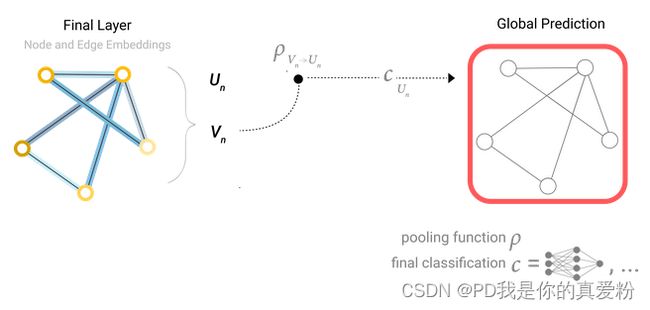
也可以利用顶点对全局信息做预测

总结上面的内容，就能得到一个简单的GNN，如下图所示

• 给定一个输入图，首先进入一系列的GNN层（每个层里面有三个MLP，对应三种不同的属性），会得到一个保持整个图结构的输出（但是里面所有的属性已经进行了更新）
• 最后根据所要预测的属性添加合适的输出层
• 但如果缺失信息的话可以加入合适的汇聚层就可以完成预测了
• 这是最简单的情况。虽然这个情况很简单，但是有很大局限性，主要的问题在于在GNN块中并没有使用图的结构信息（对每个属性做变换的时候，仅仅是每个属性进入自己对应的MLP，并没有体现出三者之间的相互联系的连接信息），导致并没有合理地把整个图的信息更新到属性里面，以至于最后的结果并不能够特别充分利用图的信息

在GNN中加入信息传递

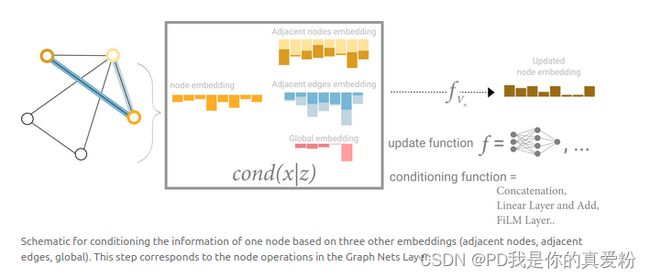
当将信息从当前层向下一层传递的时候， 利用图的结构进行传递， 如图所示

• 首先将要某点想了与其相邻顶点的向量加在一起得到汇聚的向量(聚合步)
• 再将这个汇聚的向量放进MLP得到该顶点向量的更新(更新步)

这是一个最简单形式的信息传递， 这个跟标准的图片上的卷积有点类似，等价于在图片上做卷积，但是卷积核窗口里面每个窗口的权重是要相同的（因为在卷积里面其实是每一个顶点和它邻居顶点的向量会做加权和，权重来自于卷积窗口），这里没有加权和，只是加，所以权重应该是一样的，但是通道还是保留了（卷积中有多输入通道和多输出通道，对应信息传递过程中MLP还是保留了），所以和卷积操作有点类似，但是还是有区别；

GNN层也可以通过堆叠来完成整个图的长距离信息传递过程。

下图表示一个顶点，顶点之间通过距离为1的邻居（一近邻）将它的信息传递过来，表示从 $v$ 到 $v$ 的汇聚过程，这也是最简单的信息传递的过程

再复杂一点，之前考虑过，假设缺失某种属性，可以从别的属性汇聚过来，以弥补这个属性，同理，不需要等到最后一层在进行汇聚，可以在较早的时候在边和顶点之间汇聚信息, 下图展示了如何将顶点的信息传递给边，然后再把边的信息传递给顶点

• 首先通过ρ（V to E）把顶点的向量传递给边（把每个边连接的顶点信息加到边的向量中，假设维度不一样的话，会先做投影，投影到同样的维度然后再加进去，这样边就拿到了顶点的信息）
• 同样可以每个顶点可以把连接它的边的信息也加到自己上面，同样维度不同的话，可以先做投影（这里如果维度不一样的话，会做两次投影），维度一样的可以直接相加
• 另外也可以将它contact在一起，也就是并在一起（类似于矩阵的拼接操作）
• 这样就完成了顶点到边的传递、边到顶点的传递之后，再进入到各自的MLP做更新

这里是先把顶点的信息传递给边做更新，然后再把更新过信息的边的信息汇聚到顶点再做更新，如下图右图所示。如果反过来的话会得到不一样的结论如下图左图所示

• 之前顶点和边之间不交换任何信息，各自进行更新，所以谁先进行更新不影响
• 但是现在先更新顶点还是先更新边会导致不一样的结果，目前来说还没有一致的结论说说先更新谁比较好，只是说这两种会导致不一样的结果
• 其实可以交替更新，如上图下半部分所示：同时顶点汇聚到边然后边汇聚到顶点，汇聚之后先不要相加，然后再回来一次，就相当于两边的信息都有了，等价于两个信息同时汇聚，最终向量可能会宽一点，这样就不用担心到底是先做谁的汇聚了

全局信息的作用

之前有一个问题：因为每次只去看自己的邻居，假设图比较大而且连接没那么紧密的时候，会导致信息从一个点传递到一个很远的点需要走很长的步

解决方案：加入master node（或者叫context vector），这个点是虚拟的点，可以跟所有的顶点相连，也可以跟所有的边相连（这里在图上面不好说，因为一个顶点是没办法跟边相连的，在这里是一个抽象的概念），它其实就是U(全局信息)，U跟所有的V里面的东西是相连的，跟E里面所有的东西也是相连的，所以如果想要把顶点的信息汇聚给边的时候，也会把U汇聚过来，因为U跟边是相连的（同理，汇聚顶点的时候，也会把U和它相连的E连过来），最后自己更新U的时候，会把所有的顶点信息和边的信息都拿过来，最后完成汇聚再做更新;

到此，这三类属性都学到了对应的向量，而且这些向量在早期就已经进行了大量的信息传递，最后在做预测的时候就可以只用本身的向量，也可以把相邻的那些边的向量也拿过来，甚至是把跟他相邻的那些顶点的向量也拿过来，以及全局向量，也就是说不仅使用本身的向量，还可以将别的跟本身相关的东西都拿过来一起做预测

对于来自于不同类别的属性，可以加在一起，合并在一起也可以。有一点像注意力机制（attention就是说将当前query的顶点和跟他相近的东西都拿过来，可以直接用图的信息将这些相近的向量拿过来，这样就完成了基于消息传递的图神经网络的工作）

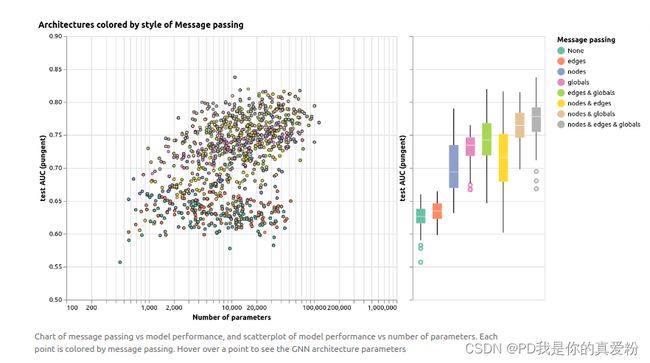
GNN实验部分

GNN的实验做的是一个分子图结构的预测问题， 就是通过分子图结构来判断该分子是否刺鼻；分子的组成是碳、氮、氧、氟的原子与单、双、三键等；

• embedding长度对结果的影响

• GNN层数对结果的影响

• 聚合方式对结果的影响

• 消息传递方式对结果的影响

超参数总结

总的来说，GNN对超参数还是比较敏感的，能调的超参数也很多

• GNN层数
• 属性的embedding长度
• 汇聚操作的方式
• 信息传递的方式

GNN相关的其他问题

其他类型的图

在图论中也介绍过，有多重图、超图、超节点、分层图，不同的图结构会对神经网络做信息汇聚的时候产生影响， 如下图所示， 左图是一个multi graph，顶点之间可以有多条边，比如左图中相邻顶点之间不同颜色的边表示不同种类的边(红色的表示无向边，绿色的表示有向边)， 右图表示图是分层的，其中一些顶点是一个子图

对图进行采样和batch

假设有很多层的时候，最后一层的顶点就算只看它的一近邻，最后顶点由于有很多层消息传递，所以它实际上是能看到一个很大的图，在图连通性足够的情况下，最后这个顶点有可能会看到整个图的信息

在计算梯度的时候，需要把整个forward中所有的中间变量存下来，如果最后一层的顶点想要看整个图的话，意味着在算梯度的时候需要把整个图的中间结果都存下来，就导致计算量大到无法承受，因此就需要对图进行采样

• 在图中每次采样一个小图出来，在这个小图上做信息的汇聚，这样算梯度的时候就只需要将小图上的中间结果记录下来就行了

• 第一幅图表示随机采样(黄色点)，然后将这些点最近的一近邻(红色点)找出
• 第二幅图表示随机游走采样： 从某一个顶点开始，然后随机在图中找一条边，然后沿着这条边走到下一个顶点
• 第三幅图表示上述两种方法合并：先随机游走，再取这些点的一近邻
• 第四幅图表示K步的宽度遍历

从性能上考虑，不希望对每一个顶点逐步逐步更新，这样每一步的计算量太小，不利于并行，希望是像别的神经网络一样，将小样本做成小批量，这样来对大的矩阵或者tensor做运算

• 这里存在一个问题：每一个顶点的邻居的个数是不一样的，如何将这些顶点的邻居通过合并变成一个规则的张量是一个具有挑战性的问题(也就是说本文没给出解决方案)

总结

• 图是一个非常强大的工具，基本上所有的数据都能够表示成图，但也存在问题：在图上进行优化非常困难，因为图是稀疏架构，每个结构都是动态结构，使得计算比较困难
• 图神经网络对超参数是非常敏感的
• 上述两个原因导致图神经网络的门槛比较高，在工业上的应用依然比较少

引用文章：

• A Gentle Introduction to Graph Neural Networks https://distill.pub/2021/gnn-intro/
• 零基础多图详解图神经网络（GNN/GCN）【论文精读】 https://www.bilibili.com/video/BV1iT4y1d7zP