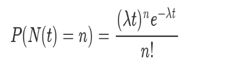人工智能-数学基础-数据科学必备分布

正态分布

import numpy as np
import scipy.stats as stats  #在scipy中把各种分布的函数拿到手
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML

%matplotlib inline
style.use('fivethirtyeight')   
plt.rcParams["figure.figsize"] = (14,7)
plt.figure(dpi=100)   #单位面积像素多少

#PDF  概率密度函数  默认参数μ=0 σ=1
plt.plot(np.linspace(-4,4,100),
        stats.norm.pdf(np.linspace(-4,4,100))/np.max(stats.norm.pdf(np.linspace(-3,3,100)))  #除以这个数是为了图形更高一点
        )
plt.fill_between(np.linspace(-4,4,100),    #如果只是一条线，太难看了。
                  stats.norm.pdf(np.linspace(-4,4,100),loc=2,scale=0.5)/np.max(stats.norm.pdf(np.linspace(-3,3,100))),
                 alpha=0.5,
                )

#CDF  累计概率密度函数
plt.plot(np.linspace(-4,4,100),
        stats.norm.cdf(np.linspace(-4,4,100)))

# 从特定正态分布中选取随机数
from scipy.stats import norm
print(norm.rvs(loc=10,scale=4,size=10),end="\n\n")

#[ 9.02505529  4.24482163  3.94200483  7.22089137  8.8781777   7.67380599 9.41988128 #10.39018509 10.23039513 10.26075038]

# 求概率密度函数的特定值
x = -1
y = 2
print("pdf(x)={}\npdf(y)={}".format(norm.pdf(x),norm.pdf(y)))  

#pdf(x)=0.24197072451914337   pdf(y)=0.05399096651318806


#求累计概率密度函数特定值
print("P(x<0.3) = {}".format(norm.cdf(0.3)))
print("P(-0.3

---

二项式分布

1. 每个试验都是独立的。
2. 在试验中只有两个可能的结果：成功或失败。
3. 总共进行了n次相同的试验。
4. 所有试验成功和失败的概率是相同的。 （试验是一样的，但不一定都是0.5）

• PMF( 概率质量函数 ): 是对 离散随机变量 的定义. 是 离散随机变量 在各个特定取值的概率。
• PDF ( 概率密度函数 ): 是对 连续性随机变量 的定义. 与PMF不同的是 PDF 在特定点上的值并不是该点的概率, 连续随机概率事件只能求一段区域内发生事件的概率, 通过对这段区间进行积分来求。

图像和正态的画法相似，就是把pdf换成pmf，norm换成binom

---

泊松分布

假定一个事件在一段时间内随机发生，且符合以下条件：

1. 将该时间段无限分隔成若干个小的时间段，在这个接近于零的小时间段里，该事件发生一次的概率与这个极小时间段的长度成正比。
2. 在每一个极小时间段内，该事件发生两次及以上的概率恒等于零。
3. 该事件在不同的小时间段里，发生与否相互独立。

医院的例子，如果我们把一天分成24个小时，或者24x60分钟，或者24x3600秒。时间分的越短，这个时间段里来病人的概率就越小（比如说医院在正午12点到正午12点又一毫秒之间来病人的概率是不是很接近于零？）。 条件一符合。另外如果我们把时间分的很细很细，是不是同时来两个病人（或者两个以上的病人）就是不可能的事件？即使两个病人同时来，也总有一个人先迈步子跨进医院大门吧。条件二也符合。倒是条件三的要求比较苛刻。应用到实际例子中就是说病人们来医院的概率必须是相互独立的，如果不是，则不能看作是poisson分布。

常见符合泊松分布的场景

• 某个地区在一天内报告的失窃的数量。
• 在一小时内抵达沙龙的客户人数。
• 书中每一页打印错误的数量。

公式

λ是事件发生的速率，t是时间间隔的长，X是该时间间隔内的事件数。其中，X称为泊松随机变量，X的概率分布称为泊松分布。令μ表示长度为t的间隔中的平均事件数。那么，µ = λ*t。

例如：已知平均每小时出生3个婴儿，接下来两个小时，一个婴儿都不出生的概率是？

上面就是泊松分布的公式。等号的左边，P 表示概率，N表示某种函数关系，t 表示时间，n 表示数量，1小时内出生3个婴儿的概率，就表示为 P(N(1) = 3) 。等号的右边，λ 表示事件的频率。

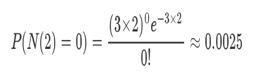接下来两个小时，一个婴儿都不出生的概率是0.25%，基本不可能发生。

泊松分布的图形大概形状：

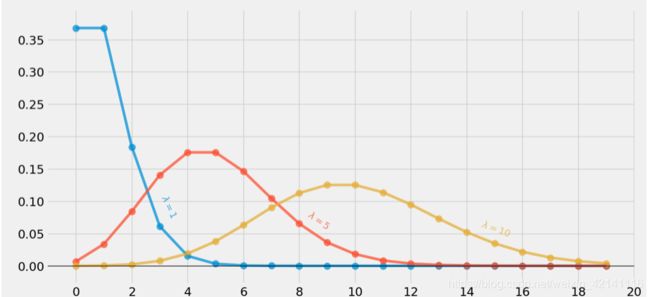
泊松分布改变λ

---

均匀分布

对于投骰子来说，结果是1到6。得到任何一个结果的概率是相等的，这就是均匀分布的基础。与伯努利分布不同，均匀分布的所有可能结果的n个数也是相等的。

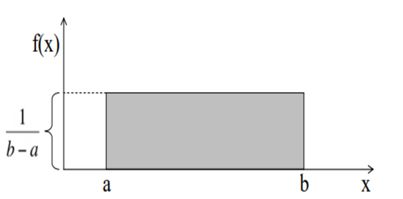
均匀分布的曲线：

---

卡方分布

通俗的说就是通过小数量的样本容量去预估总体容量的分布情况 

卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度

若n个相互独立的随机变量ξ₁，ξ₂，...,ξn ，均服从标准正态分布（也称独立同分布于标准正态分布），则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律称为卡方分布（chi-square distribution）

自由度：假设你现在手头有 3 个样本，。因为样本具有随机性，所以它们取值不定。但是假设出于某种原因，我们需要让样本均值固定，比如说， ， 那么这时真正取值自由，”有随机性“ 的样本只有 2 个。 试想，如果 ,那么每选取一组 的取值， 将不得不等于 对于第三个样本来说，这种 “不得不” 就可以理解为被剥夺了一个自由度。所以就这个例子而言，3 个样本最终"自由"的只有其中的 2 个。不失一般性， 个样本， 留出一个自由度给固定的均值，剩下的自由度即为 。

卡方检验的基本思想是根据样本数据推断总体的频次与期望频次是否有显著性差异

---

beta分布

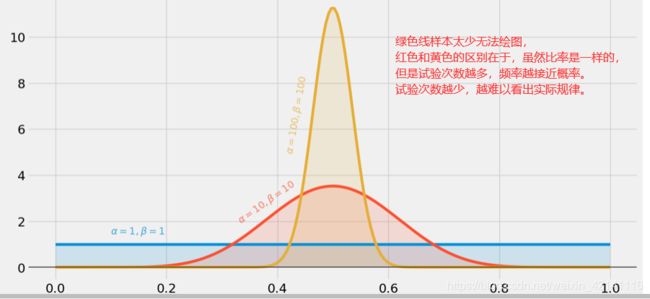
beta分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小

举一个简单的例子，熟悉棒球运动的都知道有一个指标就是棒球击球率(batting average)，就是用一个运动员击中的球数除以击球的总数，我们一般认为0.266是正常水平的击球率，而如果击球率高达0.3就被认为是非常优秀的。现在有一个棒球运动员，我们希望能够预测他在这一赛季中的棒球击球率是多少。你可能就会直接计算棒球击球率，用击中的数除以击球数，但是如果这个棒球运动员只打了一次，而且还命中了，那么他就击球率就是100%了，这显然是不合理的，因为根据棒球的历史信息，我们知道这个击球率应该是0.215到0.36之间才对啊。对于这个问题一个最好的方法就是用beta分布，这表示在我们没有看到这个运动员打球之前，我们就有了一个大概的范围。beta分布的定义域是(0,1)这就跟概率的范围是一样的。接下来我们将这些先验信息转换为beta分布的参数，我们知道一个击球率应该是平均0.27左右，而他的范围是0.21到0.35，那么根据这个信息，我们可以取α=81,β=219（击中了81次，未击中219次）