Fuzzy C-Means Clustering(模糊C均值)

别看了 有错的 我懒得改了

强推https://www.bilibili.com/video/BV18J411a7yY?t=591

看完你还不会那我也没办法了

\

算法原理

  模糊c-均值聚类算法 fuzzy c-means algorithm (FCMA)或称（FCM）。在众多模糊聚类算法中，模糊C-均值（FCM）算法应用最广泛且较成功，它通过优化目标函数得到每个样本点对所有类中心的隶属度，从而决定样本点的类属以达到自动对样本数据进行分类的目的。
  先来讲讲这个算法的名字噢，什么叫Fuzzy，什么叫模糊呢，在经典的集合理论，一个元素是否属于集合，只有真或者假两种情况，也可以说只有0和1两种情况，0为假1为真。比如我们想要定义一个集合表示“年轻人”，那么我们需要设置一个阈值，当一个人的年龄小于这阈值的时候，就认为这个人属于这个集合，反之则不属于。假如用A表示年轻人这个集合，以20岁为阈值。则这个集合的隶属度函数可以表示如下：
$${\mu }_A(z)=\{\begin{array}{l}1,z<20\\ 0,z\ge 20\end{array}$$
上面的公式可以用下面左图表示：

  使用经典的集合理论，我们会面临着一些实际的问题，比如当一个人的年龄是20岁零1秒的时候，这个人就不再是年轻人了，这种粗暴的分类方式，在实际中并不实用。因此我们需要有过渡的函数来描述这个情况。上图中右边的图提供了一种解决方法，图中的斜线表示年龄的过渡。
于是就可以定义三个隶属度函数来确定年龄与三个模糊子集的关系：
$${\mu }_A(z)=\{\begin{array}{l}1,z\le 20\\ \frac{30-z}{10},20<z<30\\ 0,z\ge 30\end{array}$$
  OK，模糊的概念大概懂了，那么C-Means的C又是什么东西呢，额这个，好像没有什么含义，就像K-Means的k一样，只是代表聚类的个数，可能是cluster的c?又可能是模糊控制器(Fuzzy Controller)里的c。但是这个无关紧要，懂得模糊的概念就好了。

  然后我们来正式说一下模糊c-均值是什么。模糊c-均值是一种允许一个数据属于一个或多个簇的方法，它不同于K-Means一个数据只能属于一个簇，它自发明以来广泛应用于模式识别中。
  那么这种算法它的优化目标、目标函数是什么呢?看下面的公式：
$$\begin{gathered} min{J}_m=\sum _{i=1}^N\sum _{j=1}^C{\mu }_{ij}^m||x_i-v_j|{|}^2,1<m<\infty \\ s.t.\sum _{j=1}^C{\mu }_{ij}=1\text{\hspace{1em}(1)} \end{gathered}$$
符号定义：
$N:$ 是样本总个数
$C:$ 簇心数目，就是一开始输入的参数，你想这N个数据分成3份就将C置为3，5份就置为5，懂吧
$\mu :$ 一个$N\times C$的矩阵，其中${\mu }_{ij}$是$x_i$属于类别$j$的隶属度
$v_j:$ 第$j$个类别的中心
$m:$ 跟$C$一样是自己设置的参数，不同的$m$会有不同的聚类效果，需要根据不同的数据集进行调节

这个公式呢就是说每一个数据$x_i$到每一个聚类中心$v_j$距离的二范式再乘上$x_i$属于类别$j$的隶属度的$m$次方，要最小化它们的总和，直观一点就是希望每一个数据尽可能与它们所属的聚类中心接近。

  那么就开始求如何使这个函数最小化了，(众所周知)，求最小嘛，基本操作将它对某个变量求偏导，令偏导结果为零即可，因为有一个等式约束，我们先引入拉格朗日乘子$\lambda$，于是原式可以写成：

$$minJ=\sum _{i=1}^N\sum _{j=1}^C{\mu }_{ij}^m||x_i-v_j|{|}^2-\lambda (\sum _{j=1}^C{\mu }_{ij}-1)\text{\hspace{1em}(2)}$$
然后对$\lambda$求偏导并令其为零，得：
$$\frac{\partial J}{\partial \lambda }=\sum _{j=1}^C{\mu }_{ij}-1=0\text{\hspace{1em}(3)}$$
再对${\mu }_{ij}$求偏导并令其为零，得：
$$\frac{\partial J}{\partial {\mu }_{ij}}=m\cdot {\mu }_{ij}^{m-1}||x_i-v_j|{|}^2-\lambda =0\text{\hspace{1em}(4)}$$
由(4)可得
$${\mu }_{ij}={\left(\frac{\lambda }{m||x_i-v_j|{|}^2}\right)}^{\frac{1}{m-1}}\text{\hspace{1em}(5)}$$
将(5)代入(3)得：
$$\begin{array}{rl}\sum _{j=1}^C{\left(\frac{\lambda }{m||x_i-v_j|{|}^2}\right)}^{\frac{1}{m-1}}-1& =0\\ \sum _{j=1}^C{\left(\frac{\lambda }{m}\right)}^{\frac{1}{m-1}}{\left(\frac{1}{||x_i-v_j|{|}^2}\right)}^{\frac{1}{m-1}}-1& =0\\ {\left(\frac{\lambda }{m}\right)}^{\frac{1}{m-1}}\sum _{j=1}^C{\left(\frac{1}{||x_i-v_j|{|}^2}\right)}^{\frac{1}{m-1}}-1& =0\end{array}$$
于是我们就可以得到：
$${\left(\frac{\lambda }{m}\right)}^{\frac{1}{m-1}}=\frac{1}{{\sum }_{j=1}^C{\left(\frac{1}{||x_i-v_j|{|}^2}\right)}^{\frac{1}{m-1}}}\text{\hspace{1em}(6)}$$
将(6)再代入(4)得：
$${\mu }_{ij}=\frac{1}{{\sum }_{k=1}^C{\left(\frac{1}{||x_i-v_k|{|}^2}\right)}^{\frac{1}{m-1}}}{\left(\frac{1}{||x_i-v_j|{|}^2}\right)}^{\frac{1}{m-1}}=\frac{1}{{\sum }_{k=1}^C{\left(\frac{||x_i-v_j|{|}^2}{||x_i-v_k|{|}^2}\right)}^{\frac{1}{m-1}}}\text{\hspace{1em}(7)}$$

再对$v_i$求偏导并令其为零，得：
$$\frac{\partial J}{\partial v_i}=-2\sum _{i=1}^N{\mu }_{ij}^m(x_i-v_j)\text{\hspace{1em}(8)}$$
$$v_j=\frac{{\sum }_{i=1}^N{\mu }_{ij}^m{x}_i}{{\sum }_{i=1}^N{\mu }_{ij}^m}\text{\hspace{1em}(9)}$$
式(9)即为聚类中心$v_j$的更新公式。

总结一下模糊C均值的更新公式如下：
$${\mu }_{ij}=\frac{1}{{\sum }_{k=1}^C{\left(\frac{||x_i-v_j|{|}^2}{||x_i-v_k|{|}^2}\right)}^{\frac{1}{m-1}}}{v}_j=\frac{{\sum }_{i=1}^N{\mu }_{ij}^m{x}_i}{{\sum }_{i=1}^N{\mu }_{ij}^m}$$

算法步骤

---

1. 确定类别数C，参数m，和迭代停止误差$\epsilon$以及最大迭代次数T
2. 初始化聚类中心$V=\{v_1,v_2,...,v_C\}$
3. For t=1 to T:
     Calculate $U_t$ with $V_{t-1}$ and (7)
     Calculate $V_t$ with $U_t$ and (9)
     If $E_t=||V_t-V_{t-1}|{|}_{err}\le \epsilon$
     Stop and put $(U_f,V_f)=(U_t,V_t)$; Else
   Next t

---

举个例子

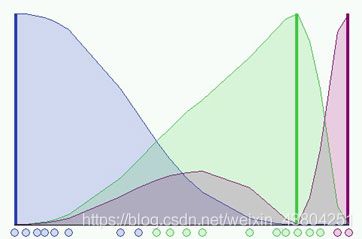
我们考虑FCM在一维下应用的情况。 使用二十个数据和三个聚类来初始化算法并计算U矩阵。 下图显示了每个基准面和每个聚类的成员隶属度。 根据隶属函数，数据的颜色是最近的群集的颜色。

在上图所示的仿真中，我们使用了模糊系数 $m=2$，其中模糊分布取决于簇的特定位置。 因为尚未执行任何步骤，所以无法很好地识别群集。 现在可以运行算法，直到验证停止条件为止。 下图显示了在第8步达到的最终条件，其中 $m=2$ 和 $\epsilon =0.3$：

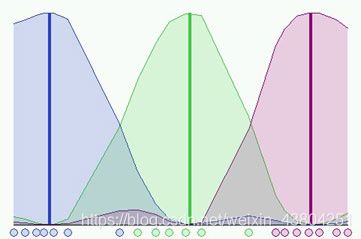
不同的初始化会导致算法的不同演化，它们可以收敛到相同的结果，但是迭代步骤的数量就不一样了。

python实现FCM对iris数据集进行聚类

import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
import scipy.io as scio

C = 3
m = 2
# T = 5000
# EPS = 0.0000001
colors = ['r', 'b', 'g']

def norm2(x):
    x = np.mat(x)
    return np.dot(x.reshape(1, -1), x.reshape(-1, 1))


def cal(x_i, c_j, c_k):
    x_i = np.mat(x_i).reshape(1, -1)
    c_j = np.mat(c_j).reshape(1, -1)
    c_k = np.mat(c_k).reshape(1, -1)
    return float(np.power(norm2(x_i-c_j)/norm2(x_i-c_k), 2.0/(m-1)))


def fuzzy_c_means(data, m, C, EPS, T):
    data = np.mat(data)
    n, p = data.shape
    V = [np.random.random([1, p]) for _ in range(C)]
    U = [[0 for i in range(C)] for j in range(n)]
    for i in range(n):
        for j in range(C):
            down = 0
            for k in range(C):
                down += cal(data[i], V[j], V[k])
            U[i][j] = 1.0/down
    for _ in range(T):
        for j in range(C):
            down = 0
            V[j] = np.zeros([1, p])
            for i in range(n):
                u_i_j_m = pow(U[i][j], m)
                V[j] += data[i]*u_i_j_m
                down += u_i_j_m
            V[j] /= down

        upgrade = 0
        for i in range(n):
            for j in range(C):
                down = 0
                for k in range(C):
                    down += cal(data[i], V[j], V[k])
                tmp = 1.0 / down
                upgrade += abs(U[i][j]-tmp)
                U[i][j] = tmp

        if upgrade < EPS:
            break
    for i in range(n):
        idx = np.argmax(U[i])
        plt.scatter(float(data[i][:, 0]), float(data[i][:, 1]), c=colors[idx])
    plt.show()


if __name__ == '__main__':
    a = datasets.load_iris()
    data = a['data']
    pca = PCA(n_components=2)
    data = pca.fit_transform(data)
    fuzzy_c_means(data=data, m=2, C=C, EPS=1e-7, T=5000)

原数据通过PCA降到二维空间中的分布情况如下图所示

通过FCM进行聚类后的结果如下图所示

参考博客

http://home.deib.polimi.it/matteucc/Clustering/tutorial_html/cmeans.html
https://blog.csdn.net/einsdrw/article/details/37930331