scipy.optimize.curve_fit
使用scipy.optimize.curve_fit对数据进行幂函数、指数拟合。
1.函数各参数说明
scipy.optimize.curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False, check_finite=True, bounds=(- inf, inf), method=None, jac=None, *kwargs)
(1)f:模型函数;即需要进行拟合的函数,含有自变量X和其他变量如A,B,C等。
如想拟合函数为:$$y = a(x-b)^c
def PowerFunction(x, A, B,C):
y = A*(x-B)**C
return y
(2)xdata:观测数据自变量(数组),长度为M;
(3)ydata:观测数据因变量(数组),长度为M;
(4)p0:对参数的初始猜测(长度N)。如果为None,那么初始值将全部为1。确定初始值,可以减少计算量。
(5)method:用于优化的方法,对于无约束的问题默认为lm,如果提供了边界则默认为trf。
(6)函数返回值:
popt :返回残差最小时参数的值;
pcov:popt的估计协方差。
2.使用函数
代码来源:https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
def func(x, a, b, c):
return a * np.exp(-b * x) + c
#Define the data to be fit with some noise
xdata = np.linspace(0, 4, 50)
y = func(xdata, 2.5, 1.3, 0.5)
rng = np.random.default_rng()
y_noise = 0.2 * rng.normal(size=xdata.size)
ydata = y + y_noise
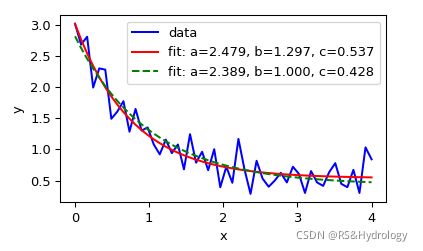
plt.plot(xdata, ydata, 'b-', label='data')
#Fit for the parameters a, b, c of the function func
popt, pcov = curve_fit(func, xdata, ydata)
plt.plot(xdata, func(xdata, *popt), 'r-',
label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
#Constrain the optimization to the region of 0 <= a <= 3, 0 <= b <= 1 and 0 <= c <= 0.5
popt, pcov = curve_fit(func, xdata, ydata, bounds=(0, [3., 1., 0.5]))
plt.plot(xdata, func(xdata, *popt), 'g--',
label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
#R²
calc_ydata = [func(i, popt[0], popt[1],popt[2]) for i in xdata]
res_ydata = np.array(ydata) - np.array(calc_ydata)
ss_res = np.sum(res_ydata**2)
ss_tot = np.sum((ydata - np.mean(ydata))**2)
r_squared = 1 - (ss_res / ss_tot)
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()