【研究生工作周报】(DDPM)
文章目录
- 前言
- 一、Loss计算
-
- 计算 x t x_t xt:
- 计算 α ˉ t \bar{\alpha}_{t} αˉt
- 二、训练目标和采样目标
-
- 正向过程
- 逆向过程
- 二、Unet结构
- 总结
-
- Diffusion Models和GANs结合
- 代码地址汇总
前言
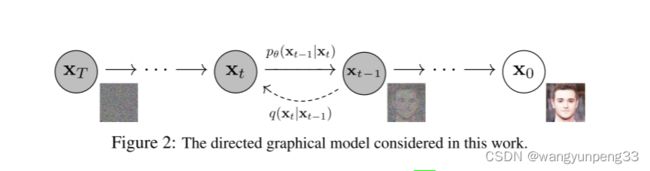
扩散模型包括两个过程:
前向过程(forward process)和反向过程(reverse process),其中前向过程又称为扩散过程(diffusion process),如下图所示。无论是前向过程还是反向过程都是一个参数化的马尔可夫链(Markov chain),其中反向过程可以用来生成数据,这里我们将通过变分推断来进行建模和求解
一、Loss计算
论文中的loss公式:
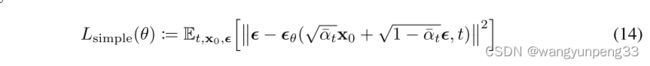
计算的是纯噪声 ϵ \boldsymbol{\epsilon} ϵ 和 ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ , t ) \boldsymbol{\epsilon}_{\theta}\left(\sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}, t\right) ϵθ(αˉtx0+1−αˉtϵ,t) 之间的均方差:
noise = torch.randn_like(x_0)#其中noise的size是input_data一样的
loss = F.mse_loss(self.model(x_t, t), noise, reduction='none')
计算 x t x_t xt:
x t = α ˉ t x 0 + 1 − α ˉ t ϵ x_t = \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon} xt=αˉtx0+1−αˉtϵ
其中时刻信息 t 是通过 α ˉ t \bar{\alpha}_{t} αˉt 表现的。
extract函数的作用是选取特定下标t的信息并转换成特定维度。
具体实现:
def extract(v, t, x_shape):
"""
Extract some coefficients at specified timesteps, then reshape to
[batch_size, 1, 1, 1, 1, ...] for broadcasting purposes.
"""
out = torch.gather(v, index=t, dim=0).float()
return out.view([t.shape[0]] + [1] * (len(x_shape) - 1))
x_t = (
extract(self.sqrt_alphas_bar, t, x_0.shape) * x_0 +
extract(self.sqrt_one_minus_alphas_bar, t, x_0.shape) * noise)
计算 α ˉ t \bar{\alpha}_{t} αˉt
先根据 β 1 \beta_1 β1和 β T \beta_T βT计算所有的 β t \beta_t βt
DDPM原始的论文设置的是线性增长,后面的论文有设置指数增长等其他方式。
self.register_buffer(
'betas', torch.linspace(beta_1, beta_T, T).double())
再根据 β t \beta_t βt计算 α t \alpha_t αt
α t = 1 − β t \alpha_t = 1 - \beta_t αt=1−βt
alphas = 1. - self.betas
累乘得到 α t ˉ \bar{\alpha_t} αtˉ
alphas_bar = torch.cumprod(alphas, dim=0)
最后将这些写入buffer
self.register_buffer(
'sqrt_alphas_bar', torch.sqrt(alphas_bar))
self.register_buffer(
'sqrt_one_minus_alphas_bar', torch.sqrt(1. - alphas_bar))
将 x t x_t xt,t 输入到神经网络得到预测噪声 ϵ θ \boldsymbol{\epsilon}_{\theta} ϵθ ,再根据公式不断采样得到 x 0 x_0 x0
self.register_buffer(
'posterior_log_var_clipped',
torch.log(
torch.cat([self.posterior_var[1:2], self.posterior_var[1:]])))
self.register_buffer(
'posterior_mean_coef1',
torch.sqrt(alphas_bar_prev) * self.betas / (1. - alphas_bar))
self.register_buffer(
'posterior_mean_coef2',
torch.sqrt(alphas) * (1. - alphas_bar_prev) / (1. - alphas_bar))
def predict_xstart_from_xprev(self, x_t, t, xprev):
assert x_t.shape == xprev.shape
return ( # (xprev - coef2*x_t) / coef1
extract(
1. / self.posterior_mean_coef1, t, x_t.shape) * xprev -
extract(
self.posterior_mean_coef2 / self.posterior_mean_coef1, t,
x_t.shape) * x_t
二、训练目标和采样目标
正向过程
正向过程即p过程,逆向过程即q过程、采样过程。
正向过程不涉及参数分布的计算和预测,可以理解为一个单纯add noise的过程。
class GaussianDiffusionTrainer(nn.Module):
def __init__(self, model, beta_1, beta_T, T):
super().__init__()
self.model = model
self.T = T
self.register_buffer(
'betas', torch.linspace(beta_1, beta_T, T).double())
alphas = 1. - self.betas
alphas_bar = torch.cumprod(alphas, dim=0)
# calculations for diffusion q(x_t | x_{t-1}) and others
self.register_buffer(
'sqrt_alphas_bar', torch.sqrt(alphas_bar))
self.register_buffer(
'sqrt_one_minus_alphas_bar', torch.sqrt(1. - alphas_bar))
def forward(self, x_0):
"""
Algorithm 1.
"""
t = torch.randint(self.T, size=(x_0.shape[0], ), device=x_0.device)
noise = torch.randn_like(x_0)
x_t = (
extract(self.sqrt_alphas_bar, t, x_0.shape) * x_0 +
extract(self.sqrt_one_minus_alphas_bar, t, x_0.shape) * noise)
loss = F.mse_loss(self.model(x_t, t), noise, reduction='none')
return loss
逆向过程
x t x_t xt 的分布符合高斯分布,这是通过均值和方差进行计算的:
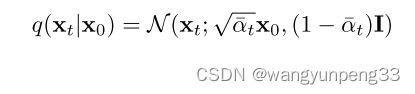
计算 σ t Z \sigma_{t} \mathbf{Z} σtZ 使用:
torch.exp(0.5 * log_var) * noise
重点是计算这里的均值:
我们输入 x t x_t xt , 得到 x t − 1 x_{t-1} xt−1

Alg1+Alg2 完整代码:
class GaussianDiffusionSampler(nn.Module):
def __init__(self, model, beta_1, beta_T, T, img_size=32,
mean_type='eps', var_type='fixedlarge'):
assert mean_type in ['xprev' 'xstart', 'epsilon']
assert var_type in ['fixedlarge', 'fixedsmall']
super().__init__()
self.model = model
self.T = T
self.img_size = img_size
self.mean_type = mean_type
self.var_type = var_type
self.register_buffer(
'betas', torch.linspace(beta_1, beta_T, T).double())
alphas = 1. - self.betas
alphas_bar = torch.cumprod(alphas, dim=0)
alphas_bar_prev = F.pad(alphas_bar, [1, 0], value=1)[:T]
# calculations for diffusion q(x_t | x_{t-1}) and others
self.register_buffer(
'sqrt_recip_alphas_bar', torch.sqrt(1. / alphas_bar))
self.register_buffer(
'sqrt_recipm1_alphas_bar', torch.sqrt(1. / alphas_bar - 1))
# calculations for posterior q(x_{t-1} | x_t, x_0)
self.register_buffer(
'posterior_var',
self.betas * (1. - alphas_bar_prev) / (1. - alphas_bar))
# below: log calculation clipped because the posterior variance is 0 at
# the beginning of the diffusion chain
self.register_buffer(
'posterior_log_var_clipped',
torch.log(
torch.cat([self.posterior_var[1:2], self.posterior_var[1:]])))
self.register_buffer(
'posterior_mean_coef1',
torch.sqrt(alphas_bar_prev) * self.betas / (1. - alphas_bar))
self.register_buffer(
'posterior_mean_coef2',
torch.sqrt(alphas) * (1. - alphas_bar_prev) / (1. - alphas_bar))
def q_mean_variance(self, x_0, x_t, t):
"""
Compute the mean and variance of the diffusion posterior
q(x_{t-1} | x_t, x_0)
"""
assert x_0.shape == x_t.shape
posterior_mean = (
extract(self.posterior_mean_coef1, t, x_t.shape) * x_0 +
extract(self.posterior_mean_coef2, t, x_t.shape) * x_t
)
posterior_log_var_clipped = extract(
self.posterior_log_var_clipped, t, x_t.shape)
return posterior_mean, posterior_log_var_clipped
def predict_xstart_from_eps(self, x_t, t, eps):
assert x_t.shape == eps.shape
return (
extract(self.sqrt_recip_alphas_bar, t, x_t.shape) * x_t -
extract(self.sqrt_recipm1_alphas_bar, t, x_t.shape) * eps
)
def predict_xstart_from_xprev(self, x_t, t, xprev):
assert x_t.shape == xprev.shape
return ( # (xprev - coef2*x_t) / coef1
extract(
1. / self.posterior_mean_coef1, t, x_t.shape) * xprev -
extract(
self.posterior_mean_coef2 / self.posterior_mean_coef1, t,
x_t.shape) * x_t
)
def p_mean_variance(self, x_t, t):
# below: only log_variance is used in the KL computations
model_log_var = {
# for fixedlarge, we set the initial (log-)variance like so to
# get a better decoder log likelihood
'fixedlarge': torch.log(torch.cat([self.posterior_var[1:2],
self.betas[1:]])),
'fixedsmall': self.posterior_log_var_clipped,
}[self.var_type]
model_log_var = extract(model_log_var, t, x_t.shape)
# Mean parameterization
if self.mean_type == 'xprev': # the model predicts x_{t-1}
x_prev = self.model(x_t, t)
x_0 = self.predict_xstart_from_xprev(x_t, t, xprev=x_prev)
model_mean = x_prev
elif self.mean_type == 'xstart': # the model predicts x_0
x_0 = self.model(x_t, t)
model_mean, _ = self.q_mean_variance(x_0, x_t, t)
elif self.mean_type == 'epsilon': # the model predicts epsilon
eps = self.model(x_t, t)
x_0 = self.predict_xstart_from_eps(x_t, t, eps=eps)
model_mean, _ = self.q_mean_variance(x_0, x_t, t)
else:
raise NotImplementedError(self.mean_type)
x_0 = torch.clip(x_0, -1., 1.)
return model_mean, model_log_var
def forward(self, x_T):
"""
Algorithm 2.
"""
x_t = x_T
for time_step in reversed(range(self.T)):
t = x_t.new_ones([x_T.shape[0], ], dtype=torch.long) * time_step
mean, log_var = self.p_mean_variance(x_t=x_t, t=t)
# no noise when t == 0
if time_step > 0:
noise = torch.randn_like(x_t)
else:
noise = 0
x_t = mean + torch.exp(0.5 * log_var) * noise
x_0 = x_t
return torch.clip(x_0, -1, 1)
二、Unet结构
- Unet的生成能力在GANs中早已被证明
- 在之前Unet结构的基础上,加入了attention和PE,形成了DDPM特有的Unet结构
Positional Embedding融入共享参数信息。positional embedding是transformer中一个重要的组成部分。因为在transformer中不包含RNN和CNN,为了让模型利用序列的顺序,必须注入一些关于序列中记号的相对或绝对位置的信息。
##DDPM中的位置编码
self.positional_embedding = nn.Parameter(th.randn(embed_dim, spacial_dim ** 2 + 1) / embed_dim ** 0.5)
x = x + self.positional_embedding[None, :, :].to(x.dtype) # NC(HW+1)
为此添加位置编码在编码器和解码器堆栈的底部。位置编码与嵌入具有相同的维数模型,因此可以将两者相加。位置编码可以是可学习的,也可以是固定的。
DDPM特有的Unet结构
import math
import torch
from torch import nn
from torch.nn import init
from torch.nn import functional as F
class Swish(nn.Module):
def forward(self, x):
return x * torch.sigmoid(x)
class TimeEmbedding(nn.Module):
def __init__(self, T, d_model, dim):
assert d_model % 2 == 0
super().__init__()
emb = torch.arange(0, d_model, step=2) / d_model * math.log(10000)
emb = torch.exp(-emb)
pos = torch.arange(T).float()
emb = pos[:, None] * emb[None, :]
assert list(emb.shape) == [T, d_model // 2]
emb = torch.stack([torch.sin(emb), torch.cos(emb)], dim=-1)
assert list(emb.shape) == [T, d_model // 2, 2]
emb = emb.view(T, d_model)
self.timembedding = nn.Sequential(
nn.Embedding.from_pretrained(emb),
nn.Linear(d_model, dim),
Swish(),
nn.Linear(dim, dim),
)
self.initialize()
def initialize(self):
for module in self.modules():
if isinstance(module, nn.Linear):
init.xavier_uniform_(module.weight)
init.zeros_(module.bias)
def forward(self, t):
emb = self.timembedding(t)
return emb
class DownSample(nn.Module):
def __init__(self, in_ch):
super().__init__()
self.main = nn.Conv2d(in_ch, in_ch, 3, stride=2, padding=1)
self.initialize()
def initialize(self):
init.xavier_uniform_(self.main.weight)
init.zeros_(self.main.bias)
def forward(self, x, temb):
x = self.main(x)
return x
class UpSample(nn.Module):
def __init__(self, in_ch):
super().__init__()
self.main = nn.Conv2d(in_ch, in_ch, 3, stride=1, padding=1)
self.initialize()
def initialize(self):
init.xavier_uniform_(self.main.weight)
init.zeros_(self.main.bias)
def forward(self, x, temb):
_, _, H, W = x.shape
x = F.interpolate(
x, scale_factor=2, mode='nearest')
x = self.main(x)
return x
class AttnBlock(nn.Module):
def __init__(self, in_ch):
super().__init__()
self.group_norm = nn.GroupNorm(32, in_ch)
self.proj_q = nn.Conv2d(in_ch, in_ch, 1, stride=1, padding=0)
self.proj_k = nn.Conv2d(in_ch, in_ch, 1, stride=1, padding=0)
self.proj_v = nn.Conv2d(in_ch, in_ch, 1, stride=1, padding=0)
self.proj = nn.Conv2d(in_ch, in_ch, 1, stride=1, padding=0)
self.initialize()
def initialize(self):
for module in [self.proj_q, self.proj_k, self.proj_v, self.proj]:
init.xavier_uniform_(module.weight)
init.zeros_(module.bias)
init.xavier_uniform_(self.proj.weight, gain=1e-5)
def forward(self, x):
B, C, H, W = x.shape
h = self.group_norm(x)
q = self.proj_q(h)
k = self.proj_k(h)
v = self.proj_v(h)
q = q.permute(0, 2, 3, 1).view(B, H * W, C)
k = k.view(B, C, H * W)
w = torch.bmm(q, k) * (int(C) ** (-0.5))
assert list(w.shape) == [B, H * W, H * W]
w = F.softmax(w, dim=-1)
v = v.permute(0, 2, 3, 1).view(B, H * W, C)
h = torch.bmm(w, v)
assert list(h.shape) == [B, H * W, C]
h = h.view(B, H, W, C).permute(0, 3, 1, 2)
h = self.proj(h)
return x + h
class ResBlock(nn.Module):
def __init__(self, in_ch, out_ch, tdim, dropout, attn=False):
super().__init__()
self.block1 = nn.Sequential(
nn.GroupNorm(32, in_ch),
Swish(),
nn.Conv2d(in_ch, out_ch, 3, stride=1, padding=1),
)
self.temb_proj = nn.Sequential(
Swish(),
nn.Linear(tdim, out_ch),
)
self.block2 = nn.Sequential(
nn.GroupNorm(32, out_ch),
Swish(),
nn.Dropout(dropout),
nn.Conv2d(out_ch, out_ch, 3, stride=1, padding=1),
)
if in_ch != out_ch:
self.shortcut = nn.Conv2d(in_ch, out_ch, 1, stride=1, padding=0)
else:
self.shortcut = nn.Identity()
if attn:
self.attn = AttnBlock(out_ch)
else:
self.attn = nn.Identity()
self.initialize()
def initialize(self):
for module in self.modules():
if isinstance(module, (nn.Conv2d, nn.Linear)):
init.xavier_uniform_(module.weight)
init.zeros_(module.bias)
init.xavier_uniform_(self.block2[-1].weight, gain=1e-5)
def forward(self, x, temb):
h = self.block1(x)
h += self.temb_proj(temb)[:, :, None, None]
h = self.block2(h)
h = h + self.shortcut(x)
h = self.attn(h)
return h
class UNet(nn.Module):
def __init__(self, T, ch, ch_mult, attn, num_res_blocks, dropout):
super().__init__()
assert all([i < len(ch_mult) for i in attn]), 'attn index out of bound'
tdim = ch * 4
self.time_embedding = TimeEmbedding(T, ch, tdim)
self.head = nn.Conv2d(3, ch, kernel_size=3, stride=1, padding=1)
self.downblocks = nn.ModuleList()
chs = [ch] # record output channel when dowmsample for upsample
now_ch = ch
for i, mult in enumerate(ch_mult):
out_ch = ch * mult
for _ in range(num_res_blocks):
self.downblocks.append(ResBlock(
in_ch=now_ch, out_ch=out_ch, tdim=tdim,
dropout=dropout, attn=(i in attn)))
now_ch = out_ch
chs.append(now_ch)
if i != len(ch_mult) - 1:
self.downblocks.append(DownSample(now_ch))
chs.append(now_ch)
self.middleblocks = nn.ModuleList([
ResBlock(now_ch, now_ch, tdim, dropout, attn=True),
ResBlock(now_ch, now_ch, tdim, dropout, attn=False),
])
self.upblocks = nn.ModuleList()
for i, mult in reversed(list(enumerate(ch_mult))):
out_ch = ch * mult
for _ in range(num_res_blocks + 1):
self.upblocks.append(ResBlock(
in_ch=chs.pop() + now_ch, out_ch=out_ch, tdim=tdim,
dropout=dropout, attn=(i in attn)))
now_ch = out_ch
if i != 0:
self.upblocks.append(UpSample(now_ch))
assert len(chs) == 0
self.tail = nn.Sequential(
nn.GroupNorm(32, now_ch),
Swish(),
nn.Conv2d(now_ch, 3, 3, stride=1, padding=1)
)
self.initialize()
def initialize(self):
init.xavier_uniform_(self.head.weight)
init.zeros_(self.head.bias)
init.xavier_uniform_(self.tail[-1].weight, gain=1e-5)
init.zeros_(self.tail[-1].bias)
def forward(self, x, t):
# Timestep embedding
temb = self.time_embedding(t)
# Downsampling
h = self.head(x)
hs = [h]
for layer in self.downblocks:
h = layer(h, temb)
hs.append(h)
# Middle
for layer in self.middleblocks:
h = layer(h, temb)
# Upsampling
for layer in self.upblocks:
if isinstance(layer, ResBlock):
h = torch.cat([h, hs.pop()], dim=1)
h = layer(h, temb)
h = self.tail(h)
assert len(hs) == 0
return h
if __name__ == '__main__':
batch_size = 8
model = UNet(
T=1000, ch=128, ch_mult=[1, 2, 2, 2], attn=[1],
num_res_blocks=2, dropout=0.1)
x = torch.randn(batch_size, 3, 32, 32)
t = torch.randint(1000, (batch_size, ))
y = model(x, t)
Unet结构:
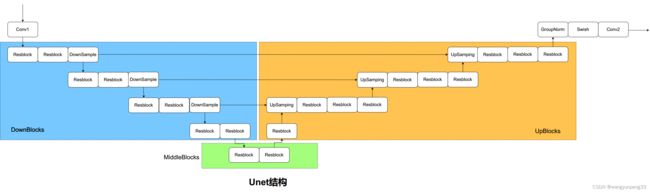
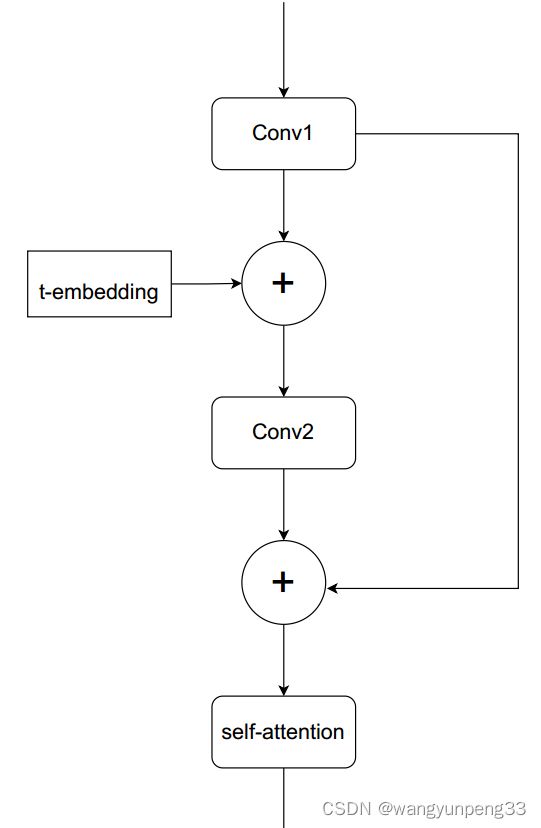
ResBlock基础模块:
引入时间编码 t ,self-attention机制
总结
DDPM有一个致命的问题,就是运算量过大,采样时间过长,如何加速这个采样时间?后续DDIM针对这个问题提出非马尔科夫链的生成模型。
在DDPMS中,生成过程被定义为特定马尔可夫扩散过程的反向过程。 我们通过一类非马尔可夫扩散过程将DDPMS推广到具有相同训练目标的非马尔可夫扩散过程。 这些非马尔可夫过程可以对应于确定性的生成过程,从而产生更快地产生高质量样本的隐式模型。
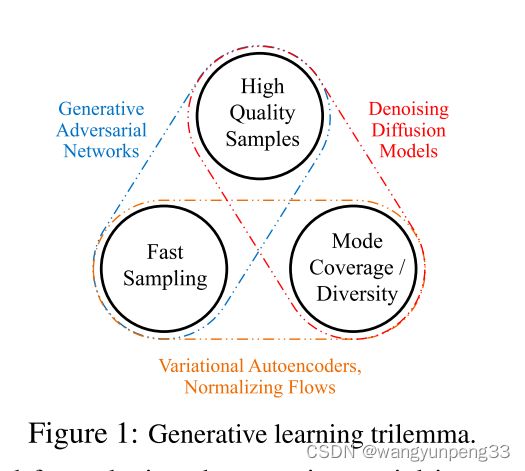
Diffusion Models和GANs结合
DENOISING DIFFUSION GANS 论文地址
在本文中,我们认为这些模型中的慢采样从根本上归因于去噪步骤中的高斯假设,这种假设只适用于小步长。 为了实现大步长的去噪,从而减少去噪的总步数,我们提出了用复多峰分布来建模去噪分布。 我们引入了去噪扩散生成对抗网络(去噪扩散网络),该网络使用多模态条件GAN对每个去噪步骤进行建模。
代码地址汇总
diffusion models beats gans onimage syntheisis:https://github.com/openai/guided-diffusion
improved denoise diffusion probabilistic models:https://github.com/openai/improved-diffusion
DDPM MNIST:https://github.com/abarankab/DDPM
DDPM官方代码(TPU版本):https://github.com/hojonathanho/diffusion
pytorch cifar10:https://github.com/w86763777/pytorch-ddpm
DDPM官方版本pytorch实现:GitHub - lucidrains/denoising-diffusion-pytorch: Implementation of Denoising Diffusion Probabilistic Model in Pytorch