语义分割重要方法和机制1（上采样）

目录

一、上采样方式

1.1 反卷积(转置卷积)                                                                               

1.1.1反卷积介绍

1.1.2反卷积图例

 1.1.3代码

1.2 双线性插值上采样

1.2.1方法介绍

1.2.2双线性插值法

1.2.3代码

1.3反池化上采样

1.3.1反池化介绍

1.3.2优点

1.3.3代码

二.参考资料

一、上采样方式

1.1 反卷积(转置卷积)                                                                               

1.1.1反卷积介绍

        转置卷积是用来增大输入的大小，以增加分辨率而细化特征图。其类似卷积的逆向过程。其公式为： out = (Input - 1) * stride + kernel - 2*padding （其中out对应输出,input对应输入,stride对应步长,kernel对应反卷积核,padding是在空白位置补0）

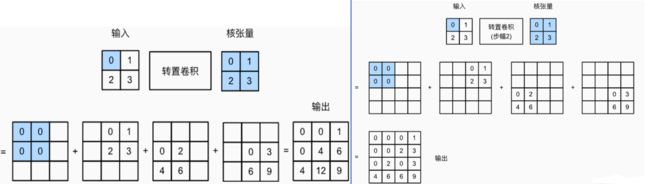
1.1.2反卷积图例

        下图对应了滑动步长（Stride）1和2的情况。

 1.1.3代码

        代码1:（步长为1）转置卷积过程

import torch
def trans_conv(X, K):                #定义转置卷积函数 参数为（X,K）
    h, w = K.shape                             #变量为h,w  K.shape值赋
    Y = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1)) #zeros是返回形状为size,类型为torch.dtype，里面的每一个值都是0的tensor shape[0.1]是行和列
    for i in range(X.shape[0]):            #对行进行遍历
        for j in range(X.shape[1]):              #对列进行遍历
            Y[i:i+h, j:j+w] += X[i, j] * K
    return Y
X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])       #X为输入 
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])       #K为核张量
print(trans_conv(X,K))

        代码2：（步长为2）的转置卷积过程

import torch
def trans_conv(X, K, stride=2):
    h, w = K.shape
    Y = torch.zeros(((X.shape[0] - 1) * stride + h, (X.shape[1] - 1) * stride + w))
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            Y[i * stride:i * stride +h, j * stride:j * stride +w] += X[i, j] * K
    return Y
X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
print(trans_conv(X,K))

1.2 双线性插值上采样

        转置卷积能够扩大尺寸细化特征图，但会导致棋盘效应——转置卷积不均匀重叠，中间部分的像素重叠过多，形成类似棋盘格的像素块。                                                                                           使用双线性插值先将图片扩大，在用卷积即解决转置卷积问题，优化图像。       

1.2.1方法介绍

        采用拉格朗日插值法中的线性插值中的两点对称式直线方程。

        由已知（x0,y0）,（x1,y1）两点列出等式，代入x0，x1之间任意点x至等式，可以得到对应y值。

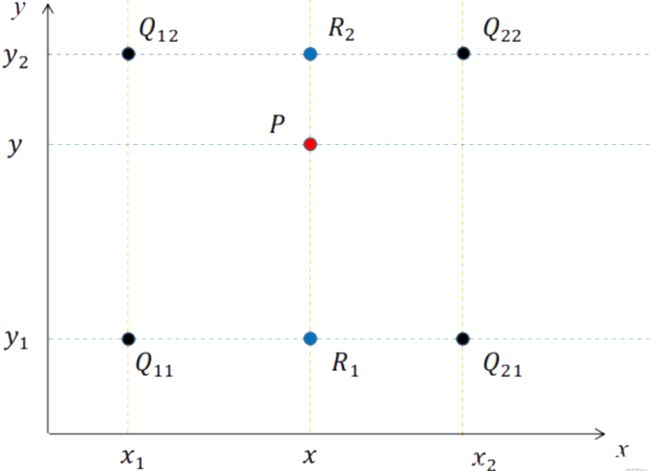
1.2.2双线性插值法

        通过进行两个方向的插值。首先对x方向进行两次插值得到R1和R2的坐标，再由两点进行y方向的插值。得到新的等式，将点的x坐标代入可得到y值。

​

1.2.3代码

        代码3 ：双线性插值法

import cv2
import numpy as np
def bilinear_interpolation(img, out_dim):
    src_h, src_w, channel = img.shape  # 原图片的高、宽、通道数
    dst_h, dst_w = out_dim[1], out_dim[0]  # 输出图片的高、宽
    print('src_h,src_w=', src_h, src_w)
    print('dst_h,dst_w=', dst_h, dst_w)
    if src_h == dst_h and src_w == dst_w:
        return img.copy()
    dst_img = np.zeros((dst_h, dst_w, 3), dtype=np.uint8)
    scale_x, scale_y = float(src_w) / dst_w, float(src_h) / dst_h
    for i in range(3):  # 指定 通道数，对channel循环
        for dst_y in range(dst_h):  # 指定 高，对height循环
            for dst_x in range(dst_w):  # 指定 宽，对width循环
                # 源图像和目标图像几何中心的对齐
                # src_x = (dst_x + 0.5) * srcWidth/dstWidth - 0.5
                # src_y = (dst_y + 0.5) * srcHeight/dstHeight - 0.5
                src_x = (dst_x + 0.5) * scale_x - 0.5
                src_y = (dst_y + 0.5) * scale_y - 0.5
                # 计算在源图上四个近邻点的位置
                src_x0 = int(np.floor(src_x))
                src_y0 = int(np.floor(src_y))
                src_x1 = min(src_x0 + 1, src_w - 1)
                src_y1 = min(src_y0 + 1, src_h - 1)
                # 双线性插值
                temp0 = (src_x1 - src_x) * img[src_y0, src_x0, i] + (src_x - src_x0) * img[src_y0, src_x1, i]
                temp1 = (src_x1 - src_x) * img[src_y1, src_x0, i] + (src_x - src_x0) * img[src_y1, src_x1, i]
                dst_img[dst_y, dst_x, i] = int((src_y1 - src_y) * temp0 + (src_y - src_y0) * temp1)
    return dst_img
img = cv2.imread(r'C:\Users\1\Desktop\1\1.jpg')      # 修改图像所在的位置
dst = bilinear_interpolation(img, (1500, 1500))      # 图像的输出大小 
cv2.imshow("blinear", dst)
cv2.waitKey()
cv2.imwrite("13.jpg",img)    #将图片保存为jpg

1.3反池化上采样

1.3.1反池化介绍

        经过下采样时，最大池化会记录池化的索引，索引代表取得值所在的位置。在反池化时，将输入值根据索引放回原来的位置，得到一个元素多为0的稀疏矩阵。

1.3.2优点

        反池化的操作，索引记录了更多的边缘信息，可以加强刻画物体的能力，通过重用这些边缘信息，加强精确的边界位置信息。在分割的时候有助于产生更平滑的分割。

1.3.3代码

        代码4 ：反池化

import torch
import torch.nn as nn
test = torch.rand((2, 3, 128, 128))
print("Original Size -> ", test.size())
# maxPool池化
maxpool = nn.MaxPool2d(2, 2)
# 设定要返回索引
maxpool.return_indices = True
# 记录池化结果，索引结果
mp, indices = maxpool(test)
print("MaxPool -> ", mp.size())
# 设置MaxUnpool反池化
unpooling = nn.MaxUnpool2d((2, 2), stride=2)
# 传入参数和索引
upsamle = unpooling(mp, indices)
print("MaxUnpool -> ", upsamle.size())

二.参考资料

感谢

博客——博主：哈土奇

数值分析——辽宁工程技术大学胡行华等