机器学习实验 - 集成学习（AdaBoost、Bagging、随机森林）

报告内容仅供学习参考，请独立完成作业和实验喔~

一、报告摘要

1.1 实验要求

（1）掌握集成学习思想，掌握boosting和bagging策略;
（2）基于Adaboost实现多分类任务；
（3）参考随机森林，以决策树为基学习器，构建bagging集成器用于多分类任务。

1.2 实验思路

\qquad 使用Python编写Adaboost和Bagging算法框架，并利用sklearn提供的基学习器构建Adaboost和Bagging算法模型，读取Iris数据集信息并进行多分类预测，调整超参数优化模型，并根据精确率、召回率和F1值度量模型性能。

1.3 实验结论

\qquad 本实验使用决策树作为基学习器，结合编写的Adaboost和Bagging算法训练了两个集成学习多分类模型，并通过计算精确率、召回率和F1值度量模型性能。其中，得到最好分类效果的模型的精确率为0.97143，召回率为0.96667，F1值为0.96737。

二、实验内容

2.1 方法介绍

（1）集成学习
\qquad 集成学习（Ensemble learning）通过构建并结合多个学习其来完成学习任务，也被称为多分类器系统或基于委员会的学习系统等。
\qquad 集成学习的一般结构是先构建一组“个体学习器”，随后再利用某种策略将这些“个体学习器”结合起来得到集成学习的结果。其中的个体学习器一般使用决策树等较通用的现成算法，使用训练数据集训练得到。

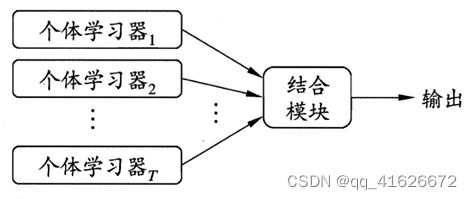
\qquad 根据个体学习器的种类是否相同，集成学习可以分为同质集成和异质集成。同质集成中只包含同种类型的个体学习器，此时个体学习器也被称为基学习器，对应的学习算法被称为基学习算法；异质集成中的个体学习器种类不同，由不同的学习算法生成，此时的个体学习器一般不称为基学习器，而是称为组件学习器或直接叫个体学习器。
\qquad 根据个体生成器的生成方式，集成学习方法可以分为两大类。分别为个体学习器之间存在强依赖关系、必须串行生成的序列化方法，例如Boosting；以及个体学习器之间不存在强依赖关系、可以同时生成的并行化方法，例如Bagging和随机森林。
\qquad 由于集成学习是通过将多个学习器进行结合，故常常可以获得比单独某个学习器更显著和优越的效果。原因很简单，在集成学习中，结果一般采用投票法生成，也就是对于每一个数据，其结果是全部个体学习器给出的结果按少数服从多数的思想去集成得到。对于二分类问题，如果单独一个学习器的准确率为60%，也就是错误率为40%，那假设有10个个体学习器，有一半学习器判断错误的概率就是$C_{10}^5\ast {0.4}^5\ast {0.6}^5\approx 0.2006$，错误率明显降低。
\qquad 下面给出数学公式证明：对于二分类问题$y\in -1,+1$和真实函数$f$，假定每个基分类器的错误率为$ϵ$，即对于每个基分类器$h_i$，均有
$$P\left(h_i\ne f\left(x\right)\right)=ϵ$$
\qquad 假设集成学习通过简单投票法（少数服从多数）结合T个基分类器，只要有超过半数的基分类器判断正确，则整体的集成学习分类就是正确的，即
$$H\left(x\right)=sign(\sum _{i=1}^T{h}_i(x))$$
\qquad 假设每个基分类器之间错误率相互独立，则由霍夫丁Hoeffding不等式可得集成学习的错误率如下
$$P\left(H\left(x\right)\ne f\left(x\right)\right)=\sum _{k=0}^{\lfloor T/2\rfloor }\left(\begin{array}{c}K\\ k\end{array}\right){(1-ϵ)}^k{ϵ}^{T-k}\le \exp (-\frac{1}{2}T{\left(1-2ϵ\right)}^2)$$
\qquad 根据上述推导公式可知，随着基学习器数量T的增大，集成学习的整体错误率也将指数级降低，最终趋向于0。
（2）Boosting
\qquad Boosting是一类可以将弱学习器提升为强学习器的算法。
\qquad Boosting的工作机制基本相同：首先从初始训练集中训练出一个基学习器，随后根据基学习器的性能表现对训练样本的分布进行一定的调整，增强对错误样本的关注度；随后基于调整后的样本分布来训练下一个基学习器；持续迭代当前过程，直至基学习器数目达到预先设定的值；最终将全部基学习器进行加权集合，训练完成。
\qquad Boosting算法中具代表性的算法为Adaboost算法。Adaboost算法可以通过使得基学习器线性组合后最小化指数损失函数来推导得到，具体算法步骤如下：
\qquad a. 初始化样本权值分布为1/m.
\qquad b. 迭代基分类器。对于每个基分类器，先基于当前样本权值分布$D_t$从数据集D中训练出分类器$h_t$，并估计$h_t$的误差；根据误差计算分类器$h_t$的权重${\alpha }_t$，计算公式如下：
$${\alpha }_t=\frac{1}{2}ln(\frac{1-{ϵ}_t}{{ϵ}_t})$$
\qquad 完成后更新样本分布$D_{t+1}(x)$，并进行规范化

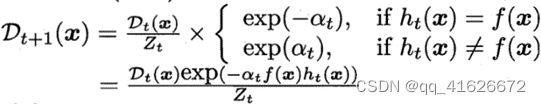
\qquad 最终输出结果如下
$$H(x)=sign(\sum _{t=1}^T{\alpha }_t{h}_t(x))$$
\qquad 但标准的Adaboost算法只能实现二分类任务，或者说，利用标准Adaboost算法直接进行多分类任务很难取得较好的结果。因此要想实现多分类，可以采用改进的SAMME或SAMME.R算法。
\qquad SAMME算法过程如下：

\qquad 根据算法过程也能看出，SAMME与标准Adaboost非常相似，只是增加了$log(K-1)$这个一项。因此，当K=2时，SAMME等同于Adaboost。
\qquad SAMME.R算法过程如下：

\qquad 与SAMME算法不同，SAMME.R算法采用加权概率估计（weighted probability estimates）的方法更新加法模型。相比来说，SAMME.R算法使用了比SAMME算法更多的信息，也可以获得更高的准确率和鲁棒性。
（3）Bagging
\qquad 在（1）已经证明过，在基学习器相互独立的情况下，集成学习器的误差随着学习器数量的增多呈指数级的下降。但是，使用相同类型的基学习器处理相同的问题，几乎不可能做到相互独立。因此可以在数据上进行处理，即对相同训练样本进行采样，产生出若干个不同的子集，再使用每个子集分别训练基学习器。当采样方法恰当时，由于训练数据不同，获得的基学习器会有比较大的差异，同时可以取得较好的结果。
\qquad Bagging算法基于自助采样法，也可以理解为有放回重新采样法，即给定一个包含m个样本点的数据集，每次取出样本放入采样集中，再把样本放回原始数据集，使得下次采样时仍然可以选中这个样本。经过m次采样操作，可以得到含m个样本的采样机，初始训练集中有的样本在采样集里多次出现，有的从未出现过，理论上会有63.2%的样本出现在采样集中，约有36.8%样本可以用在验证。
\qquad 重复上述过程，可以采样出T个含m个训练样本的采样集，随后对每个采样集训练出一个基学习器，再将基学习器进行结合。Bagging中对于分类任务采用简单投票法（少数服从多数），对于回归任务采用简单平均法（几何平均）。分类任务中出现同票情况时，采用随机选择或者进一步考察分类器投票置信度来决定。
\qquad Bagging的算法描述如下图：

2.2 实验细节

2.2.1 实验环境

硬件环境：Intel® Core™ i5-10300H CPU + 16G RAM
软件环境：Windows 11 家庭中文版 + Python 3.8

2.2.2 实验过程

（1）Adaboost-SAMME算法
\qquad 根据2.1（2）中的算法描述，SAMME算法首先初始化权重。随后进行M次迭代，每次迭代需要训练基分类并进行预测，根据预测结果计算错误率，并根据错误率调整样本分布情况，最后根据处理分类器权重并归一，完成本次迭代。
\qquad 具体代码实现及注释如下：

def boost_SAMME(self, X, y, sample_weight): # SAMME
        estimator = deepcopy(self.base_estimator_)
        if self.random_state_:
            estimator.set_params(random_state=1)
        # (a)训练基分类器，计算结果
        estimator.fit(X, y, sample_weight=sample_weight)
        y_pred = estimator.predict(X)
        incorrect = y_pred != y
        # (b)计算错误率
        estimator_error = np.dot(incorrect, sample_weight) / np.sum(sample_weight, axis=0)
        # 分类效果比随机数还差，抛弃这种情况
        if estimator_error >= 1 - 1 / self.n_classes_:
            return None, None, None
        # (c)(1)计算当前分类器权重
        estimator_weight = self.learning_rate_ * np.log((1 - estimator_error) / estimator_error) + np.log(
            self.n_classes_ - 1)
        # 权重为负，无意义，抛弃
        if estimator_weight <= 0:
            return None, None, None
        # (d) 更新样本权重
        sample_weight *= np.exp(estimator_weight * incorrect)
        sample_weight_sum = np.sum(sample_weight, axis=0)
        if sample_weight_sum <= 0:
            return None, None, None
        # (e)归一化权重
        sample_weight /= sample_weight_sum
        # 存储当前弱分类器
        self.estimators_.append(estimator)
        return sample_weight, estimator_weight, estimator_error

（2）Adaboost-SAMME.R算法
\qquad 根据2.1（2）中的算法描述，SAMME.R算法首先初始化权重。随后进行M次迭代，每次迭代需要训练及分类并进行预测，随后根据预测结果计算加权概率估计h(x)，再根据h(x)的值调整样本分布情况及分类器权重并归一化处理。
\qquad 具体代码实现及注释如下：

 def boost_SAMMER(self, X, y, sample_weight): # SAMME.R
        estimator = deepcopy(self.base_estimator_)
        if self.random_state_:
            estimator.set_params(random_state=1)
        # 训练弱分类器
        estimator.fit(X, y, sample_weight=sample_weight)
        # 计算错误率
        y_pred = estimator.predict(X)
        incorrect = y_pred != y
        estimator_error = np.dot(incorrect, sample_weight) / np.sum(sample_weight, axis=0)
        # 比随机猜还差，抛弃
        if estimator_error >= 1.0 - 1 / self.n_classes_:
            return None, None, None
        # 计算h(x)
        y_predict_proba = estimator.predict_proba(X)
        y_predict_proba[y_predict_proba < np.finfo(y_predict_proba.dtype).eps] = np.finfo(y_predict_proba.dtype).eps

        y_codes = np.array([-1. / (self.n_classes_ - 1), 1.])
        y_coding = y_codes.take(self.classes_ == y[:, np.newaxis])
        # 更新样本权重
        intermediate_variable = (-1. * self.learning_rate_ * (((self.n_classes_ - 1) / self.n_classes_) *
                                                              inner1d(y_coding, np.log(
                                                                  y_predict_proba)))) 
        sample_weight *= np.exp(intermediate_variable)
        sample_weight_sum = np.sum(sample_weight, axis=0)
        if sample_weight_sum <= 0:
            return None, None, None
        # 归一化权重
        sample_weight /= sample_weight_sum
        # 存储当前弱分类器
        self.estimators_.append(estimator)
        return sample_weight, 1, estimator_error

（3）手写Bagging实现随机森林算法
\qquad 根据自助采样法定义，每次从m个样本中随机有放回的取出m个样本构成新的数据集，得到如下代码实现：

def randomSample(X,y, rate):  # 自助采样法,data为原始数据集，rate为采样比例（应该为1）
    X_train = []
    y_train = []
    for i in range(int(len(X)*rate)):
        rand_num = random.randint(0, len(X) - 1)
        X_train.append(X[rand_num])
        y_train.append(y[rand_num])
    return X_train,y_train

\qquad 对Bagging算法的训练过程其实就是对若干个基分类器使用不同的数据子集进行训练的过程，代码实现如下：

def bagging(X,y,rate,n_estimators,base_estimator): # 数据X、y，rate=1，分类器个数
    print("开始训练Bagging")
    global estimators
    for i in range(n_estimators): # 构建N个分类器
        tmp_estimator = deepcopy(base_estimator)
        X_train,y_train = randomSample(X,y,rate)
        tmp_estimator.fit(X_train,y_train)
        estimators.append(tmp_estimator)
    print("弱分类器已完成训练")

\qquad 利用Bagging对数据进行分类其实就是把数据给全部基分类器进行分类，最后对得到的结果进行投票，少数服从多数得到结果，代码实现如下：

def predict(X):
    print("开始进行分类")
    global estimators
    result = []
    sample_result = []
    for estimator in estimators: # 求每一个分类器的结果
        result.append(list(estimator.predict(X)))
    n = len(result[0])
    for i in range(n): # 投票过程
        counter = Counter(list(np.array(result)[:,i]))
        tmp = counter.most_common()
        sample_result.append(tmp[0][0])
    return sample_result

（4）使用sklearn验证随机森林算法
\qquad 以决策树作为基学习器，设置随机森林的基学习器个数n_estimators=4，使用Iris数据集的80%为训练集，构建随机森林模型。
\qquad 代码实现上，利用sklearn提供的RandomForestClassifier()方法完成。sklearn中的RandomForestClassifier()方法通过使用多组不同数据子集来训练多颗决策树，再通过投票法完成分类。常用参数如下：

基分类器数量n_estimators：默认为100
最大深度max_depth：基分类器决策树的最大深度
并行作业数n_jobs：默认为1，决定同时并行训练的基分类器个数
其他控制基分类器的参数与决策树DesicionTreeClassifier()方法相同。

\qquad 具体实现的核心代码如下：

X, y = datasets.load_iris(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X, y, test_size = 0.2, random_state = 1)
random_forest = RandomForestClassifier(n_estimators=4)
random_forest.fit(X_train,y_train)

2.3 实验数据介绍

\qquad 实验数据为来自UCI的鸢尾花三分类数据集Iris Plants Database。
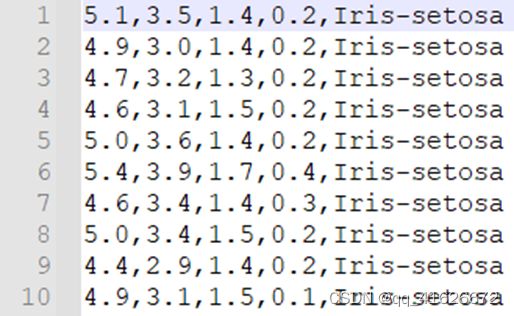
\qquad 数据集共包含150组数据，分为3类，每类50组数据。每组数据包括4个参数和1个分类标签，4个参数分别为：萼片长度sepal length、萼片宽度sepal width、花瓣长度petal length、花瓣宽度petal width，单位均为厘米。分类标签共有三种，分别为Iris Setosa、Iris Versicolour和Iris Virginica。
\qquad 数据集格式如下图所示：

\qquad 为方便使用，也可以直接调用sklearn.datasets库中提供的load_iris()方法加载处理过的鸢尾花分类数据集。

2.4 评价指标介绍

\qquad 评价指标选择精确率P、召回率R、F1度量值F1，计算公式如下：
$$P=\frac{TP}{TP+FP}$$
$$R=\frac{TP}{TP+FN}$$
$$F1=\frac{2\ast P\ast R}{P+R}$$
\qquad 具体代码实现时，可以直接调用sklearn库中的相应方法进行计算。

2.5 实验结果分析

\qquad 根据计算，对于鸢尾花数据集，在使用相同的随机数种子进行数据集划分后（random_state=23333），可以得到如下结果：

使用方法	Adaboost-SAMME(n=4)	Adaboost-SAMME.R(n=4)	手写Bagging(n=4)	RandomForest(n=4)
精确率P	0.95	0.97143	0.96875	0.97143
召回率R	0.93333	0.96667	0.96667	0.96667
F-Score(β=1)	0.93571	0.96737	0.96569	0.96737

\qquad 根据上述数据可知，在使用相同数据集的情况下，以上4种集成学习的算法均可以取得较好的分类效果。其中的手写和sklearn实现的RandomForest方法均因为不同的数据子集取样方法得到不同的性能指标，F1值在0.96上下波动。

三、总结及问题说明

\qquad 本次实验的主要内容为使用Adaboost和Bagging两类集成学习方法对鸢尾花数据集进行多分类预测，并调整参数，计算生成模型的精确度Precision、召回率Recall和F1度量值，从而对得到的模型进行评测，弄清参数与效果之间的关系，对两种集成学习有更深的理解。
\qquad 在本次实验中，未遇到很难解决的问题，可以按要求完成分类任务。

四、参考文献

[1] 周志华. 机器学习[M]. 清华大学出版社, 2016.
[2] Hastie T, Rosset S, Zhu J, et al. Multi-class adaboost[J]. Statistics and its Interface, 2009, 2(3): 349-360.
[3] jinxin0924/multi-adaboost [EB/OL]. [2022-5-25]. https://github.com/jinxin0924/multi-adaboost.
[4] sklearn.ensemble.RandomForestClassifier — scikit-learn 1.1.1 documentation [EB/OL]. [2022-5-25]. https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html.
[5] 【机器学习】Adaboost多类分类——SAMME算法，SAMME.R算法[EB/OL]. [2022-5-25]. https://blog.csdn.net/weixin_43298886/article/details/110927084.
[6] Multi-class AdaBoost learning experience [EB/OL]. [2022-5-25]. https://www.jianshu.com/p/1855b411794c.
[7] 机器篇——集成学习(一) 细说 Bagging 算法 [EB/OL]. [2022-5-25]. https://blog.csdn.net/qq_38299170/article/details/103833113.

附录：实验代码

'''
AdaBoostClassifier
参考来源：https://github.com/jinxin0924/multi-adaboost
Author:jinxin0924、CrayonDing
'''
import numpy as np
from numpy.core.umath_tests import inner1d
from copy import deepcopy

class AdaBoostClassifier(object):
    def __init__(self, *args, **kwargs):
        if kwargs and args:
            raise ValueError(
                '''AdaBoostClassifier can only be called with keyword
                   arguments for the following keywords: base_estimator ,n_estimators,
                    learning_rate,algorithm,random_state''')
        allowed_keys = ['base_estimator', 'n_estimators', 'learning_rate', 'algorithm', 'random_state']
        keywords_used = kwargs.keys()
        for keyword in keywords_used:
            if keyword not in allowed_keys:
                raise ValueError(keyword + ":  Wrong keyword used --- check spelling")

        n_estimators = 50
        learning_rate = 1
        algorithm = 'SAMME.R'
        random_state = None

        if kwargs and not args:
            if 'base_estimator' in kwargs:
                base_estimator = kwargs.pop('base_estimator')
            else:
                raise ValueError('''base_estimator can not be None''')
            if 'n_estimators' in kwargs: n_estimators = kwargs.pop('n_estimators')
            if 'learning_rate' in kwargs: learning_rate = kwargs.pop('learning_rate')
            if 'algorithm' in kwargs: algorithm = kwargs.pop('algorithm')
            if 'random_state' in kwargs: random_state = kwargs.pop('random_state')

        self.base_estimator_ = base_estimator
        self.n_estimators_ = n_estimators
        self.learning_rate_ = learning_rate
        self.algorithm_ = algorithm
        self.random_state_ = random_state
        self.estimators_ = list()
        self.estimator_weights_ = np.zeros(self.n_estimators_)
        self.estimator_errors_ = np.ones(self.n_estimators_)

    def _samme_proba(self, estimator, n_classes, X): # 计算h(x)
        # 2(b)
        proba = estimator.predict_proba(X)
        proba[proba < np.finfo(proba.dtype).eps] = np.finfo(proba.dtype).eps
        log_proba = np.log(proba)
        return (n_classes - 1) * (log_proba - (1. / n_classes)
                                  * log_proba.sum(axis=1)[:, np.newaxis])

    def fit(self, X, y):
        self.n_samples = X.shape[0]
        self.classes_ = np.array(sorted(list(set(y))))
        self.n_classes_ = len(self.classes_)
        for iboost in range(self.n_estimators_):
            if iboost == 0: # 初始化权重为1/n
                sample_weight = np.ones(self.n_samples) / self.n_samples
            # 循环迭代弱分类器
            sample_weight, estimator_weight, estimator_error = self.boost(X, y, sample_weight)
            # 提前结束，训练失败
            if estimator_error == None:
                break
            # 存储弱分类器权重
            self.estimator_errors_[iboost] = estimator_error
            self.estimator_weights_[iboost] = estimator_weight
            if estimator_error <= 0:
                break
        return self

    def boost(self, X, y, sample_weight):
        if self.algorithm_ == 'SAMME':
            return self.boost_SAMME(X, y, sample_weight)
        elif self.algorithm_ == 'SAMME.R':
            return self.boost_SAMMER(X, y, sample_weight)

    def boost_SAMMER(self, X, y, sample_weight): # SAMME.R
        estimator = deepcopy(self.base_estimator_)
        if self.random_state_:
            estimator.set_params(random_state=1)
        # 训练弱分类器
        estimator.fit(X, y, sample_weight=sample_weight)
        # 计算错误率
        y_pred = estimator.predict(X)
        incorrect = y_pred != y
        estimator_error = np.dot(incorrect, sample_weight) / np.sum(sample_weight, axis=0)
        # 比随机猜还差，抛弃
        if estimator_error >= 1.0 - 1 / self.n_classes_:
            return None, None, None
        # 计算h(x)
        y_predict_proba = estimator.predict_proba(X)
        y_predict_proba[y_predict_proba < np.finfo(y_predict_proba.dtype).eps] = np.finfo(y_predict_proba.dtype).eps
        y_codes = np.array([-1. / (self.n_classes_ - 1), 1.])
        y_coding = y_codes.take(self.classes_ == y[:, np.newaxis])
        # 更新样本权重
        intermediate_variable = (-1. * self.learning_rate_ * (((self.n_classes_ - 1) / self.n_classes_) *inner1d(y_coding, np.log(y_predict_proba))))
        sample_weight *= np.exp(intermediate_variable)
        sample_weight_sum = np.sum(sample_weight, axis=0)
        if sample_weight_sum <= 0:
            return None, None, None
        # 归一化权重
        sample_weight /= sample_weight_sum
        # 存储当前弱分类器
        self.estimators_.append(estimator)
        return sample_weight, 1, estimator_error

    def boost_SAMME(self, X, y, sample_weight): # SAMME
        estimator = deepcopy(self.base_estimator_)
        if self.random_state_:
            estimator.set_params(random_state=1)
        # (a)训练基分类器，计算结果
        estimator.fit(X, y, sample_weight=sample_weight)
        y_pred = estimator.predict(X)
        incorrect = y_pred != y
        # (b)计算错误率
        estimator_error = np.dot(incorrect, sample_weight) / np.sum(sample_weight, axis=0)
        # 分类效果比随机数还差，抛弃这种情况
        if estimator_error >= 1 - 1 / self.n_classes_:
            return None, None, None
        # (c)(1)计算当前分类器权重
        estimator_weight = self.learning_rate_ * np.log((1 - estimator_error) / estimator_error) + np.log(
            self.n_classes_ - 1)
        # 权重为负，无意义，抛弃
        if estimator_weight <= 0:
            return None, None, None
        # (d) 更新样本权重
        sample_weight *= np.exp(estimator_weight * incorrect)
        sample_weight_sum = np.sum(sample_weight, axis=0)
        if sample_weight_sum <= 0:
            return None, None, None
        # (e)归一化权重
        sample_weight /= sample_weight_sum
        # 存储当前弱分类器
        self.estimators_.append(estimator)
        return sample_weight, estimator_weight, estimator_error

    def predict(self, X):
        n_classes = self.n_classes_
        classes = self.classes_[:, np.newaxis]
        pred = None
        if self.algorithm_ == 'SAMME.R':
            # SAMME.R权重均为1
            pred = sum(self._samme_proba(estimator, n_classes, X) for estimator in self.estimators_)
        else:  # SAMME
            pred = sum((estimator.predict(X) == classes).T * w
                       for estimator, w in zip(self.estimators_,
                                               self.estimator_weights_))
        pred /= self.estimator_weights_.sum()
        if n_classes == 2:
            pred[:, 0] *= -1
            pred = pred.sum(axis=1)
            return self.classes_.take(pred > 0, axis=0)
        return self.classes_.take(np.argmax(pred, axis=1), axis=0)

    def predict_proba(self, X):
        if self.algorithm_ == 'SAMME.R':
            # SAMME.R权重均为1
            proba = sum(self._samme_proba(estimator, self.n_classes_, X)
                        for estimator in self.estimators_)
        else:  # SAMME
            proba = sum(estimator.predict_proba(X) * w
                        for estimator, w in zip(self.estimators_,
                                                self.estimator_weights_))
        proba /= self.estimator_weights_.sum()
        proba = np.exp((1. / (self.n_classes_ - 1)) * proba)
        normalizer = proba.sum(axis=1)[:, np.newaxis]
        normalizer[normalizer == 0.0] = 1.0
        proba /= normalizer
        return proba

'''
Adaboost算法测试
Author:CrayonDing
'''
from sklearn import datasets
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier

X, y = datasets.load_iris(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=23333) # 随机数种子设置为相同
print('数据集样本数：{},训练样本数：{},测试集样本数：{}'.format(len(X),len(X_train),len(X_test)))

from multi_AdaBoost import AdaBoostClassifier as Ada

SAMMER = Ada(
    base_estimator=DecisionTreeClassifier(max_depth=2),
    n_estimators=4,
    learning_rate=1)
SAMMER.fit(X_train, y_train)

SAMME = Ada(
    base_estimator=DecisionTreeClassifier(max_depth=2),
    n_estimators=4,
    learning_rate=1,
    algorithm='SAMME')
SAMME.fit(X_train, y_train)

print("SAMME")
y_pred = SAMME.predict(X_test)
print("精确率",precision_score(y_test, y_pred, average='weighted'))
print("召回率",recall_score(y_test, y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, y_pred, average='weighted'))

print("SAMME.R")
r_y_pred = SAMMER.predict(X_test)
print("精确率",precision_score(y_test, r_y_pred, average='weighted'))
print("召回率",recall_score(y_test, r_y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, r_y_pred, average='weighted'))

'''
Bagging框架实现
Author:CrayonDing
'''
from sklearn import tree
import numpy as np
import random
from sklearn.model_selection import train_test_split
from sklearn.metrics import precision_score, recall_score, f1_score
from sklearn import datasets
from copy import deepcopy
from collections import Counter

def randomSample(X,y, rate):  # 自助采样法,data为原始数据集，rate为采样比例
    X_train = []
    y_train = []
    for i in range(int(len(X)*rate)):
        rand_num = random.randint(0, len(X) - 1)
        X_train.append(X[rand_num])
        y_train.append(y[rand_num])
    return X_train,y_train

estimators = []
def bagging(X,y,rate,n_estimators,base_estimator): # 数据X、y，每次的采样率，分类器个数
    print("开始训练Bagging")
    global estimators
    for i in range(n_estimators): # 构建N个分类器
        #print("第"+str(i)+"个弱分类器")
        tmp_estimator = deepcopy(base_estimator)
        X_train,y_train = randomSample(X,y,rate)
        tmp_estimator.fit(X_train,y_train)
        estimators.append(tmp_estimator)
        #print(tmp_estimator)
    print("弱分类器已完成训练")

def predict(X):
    print("开始进行分类")
    global estimators
    result = []
    sample_result = []

    for estimator in estimators: # 求每一个分类器的结果
        result.append(list(estimator.predict(X)))
        #print(list(estimator.predict(X)))

    n = len(result[0])
    for i in range(n):
        counter = Counter(list(np.array(result)[:,i]))
        tmp = counter.most_common()
        # print(tmp[0][0])
        sample_result.append(tmp[0][0])
    # print(sample_result)
    return sample_result

X, y = datasets.load_iris(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X, y, test_size = 0.2, random_state = 23333)

base_estimator = tree.DecisionTreeClassifier(criterion='gini',max_depth=5,splitter='best')
bagging(X_train,y_train,1,4,base_estimator)
y_pred = predict(X_test)

print("精确率",precision_score(y_test, y_pred, average='weighted'))
print("召回率",recall_score(y_test, y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, y_pred, average='weighted'))

'''
sklearn 随机森林模型测试
Author:CrayonDing
'''
%matplotlib inline
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
from sklearn.metrics import precision_score, recall_score, f1_score
from sklearn import datasets
from sklearn.model_selection import train_test_split

X, y = datasets.load_iris(return_X_y=True)
X_train,X_test,y_train,y_test = train_test_split(X, y, test_size = 0.2, random_state = 23333) # 随机数种子相同，保证数据集一样

random_forest = RandomForestClassifier(n_estimators=4) # 训练随机森林模型
random_forest.fit(X_train,y_train)

y_pred = random_forest.predict(X_test)
print("精确率",precision_score(y_test, y_pred, average='weighted'))
print("召回率",recall_score(y_test, y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, y_pred, average='weighted'))