《图算法》第五章 中心性算法-1

对图算法有兴趣的朋友可以关注微信公众号 ：《 Medical与AI的故事》

原文链接：《图算法》第五章-1 中心性算法

中心性算法（centrality algorithm）用于理解图中特定节点的角色及其对网络的影响。之所以有用，是因为这些算法能够识别最重要的节点，并帮助我们了解群体动态，例如可信度、可访问性、事物传播的速度以及群体之间的桥梁。尽管这些算法中有许多是为社交网路分析而发明的，但它们已经在各种行业和领域中得到了应用。
我们将介绍以下算法：

• 度中心性(Degree Centrality)作为连通性的基线度量
• 紧密中心性（Closeness Centrality）用于测量节点对群体的意义，包括对断开连接群体的两个变体
• 中介中心性（Betweenness Centrality）用于查找控制点，包括一个近似的估计算法
• 网页排名（PageRank）用来了解整体性的影响，包括一个个性化的网页排名变体
  不同的中心性算法所用的度量值均不同，因而会在算法之间差生显著的差异结果。当你看到次优答案的时候，最好检查一下你使用的算法是否符合它的预期目的。我们将解释这些算法如何工作，并在Spark和Neo4j中运行示例。如果一个算法在一个平台上不可用，或者平台之间的差异并不重要，我们将只提供一个平台上的示例。

图5-1显示了中心性算法可以回答的问题类型之间的差异，表5-1是每个算法使用示例计算的快速参考。

图5-1.有代表性的中心性算法及其回答的问题类型
表5-1.中心性算法概述


一些中心性算法计算每对节点之间的最短路径。这对中小型图很有效，但是对于大型图来说，计算上是不允许的。为了避免大型图上的长运行时间，一些算法（例如，中间中心性）有估算版本。

首先，我们将为我们的示例描述数据集，并将数据导入Apache Sark和Neo4j中，按表5-1中列出的顺序介绍各个算法。我们将从对算法的简短描述开始，并在有必要时提供有关它如何操作的原理性信息。对于涉及到的变种算法，将会只做简要描述。大多数章节还包括有关相关算法的使用场景指导。我们在每个部分的末尾，在示例数据集上演示示例代码。

让我们开始吧！

图数据示例：社交图

中心性算法与所有领域的图都相关，但是社交网络提供了一种非常相关的方式来考虑动态影响和信息流向。本章中的例子是在一个类似Twitter的小规模图上运行的。您可以从Github上下载节点和关系文件，我们将用它们来创建图。
表5-2 social-node.csv

表5-3 social-relationships.csv

图5-2展现了我们想要构建的图。

图5-2.图模型

图中有一个较大的用户集，它们之间有连接，而另外一部分较小的用户组没有连接到较大的用户组上，它们相互之间是断开的。基于这些csv文件的内容，我们将在在Spark和Neo4j中创建图。

将数据导入Apache Spark

首先，我们将需要的包从Spark和GraphFrames中导入

from graphframes import *
from pyspark import SparkContext

我们可以用如下的代码来根据csv文件创建一个GraphFrame

base = "file:///home/retire2053/source/graph_algorithms_resources/"
v = spark.read.csv(base+"data/social-nodes.csv", header=True)
e = spark.read.csv(base+"data/social-relationships.csv", header=True)
g = GraphFrame(v, e)

将数据导入Neo4j

接下来，我们将数据装载到Neo4j，以下查询语句用来导入节点。

WITH "https://github.com/neo4j-graph-analytics/book/raw/master/data/" AS base
WITH base + "social-nodes.csv" AS uri
LOAD CSV WITH HEADERS FROM uri AS row
MERGE (:User {id: row.id})

然后是导入关系

WITH "https://github.com/neo4j-graph-analytics/book/raw/master/data/" AS base
WITH base + "social-relationships.csv" AS uri
LOAD CSV WITH HEADERS FROM uri AS row
MATCH (source:User {id: row.src})
MATCH (destination:User {id: row.dst})
MERGE (source)-[:FOLLOWS]->(destination)

现在，我们的图已经被装载了，是开始使用算法的时候了。

度中心性(Degree Centrality)

度中心性是我们将在本书中讨论的最简单的算法。它计算节点上传入和传出关系的数量，该算法可以用于在图中查找”热"（poplular）的节点。度中心性是Linton C. Freeman在1979年的论文“Centrality in Social Networks: Conceptual Clarification”中提出的。

到达范围（Reach）

节点的到达范围（reach）是衡量重要性的合理标准。一个节点能接触到多少个其他节点？一个节点的度（Degree）是它所具有的直接关系的数目，包括入度数和出度数。你可以将度视为该节点的直接到达节点。例如，一个在活跃的社交网络中很高节点度数的人会有很多直接的接触，因此而通常更容易得感冒一些。

网络的平均度（average degree）只是关系总数除以节点总数；平均度数容易被高度节点严重扭曲，也就是低度节点容易被平均。度分布（degree distribution）是被随机选择的节点具有某个度数的概率。

图5-3说明了Subreddit上，主题之间连接的实际分布的差异。如果你简单地取平均值，你会假设大多数主题有10个连接，而实际上大多数主题只有2个连接。

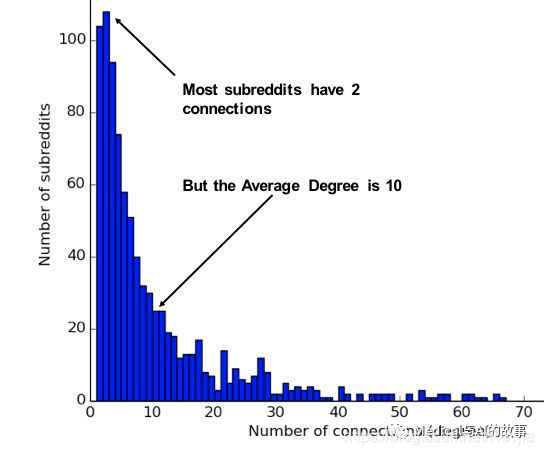
图5-3.Jacob Silterrapa绘制的这张Subreddit度分布图提供了一个例子，说明平均值通常不反映网络中的实际分布。CC BY-SA 3.0。
这些评估用于对网络类型进行分类，如第2章讨论的自由缩放（Scale-free）或小世界（small world）网络。它们还提供了一个快速的措施来帮助估计事物在网络中传播或波动的可能性。

度中心性算法的使用场景

如果您试图通过查看传入和传出关系的数量来分析影响，或者找到单个节点的“流行度”，请使用“度中心性”。当你关注即时连通性时，它会很好地工作。不仅仅于此，当您想要评估整个图的最小程度、最大程度、平均程度和标准偏差时，度中心性也应用于全局分析。
示例用例包括：

• 通过人际关系识别有权势的个人，例如社交网络中的人际关系。例如，在BrandWatch的“Most Influential Men and
  Women on Twitter 2017”中，每个类别的前5名都有超过4000万名粉丝。
• 将欺诈者与在线拍卖网站的合法用户分开。欺诈者的加权中心性倾向于明显更高，因为他们的目的是人为地提高价格。阅读P.
  Bangcharoensap等人的论文Two Step Graph-Based Semi-Supervised Learning for
  Online Auction Fraud Detection。

在Apache Spark上的度中心性算法

现在，我们用如下的代码来执行度中心性算法

total_degree = g.degrees
in_degree = g.inDegrees
out_degree = g.outDegrees
(total_degree.join(in_degree, "id", how="left")
.join(out_degree, "id", how="left")
.fillna(0)
.sort("inDegree", ascending=False)
.show())

我们首先计算总度数，进度数和出度数。然后我们将这些DataFrame连接在一起，使用左连接来保留没有传入或传出关系的任何节点。如果节点没有关系，则使用fillna函数将该值设置为0。
下面是在pyspark中运行代码的结果：

+-------+------+--------+---------+
|     id|degree|inDegree|outDegree|
+-------+------+--------+---------+
|   Doug|     6|       5|        1|
|  Alice|     7|       3|        4|
|Michael|     5|       2|        3|
|Bridget|     5|       2|        3|
|Charles|     2|       1|        1|
|    Amy|     1|       1|        0|
|  David|     2|       1|        1|
|   Mark|     3|       1|        2|
|  James|     1|       0|        1|

我们可以在图5-4中看到，Doug是我们Twitter图中最受欢迎的用户，有五个追随者（在链接中）。图中该部分的所有其他用户都关注他，而他只关注一个人。在真实的Twitter网络中，名人有很高的追随者数量，但往往关注很少的人。因此我们可以认为Doug是名人！

图5-4.度中心性的可视化
如果我们正在创建一个显示被最多关注的用户的页面，或者希望建议用户来跟踪，我们可以使用此算法来识别这些用户。

有些数据可能包含关系很多的非常密集的节点。这些节点不会增加太多额外的信息，并且会扭曲一些结果或增加计算复杂性。你可能希望使用子图过滤掉这些密集的节点，或者使用投影方法将关系汇总成为一个权重。