时序图神经网络总结(1)
本系列是整理关于用图神经网络(特别是图卷积)来建模时序图数据的论文。
2016-2017
- 基本概念
- 论文1 Structural Sequence Modeling with Graph Convolutional Recurrent Networks
-
- Motivation
- Method
-
- Model 1
- Model 2
- Result
- 论文2 Know-Evolve: Deep Temporal Reasoning for Dynamic Knowledge Graphs
-
- Motivation
- Model
- 论文3 Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting
- Motivation
- Method
-
-
- 空间特征提取——GCN
- 时间特征提取——Gated CNNs
- Spatio-temporal Convolutional Block
-
基本概念
- 关于数据类型:图的划分方式有很多,同构图和异构图,有属性的图和无属性的图,有向图和无向图,动态图和静态图……比如在交通预测问题中,交通网络结构固定不变,节点均表示传感器,边均表示道路(或者说传感器之间的连接)(有属性的静态同构图);比如社交网络或推荐系统等现实世界中的关系网络,随着时间而动态变换(有属性的动态异构图);而关于是有向还是无向,就视具体情况来看了。
- 图神经网络简述:从图神经网络到图卷积神经网络讲的很详细,另外,如果只想了解图卷积的知识,也可以参考这篇。关于图卷积,总体分为谱域和空域:谱域卷积是基于图信号领域的卷积定理发展来的,它要求数据是无向静态同构图(因为需要拉普拉斯算子是对称矩阵);而空域卷积则对数据的要求有放松,目前主流的方法GAT、GraphSAGE等基本上只要求是静态同构图即可。这些经典图神经网络模型并不适用于异构图,因而异构图需要更复杂的处理,常见的方法是大概是将异构图划分成多个同构图或者基于meta-path的方法。
- 关于时序建模:这方面论文确实比较多,本人才疏学浅没看得很深,但从大部分时序图神经网络模型中可以看出,RNN以及RNN的变体(LSTM和GRU)、TCN、CNN、Transformer常被用于处理时序数据。
论文1 Structural Sequence Modeling with Graph Convolutional Recurrent Networks
这篇文章发表于ICLR 2017,是比较早的一篇对结构数据进行序列学习的文章。
Motivation
目前很多研究将CNN和RNN融合来用于时空序列建模,但这些方法仅能用于欧式数据。
Method
本文提出了GCRN(Graph Convolutional Recurrent Network),将经典的RNN(Recurrent Neural Network)泛化到到结构化的数据处理。这篇文章的目的是多步预测,作者称为序列建模:
x ^ t + 1 , … , x ^ t + K = arg max x t + 1 , … , x t + K P ( x t + 1 , … , x t + K ∣ x t − J + 1 , … , x t ) \hat{x}_{t+1}, \ldots, \hat{x}_{t+K}=\arg \max _{x_{t+1}, \ldots, x_{t+K}} P\left(x_{t+1}, \ldots, x_{t+K} \mid x_{t-J+1}, \ldots, x_{t}\right) x^t+1,…,x^t+K=argxt+1,…,xt+KmaxP(xt+1,…,xt+K∣xt−J+1,…,xt)针对的数据是图结构不发生改变的无向带权同构图序列。
作者提出了两种GCRN结构,一是对每个序列先进行图卷积处理再将卷积之后的结果输入LSTM;二是将FC-LSTM中的2D卷积替换成图卷积。
Model 1
x t C N N = C N N G ( x t ) i = σ ( W x i x t C N N + W h i h t − 1 + w c i ⊙ c t − 1 + b i ) f = σ ( W x f x t C N N + W h f h t − 1 + w c f ⊙ c t − 1 + b f ) c t = f t ⊙ c t − 1 + i t ⊙ tanh ( W x c x t C N N + W h c h t − 1 + b c ) o = σ ( W x o x t C N N + W h o h t − 1 + w c o ⊙ c t + b o ) h t = o ⊙ tanh ( c t ) \begin{aligned} x_{t}^{\mathrm{CNN}} &=\mathrm{CNN}_{\mathcal{G}}\left(x_{t}\right) \\ i &=\sigma\left(W_{x i} x_{t}^{\mathrm{CNN}}+W_{h i} h_{t-1}+w_{c i} \odot c_{t-1}+b_{i}\right) \\ f &=\sigma\left(W_{x f} x_{t}^{\mathrm{CNN}}+W_{h f} h_{t-1}+w_{c f} \odot c_{t-1}+b_{f}\right) \\ c_{t} &=f_{t} \odot c_{t-1}+i_{t} \odot \tanh \left(W_{x c} x_{t}^{\mathrm{CNN}}+W_{h c} h_{t-1}+b_{c}\right) \\ o &=\sigma\left(W_{x o} x_{t}^{\mathrm{CNN}}+W_{h o} h_{t-1}+w_{c o} \odot c_{t}+b_{o}\right) \\ h_{t} &=o \odot \tanh \left(c_{t}\right) \end{aligned} xtCNNifctoht=CNNG(xt)=σ(WxixtCNN+Whiht−1+wci⊙ct−1+bi)=σ(WxfxtCNN+Whfht−1+wcf⊙ct−1+bf)=ft⊙ct−1+it⊙tanh(WxcxtCNN+Whcht−1+bc)=σ(WxoxtCNN+Whoht−1+wco⊙ct+bo)=o⊙tanh(ct)
Model 2
i = σ ( W x i ∗ G x t + W h i ∗ G h t − 1 + w c i ⊙ c t − 1 + b i ) f = σ ( W x f ∗ G x t + W h f ∗ G h t − 1 + w c f ⊙ c t − 1 + b f ) c t = f t ⊙ c t − 1 + i t ⊙ tanh ( W x c ∗ G x t + W h c ∗ G h t − 1 + b c ) o = σ ( W x o ∗ G x t + W h o ∗ G h t − 1 + w c o ⊙ c t + b o ) h t = o ⊙ tanh ( c t ) \begin{aligned} i &=\sigma\left(W_{x i} *_{\mathcal{G}} x_{t}+W_{h i} *_{\mathcal{G}} h_{t-1}+w_{c i} \odot c_{t-1}+b_{i}\right) \\ f &=\sigma\left(W_{x f} *_{\mathcal{G}} x_{t}+W_{h f} *_{\mathcal{G}} h_{t-1}+w_{c f} \odot c_{t-1}+b_{f}\right) \\ c_{t} &=f_{t} \odot c_{t-1}+i_{t} \odot \tanh \left(W_{x c} *_{\mathcal{G}} x_{t}+W_{h c} *_{\mathcal{G}} h_{t-1}+b_{c}\right) \\ o &=\sigma\left(W_{x o} *_{\mathcal{G}} x_{t}+W_{h o} *_{\mathcal{G}} h_{t-1}+w_{c o} \odot c_{t}+b_{o}\right) \\ h_{t} &=o \odot \tanh \left(c_{t}\right) \end{aligned} ifctoht=σ(Wxi∗Gxt+Whi∗Ght−1+wci⊙ct−1+bi)=σ(Wxf∗Gxt+Whf∗Ght−1+wcf⊙ct−1+bf)=ft⊙ct−1+it⊙tanh(Wxc∗Gxt+Whc∗Ght−1+bc)=σ(Wxo∗Gxt+Who∗Ght−1+wco⊙ct+bo)=o⊙tanh(ct)
这两个模型框架不一定局限于LSTM,同样可以应用到任何循环神经网络如GRU。
Result
作者将这两个模型分别应用于预测任务(moving-MNIST dataset)和自然语言建模,并且得出结果Model1的效果比Model2的效果好,原因作者认为可能是Model2中快速增长的维度,隐藏层的维度从200增加到10000。
作者进行的实验都是将欧式数据(如图像、文本)转换为图结构的数据,这样的转换本身就存在信息丢失吧(本人观点)。
论文2 Know-Evolve: Deep Temporal Reasoning for Dynamic Knowledge Graphs
这篇文章发表于ICML 2017,它主要是为了解决动态变化的知识图谱的表示学习。提出了点过程(point process)的概念,虽然好像和图卷积没有什么关系,但该作者后续在ICLR 2019又发表了一篇基于点过程的动态图学习模型。
Motivation
传统的知识图谱都被认为是静态图,但现在的数据呈现出复杂的时间动态,因而传统的知识图谱应该被增强为时序知识图谱(TKG)。
Model
本模型针对的数据是图结构发生改变的有向带权异构图序列。
作者认为,时间点过程可以看成是一个计数过程 N ( t ) N(t) N(t),表示在 t t t时刻前事件发生的次数。描述时间点过程可以用密度函数 λ ( t ) \lambda(t) λ(t),表示在之前的事件发生的条件下,当前时刻发生事件的可能性。作者将事件的发生就用密度函数来进行建模。
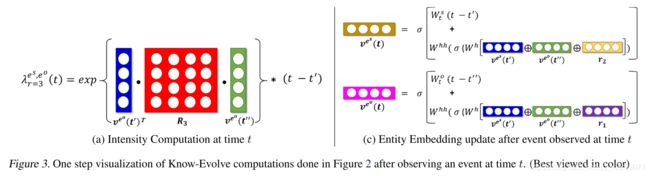
TKG的一次事件被记为 ( e s , r , e o , t ) (e^s,r,e^o,t) (es,r,eo,t),该四元组表示在 t t t时刻主体节点 e s e^s es和客体节点 e o e^o eo之间创建了一个类型为 r r r的边连接。事件按时间排序构成一个观察事件集 D D D。
对于一次事件,其密度函数计算为:
λ r e s , e o ( t ∣ t ‾ ) = f ( g r e s , e o ( t ‾ ) ) ∗ ( t − t ‾ ) \lambda^{e^s,e^o}_r(t|\overline t)=f(g_r^{e^s,e^o}(\overline t))*(t-\overline t) λres,eo(t∣t)=f(gres,eo(t))∗(t−t)其中,
g r e s , e o ( t ) = v e s ( t − ) T ⋅ R r ⋅ v e o ( t − ) g_r^{e^s,e^o}(t)=v^{e^s}(t-)^T·R_r·v^{e^o}(t-) gres,eo(t)=ves(t−)T⋅Rr⋅veo(t−)
g g g函数是用于计算主体节点和客体节点之间的相对兼容性,作为评分函数, v e s v^{e^s} ves表示节点的嵌入。 λ r e s , e o ( t ∣ t ‾ ) \lambda^{e^s,e^o}_r(t|\overline t) λres,eo(t∣t)表示在主体或客体在 t ‾ \overline t t时刻发生事件的条件下,本次事件 ( e s , r , e o , t ) (e^s,r,e^o,t) (es,r,eo,t)发生的强度。
主体嵌入更新:
v e s ( t p ) = σ ( W t s ( t p − t p − 1 ) + W h h ⋅ h e s ( t p − ) ) h e s ( t p − ) = σ ( W h ⋅ [ v e s ( t p − 1 ) ⊕ v e o ( t p − ) ⊕ r p − 1 e s ] ) v^{e^s}(t_p)=\sigma(W^s_t(t_p-t_{p-1})+W^{hh}·h^{e^s}(t_p-))\\ h^{e^s}(t_p-)=\sigma(W^h·[v^{e^s}(t_{p-1})\oplus v^{e^o}(t_p-)\oplus r^{e^s}_{p-1}]) ves(tp)=σ(Wts(tp−tp−1)+Whh⋅hes(tp−))hes(tp−)=σ(Wh⋅[ves(tp−1)⊕veo(tp−)⊕rp−1es])客体嵌入更新:
v e o ( t q ) = σ ( W t s ( t q − t q − 1 ) + W h h ⋅ h e o ( t q − ) ) h e o ( t q − ) = σ ( W h ⋅ [ v e o ( t q − 1 ) ⊕ v e o ( t q − ) ⊕ r q − 1 e o ] ) v^{e^o}(t_q)=\sigma(W^s_t(t_q-t_{q-1})+W^{hh}·h^{e^o}(t_q-))\\ h^{e^o}(t_q-)=\sigma(W^h·[v^{e^o}(t_{q-1})\oplus v^{e^o}(t_q-)\oplus r^{e^o}_{q-1}]) veo(tq)=σ(Wts(tq−tq−1)+Whh⋅heo(tq−))heo(tq−)=σ(Wh⋅[veo(tq−1)⊕veo(tq−)⊕rq−1eo])
注:这里面有多个时间表示需要区分, t − t- t−、 t − 1 t-1 t−1、 t ‾ \overline{t} t分别表示什么?
假设 t p t_p tp是节点 e s e^s es参与的本次事件的时间(当前事件是e^s的第p个事件)
t p − 1 t_{p-1} tp−1:表示 e s e^s es参与的上一个事件的时间;
t p − t_p- tp−:表示在 t p t_p tp时刻前,最近一个时刻;
t p ‾ \overline{t_p} tp: = m a x ( t e s − , t e o − ) =max(t^{e^s}-,t^{e^o}-) =max(tes−,teo−),表示 e s e^s es或 e o e^o eo最近一次参与事件的时间。
乍一看好像强度函数并没有用来更新节点嵌入,但在损失函数中,作者通过最小化强度函数的联合负对数似然来学习模型,具体分析可以看论文。
论文3 Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting
这篇文章发表于IJCAI 2018,它将交通网络构建成无向图,然后运用谱域图卷积和卷积序列模型(convolutional sequence model)来建模。
Motivation
- 很多深度学习方法可以被用于各种交通问题,如DBN、SAE等,但这些网络都不能从输入中同时提取空间和时间特征;
- CNN被用来提取空间特征,但它只能用于欧式数据;
- 基于RNN的网络很难训练并且计算量大(RNN运行时是将序列的信息逐个处理,不能实现并行操作,导致运行速度慢)
Method
v ^ t + 1 , … , v ^ t + H = arg max v t + 1 , … , v t + B l o g P ( v t + 1 , … , v t + H ∣ v t − M + 1 , … , v t ) \hat v_{t+1},\ldots,\hat v_{t+H}=\underset{v_{t+1}, \ldots, v_{t+B}}{\arg \max } log P(v_{t+1},\ldots,v_{t+H}|v_{t-M+1},\ldots,v_t) v^t+1,…,v^t+H=vt+1,…,vt+BargmaxlogP(vt+1,…,vt+H∣vt−M+1,…,vt)
图 G = ( V t , E , W ) \mathcal{G}=(V_t,\mathcal{E},W) G=(Vt,E,W),节点表示 n n n个监控位置,边表示这些监控位置之间的连接。针对的数据是图结构不发生改变的无向带权同构图序列
空间特征提取——GCN
y j = ∑ i = 1 C i Θ i , j ( L ) x i ∈ R n , 1 ≤ j ≤ C o y_j=\sum_{i=1}^{C_i}\Theta_{i,j}(L)x_i∈R^n,1≤j≤C_o yj=i=1∑CiΘi,j(L)xi∈Rn,1≤j≤Co输入的特征是 X ∈ R n × C i X∈R^{n×C_i} X∈Rn×Ci,输出的卷积结果是 Y ∈ R n × C o Y∈R^{n×C_o} Y∈Rn×Co。输入的第 i i i个元素 x i ∈ R n x_i∈R^n xi∈Rn,也就是所有节点的第 i i i个维度特征。对于每个时间步的 V t V_t Vt的特征向量 X t X_t Xt,可以并行地进行空间信息的提取。
时间特征提取——Gated CNNs
时间卷积层包含一个宽度为 K t K_t Kt的1D卷积和gated linear units(GLU),对于图 G \mathcal{G} G中的每个节点,时间卷积会处理其 K t K_t Kt邻居,并且无padding,因而每次卷积都会缩短 K t − 1 K_t-1 Kt−1的序列长度。
1D卷积:卷积核 Γ ∈ R K t × C i × 2 C o \Gamma∈R^{K_t×C_i×2C_o} Γ∈RKt×Ci×2Co,将输入 Y ∈ R M × C i Y∈R^{M×C_i} Y∈RM×Ci(单个节点的时间序列)映射到两个向量,P、Q: [ P Q ] ∈ R ( M − K t + 1 ) × ( 2 C o ) [P{\,}Q]∈R^{(M-K_t+1)×(2C_o)} [PQ]∈R(M−Kt+1)×(2Co);
GLU:1D卷积得到的 P 、 Q ∈ R ( M − K t + 1 ) × C o P、Q∈R^{(M-K_t+1)×C_o} P、Q∈R(M−Kt+1)×Co,作为GLU的输入,进行哈达玛乘积运算:
Γ ∗ T Y = P ⊙ σ ( Q ) ∈ R ( M − K t + 1 ) × C o \Gamma *_\Tau Y=P\odot\sigma(Q)∈R^{(M-K_t+1)×C_o} Γ∗TY=P⊙σ(Q)∈R(M−Kt+1)×Co
可以将这个过程映射到所有节点上,也就是输入不再是 Y ∈ R M × C i Y∈R^{M×C_i} Y∈RM×Ci而是 Y ∈ R M × n × C i \mathcal{Y}∈R^{M×n×C_i} Y∈RM×n×Ci。
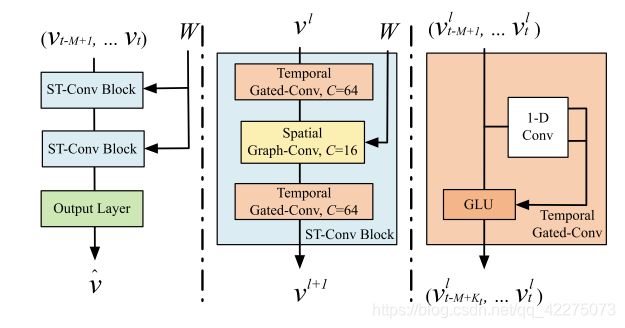
Spatio-temporal Convolutional Block
一个block就是前面图片中的三明治结构,两个时间层中间一个空间层。 v l ∈ R M × n × C l v^l∈R^{M×n×C_l} vl∈RM×n×Cl表示 l l l层的输入, v l + 1 ∈ R ( M − 2 ( K t − 1 ) ) × n × C l + 1 v^{l+1}∈R^{(M-2(K_t-1))×n×C_{l+1}} vl+1∈R(M−2(Kt−1))×n×Cl+1既是 l l l层的输出又是 l + 1 l+1 l+1层的输入:
v l + 1 = Γ 1 l ∗ τ R e L U ( Θ l ∗ G ( Γ 0 l ∗ τ v l ) ) v^{l+1}=\Gamma^l_1*_\tau ReLU(\Theta^l*_\mathcal{G}(\Gamma^l_0*_\tau v^l)) vl+1=Γ1l∗τReLU(Θl∗G(Γ0l∗τvl))
其中 Γ 0 l \Gamma^l_0 Γ0l表示block中第一个temporal层, Γ 1 l \Gamma^l_1 Γ1l表示block中的第二个temporal层。
疑惑:论文中引用了一个同期的论文Diffusion convolutional recurrent neural network: Data-driven traffic forecasting,称该模型为GCGRU,并作为baseline,而这篇论文提出的方法明明是DCRNN啊……(貌似是作者投稿的版本问题,GCGRU是第一版中命名的模型)