快速傅里叶变换——FFT

1·为什么要进行傅里叶变换

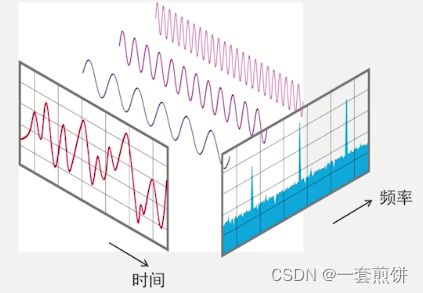
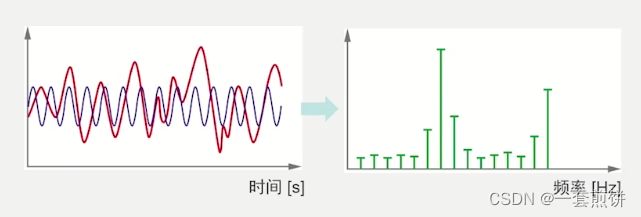
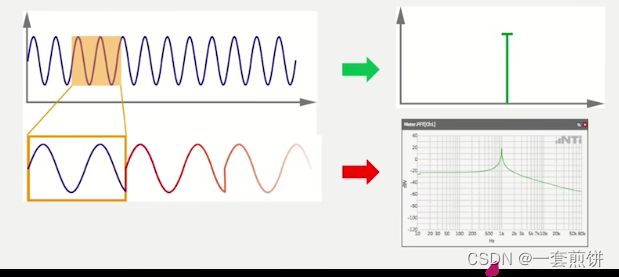
傅里叶变换——进行信号的分解过程

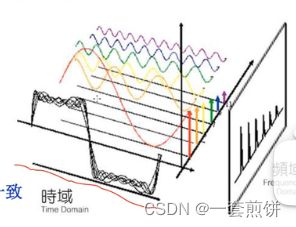
时域信号——分解成一系列频率下的正弦//余弦信号（两者在相位上有所不同），一般情况下可以统称为正弦信号。

 上图表示了傅里叶的变化过程。对于时域的信号，可以将其分解成一系列频域下的正弦信号，每个正弦信号都有各自的幅值和相位。以这些正弦信号的频率为横坐标，各个正弦信号的幅值为纵坐标。可以绘制出频率幅值图。同样的，以这些正弦信号的幅值为横坐标，相位值为纵坐标，可以绘制出频率相位图，频率幅值图和频率相位图统称为频谱图。

2.傅里叶变换的好处——正弦信号的特点

通过傅里叶变换我们将时域里 的原信号分解成了一系列频域下的正弦信号。

（1）正弦信号比原信号更加的简单。（2）对于线性系统来说，正弦信号的频率保持性。当线性系统的输入为正弦信号时，输出仍是同频率的正弦信号。输出的正弦信号的幅值和相位可能发生变化，但是频率与输入正弦信号保持一致性。频率保持性具有很高的工程使用价值。

3.傅里叶变换的离散型和周期性

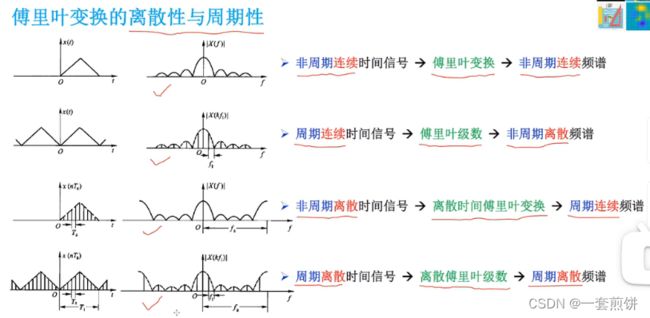
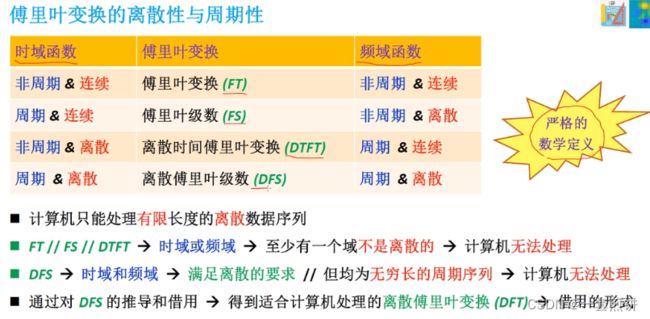
针对不同的时域信号有着不同的类型的傅里叶变换与之相对应，具体来说有以下四种情况：

 

 FFT的应用

主要用在信号分析方面，分析音频的信号，假设现在有个失真的音频信号，发现他的总斜坡失真比较高，我们此时想知道是什么原因造成这种失真的情况，通过FFT 的频谱就可以帮助我们找到失真信号。FFT还可以用于除错微调，优化。

FFT运行的基本原理或者过程，怎么把时域信号转换成频域信号的？

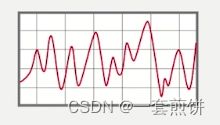
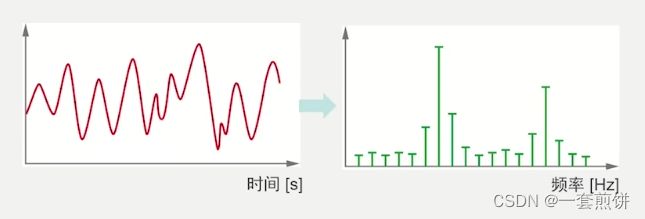
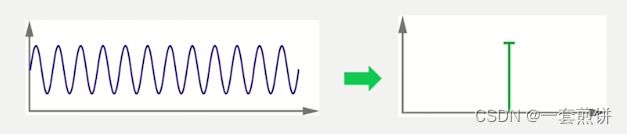
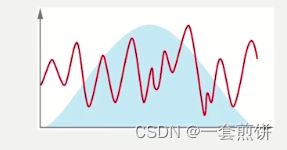
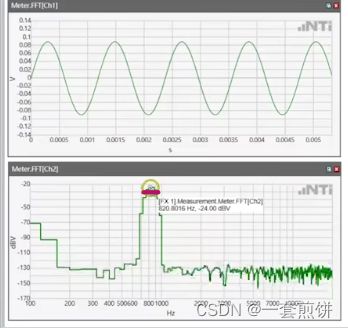
FFT计算的是周期时域信号的频谱。

上图就是一个时域信号，我们要把它分解成一个个周期性的正弦信号，每个正弦信号都有特定的幅值和频率。FFT显示的是这些频率和幅值，这样我们就把时域的信号转换成频域的信号。

 上述这个过程是怎么样进行的？

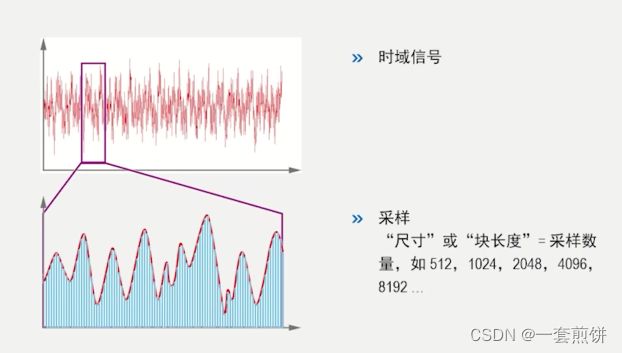
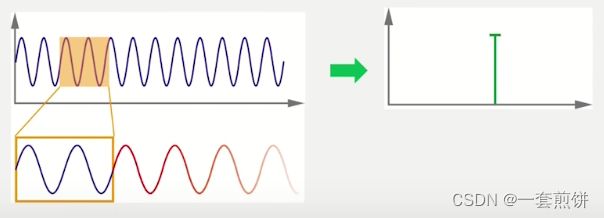
 过程：1，选取时域信号当中的某一段，采样过程。这个地方就涉及到了FFT 的第一个参数块长度（表示一个采样里采了多少个样本，块长度一般是取2的整数幂）

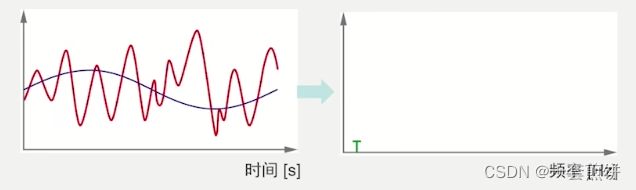
2，用一个公式来表示一下，这个公式的意义就是用来分解信号的，因为之前说FFT使用一个个正弦波来表示时域信号的，所以我们要确定正弦信号和时域信号的相关性，并且这个正弦波也要匹配块长度。所以通过这个公式来计算出正弦波和时域信号的相关性。

对应的结果放在频谱中，频谱的幅值体现的是相关性的大小。

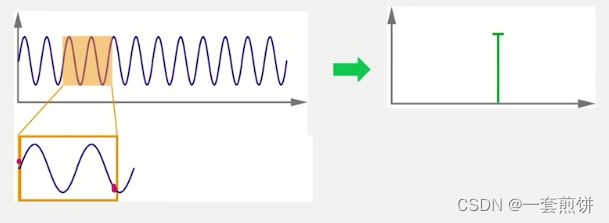
然后我们把频率翻倍在给出一个正弦波。重复这样的过程。

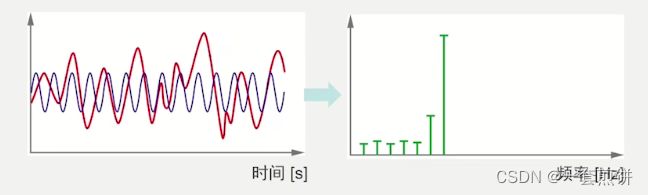
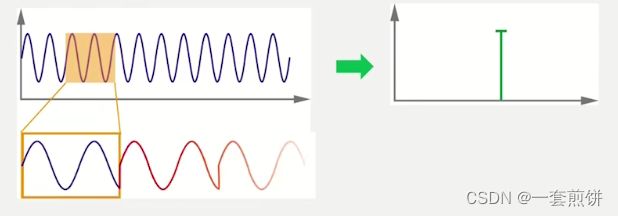
 我们可以看下面这个图当中，这个正弦波与原始信号的相关性非常高，所以在右侧的图谱中它的值非常的大。

 这样一个个频率重复就可以得到需要频段的频谱。

 

 这样就成功的分解了原始信号。

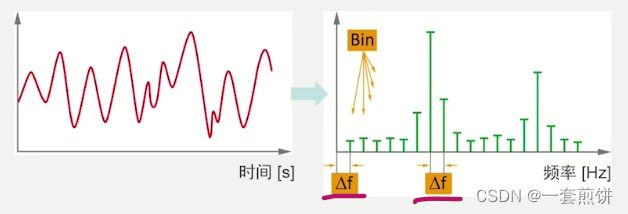
上述变换就是FFT 变换的核心过程。需要注意的是图谱的幅值单位不是变频，而被称为Bin。（这个Bin代表了相关性的大小），两个Bin之间的距离为f,这个是固定的，表示的是FFT频谱的频率分辨率。

 是不变的，除非改变FFT 的块长度。否则，频率分辨率是不变的。

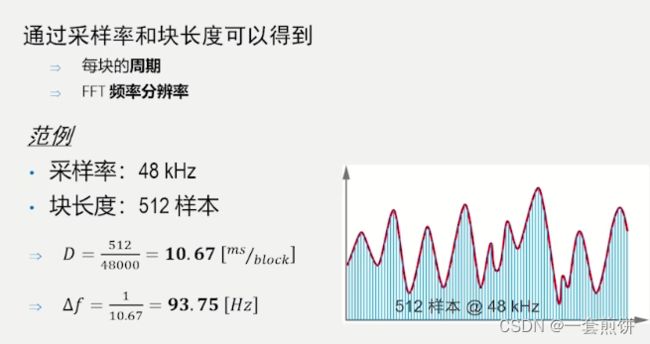
采样率和块长度都是非常重要的。其中，块长度也就是样本的数量跟FFT采集的周期有直接的关系，块长度对频率分辨率有直接的影响，假设采样的频率是48kHZ,块长度是512。计算非常的简单。

 512/48000得到每一个块的周期，而频率分辨率就是周期的倒数。很明显，块长度增加了，周期也会增大，分辨率就会变小。

另一个比较复杂的概念——弥散/泄露的含义

主要是因为周期变化的时域信号或者分量并没有完美的匹配FFT 的块

 

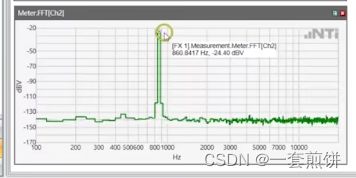
上图是一个完美的正弦波信号，右图是他的FFT频谱图。但是在显示当中，正弦波并不总是这样的完美，理想状况下，采样的窗口可以完美的覆盖一个正弦波信号，并且可以完美的过度下去。如下图所示：

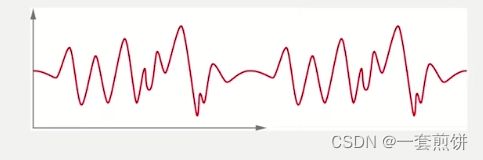
但是，实际上，时域信号并不会完美的采样到一个正弦信号，就是采样的起点和终点并不在一个幅值上，如下图：

这样的情况会导致每个块之间会发生跳变，这样的跳变会导致连续性被打破。就形成了弥散。FFT的峰值频率和激波是相同的。此时就不是一个单独的Bin，他的左右两侧还有很多的Bin 靠在一起。这样的情况并不是我们想要的。

 

为避免出现这样的情况，就出现了窗函数，他的作用就是尽量的让每一个块过度的很平滑。从而减少弥散。

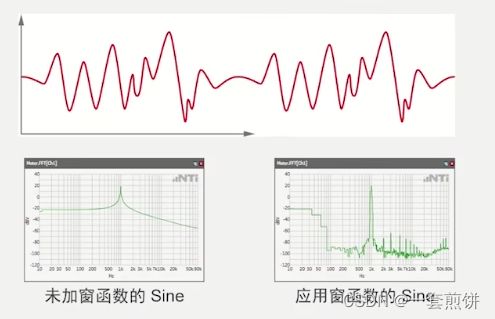
 上图是一个典型的窗函数，会随着时间的增大而缩小，对原始信号施加窗函数之后就会变成下图的形式。加上窗函数之后再首位连接时会变得比较平滑。

在使用了FFT时间窗的图谱和未使用的图谱相对比。明显的可以看到一个激波和后面失真（噪声）的一些情况在。

上面的这个图就是加上传函数之后出现的FFT频谱图，但是可以看到激波的Bin比较宽，出现这个线性的原因是因为和快长度有关，如果提高块长度，那么分辨率就会变高，那么就会出现一个比较窄的Bin。

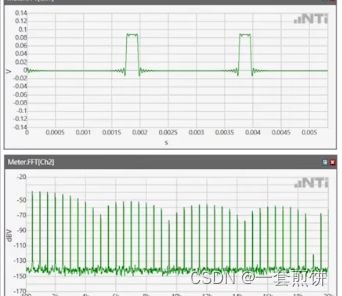
 FFT分析脉冲信号

在时域里面，脉冲信号是由不同频率的正弦波组成的，在FFT里面有不同成分的斜坡叠加起来。

 

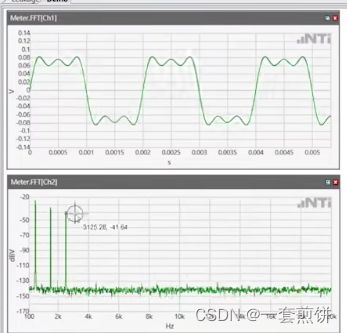
 FFT分析方波

在是与里面是由正弦波的信号来表示的。当叠加一些成分进去的时候，正弦波信号会发生变化。

 

 方波是由激波信号（500HZ），三次谐波（1500HZ，幅值是激波的三分之一），五次谐波（是激波的五分之一），，，，增加的奇次谐波越多，就越接近于方波。

FFT分析分噪声，不是稳定信号，在测试的时候会有一些突变，此时们就需要一个平均的模式，点完平均模式之后这个噪声就会平稳许多。