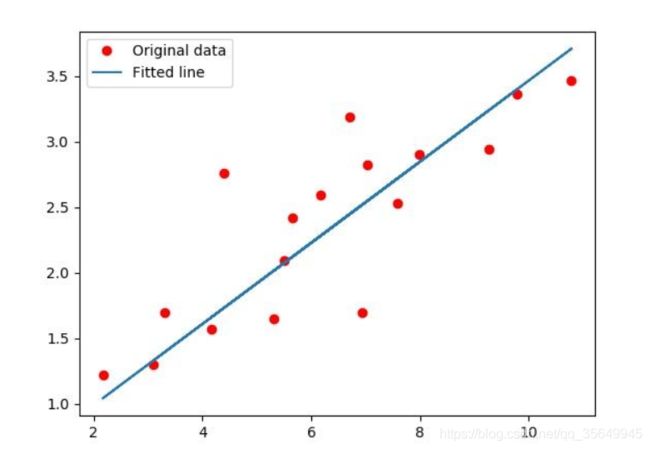
线性模型(linear model)
基本形式
y = a x + b y=ax +b y=ax+b
线性模型顾名思义,模型拟合的函数是线性的,我们从小学就学过的线性函数如上上式所示,其中 a a a表示参数, x x x表示未知数, b b b表示常量;在机器学习中假设一个模型是上面这样的函数,则 x x x表示样本值,而机器学习简单来说就是通过所给的样本值来拟合这样一条曲线,即通过实际的 ( x i , y i ) (x_i,y_i) (xi,yi)来求得 a 和 b a和b a和b的过程。(当然这只是建立模型的第一步,这里先不讲)
接下来看一个稍微复杂一点的函数:
y = a x 1 + b x 2 + c x 3 + d x 4 + C y=ax_1+bx_2+cx_3+dx_4+C y=ax1+bx2+cx3+dx4+C
上式与第一个式子相比只是多了几个未知数,这些未知数表示一个样本的多个属性。在机器学习中,例如:通过建立模型预测某地的房价 y y y,我们都知道一个地方的房价受多种因素的影响,比如面积、地段、交通等,这些就是上式中的 x i x_i xi,同时也称为属性。
一般地,上式可以写成向量的形式(这里用到了向量乘法的简单知识), w T ⃗ \vec{w^T} wT表示列向量的转置:
f ( x ) = y = w T ⃗ x ⃗ + C = ( a b c d ) T ∗ ( x 1 x 2 x 3 x 4 ) + C f(x)=y=\vec{w^T}\vec{x}+C ={\begin{pmatrix} a\\b\\c\\d \end{pmatrix}\quad }^T * {\begin{pmatrix} x_1\\x_2\\x_3\\x_4 \end{pmatrix}\quad }+C f(x)=y=wTx+C=⎝⎜⎜⎛abcd⎠⎟⎟⎞T∗⎝⎜⎜⎛x1x2x3x4⎠⎟⎟⎞+C
其中 w ⃗ = ( a b c d ) T \vec{w}={\begin{pmatrix} a\\b\\c\\d \end{pmatrix}\quad }^T w=⎝⎜⎜⎛abcd⎠⎟⎟⎞T表达了各个属性在预测中的重要性(比重)。
线性回归(linear regression)
回归问题指的是自变量与因变量的关系是连续值,比如房价受面积的影响是连续的;而预测抛掷硬币正反面时,结果只用正面和反面(当然可能存在立着的情况),假设正面为1,反面为0,不存在中间值,则这是一个二分类(classification)问题,若属性值间存在“序”的关系,可以转变为回归问题,例如一个好瓜熟度为1,不熟为0,则不好不坏可设为0.5。
线性回归通过给定测试集 D { ( x 1 ⃗ , y 1 ) , ( x 2 ⃗ , y 2 ) , ( x 3 ⃗ , y 3 ) . . . } 这 里 x i ⃗ = ( x i 1 , x i 2 , x i 3 , x i 4 . . . ) 表 示 一 个 属 性 集 , ( 下 标 表 示 的 i 个 样 本 , 上 标 表 示 一 个 样 本 的 第 i 个 属 性 , y i 表 示 样 本 的 真 实 值 ) D\{(\vec{x_1},y_1),(\vec{x_2},y_2),(\vec{x_3},y_3)...\} \\这里\vec{x_i}=(x_i^1,x_i^2,x_i^3,x_i^4...)表示一个属性集,(下标表示的i个样本,上标表示一个样本的第i个属性,y_i表示样本的真实值) D{(x1,y1),(x2,y2),(x3,y3)...}这里xi=(xi1,xi2,xi3,xi4...)表示一个属性集,(下标表示的i个样本,上标表示一个样本的第i个属性,yi表示样本的真实值)
下面是得到一个简单线性模型(假设模型只有一个属性值)的例子:
- Step1 Model
假设房价y只受面积x的影响,则可设模型 f ( x i ) = w x + b f(x_i)=wx+b f(xi)=wx+b
给某地训练集样本值 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) . . . ( x i , y i ) . . . } D=\{(x_1,y_1),(x_2,y_2)...(x_i,y_i)...\} D={(x1,y1),(x2,y2)...(xi,yi)...},我们需要用给定的训练值求出 w , b w,b w,b。但我们根据模型预测出的结果与实际值会有一些差别。(有同学会有疑问,既然有真实值为什么还要预测,在这里我们是通过已有的样本值来训练出一个模型,以便能通过模型预测更多的值,使模型得以泛化,因此我们训练的模型误差越小越好。但同时应避免过拟合问题)
- Step2 Goodness of Function
为了衡量一个模型函数的好坏,需要设置一个损失函数来表示预测值与实际值的差距
即: E ( f ) = ∑ i = 1 n ( f ( x i ) − y i ) 2 = ∑ i = 1 n ( w x i + b − y i ) 2 E(f)=\sum_{i=1}^{n}(f(x_i)-y_i)^2=\sum_{i=1}^{n}(wx_i+b-y_i)^2 E(f)=i=1∑n(f(xi)−yi)2=i=1∑n(wxi+b−yi)2
其中 ( f ( x i ) − y i ) 2 (f(x_i)-y_i)^2 (f(xi)−yi)2表示均方误差, f ( x ) f(x) f(x)是由模型得出的预测值,通常我们要获得使均方误差,即损失函数 L ( f ) 最 小 化 L(f)最小化 L(f)最小化时的w和b,此时的模型是相对较好的。
即:
( w ∗ , b ∗ ) = a r g min ( w , b ) ( E ( w , b ) ) = a r g min ( w , b ) ∑ i = 1 n ( w x i + b − y i ) 2 (w^*,b*)=arg \min_{(w,b)}(E(w,b))=arg \min_{(w,b)}\sum_{i=1}^{n}(wx_i+b-y_i)^2 (w∗,b∗)=arg(w,b)min(E(w,b))=arg(w,b)mini=1∑n(wxi+b−yi)2
a r g min arg \min argmin表示使函数 E ( w , b ) E(w,b) E(w,b)的值最小时的 w , b w,b w,b的值。 - Step3 Best Function
均方误差对应了几何上常用的欧基里得距离(欧式距离),基于均方误差最小化来进行模型求解的方法称为最小二乘法,要找到拟合最好的模型,就要找到使函数 E ( w , b ) E(w,b) E(w,b)的值最小时的 w , b w,b w,b的值。
求解 w w w和 b b b使 E ( w , b ) = ∑ i = 1 n ( y i − w x i − b ) 2 E(w,b)=\sum_{i=1}^{n}(y_i-wx_i-b)^2 E(w,b)=∑i=1n(yi−wxi−b)2最小化的过程,称为线性回归模型的最小二乘的“参数估计”,先不管它叫什么,这里可以把 E ( f ) E(f) E(f)看做是关于 w 和 b w和b w和b的函数,求最小化的过程可以用求偏导的方式。
对w和b求偏导:
∂ E ( w , b ) ∂ w = 2 ( w ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − b ) x i ) ∂ E ( w , b ) ∂ b = 2 ( m b − ∑ i = 1 m ( y i − w x i ) ) \begin{aligned} \frac{\partial E_{(w, b)}}{\partial w} &=2\left(w \sum_{i=1}^{m} x_{i}^{2}-\sum_{i=1}^{m}\left(y_{i}-b\right) x_{i}\right) \\ \frac{\partial E_{(w, b)}}{\partial b} &=2\left(m b-\sum_{i=1}^{m}\left(y_{i}-w x_{i}\right)\right) \end{aligned} ∂w∂E(w,b)∂b∂E(w,b)=2(wi=1∑mxi2−i=1∑m(yi−b)xi)=2(mb−i=1∑m(yi−wxi))
令上面两式为0,可得:
0 = w ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − b ) x i w ∑ i = 1 m x i 2 = ∑ i = 1 m y i x i − ∑ i = 1 m b x i \begin{array}{c}{0=w \sum_{i=1}^{m} x_{i}^{2}-\sum_{i=1}^{m}\left(y_{i}-b\right) x_{i}} \\\\\ {w \sum_{i=1}^{m} x_{i}^{2}=\sum_{i=1}^{m} y_{i} x_{i}-\sum_{i=1}^{m} b x_{i}}\end{array} 0=w∑i=1mxi2−∑i=1m(yi−b)xi w∑i=1mxi2=∑i=1myixi−∑i=1mbxi
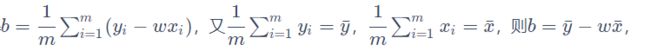
将 b b b代入含 w w w的式子中:

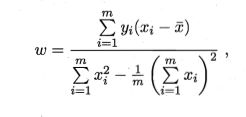
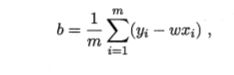
其中 x ‾ = 1 / m ∑ i = 1 n x i \overline{x}=1/m\sum_{i=1}^nx_i x=1/mi=1∑nxi这样,一个简单的线性模型就得到了。
多元线性回归
多数情况不会像上述模型那么简单,就像房价不会仅受面积的影响,需要考虑离市区的距离,离地铁站的距离,朝向等,,,会有多个属性值共同影响最后的结果,因此多元的情况我们常需要将线性模型设置为下面的形式:
f ( x ) = y = w T ⃗ x ⃗ + C = ( a b c d ) T ∗ ( x 1 x 2 x 3 x 4 ) + C f(x)=y=\vec{w^T}\vec{x}+C ={\begin{pmatrix} a\\b\\c\\d \end{pmatrix}\quad }^T * {\begin{pmatrix} x_1\\x_2\\x_3\\x_4 \end{pmatrix}\quad }+C f(x)=y=wTx+C=⎝⎜⎜⎛abcd⎠⎟⎟⎞T∗⎝⎜⎜⎛x1x2x3x4⎠⎟⎟⎞+C
假设训练集里有m个样本,每个样本有d个属性值。
则:
D = { x 11 x 12 . . . x 1 d x 21 x 22 . . . x 2 d x 31 x 32 . . . x 3 d . . . . . . . . . . . . x m 1 x m 2 . . . x m d } D=\begin{Bmatrix} x_{11} & x_{12}&...&x_{1d} \\ x_{21} & x_{22}&...&x_{2d}\\ x_{31} & x_{32}&...&x_{3d} \\...&...&...&...\\ x_{m1} & x_{m2}&...&x_{md}\end{Bmatrix}\quad D=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x11x21x31...xm1x12x22x32...xm2...............x1dx2dx3d...xmd⎭⎪⎪⎪⎪⎬⎪⎪⎪⎪⎫
其中每一行,即 ( x 11 x 12 . . . x 1 d ) \begin{pmatrix} x_{11} & x_{12}&...&x_{1d}\end{pmatrix} (x11x12...x1d)表示一个样本值,每竖行表示某个样本对应属性的值。
由此可得方程组:
y 1 = w 1 ∗ x 11 + w 2 ∗ x 12 + . . . + w d ∗ x 1 d + b y 2 = w 1 ∗ x 21 + w 2 ∗ x 22 + . . . + w d ∗ x 2 d + b . . . y m = w 1 ∗ x m 1 + w 2 ∗ x m 2 + . . . + w d ∗ x m d + b y_1=w_1*x_{11}+w_2*x_{12}+...+w_d*x_{1d}+b\\ y_2=w_1*x_{21}+w_2*x_{22}+...+w_d*x_{2d}+b\\ ...\\ y_m=w_1*x_{m1}+w_2*x_{m2}+...+w_d*x_{md}+b y1=w1∗x11+w2∗x12+...+wd∗x1d+by2=w1∗x21+w2∗x22+...+wd∗x2d+b...ym=w1∗xm1+w2∗xm2+...+wd∗xmd+b
由上面的方程组就可以求得 w ⃗ = ( w 1 , w 2 , . . . w d ) \vec{w}=(w_1,w_2,...w_d) w=(w1,w2,...wd)以及b的预测值了
由线性代数的知识可以将上述方程组转化为矩阵相乘的形式:
y ^ = [ y 1 y 2 . . . y d ] = [ x 11 x 12 . . . x 1 d 1 x 21 x 22 . . . x 2 d 1 x 31 x 32 . . . x 3 d 1 . . . . . . . . . . . . . . . x m 1 x m 2 . . . x m d 1 ] ∗ [ w 1 w 2 . . . w d b ] = [ x 1 T 1 x 2 T 1 . . . . . . x m T 1 ] ∗ [ w ⃗ b ] T = X w ^ \hat{y}=\begin{bmatrix} y_{1} \\y_{2}\\...\\y_{d}\end{bmatrix}=\begin{bmatrix} x_{11} & x_{12}&...&x_{1d}&1\\ x_{21} & x_{22}&...&x_{2d}&1\\ x_{31} & x_{32}&...&x_{3d} &1\\...&...&...&...&...\\ x_{m1} & x_{m2}&...&x_{md}&1\end{bmatrix}*\begin{bmatrix} w_{1} \\w_{2}\\...\\w_{d}\\b\end{bmatrix}=\begin{bmatrix} x_{1}^T&1 \\x_{2}^T&1\\...&...\\x_{m}^T&1\end{bmatrix}*\begin{bmatrix} \vec{w}&b\end{bmatrix}^T=X\hat{w} y^=⎣⎢⎢⎡y1y2...yd⎦⎥⎥⎤=⎣⎢⎢⎢⎢⎡x11x21x31...xm1x12x22x32...xm2...............x1dx2dx3d...xmd111...1⎦⎥⎥⎥⎥⎤∗⎣⎢⎢⎢⎢⎡w1w2...wdb⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎡x1Tx2T...xmT11...1⎦⎥⎥⎤∗[wb]T=Xw^
其中 y ⃗ = [ y 1 y 2 . . . y d ] \vec{y}=\begin{bmatrix} y_{1} \\y_{2}\\...\\y_{d}\end{bmatrix} y=⎣⎢⎢⎡y1y2...yd⎦⎥⎥⎤, X = [ x 1 T 1 x 2 T 1 . . . . . . x m T 1 ] X=\begin{bmatrix} x_{1}^T&1 \\x_{2}^T&1\\...&...\\x_{m}^T&1\end{bmatrix} X=⎣⎢⎢⎡x1Tx2T...xmT11...1⎦⎥⎥⎤, w ^ = [ w ⃗ b ] T \hat{w}=\begin{bmatrix} \vec{w}&b\end{bmatrix}^T w^=[wb]T
类比一元的情况,矩阵应该用其转置乘其本身,( y ⃗ \vec{y} y是样本的真实值)即求:
![]()
令:
![]()
对 w ^ \hat{w} w^求导(涉及矩阵求导知识):
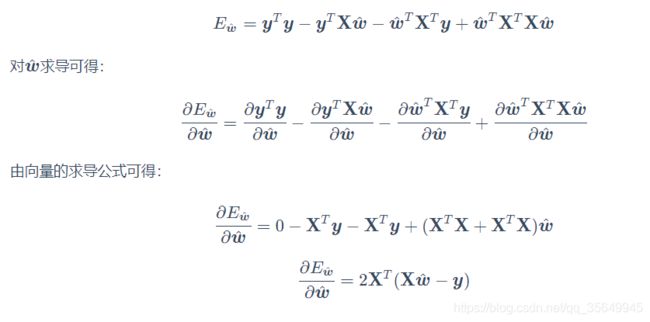
令上式为0可求得解。