01背包问题三种解决（贪心动态规划分支限界）

一、实验目的

1、深入理解背包相关问题。

2、能正确设计相应的算法，解决实际问题。

  3、掌握算法时间复杂度分析。

二、实验要求

1. 用3种方法求解0-1背包问题（贪心算法、动态规划、分支限界法），获得精确最优解或近似最优解均可。
2. 通过一个规模较大的实例比较不同方法的求解速度，分析不同算法的时间复杂度，并分析是否能获得最优解。
3. 实验结果跟实验设置的参数（如：背包容量、物品的体积）关系很大，简要分析参数对结果的影响。

三、实验原理

1.动态规划解0-1背包原理：

动态规划基本思想是将带求解的问题分解成若干子问题，先求解子问题，再结合这些子问题的解得到原问题的解。

用动态规划算法解0-1背包原理为：设0-1背包问题的子问题

max∑vkxk,(k=i-n)     ∑wkxk<=j

                      xk∈{0,1}  i<=k<=n

的最优值为m(i,j),即m(i,j)是背包容量为j,可选择物品为i,i+1,···，n时0-1背包问题的最优值，由0-1背包问题的最优子结构性质，可以建立计算m(i,j)的递归式如下：

m(i,j)=     max{m(i+1,j),m(i+1,j-wi+vi)}  j>=wi

          m(i+1,j)     0<=j<=wn

m(n,j)=    vn  j>=wn

1. 0<=j

所以基于以上讨论，当wi(1<=i<=n)为正整数时，用二维数组m[][]来存储m(i,j)的值，最后m[1][c]给出所要求的0-1背包的最优值，相应的最优解有Traceback函数计算如下：如果m[1][c]=m[2][c],则x1=0,否则x1=1。当x1=0时，由m[2][c]继续构造最优解。当x1=1时，由m[2][c-w1]继续构造最优解。以此类推，可构造出相应的最优解（x1,x2,···xn）。

2.贪心算法解0-1背包原理

贪心算法是一种只考虑当前最优的算法，其不从总体上考虑，所以贪心算法不是对所有问题都能求得整体最优解，像本实验中的0-1背包问题，用贪心算法一般求得的是局部最优解，用贪心算法解0-1背包问题原理如下：

首先我们按照物品的单位重量价值来进行排序，然后按照单位重量价值从高到低依次进行选择，若其能装入背包则将其装入，不能则继续判断下一个直至所有物品都判断完，就得到了问题的一个解。但是对于0-1背包问题，用贪心算法并不能保证最终可以将背包装满，部分剩余的空间使得单位重量背包空间的价值降低了，这也是用贪心算法一般无法求得0-1背包最优解的原因。

3.分支限界发解0-1背包问题原理

本次实验中用优先队列式分支限界法求解0-1背包问题，原理如下：（1）分支限界法通常是用广度优先或最大效益优先方式搜索问题的解空间树，而对于本次实验中求解的0-1背包问题的解空间树是一颗子集树；（2）在分支限界法中还有一个活结点表，活结点表中的每个活结点只有一次机会成为扩展结点，一旦成为扩展结点就一次性产生其所有儿子结点，在这些儿子结点中，导致不可行解或导致非最优解的儿子结点被舍弃，其余的儿子结点则被加入到活结点中表。而对于0-1背包问题中的每个活结点只有两个儿子结点，分别表示对该物品选取或舍去；对于一个儿子结点是否能加入到活结点表中有两个条件用于判断，一个是约束函数判断能否满足背包容量约束，另一个是限界函数判断是否可能得到最优解。（3）为了能够比较快速的找到0-1背包问题的解，每次选取下一个活结点成为扩展结点的判断依据是当前情况下最有可能找到最优解的下一个结点。所以每次选择扩展结点采取如下方法：当前情况下，在活结点表中选择活结点的上界uprofit(通过限界函数Bound求出)最大的活结点成为当前的扩展结点。这一过程一直持续到找到所需的解或活结点表为空时为止。此过程体现出分支限界法以“最大效益优先”方式进行。（4）为了在活结点表中选择拥有最大的上界uprofit的活结点，在活结点表上实现优先队列。

（5）通过上述第3点，可以求出0-1背包问题的最优值。为了求出0-1背包问题的最优解，对于每一个在 活结点表中的活结点创建一个树结点，树节点需要反映该结点的父节点和是否有左孩子（有左孩子 表示物品i选取了，没有左孩子表示物品i舍去了）。因此，可以构造一颗子集树，最优解就是从树根 到叶子结点的路径，子集树的第i层的所有结点就是在不同情况下对物品i的取舍结点。构造最优解的 顺序是从叶子结点到根结点的过程。

4.三种方法求解速度的比较

三种方法的求解速度w我们可以通过比较三种方法的求解所需时间来实现，而求解所需要的时间在C++中也较为容易实现，通过cout << "The run time is:" << (double)clock() /CLOCKS_PER_SEC<< "s" << endl;这句语句即可获得所需时间。

四、实验结果

1.首先，先对一简单的实例，用三种方法进行求解，该简单实例是在物品种类n=5,背包容量c=10,价值数组为v={6,3,5,4,6};重量数组w={2,2,6,5,4};

从上面三个结果的截图我们可以发现对于数据比较少的简单的案例三种方法所用时间基本相差不大，并且因为所选案例关系，三种方法都求得了最优解，下面换一个数据少的案例，来体现贪心算法不一定能求得最优解的性质：n=4,背包容量c=15,价值数组为v={5 6 7 9};重量数组w={2 3 5 7};

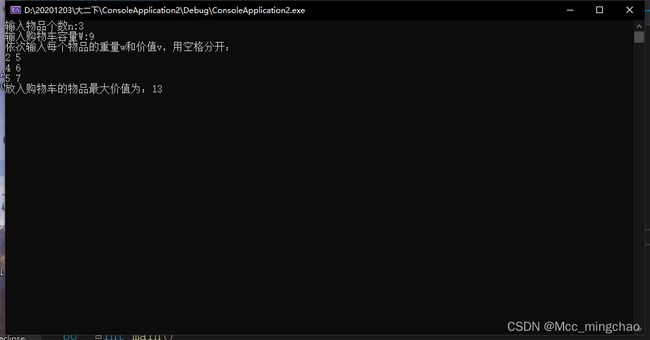
动态规划算法结果：

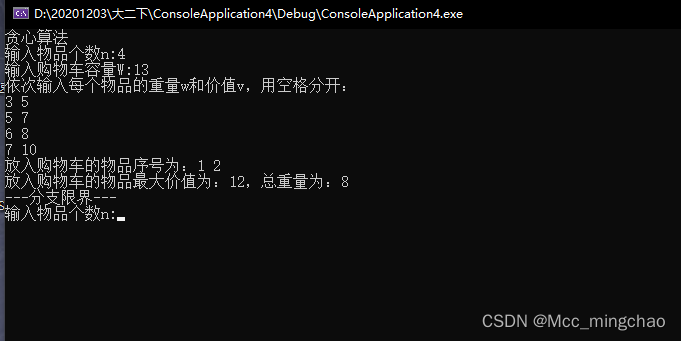
贪心算法结果：

（输入见图）

分支限界结果：

（输入见图）

2.对大数据求解

下面用一组较大规模的数据，来进行求解：

这组实例设置如下：int n=50; int c=100;

int v[50]={3,5,4,5,6,3,4,7,6,2,3,5,6,7,8,9,7,10,3,4,5,1,2,6,7,9,5,6,7,9,6,4,3,2,3,5,6,7,8,6,4,2,1,3,4,6,7,8,9,2};

int w[50]={6,5,4,3,5,6,7,4,6,7,7,8,4,3,4,5,6,8,3,4,2,5,6,7,8,5,6,4,3,3,5,6,8,9,4,2,5,6,7,8,9,3,2,4,6,7,8,9,9,6};

下面是用三种算法求解的结果截图：

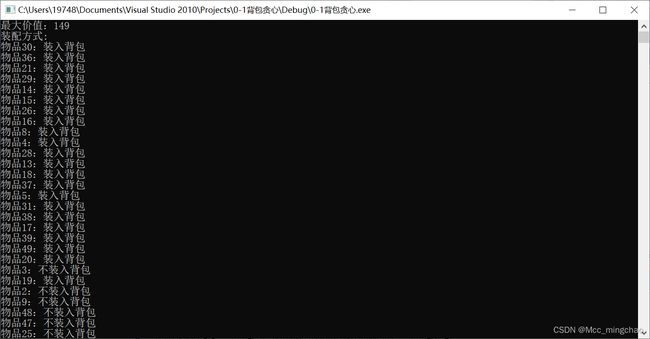
动态规划：

贪心算法：

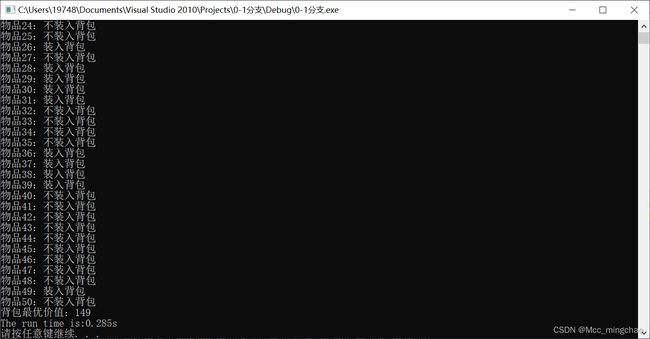
分支限界法：

1.据所学贪心算法时间复杂度只有O（n）,而考虑排序的话，就会耗费较多时间，本次实验中我采用了选择排序，时间复杂度较高，不过因为数据量不够大，且所用数据较为有序，所以贪心算法所用时间还是比较短的。2.动态规划算法的时间复杂度为O(n*c),当c较大时，其时间复杂度会比较高。3.分支限界法时间复杂度为O(2^n)，其效率不高。所以总的来看贪心算法还是比较快的，虽然其不一定能求得最优解，但其可以用较短时间来求一个近似解。

心得体会

本次实验主要是用三种方法来求解0-1背包问题，通过本次实验我对0-1背包问题有了更深刻的认识，并且对动态规划、贪心算法、分支限界三种方法也有了充分了解，对其适用的问题也较为清晰，像动态规划最重要的部分就是二维数组的构建还有要理解状态方程，贪心算法适用于最优子结构和贪心选择性质的问题，并且动态规划和贪心算法的主要区别就在于动态规划依赖于子问题的求解而贪心算法不需要，并且通过此次实验，我对于贪心算法不一定能求得最优解也有了更深刻的认识，贪心算法是求局部最优解的很好的算法，对于求最优解并不是最好的选择，同时通过本次实验我对三种方法的时间复杂度也较为熟练的掌握。

附录

动态规划

#include
#include
using namespace std;
#define max(x,y) ((x)>(y)?(x):(y))
#define MAXN 30 //最多物品数
#define MAXW 100 //最大限制重量
//问题表示
int n, W; //n个数，W容量
int w[MAXN], v[MAXN]; //物品重量和价值
//求解结果表示
int dp[MAXN][MAXW];
int x[MAXN];
int bestp; //存放最优解的总价值
//用动态规划法求0/1背包问题
void Knap()
{
int i, r;
for (i = 0; i <= n; i++) //置边界条件dp[i][0] = 0
dp[i][0] = 0;
for (r = 0; r <= W; r++) //置边界条件dp[0][r] = 0
dp[0][r] = 0;
for (i = 1; i <= n; i++) {
for (r = 1; r <= W; r++) {
if (r < w[i])
dp[i][r] = dp[i - 1][r];
else
dp[i][r] = max(dp[i - 1][r], dp[i - 1][r - w[i]] + v[i]);
}
}
}
void Buildx() //回推求最优解
{
int i = n, r = W;
bestp = 0;
while (i >= 0) {
if (dp[i][r] != dp[i - 1][r]) {
x[i] = 1;
bestp += v[i];
r = r - w[i];
}
else
x[i] = 0;
i--;
}
}
int main() {
cout << "输入物品个数n:"; cin >> n;
cout << "输入最大容量W:"; cin >> W;
cout << "依次输入每个物品的重量w和价值v，用空格分开：";
for (int i = 1; i <= n; i++) {
cin >> w[i] >> v[i];
}
Knap();
Buildx();
printf("最优方案\n");
printf("选取物品为：");
for (int i = 1; i <= n; i++)
if (x[i] == 1)
printf("%d ", i);
printf("\n");
printf("总价值=%d\n", bestp);
return 0;
}贪心：
#include
#include
#include
#include
using namespace std;
#define MAXN 51
int n;
int W;
struct NodeType
{
int w;
int v;
int p; //性价比p=v/w
bool operator<(const NodeType& s)const
{
return p > s.p;
}
};
NodeType A[MAXN];
int maxv;
int x[MAXN];
void Knap() //求解背包问题并返回总价值
{
maxv = 0; //maxv初始化为0
int weight = W; //背包中能装入的余下重量
memset(x, 0, sizeof(x)); //初始化x向量
int i = 1;
while (A[i].w <= weight) //物品i能够全部装入背包时，循环
{
x[i] = 1; //装入物品i
weight -= A[i].w; //减少背包中能装入的余下重量
maxv += A[i].v; //计算装入物品i后的总价值
i++;
}
}
void disp_bestx() {
int sumw = 0;
cout << "放入购物车的物品序号为：";
for (int j = 1; j <= n; j++) {
if (x[j] == 1) {
cout << j << " ";
sumw += A[j].w;
}
}
cout << endl;
cout << "放入购物车的物品最大价值为：" << maxv << "，总重量为：" << sumw << endl;
}
int main()
{
cout << "输入物品个数n:"; cin >> n;
cout << "输入购物车容量W:"; cin >> W;
cout << "依次输入每个物品的重量w和价值v，用空格分开：" << endl;;
for (int i = 1; i <= n; i++) {
cin >> A[i].w >> A[i].v;
}
for (int i = 1; i <= n; i++) {
A[i].p = A[i].v / A[i].w;
}
sort(A + 1, A + 1 + n);
Knap();
disp_bestx();
return 0;
}分支限界

分支限界法：
#include 
#define N 30
using namespace std;
int n;double W; //n个数，W容量
double w[N];double v[N];  //物品重量和价值
bool x[N];
bool best_x[N]; //存储最优方案
double now_v;   //当前价值
double remain_v;    //剩余价值
double now_w;   //当前容量
double best_v;  //最优价值
double Bound(int k)     //计算分枝结点k的上界
{
    remain_v = 0;
    while (k <= n) {
        remain_v += v[k];
        k++;
    }
    return remain_v + now_v;
}
void Backtrack(int t)
{
    if (t > n) {  //是否到达叶节点
        for (int i = 1; i <= n; i++) {
            best_x[i] = x[i];   //记录回溯的最优情况
        }
        best_v = now_v; //记录回溯中的最优价值
        return;
    }
    if (now_w + w[t] <= W) {  //约束条件，是否放入。放入考虑左子树，否则考虑右子树
        x[t] = 1;
        now_w += w[t];
        now_v += v[t];
        Backtrack(t + 1); //进行下一个节点的分析
        now_w -= w[t];  //在到达叶节点后进行回溯
        now_v -= v[t];
    }
    if (Bound(t + 1) > best_v) {    //限界条件，是否剪枝。若放入t后不满足约束条件则进行到此处，然后判断若当前价值加剩余价值都达不到最优，则没必要进行下去
        x[t] = 0;
        Backtrack(t + 1);
    }
}
void Knapsack(double W, int n)
{
    double sum_w = 0;
    double sum_v = 0;
    best_v = 0;
    for (int i = 0; i < n; i++) {
        sum_w += w[i];
        sum_v += v[i];
    }
    Backtrack(1);
    cout << "放入购物车的物品最大价值为：" << best_v << endl;
    cout << "放入购物车的物品序号为：" << endl;
    for (int i = 1; i <= n; i++) {
        if(x[i] == 1)
            cout << i << " ";
    }
}
int main()
{
    cout << "输入物品个数n:"; cin >> n;
    cout << "输入购物车容量W:"; cin >> W;
    cout << "依次输入每个物品的重量w和价值v，用空格分开：\n";
    for (int i = 1; i <= n; i++) {
        cin >> w[i] >> v[i];
    }
    Knapsack(W, n);
    return 0;
}