数据分析-聚类

@数据分析-聚类

目录

聚类概念

K-Means

AgglomerativeClustering

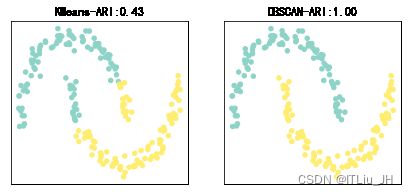
DBSCAN

MeanShift

SpectralClustering

评价

轮廓系数

兰德指数（rand index）

---

聚类概念

”物以类聚，人以群分“，聚类是典型的无监督学习方法。不同于分类，分类是有监督学习，样本都有标签，分类模型重点考查的是模型的泛化能力（predict）；而聚类是按要求给样本加标签，重点考查模型聚类的效果，通常无训练集与测试集的划分。

聚类将数据集中相似的样本分到一组，每个组称为一个簇(cluster)，相同簇的样本之间相似度较高，不同簇的样本之间相似度较低，样本之间的相似度通常是通过距离定义的，距离越远，相似度越低。

如根据学生的不同行为习惯，将学生分类，以便因才施教；根据全球各地观测到的气候特征，将全球划分为不同的气候区域 ；根据客户的消费记录将客户分成不同的消费群体。

聚类也常用于数据预处理，找出离群值。

常用的聚类方法有：K-Means，AgglomerativeClustering，DBSCAN，MeanShift，SpectralClustering等。

K-Means

K-Means聚类算法

1）从数据集中随机抽取k个样本作为初始聚类的中心，由这个中心代表各个聚类。

2）计算数据集中所有的样本到这k个中心点的距离，并将样本点归到离其最近的聚类里。

3）将聚类的中心点移动到各类的几何中心（即平均值）处。

4）重复第2步直到聚类的中心不再移动，此时算法收敛；或者迭代的次数达到上限。

kmeans算法时间、空间复杂度是：

时间复杂度：上限为O(tKmn)，下限为O（Kmn）

空间复杂度：O((m+K)n)

其中，t为迭代次数，K为簇的数目，m为样本数，n为维数

距离的度量：

欧氏距离、曼哈顿距离、闵可夫斯基距离、余弦相似度等。

如何度量样本的距离，决定了聚类的效果，需要用一个量来定量的描述，具体的距离度量方式有很多，不同的场合使用哪种需要根据不同问题具体探讨。

K值的确定：

k一般不会设置很大。可以通过枚举，令k从2到一个固定值（如8），在每个k值上重复运行数次kmeans(避免局部最优解)，并计算当前k的平均轮廓系数，最后选取轮廓系数最大的值对应的k作为最终的集群数目。

初始点的选择：

方法1：kmeans++

1、从输入的数据点集合中随机选择一个点作为第一个聚类中心
2、对于数据集中的每一个点i，计算它与最近聚类中心(指已选择的聚类中心)的距离D(i)
3、选择一个新的数据点作为新的聚类中心，选择的原则是：D(i)较大的点，被选取作为聚类中心的概率较大
4、重复2和3直到k个聚类中心被选出来
5、利用这k个初始的聚类中心来运行标准的k-means算法

方法2：选用层次聚类或Canopy算法进行初始聚类，然后从k个类别中分别随机选取k个点，来作为kmeans的初始聚类中心点

方法3：指定点​​​​​​​

用法

from sklearn.cluster import KMeans
model_km=KMeans(n_clusters=3,random_state=10).fit(data)
auto_label=model_km.labels_
auto_cluster=model_km.cluster_centers_
metrics.silhouette_score(data_auto_sc,auto_label)  #评价 

'''
KMeans(
    n_clusters=8,
    *,
    init='k-means++',
    n_init=10,
    max_iter=300,
    tol=0.0001,
    precompute_distances='deprecated',
    verbose=0,
    random_state=None,
    copy_x=True,
    n_jobs='deprecated',
    algorithm='auto',
)
'''

AgglomerativeClustering

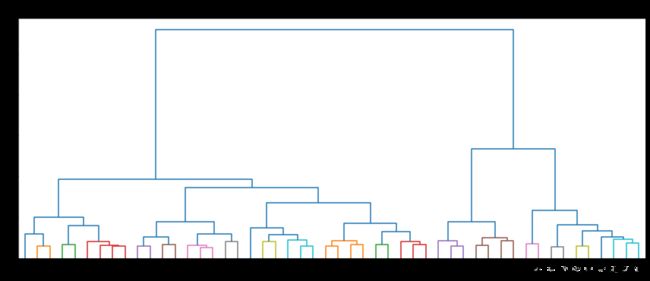
层次聚类(hierarchical clustering)有两种常用的形式，自顶向下和自底向上。
其中，自底向上的主要做法是，在开始时，将每个样本视为一个簇，重复的合并最近的两个簇，直到簇的个数达到给定值
通常用谱系图来描述簇合并的过程。

 度量簇间距离的方式有：
complete（完整连接法）：两簇之间最远的样本之间的距离
average（平均连接法）： 两簇间所有样本对的距离的平均值
single（单连接法）：两簇之间最近的样本之间的距离
ward（离差平方和法）：两簇的离差平方和之和（合并后的n*方差增量最小）

from sklearn.cluster import AgglomerativeClustering
model = AgglomerativeClustering(n_clusters=3,linkage=‘average’)
model.fit(X)  # 训练模型
auto_label = model.labels_  # 输出模型结果 

'''
AgglomerativeClustering(
    n_clusters=2,
    *,
    affinity='euclidean',
    memory=None,
    connectivity=None,
    compute_full_tree='auto',
    linkage='ward',
    distance_threshold=None,
    compute_distances=False,
)
'''

DBSCAN

DBSCAN主要思想是把样本空间中不同的高密度区域划分为不同簇。
对于一个样本点，如果在它的半径为的超球体（邻域）内的样本点个数大于，则认为这个样本点在一个高密度区域内，称这个点为核心对象。
对于两个都处在高密度区域的样本点，如果他们之间的距离足够近（即互相在对方的邻域内），则认为它们同属于一个簇。

算法：

1) 从一个点开始，对其半径为的邻域内的点赋予同一个簇标记，并寻找邻域内的其它核心对象
2) 对于找到的核心对象，重复步骤1
3) 重复上述过程直到无法找到新的高密度点为止，认为一个簇被完整找出
4) 从未被访问过的点开始，寻找下一个簇，最终没有出现在任何簇内的点被标记为孤立点。

from sklearn.cluster import DBSCAN
model = DBSCAN(eps=1.5, min_samples=4)
model.fit(X) # 训练模型
auto_label = model.labels_  # 保存模型结果
model.core_sample_indices_  # 核心对象的索引
model.components_  # 核心对象
'''
DBSCAN(
    eps=0.5,
    *,
    min_samples=5,
    metric='euclidean',
    metric_params=None,
    algorithm='auto',
    leaf_size=30,
    p=None,
    n_jobs=None,
)
'''

MeanShift

假设簇的质心在簇内点最密集的地方，寻找质心的方法是随机选择一个点(seed)，从这个点开始不断的将这个点更新为这个点邻域内点的均值点，这样，这个点就会不断的向高密度区域移动，直至到达最密集处。

1) 初始从多个起始点(seed)开始的，如果几个不同的起始点经过移动最终聚集在一起，则认为他们找了同一个簇的质心，将他们合并。

通常不使用全部样本点作为seed，而是根据窗宽bandwidth作为网格间隔，选择起始点。选好簇质心后，将样本点分到最近的簇。

2) 在更新seed点的过程中，求均值时考虑临近点与当前seed点的距离，使用高斯核函数进行加权平均，即距离越近的点权重越大。

3) 高斯核需要输入一个参数bandwidth（窗宽），用来控制seed点邻域范围的大小

Bandwidth参数可选，如果不输入，则使用estimate_bandwidth函数来计算。默认是使用样本两两之间距离的0.3分位数作为窗宽。

Seeds参数同样，若没有设置且bin_seeding=True则使用get_bin_seeds函数来计算，默认使用bandwidth作为网格大小来选择起始点。

cluster_all为True时，孤立点会被分到最近的簇内；若为False，则对孤立点标记为-1

用法：

from sklearn.cluster import MeanShift 
model = MeanShift(bandwidth=2)
model.fit(X)  
data_label = model.labels_  #样本的标签
data_cluster = model.cluster_centers_  #簇的质心
'''
MeanShift(
    *,
    bandwidth=None,
    seeds=None,
    bin_seeding=False,
    min_bin_freq=1,
    cluster_all=True,
    n_jobs=None,
    max_iter=300,
)
'''

SpectralClustering

谱聚类原理（转）

原文链接：https://blog.csdn.net/qq_24519677/article/details/82291867

谱聚类是一种基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚类，从而达到对样本数据聚类的母的。谱聚类可以理解为将高维空间的数据映射到低维，然后在低维空间用其它聚类算法（如KMeans）进行聚类。

谱聚类算法
输入：n个样本点 和聚类簇的数目k；

 输出：聚类簇

 （1）使用下面公式计算的相似度矩阵W； 

           W为组成的相似度矩阵。

 （2）使用下面公式计算度矩阵D；

          ，即相似度矩阵W的每一行元素之和

          D为组成的对角矩阵。 

（3）计算拉普拉斯矩阵； 

（4）计算L的特征值，将特征值从小到大排序，取前k个特征值，并计算前k个特征值的特征向量； 

（5）将上面的k个列向量组成矩阵，；

 （6）令是的第行的向量，其中；

（7）使用k-means算法将新样本点聚类成簇；

（8）输出簇，其中，
 

用法：

from sklearn.cluster import SpectralClustering
model= SpectralClustering(n_clusters=3)
model.fit(X)
data_label=model.labels_
'''
SpectralClustering(
    n_clusters=8,
    *,
    eigen_solver=None,
    n_components=None,
    random_state=None,
    n_init=10,
    gamma=1.0,
    affinity='rbf',
    n_neighbors=10,
    eigen_tol=0.0,
    assign_labels='kmeans',
    degree=3,
    coef0=1,
    kernel_params=None,
    n_jobs=None,
    verbose=False,
)
'''

评价

轮廓系数

评价指标-轮廓系数：

轮廓系数结合了聚类的类内凝聚度Cohesion和类间分离度Separation，用于评估聚类的效果。该值处于-1~1之间，值越大，表示聚类效果越好。

对于每个样本点i，计算点i与其同一个簇内的所有其他元素距离的平均值，记作a(i)，用于量化簇内的凝聚度。
选取i外的一个簇B，计算i与B中所有点的平均距离，遍历所有其他簇，找到最近的这个平均距离,记作B(i)，即为i的邻居类，用于量化簇之间分离度。
对于样本点i，轮廓系数
                 s(i) = (B(i) – a(i))/max{a(i),B(i)}
计算所有i的轮廓系数，求出平均值即为当前聚类的整体轮廓系数，度量数据聚类的紧密程度。

若s(i)小于0，说明i与其簇内元素的平均距离小于最近的其他簇，表示聚类效果不好。如果a(i)趋于0，或者B(i)足够大，即a(i)<

用法：

from sklearn.metrics import silhouette_score
silhouette_score(data,model.labels_)

兰德指数（rand index）

在类别信息已知的情况下可以采用兰德指数评价聚类结果

给定真实类别信息C和聚类结果K： RI=(a+b)/(a+b+c+d)

a：表示在C和K中都为同一类的样本对的数量

b：表示在C和K中都属于不同类的样本对的数量

c：表示在C中属于同一类，在K中属于不同类的样本对的数量

d：表示在C中属于不同类，在K中属于同一类的样本对的数量

取值为[0,1]，越大聚类结果与真实情况越接近

兰德指数的缺点：在聚类结果随机产生的情况下，不能保证系数接近于0

调整兰德指数（adjusted rand index）：

ARI=(RI-E(RI))/(max⁡(RI)-E(RI))

ARI取值范围为[-1,1]，负数代表结果不好，越接近于1越好

from sklearn.metrics.cluster import adjusted_rand_score
adjusted_rand_score(y,clusters)  #需要有真实的类别标签