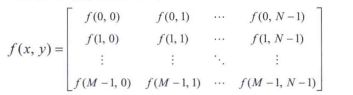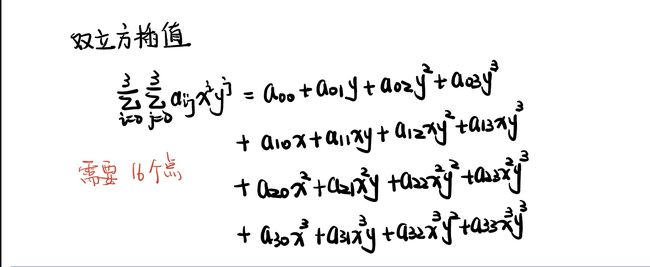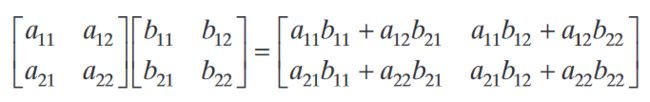2-数字图像基础
本章目标:
- 理解人类视觉的重要功能和局限
- 熟悉电磁能谱,光的性质
- 知道数字图像如何被产生和表示
- 理解图像采样和量化的基本知识
- 理解图像像素间的几何关系
- 熟悉用于数字图像处理的主要数学工具
- 能够应用多种入门的数字图像处理技术
目录
- 一、人类视觉感知
-
- 1.1 人眼构造
- 1.2 人眼成像原理
- 1.3 亮度适应与辨别
- 二、图像感知与获取
-
- 2.1 使用单个传感器获取图像
- 2.2 使用条带传感器(SENSOR STRIPS)获取图像
- 2.3 使用阵列传感器(SENSOR ARRAYS)获取图像
- 2.4 简单的成像模型
- 三、图像取样和量化
-
- 3.1 基本概念
- 3.2 数字图像表示
- 3.3 线性索引和坐标索引
- 3.4 空间分辨率和灰度分辨率
- 3.5 图像插值
-
- 3.5.1 常见的插值方法
- 四、像素间的一些基本关系
-
- 4.1 邻域(NEIGHBORS)
- 4.2 邻接(ADJACENCY)
- 4.3 连通(CONNECTIVITY)
- 4.4 区域(REGIONS)和边界(BOUNDARIES)
- 4.5 距离(DISTANCE)
- 五、图像处理的基本数学工具
-
- 5.1 利用矩阵进行ELEMENTWISE运算(ELEMENTWISE VERSUS MATRIX OPERATIONS)
- 5.2 线性运算与非线性运算(LINEAR VERSUS NONLINEAR OPERATIONS)
- 5.3 算数运算(ARITHMETIC OPERATIONS)
- 5.4 集合运算和逻辑运算(SET AND LOGICAL OPERATIONS)
- 5.5 空间运算(SPATIAL OPERATIONS)
- 5.6 向量和矩阵运算(VECTOR AND MATRIX OPERATIONS)
- 5.7 图像变换(IMAGE TRANSFORMS)
- 5.8 图像灰度和随机变量(IMAGE INTENSITIES AS RANDOM VARIABLES)
一、人类视觉感知
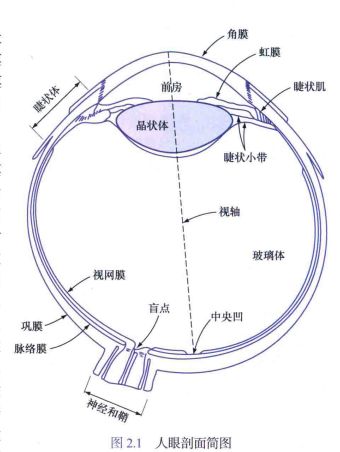
1.1 人眼构造
人眼由三层膜组成:外覆的角膜和巩膜;脉络膜;视网膜
-
角膜 (cornea): 坚硬且透明(tough, transparent),巩膜(sclera):包围眼球其余部分且不透明(opaque)
-
脉络膜(choroid):
- 位于巩膜的正下方,含有血管网——眼睛的主要营养来源;该膜只要有一点被损伤都会导致眼睛被严重伤害,因为炎症会限制血液的流动
- 颜色很深——减少进入人眼的入射光和眼球内反射光
- 最前端又分为睫状体(ciliary body)和虹膜(iris):虹膜的收缩和扩张可以控制进入人眼的光亮
-
视网膜(retina):眼睛聚焦时,来自物体的光会在视网膜上成像
- 模式视觉(pattern vision):由分布在视网膜表面上的离散的光感受器(light receptors)形成
- 光感受器有两种:锥状体(cones)和杆状体( rods)
- 视锥体:主要分布在视网膜中称为中央凹(fovea)的地方,对颜色高度敏感——视锥体视觉称为明视觉或亮视觉(photopic or bright-light vision)——肌肉控制眼球装懂,使感兴趣的图像落在中央凹上
- 视杆体:捕获视野内的整个图像;没有色觉,对低光照度敏感——暗视觉或微光视觉(scotopic or dim-light vision.)
-
晶状体(lens):
- 由同心的纤维细胞层组成,并被附在睫状体上的纤维挂起;
- 含有少量黄色色素,随着人的年龄增大而加深,极端为白内障
- 吸收约8%的可见光谱,对短波长的光有较高的吸收率;晶状体中的蛋白质吸收红外光和紫外光吸收过量会伤害眼睛
1.2 人眼成像原理
相机成像: 镜头的焦距固定,但可以调节像距(镜头与物体之间的距离是可以改变的)
人眼成像: 像距固定,但焦距可以通过改变晶状体的曲度(相当于凸透镜)来改变
1.3 亮度适应与辨别
- 人类视觉系统能够适应的光强等级范围是大的—— 从暗阈值(scotopic threshold)到眩光极限(glare limit)——约有 1 0 10 10^{10} 1010级
- 人类视觉感知的亮度即主观亮度(subjective brightness )是进入人眼的光强的对数函数(logarithmic function)
- 明视觉(Photopic Vision):人眼在明亮环境下使用的视觉分辨能力——视网膜上的视锥体;暗视觉(Scotopic Vision):人眼在暗环境下使用的视觉分辨能力——视网膜上的视杆体;中间视觉(mesopic vision):介于明视觉和暗视觉之间,此时视锥体和视杆体共同参与活动——环境亮度介于10-0.001cd/m³
- 视锥体与视杆体之间的切换是需要时间的
视错觉
- 马赫带效应(Mach bands effect):人类视觉系统有增强边缘对比度的机制,会在不同灰度区域的边界处出现“下冲”【感知“黑色”部分比“白色”部分多,亮度有一个小下降】或“上冲”现象,那么当观察两块亮度不同的区域时,边界处亮度对比加强,使轮廓表现得特别明显
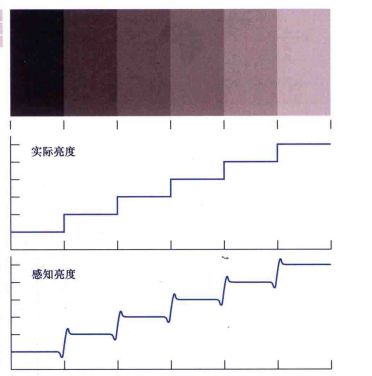
2. 同时对比(simultaneous contrast):人眼对一个区域的亮度感知不只是取决于其灰度,还会根据该区域周围的灰度

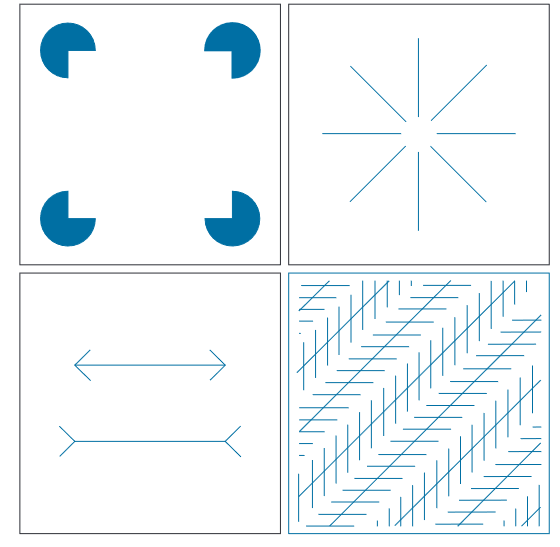
3. 光学错觉(optical illusions):
第一个:正方形的轮廓会很清晰
第二个:圆的轮廓会很清晰
第三个:线段长度虽然一样,但下面看起来很长
第四个:直线都是等距的平行线,但画上斜线会觉得不平行
二、图像感知与获取
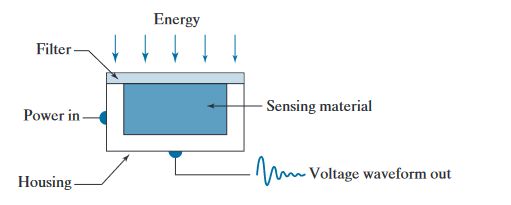
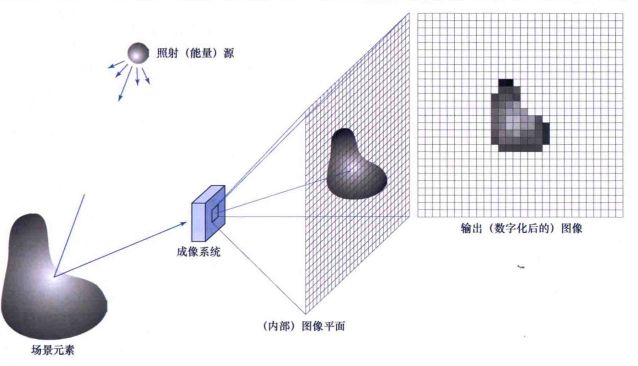
感兴趣的大多图像,是由“照明”源(illumination source)和被成像的“场景”元素(the elements of the scene)从该光源反射或吸收的能量组合产生
可以利用传感器(sensor)将照射能量转换为数字图像:将输入电能(incoming energy)同 传感器对被测能量的响应 组合在一起作为入射能量,再将入射能量转换为电压,最后输出电压波形,即对传感器响应的数字化
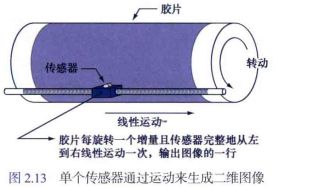
2.1 使用单个传感器获取图像
- 使用单个传感器生成二维图像时,传感器和成像区域之间必须有x方向和y方向的相对位移
- 可以用于高精度扫描 ,虽然速度慢且不便携带
具体原理:
1. 将胶片装在一个鼓(drum)上,鼓的机械运动就在一个方向上产生了位移
2. 将传感器装在产生垂直运动的引导螺杆上,传感器的线性运动会在另一个方向上产生位移
3. 鼓内含有光源,光通过胶片到达传感器前,会因胶片的密度而变化,从而导致传感器电压产生相应的变化,最后这个电压会经过数字化处理转换为灰度
2.2 使用条带传感器(SENSOR STRIPS)获取图像
具体原理:
1. 条带上布满传感器,通过其线性运动在一个方向上提供成像——一次给出二维图像的一行
2. 垂直于条带的运动在另一个方向上成像——一次给出二维图像的一列
2.3 使用阵列传感器(SENSOR ARRAYS)获取图像
具体原理:
1. 光源的能量是场景的反射,成像系统(传感器阵列)会收集这些能量并将其聚焦到一个图像平面上
2. 数字和模拟电路会将这些能量先转换成模拟信号,再进行数字化
2.4 简单的成像模型
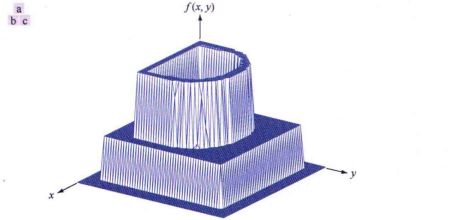
- 使用形如 f ( x , y ) f(x,y) f(x,y)的二维函数表示图像,其物理意义由图像源决定,值与物理源辐射的能量成正比——非负且有限
- f ( x , y ) f(x,y) f(x,y)由两个分量表征: f ( x , y ) = i ( x , y ) r ( x , y ) f(x,y)= i(x,y)r(x,y) f(x,y)=i(x,y)r(x,y)
- 入射到场景的光源照射量——入射分量 i ( x , y ) i(x,y) i(x,y)
- 被场景中物体反射的照射量——反射分量 r ( x , y ) r(x,y) r(x,y),被限制在0(全吸收)和1(全反射)之间
三、图像取样和量化
使用传感器获取图像最终得到的是连续的点他波形,要产生一幅数字图像,就需要把连续感测的数据转换为数字形式
3.1 基本概念
一幅图像的 x x x坐标和 y y y坐标是连续的,其幅值也是连续的,要对其函数进行数字化,就要对该函数的坐标和幅度进行取样
取样/采样 s a m p l i n g sampling sampling : 对坐标值进行数字化
量化 q u a n t i z a t i o n quantization quantization:对幅值进行数字化
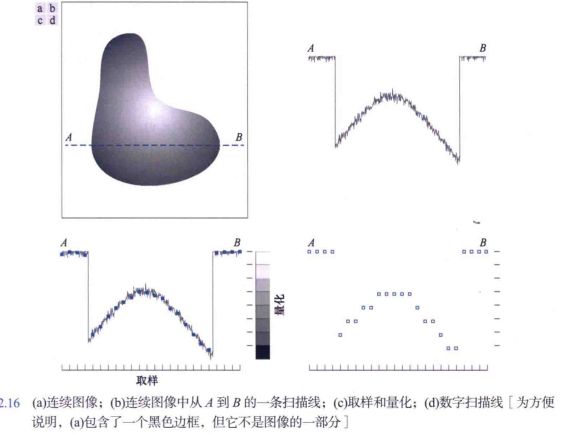
3.2 数字图像表示
- 一幅数字图像可由二维函数 f ( x , y ) f(x,y) f(x,y)表示,该图像包含 M M M行和 N N N列, ( x , y ) (x,y) (x,y)为离散坐标
- 数字图像在任何坐标 ( x , y ) (x,y) (x,y)处的值为 f ( x , y ) f(x,y) f(x,y)
- 引用特定坐标时,使用符号 ( i , j ) (i,j) (i,j)
注1: 数字图像的坐标约定:
1. 图像的左上角定义为远点
2. 大多图像显示器扫描图像时都从左上角开始向右移动,每次扫描一行
3. 正 x x x轴向下延伸,正 y y y轴向右延伸
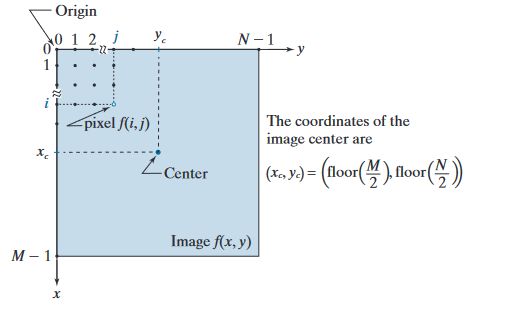
注2: 图像系统的动态范围(dynamic range):
1. 系统中最大可度量灰度与最小可检测灰度之比
2. 上限取决于饱和度(saturation),下限取决于噪声(noise)
3. 对比度(image contrast)为 一幅图像中最高和最低灰度级间的灰度差
4. 反差比(contrast ratio) 一幅图像中最高和最低灰度级间的比率
5. 一幅图像中具有高动态范围时称为高对比度,反之低对比度(灰暗)
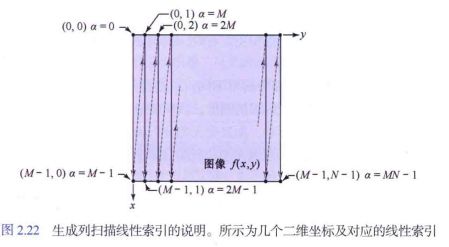
3.3 线性索引和坐标索引
- 坐标索引/下标索引(coordinate indexing,/subscript indexing): 一个像素的位置由其二维坐标给定
- 线性索引(linear indexing):
线性索引与坐标索引的转换:
图像: M × N M \times N M×N
坐标索引 -> 线性索引 : α = M y + x \alpha = My + x α=My+x
线性索引 -> 坐标索引: x = α m o d M x = \alpha \ mod \ M x=α mod M ; y = ( α − x ) / M y=(\alpha - x)/M y=(α−x)/M
3.4 空间分辨率和灰度分辨率
空间分辨率(spatial resolution):
1. 图像中最小可辨别细节的测度
2. 常用测度:单位距离的线对数(line pairs per unit distance) 和 单位距离的点数(像素数)(dots (pixels) per unit distance)
3. 空间分辨率的测度必须针对空间单位来声明才有意义【图像大小本身并不含有空间分辨率信息】
灰度分辨率(Intensity resolution):
1. 在灰度级中可分辨的最小变化
2. 灰度级通常是2的整数次幂
3. 灰度分辨率通常指量化灰度时所用的比特数,如一幅灰度被量化为256级的图像,则灰度分辨率为8比特
4. 灰度的可分辨率变化不仅受噪声和饱和度值的影响,而且受人类分析和解释整个场景内容的感知能力的影响
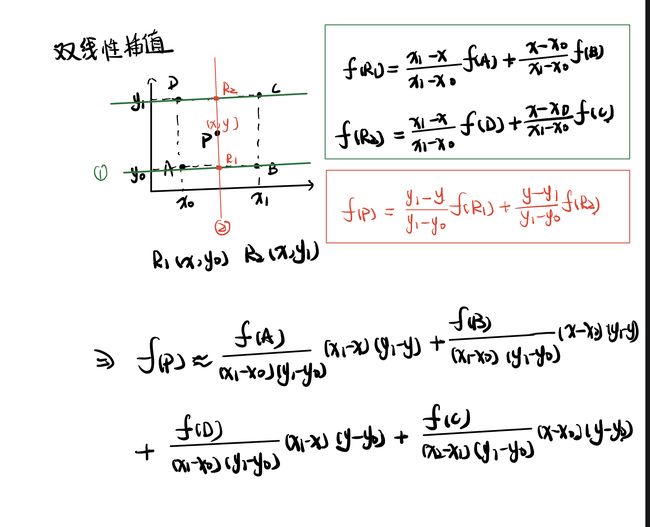
3.5 图像插值
图像插值(Image Interpolation):
1. 根据原始图像的像素值来估计周围点的像素值,达到恢复图像的完整性和原有的视觉效果
2. 通常在图像放大(zooming)、缩小(shrinking)、旋转(rotating)和几何校正(geometrically correcting)等任务中使用
3.5.1 常见的插值方法
- 最近邻插值(nearest neighbor interpolation)——零阶插值
- 原理: 原图经过几何变换得到目标图像后,目标图像上一位置(像素)上的灰度值为离其所映射到原图上的位置最近的输入像素的灰度值
- 计算公式:
x s r c = x d s t × ( W i d t h s r c / W i d t h d s t ) x_{src} = x_{dst} \times (Width_{src} / Width_{dst} ) xsrc=xdst×(Widthsrc/Widthdst)
y s r c = y d s t × ( H e i g h t s r c / H e i g h t d s t ) y_{src} = y_{dst} \times (Height_{src} / Height_{dst} ) ysrc=ydst×(Heightsrc/Heightdst)
结果不为整数,则进行四舍五入 - 优点: 算法简单, 计算量小,运算速度快
- 缺点: 没有考虑其他相邻像素点的影响,会导致重采样后亮度值有明显的不连续性,图像质量损失较大,会产生明显的马赛克和锯齿现象
def get_Nearst_Neighbor(image_path,dstHeight,dstWidth):
src_vector = plt.imread(image_path)
srcHeight = src_vector.shape[0]
srcWidth = src_vector.shape[1]
# dstHeight = ratio * srcHeight
# dstWidth = ratio * srcWidth
ratioH = dstHeight/srcHeight
ratioW = dstWidth/srcWidth
dst_vector = np.zeros(shape=(dstHeight,dstWidth,3),dtype=int)
for dst_x in range(dstHeight-1):
for dst_y in range(dstWidth-1):
src_x = round(dst_x / ratioH)
src_y = round(dst_y / ratioW)
dst_vector[dst_x][dst_y] = src_vector[src_x][src_y]
plt.show()
plt.imsave('邻近法得到的图像.jpg', dst_vector.astype(np.uint8))
实现的一种方式:
https://github.com/rootpine/Bicubic-interpolation/blob/master/bicubic.py
四、像素间的一些基本关系
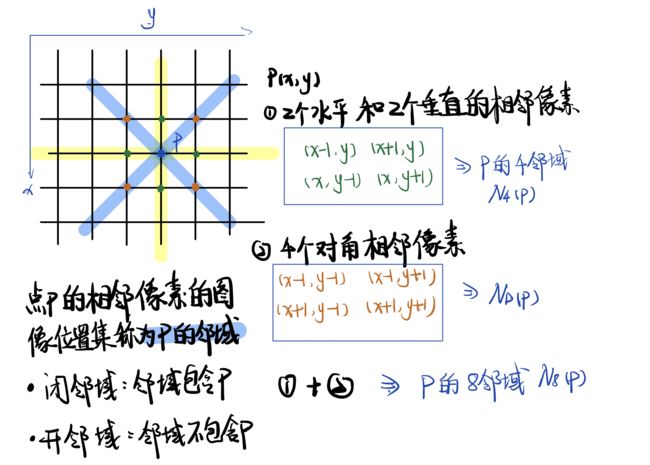
4.1 邻域(NEIGHBORS)
4.2 邻接(ADJACENCY)
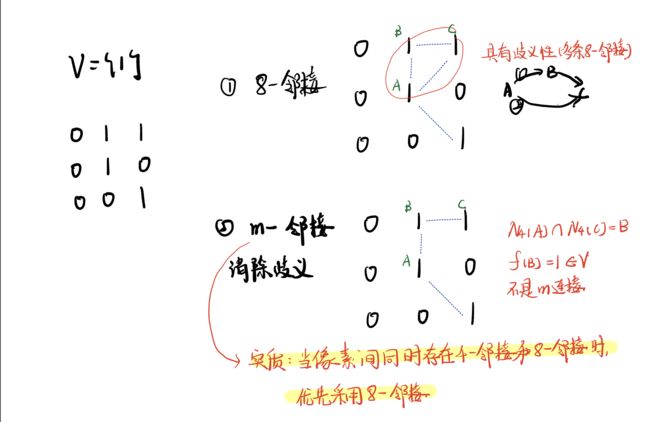
- 定义 V V V 为灰度值的集合
- p p p 和 q q q邻接:①位置关系是相邻的;②两者的灰度值都在 V V V 中
- 4邻接(4-adjacency):像素 p p p、 q q q的灰度值属于集合V, q q q在 N 4 ( p ) N_4(p) N4(p))中
- 8邻接(8-adjacency):像素 p p p、 q q q的灰度值属于集合V, q q q在 N 8 ( p ) N_8(p) N8(p))中
- m邻接(m-adjacency / mixed adjacency):像素 p p p、 q q q的灰度值属于集合V,
- 一种是: q q q在 N 4 ( p ) N_4(p) N4(p)中;
- 二种是: q q q在 N D ( p ) N_D(p) ND(p))中,且 N 4 ( p ) N_4(p) N4(p)与 N 4 ( q ) N_4(q) N4(q)的交集中没有灰度值属于 V V V
https://www.pudn.com/news/635d659f272bb74d44e3d8d9.html
4.3 连通(CONNECTIVITY)
- 若两个像素之间是邻接的,可以划一条虚线
- 若像素 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)与像素 ( x n , y n ) (x_n,y_n) (xn,yn)之间存在一个通路是指存在一个序列(digital path (or curve)) ( x 0 , y 0 ) , ( x 1 , y 1 ) , . . , ( x i , y i ) , . . , ( x n , y n ) (x_0,y_0),(x_1,y_1),..,(x_i,y_i),..,(x_n,y_n) (x0,y0),(x1,y1),..,(xi,yi),..,(xn,yn) ,其中任意相邻两点是邻接的(4邻接或8邻接或m邻接)—— 两者是连通的
- 特别地,当 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)= ( x n , y n ) (x_n,y_n) (xn,yn)时,称通路是闭合的(closed path)
通路种类:4-连通,8-连通,m-连通
使用m-邻接消除歧义性(multiple (ambiguous)):
- 令 S S S是图像中的一个像素子集
- 若 S S S中存在一个包含所有元素的通路,则意味着集合中任意两个像素是连通的
- 对 S S S中任何元素, S S S中连通到该元素的像素集合称为 S S S的一个连通分量(connected component)
- 如果 S S S仅有一个连通分量,则称 S S S为连通集(connected set)
4.4 区域(REGIONS)和边界(BOUNDARIES)
- 令 R R R是图像中的一个像素子集,若 R R R是连通集,则称 R R R为一个区域(region)
- 特别地,当谈及区域时,限制像素间的邻接类型为4邻接或8邻接
- 若两个区域 R i R_i Ri和 R j R_j Rj可以联合形成一个大区域(连通集)时,称这两个区域为邻接区域,否则为不相交区域
- 假设一幅图像含有 K K K个不相交的区域 R k R_k Rk,k = 1,2,…,并且它们都不与图像边界相接;令 R u R_u Ru表示K个区域的并集,令 ( R u ) c (R_u)^c (Ru)c表示其补集,则称 R u R_u Ru中所有点为图像前景 (foreground),而 ( R u ) c (R_u)^c (Ru)c为背景(background)
- 区域 R R R的边界(边框或轮廓)是 R R R中与 R R R的补集中的像素相邻的一组像素
- 特别地,一个区域及其背景中的点之间的邻接为8连通
补充:
- 内边界(inner border):区域内的像素
- 外边界(outer border):包围区域的像素
- 边界(boundary (or border)):整体,一个闭合通路——边框轮廓意会
- 边缘(edge):局部,导数值超过一定阈值(edges are formed from pixels with derivative values that exceed a preset threshold)——灰度值发生急剧变化(a measure of intensity-level discontinuity at a point)
4.5 距离(DISTANCE)
距离函数或指标的定义(三个条件):像素 p ( x , y ) , q ( u , v ) , s ( w , z ) p(x,y),q(u,v),s(w,z) p(x,y),q(u,v),s(w,z)
- D ( p , q ) ≥ 0 D(p,q) \geq 0 D(p,q)≥0,其中当且仅当 p = q p = q p=q时, D ( p , q ) = 0 D(p,q) = 0 D(p,q)=0
- D ( p , q ) = D ( q , s ) D(p,q) = D(q,s) D(p,q)=D(q,s)
- D ( p , s ) ≤ D ( p , q ) + D ( q , s ) D(p,s) \leq D(p,q)+D(q,s) D(p,s)≤D(p,q)+D(q,s)
-
欧式距离(圆形)
D e ( p , q ) = [ ( x − u ) 2 + ( y − v ) 2 ] 1 / 2 D_e(p,q) = [(x-u)^2 + (y-v)^2]^{1/2} De(p,q)=[(x−u)2+(y−v)2]1/2 -
城市街区距离(city-block distance)(菱形)
D 4 ( p , q ) = ∣ x − u ∣ + ∣ y − v ∣ D_4(p,q) = |x-u| + |y-v| D4(p,q)=∣x−u∣+∣y−v∣ -
棋盘距离(chessboard distance)(方形)
D 8 ( p , q ) = m a x ( ∣ x − u ∣ , ∣ y − v ∣ ) D_8(p,q) = max(|x-u|,|y-v|) D8(p,q)=max(∣x−u∣,∣y−v∣)
五、图像处理的基本数学工具
5.1 利用矩阵进行ELEMENTWISE运算(ELEMENTWISE VERSUS MATRIX OPERATIONS)
- 一幅数字图像可以视为一个矩阵
E l e m e n t w i s e Elementwise Elementwise运算:对多个图像中对应位置的像素进行逐个运算——常用符号 ⨀ \bigodot ⨀或 ⨂ \bigotimes ⨂表示
如, E l e m e n t w i s e p r o d u c t Elementwise \ product Elementwise product:对应元素的积运算——哈达玛积(Hadamard product)),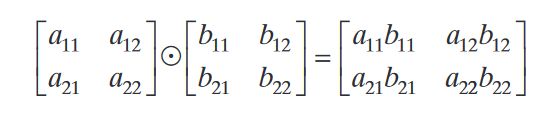
注: 矩阵乘积(matrix product)
注: 不加特殊说明,一般采用 E l e m e n t w i s e Elementwise Elementwise运算(对应元素运算)
5.2 线性运算与非线性运算(LINEAR VERSUS NONLINEAR OPERATIONS)
图片: f ( x , y ) f(x,y) f(x,y) , g ( x , y ) g(x,y) g(x,y)
算子: H H H —— 输入一幅图片输出另一幅图片
H [ f ( x , y ) ] = g ( x , y ) H[f(x,y)] = g(x,y) H[f(x,y)]=g(x,y)
线性运算:
1. 可加性(additivity)
H [ f 1 ( x , y ) + f 2 ( x , y ) ] = H [ f 1 ( x , y ) ] + H [ f 2 ( x , y ) ] H[f_1(x,y) + f_2(x,y)] = H[f_1(x,y) ] + H[f_2(x,y)] H[f1(x,y)+f2(x,y)]=H[f1(x,y)]+H[f2(x,y)]
2. 齐次性(homogeneity)
H [ a f ( x , y ) ] = a H [ f ( x , y ) ] H[af(x,y)] = aH[f(x,y)] H[af(x,y)]=aH[f(x,y)]
此时, H H H是一个线性算子,合起来看:
H [ a f 1 ( x , y ) + b f 2 ( x , y ) ] = a H [ f 1 ( x , y ) ] + b H [ f 2 ( x , y ) ] = a g 1 ( x , y ) + b g 2 ( x , y ) H[af_1(x,y)+bf_2(x,y)] = aH[f_1(x,y)]+bH[f_2(x,y)] = ag_1(x,y)+bg_2(x,y) H[af1(x,y)+bf2(x,y)]=aH[f1(x,y)]+bH[f2(x,y)]=ag1(x,y)+bg2(x,y)
如果不满足上述两个性质,就为非线性算子
5.3 算数运算(ARITHMETIC OPERATIONS)
两幅图片: f ( x , y ) f(x,y) f(x,y) , g ( x , y ) g(x,y) g(x,y)——大小相同
- 图像相加
s ( x , y ) = f ( x , y ) + g ( x , y ) s(x,y) = f(x,y) + g(x,y) s(x,y)=f(x,y)+g(x,y)
可以对同一景物重复采样多次相加取平均值来降低噪声
- 图像相减
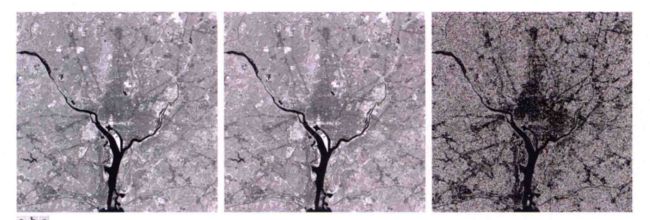
d ( x , y ) = f ( x , y ) − g ( x , y ) d(x,y) = f(x,y) - g(x,y) d(x,y)=f(x,y)−g(x,y)
- 图像相乘 or 相除
p ( x , y ) = f ( x , y ) × g ( x , y ) p(x,y) = f(x,y) \times g(x,y) p(x,y)=f(x,y)×g(x,y)
v ( x , y ) = f ( x , y ) ÷ g ( x , y ) v(x,y) = f(x,y) \div g(x,y) v(x,y)=f(x,y)÷g(x,y)
可以校正阴影,也可以得到感兴趣区域(ROI)
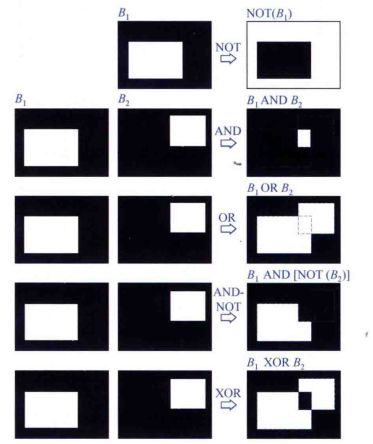
5.4 集合运算和逻辑运算(SET AND LOGICAL OPERATIONS)
5.5 空间运算(SPATIAL OPERATIONS)
-
单像素运算(Single-Pixel Operations):使用某个变换函数改变各个像素的灰度
-
邻域运算(Neighborhood Operations):以图像中任意一点为中心产生该点的邻域坐标集 S x y S_xy Sxy,使用某个变换函数作用于该坐标集中的所有点可以得到该点的输出

-
几何变换(Geometric Transformations)——橡皮模变换(rubber-sheet transformations):拉伸或收缩
两个步骤:- 坐标的空间变换 Spatial transformation of coordinates
- 灰度插值 Intensity interpolation——配给空间变换后的一些位置的像素赋予灰度值
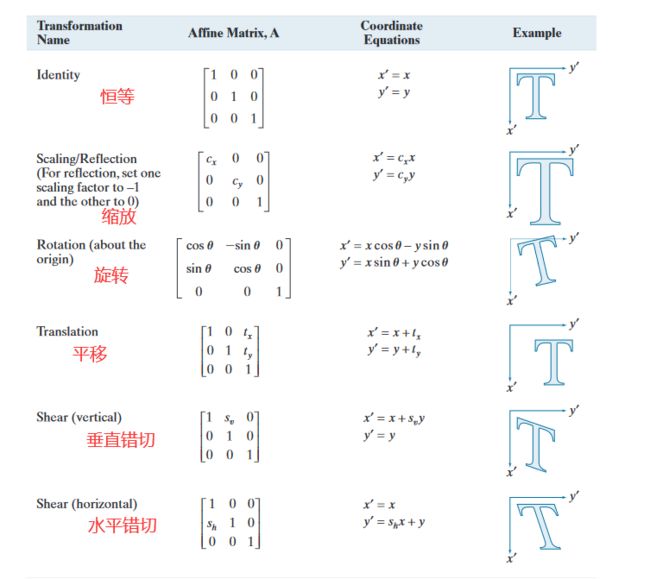
仿射变换(affine transformations)
5.6 向量和矩阵运算(VECTOR AND MATRIX OPERATIONS)
所有图像都可以当作矩阵或向量来处理
可以将一幅大小为 M × N M \times N M×N的图像表示为一个 M N × 1 MN \times 1 MN×1的列向量
5.7 图像变换(IMAGE TRANSFORMS)
上述讨论的方式都是直接在输入图像的像素上直接操作——直接在空间域上工作
图像处理的正确步骤: 变换输入图像->在变换域上执行规定的任务->执行反变换->返回空间域

理解: 这里是说将图像从空间域变换到另一种域中如时域、频域等,这个除了空间域的任何其他域都为变换域(transform domain)