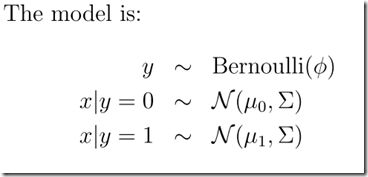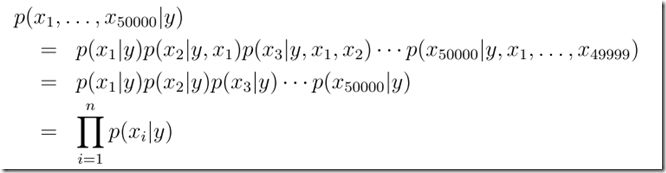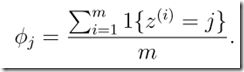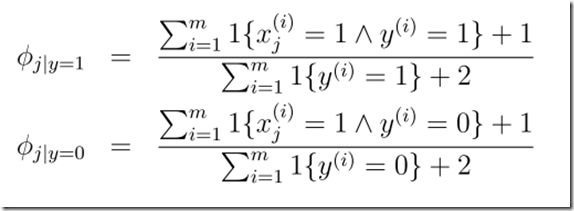【cs229-Lecture5】生成学习算法：1）高斯判别分析（GDA）;2）朴素贝叶斯（NB）

参考：

cs229讲义

机器学习（一）：生成学习算法Generative Learning algorithms：http://www.cnblogs.com/zjgtan/archive/2013/06/08/3127490.html

 

---

 

首先，简单比较一下前几节课讲的判别学习算法（Discriminative Learning Algorithm）和本节课讲的生成学习算法（Generative Learning Algorithm）的区别。

eg：问题：Consider a classification problem in which we want to learn to distinguishbetween elephants (y  =  1) and dogs (y  =  0), based on some features of
an animal.  

判别学习算法：(DLA通过建立输入空间X与输出标注{1, 0}间的映射关系学习得到p(y|x))

Given a training set,  an algorithm like logistic regression or the perceptron algorithm (basically) tries to find a straight line—that is, a decision boundary—that separates the elephants and dogs. Then, to classify a new animal as either an elephant or a dog, it checks on which side of the decision boundary it falls, and makes its prediction accordingly.

生成学习算法：(GLA首先确定p(x|y)和p(y)，由贝叶斯准则得到后验分布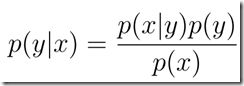,通过最大后验准则进行预测，)

First, looking at elephants, we can build a model of what elephants look like.  Then, looking at dogs, we can build a separate model of what dogs look like. Finally, to classify a new animal, we can match the new animal against the elephant model, and match it against the dog model, to see whether the new animal looks more like the elephants or more like the dogs we had seen in the training set.

 

(ps:先验概率 vs 后验概率

事情还没有发生,要求这件事情发生的可能性的大小,是

先验概率

.
事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小,是

后验概率

.

)

---

生成学习算法

首先，温习一下高斯分布的相关知识：

高斯分布      Gaussian distribution

高斯分布也就是正态分布; 数学期望为, 方差为的高斯分布通常记为.

标准正态分布      Standard normal distribution

标准正态分布是指数学期望为, 方差为的正态分布, 记为. 对于数学期望为, 方差为的正态分布随机变量, 通过下列线性变换可以得到服从标准正态分布的随机变量.

二元正态分布    Bivariate normal distribution

二元正态分布^[1]是指两个服从正态分布的随机变量具有的联合概率分布. 二元正态分布的联合概率密度函数为

其中

, , , , 为概率分布的参数. 上述二元正态分布记为.

二元正态分布的特征函数为

多元正态分布    Multivariate normal distribution

多元正态分布是指多个服从正态分布的随机变量组成的随机向量具有的联合概率分布. 数学期望为和协方差矩阵为的个随机变量的多元正态分布的联合概率密度函数为

服从多元正态分布可以记为.

如果, 并且, 那么.

 

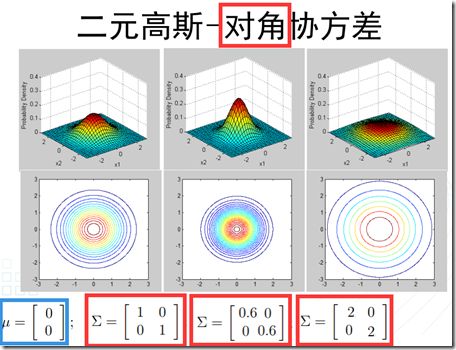
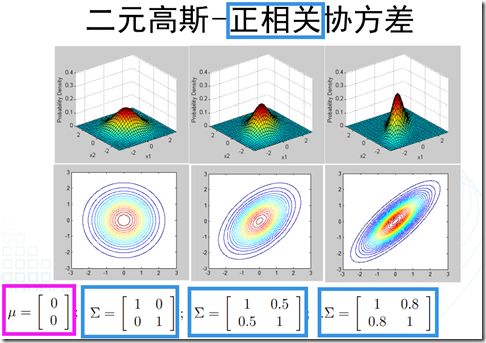
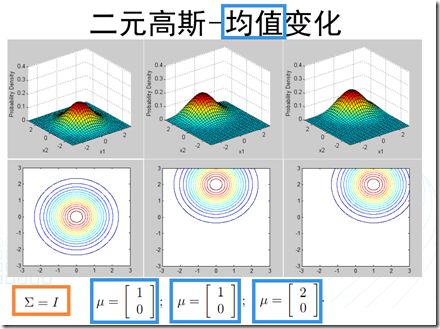
可以看到，多元正态分布与两个量相关：均值和协方差矩阵。因此，接下来，通过图像观察一下改变这两个量的值，所引起的变化。

 

 

1.   1、高斯判别分析(GDA,Gaussian Discriminant Analysis）：

       a、提出假设遵循正态分布：

                 In this model, we’ll assume that p(x|y) is distributed according to a multivariate normal distribution（多元正态分布）.

        b、分别对征服样本进行拟合，得出相应的模型

 

最后，比较一下GDA和Logistic回归

GDA——如果确实符合实际数据，则只需要少量的样本就可以得到较好的模型

Logistic Regression——Logistic回归模型有更好的鲁棒性

总结：

 GDA makes stronger modeling assumptions, and is more data efficient (i.e., requires less training data to learn “well”) when the modeling assumptions are correct or at least approximately correct.

Logistic regression makes weaker assumptions,  and is significantly more robust to deviations from modeling assumptions.

Specifically,  when the data is indeed non-Gaussian, then in the limit of large datasets, logistic regression will almost always do better than GDA. For this reason, in practice logistic regression is used more often than GDA. (Some related considerations about discriminative vs.  generative models also apply for the Naive Bayes algorithm that we discuss next, but the Naive Bayes algorithm is still considered a very good, and is certainly also a very popular, classification algorithm.)

2、朴素贝叶斯（NB,Naive Bayes）：

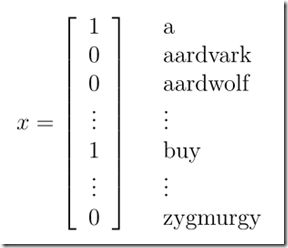
以文本分类为例，基于条件独立的假设。在实际语法上，有些单词之间是存在一定联系的，尽管如此，朴素贝叶斯还是表现出了非常好的性能。

 

因为独立，所以

 

得到联合似然函数Joint Likelihood:

得到这些参数的估计值之后，给你一封新的邮件，可以根据贝叶斯公式，计算

 

 

（可以参阅我的另一篇实战随笔：http://www.cnblogs.com/XBWer/p/3840736.html）

---

Laplace smoothing（Laplace 平滑）

当邮件中遇到新词，（0/0）本质是输入样本特征空间维数的提升，旧的模型无法提供有效分类信息。

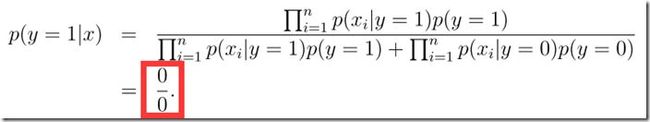
遇到这种情况时，可以进行平滑处理：（+1）

                                     ==============>