数字图像处理 实验四：图像的重建与复原

实验环境：windows11   matlab2018b

实验有借鉴成分，注意！！！

一、实验目的：

1.了解图像降质/复原处理的模型。

2.了解估计降质函数的基本原理。

3.掌握降质图像中常见噪声模型及参数估计方法、基本原理、实现步骤。

4.加深对几种常用的图像复原方法的理解。

二、实验原理：

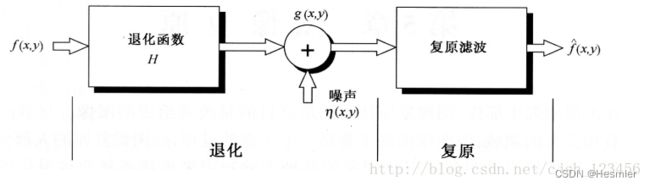
图像复原的前提是图像退化，图像退化是指图像在形成、记录、处理、传输过程中由于成像系统、记录设备、处理方法和传输介质的不完善，导致的图像质量下降。

图像复原步骤：

给出一幅退化图像，如果已知其退化的过程信息，那么对图像执行该过程的逆操作即可恢复图像。建立恰当的模型之后，使用某种概率准则对几个参数进行估计即可，此时复原变为一个检测问题。

假如退化的过程不可知或无法精确获得，则可对退化过程（模糊和噪声）建立模型，进行描述，并进而寻找一种去除或削弱其影响的过程，是一种估计方法。

在空间域中给出的退化图像一般由下式给出：

g(x,y)=h(x,y)*f(x,y)+n(x,y)

其中f(x,y)是原始图像，退化函数是h(x,y),加性噪声是n(x,y),退化图像是g(x,y).

图像复原的滤波法：

空间滤波包括：

均值滤波器，有：算术均值滤波器、几何均值滤波器、谐波均值滤波器、逆谐波均值滤波器。

统计滤波器，有：中值滤波器、最大值和最小值滤波器等。

自适应滤波器，有：自适应、局部噪声消除滤波器（需要知道或估计全部噪声的方差）、自适应中值滤波器。

  寻找滤波传递函数，通过频域图像滤波得到复原图像的傅立叶变换，再求反变换，得到复原图像。

逆滤波

在已知退化函数频谱H的情况下，由于退化过程G = F * H，那么反之，复原过程大致为F = G / H，这样虽然往往退化后的图像由于只取实部已丢失虚部信息，但还是能恢复较多的信息。

维纳滤波

维纳滤波是一种基于最小均方误差准则、对平稳过程的最优估计器。这种滤波器的输出与期望输出之间的均方误差为最小，因此，它是一个最佳滤波系统。可用于提取被平稳噪声所污染的信号。

维纳滤波的基本原理是：设观察信号y(t)含有彼此统计独立的期望信号x(t)和白噪声ω（t）可用维纳滤波从观察信号y(t)中恢复期望信号x(t)。

三、实验内容步骤：

1.使用函数进行显示模糊前后的图像：

这里使用fspecial和imfilter函数，创建滤波器进行模糊。

‘motion’：

‘dis’

效果：模糊化。

2.

这里先看一下概念：基于维纳滤波的函数deconvwnr()各个参数：

J = deconvwnr(I,psf,ncorr,icorr)

Psf是点扩散函数，ncorr是信噪比

先生成棋盘格式图像，然后创建PSF并且加入噪声。

下面计算信噪比SNR，然后进行图像的复原

图像：

3.维纳滤波和最小二乘方滤波恢复

首先退化图像

图像退化完成之后，进行图像的复原：

维纳恢复有先生成的PSF(点扩散函数)temp1,然后根据此计算图像的运动模糊。

计算完成之后，调用deconvwnr函数。

最小二乘方滤波也是先计算PSF temp2,之后退化图像计算，然后可以考虑添加高斯噪声，在计算图像对应矩阵值之后，用deconvreg函数进行图像的复原。

结果如图：

注意，这里的维纳滤波没有考虑噪声的影响，输出的图像是有噪声的。

4.

自适应中值滤波是以排序为基础的非线性技术。这种技术可以将数字图像中的一点的值用领域的各个点的中值进行替代，以此可以消除孤立的噪声点。

先编写函数：

函数的参数是原图像和需要使用的模板，这里使用11*11模板进行函数调用

先读入图像，然后进行模糊噪声处理：

然后使用主函数的调用：

先判断领域的设置，要求输入的p的值是有限制的

之后进入循环开始进行滤波：

输出之前判断输出图像的尺寸问题：

输出结果：

5.先读入图像：

输出看一下：

然后进行噪声处理：

处理结果：

然后是使用滤波处理噪声图像：

注意，在处理均值滤波的时候，需要进行归一化，否则图像无法显示。

处理结果：

从处理的结果来看，自适应中值滤波对椒盐噪声的处理是最好的，而对于高斯噪声和均匀分布噪声处理不如椒盐噪声。建议使用自适应中值滤波处理椒盐噪声效果更好。结合图像，自适应滤波可以处理更大概率的脉冲噪声，相比较与中值滤波器，自适应中值滤波处理的图像的模糊和失真相对小很多，可以更多的保护图像的细节。