Games101计算机图形学学习笔记:线性代数-向量
目录
- 一、标量与向量
-
- 1、标量
- 2、向量
-
- 1.向量的方向
- 2.向量的长度
- 3.向量的计算
-
- 1.向量加法
- 2.向量的减法
- 3.向量的乘法
-
- 1.点乘
-
- 1.在图形学中我们经常使用点乘来计算两个向量的夹角,比如制作光照模型时计算光照和法线的夹角。
- 2.另外点乘还有一个作用,就是计算一个向量在另一个向量上的投影。
- 3.通过点乘我们可以知道两个向量的是否指向同一方向
- 4.我们可以通过点乘计算两个向量有多么接近
- 2.叉乘
-
- 1.作用主要用于方便我们建立一个三维空间的直角坐标系。
- 2.第二个作用:判断一个向量在另一个向量的左还是右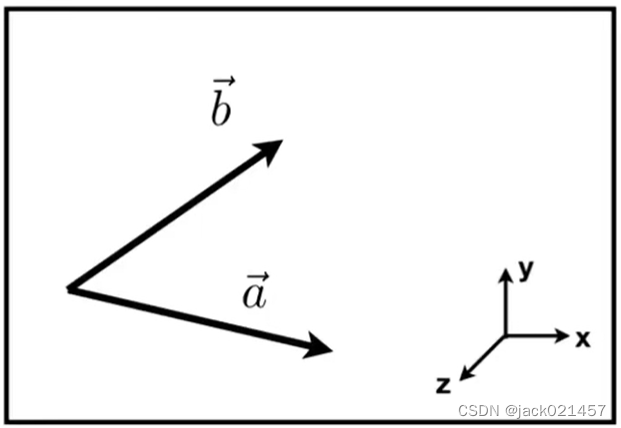
- 3.第三个作用:判断内外
- 3.点乘和叉乘的共同应用:把一个向量分解到一个三维直角坐标系上
一、标量与向量
1、标量
只有大小,没有方向的数值即称为标量。比如:长度,面积,温度等。
2、向量
又称为矢量,既有大小又有方向的量。一个向量表示一个点指向另一个点的方向和长度。向量通常可以用一个字母并在字母上加→来表示,如: a ⃗ \vec{a} a向量。

1.向量的方向
上图描述一个有 点A 指向 点B 的向量 a ⃗ \boldsymbol{\vec{a}} a 。 在同一个坐标系内,任何 a ⃗ \boldsymbol{\vec{a}} a 方向和长度相等的向量都和向量 a ⃗ \boldsymbol{\vec{a}} a 相等。比如由 点A’ 指向 点B’ 的向量 A ′ ⃗ \boldsymbol{\vec{A'}} A′ 。用向量的终点减起点即可得到这个向量的值: a ⃗ \boldsymbol{\vec{a}} a = B - A 。
2.向量的长度
向量的长度也叫向量的模,可以用两组两条|包裹的向量名来表示,如: ∣ ∣ a ⃗ ∣ ∣ \boldsymbol{||\vec{a}||} ∣∣a∣∣ 。
还有一种比较特殊的向量叫单位向量,单位向量的意思是模长为1的向量。单位向量用向量名上面加一个尖尖的角来表示,如: a ^ \boldsymbol{\hat{a}} a^。 用向量除以他自己的模长即可得到他的单位向量,也叫归一化向量: a ^ = a ⃗ / ∣ ∣ a ⃗ ∣ ∣ \boldsymbol{\hat{a} = \vec{a} / ||\vec{a}||} a^=a/∣∣a∣∣ 。
在图形学中,我们关注一个方向通常都用单位向量,并不用关心它的长度
求模公式
∣ ∣ A ⃗ ∣ ∣ = x 2 + y 2 ||\vec{A}|| = \sqrt{x^2+y^2} ∣∣A∣∣=x2+y2
这里我们还可以理解为一个向量为列矩阵乘以他的转置矩阵。
A ⃗ = ( x y ) \vec{A} = \begin{pmatrix} x \\ y \end{pmatrix} A=(xy)
A T = ( x y ) A^T = \begin{pmatrix}x&y\end{pmatrix} AT=(xy)
3.向量的计算
1.向量加法

向量加法可以用两种方式来解释,分别是平行四边形法则和三角形法则。
左边的图是平行四边形法则:
两个向量合成时,以表示这两个向量的线段为邻边作平行四边形,这个平行四边形的对角线就表示合向量的大小和方向,这就叫做平行四边形定则。
这里可以这样理解:因为向量在同一平面内可以随意移动而不会改变其值,我们可以把向量 a ⃗ \boldsymbol{\vec{a}} a和向量 b ⃗ \boldsymbol{\vec{b}} b的起点放在一起,然后再平移另一组向量 a ⃗ \boldsymbol{\vec{a}} a和向量 b ⃗ \boldsymbol{\vec{b}} b使得他们围城一个平行四边形。那么这个平行四边形的对角线就是向量 a ⃗ \boldsymbol{\vec{a}} a和向量 b ⃗ \boldsymbol{\vec{b}} b相加之和。
右边的图是三角形法则:
把向量 a ⃗ \boldsymbol{\vec{a}} a和向量 b ⃗ \boldsymbol{\vec{b}} b首尾相接,从向量 a ⃗ \boldsymbol{\vec{a}} a的起点指向向量 b ⃗ \boldsymbol{\vec{b}} b的终点的向量就是 a ⃗ \boldsymbol{\vec{a}} a+ b ⃗ \boldsymbol{\vec{b}} b的结果
这个不仅适用于两个向量,也可以用于多个向量。
2.向量的减法

将两个向量平移至公共起点,减向量的终点指向被减向量的终点的向量即为结果。
3.向量的乘法
1.点乘
1.在图形学中我们经常使用点乘来计算两个向量的夹角,比如制作光照模型时计算光照和法线的夹角。
几何解释
a ⃗ ⋅ b ⃗ = ∣ ∣ a ⃗ ∣ ∣ ∣ ∣ b ⃗ ∣ ∣ c o s θ \boldsymbol{\vec{a} \cdot \vec{b} = ||\vec{a}|| \ ||\vec{b}|| \ cosθ} a⋅b=∣∣a∣∣ ∣∣b∣∣ cosθ
两个向量点乘的结果是一个标量。
c o s θ = a ⃗ ⋅ b ⃗ ∣ ∣ a ⃗ ∣ ∣ ∣ ∣ b ⃗ ∣ ∣ \boldsymbol{cosθ = \frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| \ ||\vec{b}||}} cosθ=∣∣a∣∣ ∣∣b∣∣a⋅b
当两个向量都为单位向量时,公式可简化为
c o s θ = a ^ ⋅ b ^ \boldsymbol{cosθ = \hat{a} \cdot \hat{b}} cosθ=a^⋅b^
代数解释
a ⃗ ⋅ b ⃗ = ( x a y a ) ⋅ ( x b y b ) = x a x b + y a y b \boldsymbol{\vec{a} \cdot \vec{b} = \begin{pmatrix}x_a \\ y_a \end{pmatrix} \cdot \begin{pmatrix}x_b \\ y_b \end{pmatrix} = x_ax_b + y_ay_b} a⋅b=(xaya)⋅(xbyb)=xaxb+yayb
a ⃗ ⋅ b ⃗ = ( x a y a z a ) ⋅ ( x b y b z b ) = x a x b + y a y b + z a z b \boldsymbol{\vec{a} \cdot \vec{b} = \begin{pmatrix}x_a \\ y_a \\ z_a\end{pmatrix} \cdot \begin{pmatrix}x_b \\ y_b \\ z_b \end{pmatrix} = x_ax_b + y_ay_b + z_az_b} a⋅b=⎝ ⎛xayaza⎠ ⎞⋅⎝ ⎛xbybzb⎠ ⎞=xaxb+yayb+zazb
向量的点乘满足交换律、结合律、分配率
a ⃗ ⋅ b ⃗ = b ⃗ ⋅ a ⃗ \boldsymbol{\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}} a⋅b=b⋅a
a ⃗ ⋅ ( b ⃗ + c ⃗ ) = a ⃗ ⋅ b ⃗ + a ⃗ ⋅ c ⃗ \boldsymbol{\vec{a} \cdot (\vec{b}+\vec{c}) = \vec{a} \cdot \vec{b} + \vec{a}\cdot \vec{c}} a⋅(b+c)=a⋅b+a⋅c
( k a ⃗ ) ⋅ b ⃗ = a ⃗ ⋅ ( k b ⃗ ) = k ( a ⃗ ⋅ b ⃗ ) \boldsymbol{(k\vec{a}) \cdot \vec{b} = \vec{a} \cdot (k\vec{b}) = k(\vec{a} \cdot \vec{b})} (ka)⋅b=a⋅(kb)=k(a⋅b)
如果两个向量的点乘为0则这两个向量互相垂直 a ⃗ ⋅ b ⃗ = 0 \boldsymbol{\vec{a} \cdot \vec{b} = 0} a⋅b=0
2.另外点乘还有一个作用,就是计算一个向量在另一个向量上的投影。

投影公式的推导过程如下
b ⃗ \boldsymbol{\vec{b}} b在 a ⃗ \boldsymbol{\vec{a}} a上的投影是 b ⊥ ⃗ \boldsymbol{\vec{b_\perp}} b⊥,且两个向量的夹角是θ。因为 b ⊥ ⃗ \boldsymbol{\vec{b_\perp}} b⊥是 a ⃗ \boldsymbol{\vec{a}} a上的投影,所以 b ⊥ ⃗ \boldsymbol{\vec{b_\perp}} b⊥的方向和 a ⃗ \boldsymbol{\vec{a}} a相同。可得:
投影值为长度d乘以单位向量 a ^ \hat{a} a^ (1)
a ^ = a ⃗ ∣ ∣ a ⃗ ∣ ∣ \hat{a}=\frac{\vec{a}}{||\vec{a}||} a^=∣∣a∣∣a
b ⊥ ⃗ = d a ⃗ ∣ ∣ a ⃗ ∣ ∣ \vec{b_\perp}=d\frac{\vec{a}}{||\vec{a}||} b⊥=d∣∣a∣∣a
由三角函数可求出d的值 (2)
d = ∣ ∣ b ⃗ ∣ ∣ c o s θ d=||\vec{b}||cosθ d=∣∣b∣∣cosθ
根据点乘公式可得 (3)
c o s θ = a ⃗ ⋅ b ⃗ ∣ ∣ a ⃗ ∣ ∣ ∣ ∣ b ⃗ ∣ ∣ cosθ = \frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| \ ||\vec{b}||} cosθ=∣∣a∣∣ ∣∣b∣∣a⋅b
投影长度:把3代入2
d = ∣ ∣ b ⃗ ∣ ∣ a ⃗ ⋅ b ⃗ ∣ ∣ a ⃗ ∣ ∣ ∣ ∣ b ⃗ ∣ ∣ = a ⃗ ⋅ b ⃗ ∣ ∣ a ⃗ ∣ ∣ d=||\vec{b}||\frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| \ ||\vec{b}||}=\frac{\vec{a} \cdot \vec{b}}{||\vec{a}||} d=∣∣b∣∣∣∣a∣∣ ∣∣b∣∣a⋅b=∣∣a∣∣a⋅b
投影向量:把3代入2再,2再代入1,可得:
b ⊥ ⃗ = ∣ ∣ b ⃗ ∣ ∣ a ⃗ ⋅ b ⃗ ∣ ∣ a ⃗ ∣ ∣ ∣ ∣ b ⃗ ∣ ∣ a ⃗ ∣ ∣ a ⃗ ∣ ∣ = a ⃗ ⋅ b ⃗ ∣ ∣ a ⃗ ∣ ∣ 2 a ⃗ \vec{b_\perp}=||\vec{b}||\frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| \ ||\vec{b}||}\frac{\vec{a}}{||\vec{a}||}=\frac{\vec{a} \cdot \vec{b}}{||\vec{a}||^2}\vec{a} b⊥=∣∣b∣∣∣∣a∣∣ ∣∣b∣∣a⋅b∣∣a∣∣a=∣∣a∣∣2a⋅ba

得到向量 b ⃗ \vec{b} b在向量 a ⃗ \vec{a} a上的投影向量后,我们可根据向量减法求出另一条直角边所代表的的向量 b ⃗ − b ⃗ ⊥ \vec{b}-\vec{b}_\perp b−b⊥
3.通过点乘我们可以知道两个向量的是否指向同一方向

这里 a ⃗ \vec{a} a和 b ⃗ \vec{b} b的点乘结果大于0,我们可知他们方向基本上是一致的。 a ⃗ \vec{a} a和 c ⃗ \vec{c} c的点乘结果小于0则他们方向相反。如果点乘结果等于0则两个向量垂直。
4.我们可以通过点乘计算两个向量有多么接近
参考3。如果 a ⃗ \vec{a} a和 b ⃗ \vec{b} b的点乘结果越接近1,则两个向越接近。越接近-1则两个向量越远离
2.叉乘

几何解释
不同于点乘的结果是一个标量,叉乘的结果是一个向量。该向量同时垂直于两个相乘的向量所定义的平面。因为是一个向量所以有两个属性:一个是模长,一个是方向。模长的计算公式为:
∣ ∣ a ⃗ × b ⃗ ∣ ∣ = ∣ ∣ a ⃗ ∣ ∣ ∣ ∣ b ⃗ ∣ ∣ s i n θ ||\vec{a} \times \vec{b}|| = ||\vec{a}||||\vec{b}||sinθ ∣∣a×b∣∣=∣∣a∣∣∣∣b∣∣sinθ
方向则是由两个乘数决定的,根据右手螺旋定则,由乘数指向被乘数,拇指的方向即为叉乘结果的方向
1.作用主要用于方便我们建立一个三维空间的直角坐标系。
代数解释
a ⃗ × b ⃗ = ( y a z b − y b z a z a x b − x a z b x a y b − y a x b ) \boldsymbol{\vec{a} \times \vec{b} = \begin{pmatrix} y_az_b-y_bz_a \\ z_ax_b-x_az_b \\ x_ay_b-y_ax_b \end{pmatrix}} a×b=⎝ ⎛yazb−ybzazaxb−xazbxayb−yaxb⎠ ⎞
另一种算法是把 a ⃗ \vec{a} a写成矩阵的形式A
a ⃗ × b ⃗ = A ∗ b = ( 0 − z a y a z a 0 − x a − y a x a 0 ) ( x b y b z b ) \boldsymbol{\vec{a} \times \vec{b} = A*b= \begin{pmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0 \end{pmatrix} \begin{pmatrix} x_b\\ y_b\\ z_b \end{pmatrix}} a×b=A∗b=⎝ ⎛0za−ya−za0xaya−xa0⎠ ⎞⎝ ⎛xbybzb⎠ ⎞
向量的叉乘不满足交换律: a ⃗ × b ⃗ = − b ⃗ × a ⃗ \vec{a} \times \vec{b} = -\vec{b} \times \vec{a} a×b=−b×a
一个向量和它自己的叉乘是 0 ⃗ \vec{0} 0: a ⃗ × a ⃗ = 0 ⃗ \vec{a} \times \vec{a} = \vec{0} a×a=0。因为一个向量与它自己的夹角是0,所以sinθ=0.
a ⃗ × ( b ⃗ + c ⃗ ) = a ⃗ × b ⃗ + a ⃗ × c ⃗ \vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c} a×(b+c)=a×b+a×c
a ⃗ × ( k b ⃗ ) = k ( a ⃗ × b ⃗ ) \vec{a} \times (k \vec{b}) = k( \vec{a} \times \vec{b}) a×(kb)=k(a×b)
2.第二个作用:判断一个向量在另一个向量的左还是右
根据右手螺旋定则,如果 a ⃗ \vec{a} a和 b ⃗ \vec{b} b在xy平面内,他们两个的的叉乘结果如果是正值则证明 b ⃗ \vec{b} b在 a ⃗ \vec{a} a的左侧,反之 b ⃗ \vec{b} b在 a ⃗ \vec{a} a的右侧。
3.第三个作用:判断内外

分别用 A B ⃗ × A P ⃗ \vec{AB}\times\vec{AP} AB×AP、 B C ⃗ × B P ⃗ \vec{BC}\times\vec{BP} BC×BP、 C A ⃗ × C P ⃗ \vec{CA}\times\vec{CP} CA×CP得出每次P点都在左侧,即为在该区域内部
3.点乘和叉乘的共同应用:把一个向量分解到一个三维直角坐标系上
我们可以定义一个uvw的坐标系
∣ ∣ u ⃗ ∣ ∣ = ∣ ∣ v ⃗ ∣ ∣ = ∣ ∣ w ⃗ ∣ ∣ = 1 ||\vec{u}||=||\vec{v}||=||\vec{w}||=1 ∣∣u∣∣=∣∣v∣∣=∣∣w∣∣=1他们三个长度都为1,即为单位向量
u ⃗ ⋅ v ⃗ = v ⃗ ⋅ w ⃗ = u ⃗ ⋅ w ⃗ = 0 \vec{u}\cdot\vec{v}=\vec{v}\cdot\vec{w}=\vec{u}\cdot\vec{w} = 0 u⋅v=v⋅w=u⋅w=0三个向量互相垂直
w ⃗ = u ⃗ × v ⃗ \vec{w}=\vec{u}\times\vec{v} w=u×v叉乘结果等于第三个向量
这样我们就可以得到一个右手的三维直角坐标系。
然后我们把一个向量通过投影分解到这个直角坐标系上。
p ⃗ = ( p ⃗ ⋅ u ⃗ ) u ⃗ + ( p ⃗ ⋅ v ⃗ ) v ⃗ + ( p ⃗ ⋅ w ⃗ ) w ⃗ \vec{p}=(\vec{p}\cdot\vec{u})\vec{u}+(\vec{p}\cdot\vec{v})\vec{v}+(\vec{p}\cdot\vec{w})\vec{w} p=(p⋅u)u+(p⋅v)v+(p⋅w)w
投影公式为两个向量的点乘,因为被投的向量是单位向量所以:
在u方向上的投影向量为: ∣ ∣ p ⃗ ∣ ∣ c o s θ u ⃗ ||\vec{p}|| \ cosθ \ \vec{u} ∣∣p∣∣ cosθ u
以此类推可以得到三个方向上的投影向量。即为分解之前的向量
