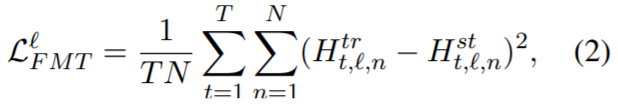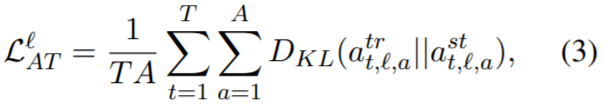模型蒸馏探索(Bert)

1. 蒸馏是什么？

​  所谓的蒸馏，指的是从大模型（通常称为teacher model）中学习小模型（通常称为student model）。何以用这个名字呢？在化学中，蒸馏是一个有效的分离沸点不同的组分的方法，大致步骤是先升温使低沸点的组分汽化，然后降温冷凝，达到分离出目标物质的目的。那么，从大模型中，通过一定的技术手段，将原模型中的知识提取出来，这个过程很类似于物质分离，所以将其称为是蒸馏。

2. 蒸馏方法

2.1 Logit Distillation

 深度学习巨头Hinton提出，是一篇开创性的工作。

 其改进是针对softmax进行的改进：

$$q_i=\frac{exp(z_i/T)}{{\sum }_{j}exp(z_j/T)}$$

 其中的T是temperature，为设定的超参数。

计算流程

 最终的loss为：

$$\begin{gathered} L=(1-\alpha )cross\_entrophy(y,p)+\alpha \ast cross\_entrophy(q,p)T^2 \\ y：真实label \\ p:studentmodel预测结果 \\ q:teachermodel预测结果 \\ \alpha :蒸馏loss权重 \\ 因为求梯度的时候会新的目标函数会导致梯度是以前的\frac{1}{T^2}，所以要再乘上T^2 \end{gathered}$$

 这个改进的motivation有一下几点：

• softmax函数自身对数据分布敏感

 对于相同的logits，当采用不同的temperature的时候，softmax之后的分布变化较大，温度越大，分布越平缓，结果的区分度越低，相当于增大了学习的难度，以后做inference的时候，temperature=1，分类结果会得到较好的提升。

• soft prediction本身带有额外的信息

 soft prediction代表teacher model对不同类别的识别概率，这个概率分布本身就带有一定的信息的，比如预测轿车的时候，识别为垃圾车和胡萝卜的概率可能都比较低，但是识别为垃圾车的概率显然要比识别为胡萝卜更高，这个信息说明垃圾车本身相比于胡萝卜与轿车的相关性更高。

 这里有人可能会好奇，为何需要先训练teacher model，然后再蒸馏到student model上面？为何不能直接训练student model？

 要注意的是，蒸馏的核心思想是好的模型不是为了拟合训练数据，而是学习如何泛化到新的数据，所以蒸馏到目的是为了让学生模型学习到教师模型的泛化能力。单纯训练学生模型的话，因为模型比较简单，所以训练难度也更大，其训练出的模型的泛化能力大概率也不如教师模型强大。

 另外注意，模型蒸馏是一种思想，理解了这篇文章的思想，可以泛化到后续的许多模型中去，因为蒸馏的使用其实本质就是各种loss function的设计。

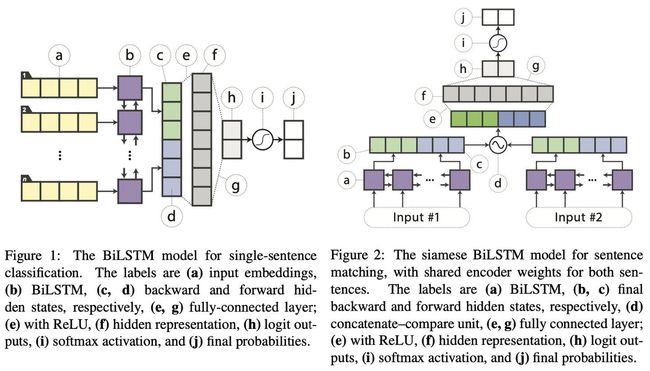
2.2 Distilled BiLSTM

 这篇文章在性能方面完全不存在竞争力，在transformer满天飞的年代，其蒸馏的结果仅仅是获得了ELMo级别的性能，不过，这篇文章最大的亮点是，在ELMo性能级别下，其使用的参数少了大约100倍，推理时间少了15倍，这对于资源敏感类任务来说可谓是一个巨大的诱惑。

Distilled BiLSTM两类任务，其teacher model使用的是BERT-large，student model为BiLSTM+Relu

 注意FIgure 2中的d操作，对于两个句子向量，其操作为：$f(h_{s1},h_{s2})=[h_{s1},h_{s2},h_{s1}\odot h_{s2},\Vert h_{s1}-h_{s2}\Vert ],\odot$代表 elementwise multiplication.

 上损失函数：

KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲\begin{aligned}…

 其中，$z^B,z^S$分别为teacher和student的logits，即预测值，$t_i$为真实one-hot类别向量$t$为第i个元素，对于无标签元素，$t_i=1ifi=argmax{y}^{B}else0$ 。

 论文中作者还提出了一些nlp领域的数据增强技术，可以看原文了解一下。

2.3 DistilBERT

这篇文章没啥难理解的地方，记录一下就行了。

 效果：模型尺寸降低40%，保留97%的泛化能力，提升了60%的速度。

 模型：teacher model为标准的Bert，student model为layers=teacher model layers/2的Bert，从teacher model的layers中每隔2层取一层初始化student model的layer。

 损失函数：公式(1)的cross entropy和masked language modeling loss，外加两模型的首层的隐状态的cos loss。

2.4 BERT-PKD

 PKD（patient knowledge distill），其teacher model为标准BERT，而student model也是BERT，不过其堆叠的层数要少于teacher。先上图为敬：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LrC5KmQ9-1632812843154)(data:image/jpeg;base64,/9j/4AAQSkZJRgABAQAAAQABAAD/2wCEAAkGBxETEhUTEhMWFRUXGBYTGBgWFxgaGhohGBkWGhoaGh0aHSoiGBolHhkYIzEhJSkrLi4xFx8zODMsNygtLisBCgoKDg0OGxAQGy0mICUvLS0vLTAtLS01LS0tKy0tLS0vLS0yLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLf/AABEIAO0A1QMBIgACEQEDEQH/xAAbAAACAwEBAQAAAAAAAAAAAAAABQMEBgIBB//EAEYQAAIBAgQDBQMICAUDBAMAAAECEQADBBIhMQUiQRMyUWFxBoGRIzNCUlOTodMUFRZicoKx0nOSsrPBNEPiJGOi8aPR4f/EABkBAAMBAQEAAAAAAAAAAAAAAAACAwEEBf/EACgRAAMAAgICAgEEAgMAAAAAAAABAgMRIUESMQRRYRMUIvBCsXGBof/aAAwDAQACEQMRAD8A+40uv8Uyi4QhItsLbGYMwp0HUcwHjPSNaY1BcwdppLW0JaM0qDMRE6a7D4CgCNcZz21yxnV366ZSg2IBk5xvHWof15hoJ7QaAHZtjkIO3g6f5h41HihGIs2xh1ZCt0l+Tk1U6AmYJiYHVfA1c/V9mI7JI2jIsem1a1oxMs0UUVhoUUUUAQYnFBCggkuSqgR0BY7kACBVX9brlutkf5IMzDknlUNAAbcg6TA0q5fsK8ZhMHMDsQYIkEagwSNOhI61VxuFVbd0pbzkq/JMBpG2pgTAFAEt7iFpIDuFJAMHfUMR7+Vv8p8KlsX1cEqZAJU+o0I9x0qlw/CI9tLj2srsilgWLEaHTNJkDMwGugY7SauYfDJbBCKFBMmPQD+gA9ABQ1oCaiiigCHF4lbdt7jmFRWdjvAUEk/AVWbiMXEttbYFwzCSp0U2gdidZuD/ACt5TeYA6HUVXGAtCCEAyggR0ByyPTlXTblHhQBwOIJ8pmlcj9n4ycivyganRvwNdYfiNpzlRwx12/dgH1AJGtUsAqXXvh7GXLciW1z8qHP5HQe4L6BhbwdsHMEAMzMdYifWNPTSta0YnsnooorDQooooArXMYoc2wCzAKzARoHLKpMkblW2+qahw/Fbb20uKCVcoq936YBBMHTcedWHwiF88c0BSQSJAJIBg6wSYnbMY3NLeK2ksWUVLT3ALllQqu8qAVUGc06AaCYJjxJrUtvSMb0MWxtoEg3FBG+o031PgJBE+R8KnVgRI2ql+qLH1OubvNvJM76GWYz4sT1NWsPZVFCIIVRAA6AbCsNJKKKKACluL4wqOUFt3KxmK5IBInLzODMEH+YUyNYD9FxBzsHAuF2aSTyt2ZVkiCCvay3hBEbCluvFbFp6NE/GJdW7C7ADDe19LL/7nlUw4+uma1dUSAWPZwJMSYuEwOpisw1vF5ozgZizToVUA2gFMpvHae8+VdpaxG9xky/SBIIy5rkjuCOQpr1ykfvVP9V/gTyZu6Sr7QpCkowzJau9MoW6LhUs2y62yJMCSNda54ZbxhCE3LYt9noGRjcmRlznMJbLvEak6HerCcLIGUCwAABAsmIAgDv7AaR4V0OfyUTLK49ZuZuUW3W3O8llQiAP41HrXOH4rYcqEcMW7sTrChvD6pB94qJ+HsSSRZJYgkm0dSIAJ59xlXXyFAwLggqLII2ItkRoRpzabn4ms1+Q2WOI40WlBjMSQqrMSTrv5AEnyU0vfjDkEdkv3n/hSridnFf+nN9kLagi1KqTqWWSZzEBW6D5JxoGqgbWLUd4EDM2kE/QyrqstHPJ3OnunkpzWkTdM0OG4rcVFXsl0UD5w9BH1KZcNxwuqTGVlOVlmY0BEHqCCD/9VjlTFHLzCOQnuhozyQeXfJA+PrTf2ZW72hLxITLcI2JzTbjwIXMSOnaDfesi3T5Nmns0tFFFUKHhMUpXjykSLV0g6g/JiR0MFwR7xNSe0mb9HfLoDAc+Ck8x9I38p61llXFAiNQRaVgxBIYH5R5J7pWAB4jYTSXfiJVND/D8XytcJs3OZww1tfURftPFTV7BcUW4+TK6NBYZsuoBAMZWO0jfxrH2ruL+qDEKZCgz2ckg5oPOQDEbGJ6WsGb4a3mjOGtZDpq0EXJA+jlzmfCdJGuLI29PQqpmqx2N7OORmkMYXL9ESe8RrVZOOWytxlDHswGI0DEEtBAJmCFkEwCDodCBHbw2IuKf0hLLEFwAC+XKdIgjWRoZ86mbBsQwNu1DaNzNrqTHd2kkx5nxqzkpssXuI2kJVnAI0jXc5dPXnTTfmFTYe+rrmQyNdfQwaoHAkzNm0cwIMu2oO8ymswJneBXOIGKRQLFqzJcE5rjRB7xPJM+evoaFOw2T8Q4mtpguVnYgtC5dAIEnMRE9PGD4UvxfFi6gCzc71ttTb+i6sfp+ApTxm3fN69BhynLB0UkDsmP1kBDyPEPoZEVb93FAzGmYqICnc2wGjN/iHcedRrI5rgm6Zpjx3/2Lnxtf30zw19XRXXusAw9/9DWIZsXryroDAGWCc5jUmQMmXXxJ0O1ab2cnI/1DcbJ+Gf3Z8/49CKIt17GmnsbUUUVQcKWYvgyu5cXLiFokLkgkCM3MhMwAN/oimdJMR7QrJFpDc/eJyofQwSfULB6GtUuuEha12VcVwy4t60iveZHz53mwMsDSAUk+dXf1Auma7dYSCVPZQYMwYtgweomlq8ee4Q6i0csiFcsNdCCQPLwq5a9oWHzlqB422zx5kFVPuEnyp3hfGpQi8R9RUdi8rqGUypEgipKmVCiiigCDGYVbi5WmJB0MEEGQQaoXuDIFJU3GIBIXPEmNBJ2mrPEeJ27MZpZjMKoljG51gAeZIFKbvtK4IAt2xOwa7DH+UIfwJpljddCU57JOEcM7Sxbe4XV2UFgHkSRuPI7++m+Cwi2lyrOpLEkyST1J69B6ACkeF41cRVTsVyqAoIumYAjY24J94ptw7ilu7IEqwElWABjxEEhh5gmJ1rbxtNvQS5L1FFFIOeOoIIIkHQg9aTrwEAAC9cgaCQh/ErJ9TTTFYlLal3MKNz6mAABqSTAAGpJpJifaWAStoBR1u3Anv0DaesGtUOuha8eyLh2Ae415Wa6gtvkUkWuYZVM93Tc6eBHnTTBcJW2+cuzkAqM2WBMSRlA10Gvr4mlNjjV0FmFpGDkP860d1V0PZmRCg++mOD46jMFdTbYkAEwVJOwDDY9BmAkmBNNWLXKQs+I2ooopCgUUUUAUsfw1bpVszIygiVy6gwYOYEHUD8fE0o4xw25bQNae67F7akE2RozAE6pvrA8yD0pnjuM27ZKwzuN1QAkddSSFUxBgmdaVYnjzPyi2uhR4N3m5WVtQEMbDr1qk422m1snXiXzwIfbXf/xfl0zw9lUVUUQqgKB4ACBSa37Q/XssPNGDAeubKfgDTfCYpLq5kaRt1BHkQdQfI60rhz0NPj0TUUUUox4RWYu8DvW9LYFxAIGuVwBsCDyt6yPStRXF68qDMzBR4sQB8TTzbn0LUp+zA4rg5JCPauBn7QqJsyZIZsvMdqaYPg2IgKEFsCdbjKSJJOi2yQY8JX1phisdg2vWrhuWSUDw2dDlkDrOk603w2Lt3Nbbq4/dYN/Q1SsjS9CKUznh+EFq2EBJiTJ3JYlmPvJJqxRRUG9lQooooAUcY4U1xu0tkB8oUhpysASRqJKkFjrB322IQY/hN4jmtOAA4LI1qOZYJ5mnQeQrbVHftKylWAZWBUg7EHQg+Iqk5WuBHCfJiOG8IufOW7dwq4LAlrIWHykbGYAGmhjMa0fCOEsj9pcIzZSgVZIAJUmSQCx5R0Eee9XOD2lWxaVQAAi6DbYGrlbeRvaQTC9hRRRUhynxTA9smXNlIIZTEwR4jqIkEeehB1rNY7hF8o1trZIZWUtaZDAYESM8Gf5T762NV8TjbVv5y4ifxMF/qapFtcIWpT5MMnCS7syJdZlcZgOzEMCbmUlo6OOuwXwp3heC3XI7QC2kgkSC5gzGnKoPjJMTsdRY4bjcHbe+Vu2lz3A051GbkSTqdeYt+NPLbhhKkEHYgyKe8jXoWZTOqKocXxVxFTswpZmKANseRyBuI1UD31VfiV0LiWPZ/IsFXlaDNu08nm11cjpt7qgUHNFK7/G0UtClgusjUaZNRGpHNAiZKMNxVzBYoXFzAEakQfIx6H1EjwJoAScQ4RdDs9sB1YlssgOCd4nRhPiRG2tI8fgHks4u282S3opOvygUShIJLXPHdRW/pLx+7hnVVuPblblpgC4BBzqCd+gJq8ZHwmTqF7QkwPC74kLbuNmYtLkKFmNOZswUR0BrScG4ebStmILOcxjYaAADx0G538tALljEo4lHVh+6Qf6VLSVkbWhlKXIUUUVMY8NYfUv8t8/9LP3h45Z2SdsulbmosRh0cZXVXHgwBHwNUx34i1OzAm5iFBhS5l4nKNm5NiN1191TkiFNwBX1Cx35k9zKc0kawpnWnuL4Jb7ezkS0tuLmdMne0EbaCN9qb4bA2rfzdtEnfKoWfgKq8qRNQ2R8JNzsU7XvwZneJOXNH0ssT5zVyiq1zH2VJDXbYK6MC6iNAdddNCD7xXOyxZoqO3iEYwrKTAeAQTBmG9DB18qkrACvDXteGgCvwz5m3/An+kVZqtwz5m3/AAJ/pFWa1+zF6CiiisNF3HmuCyezzTIzZO9l+lljWfTWJjWKyN35t2sQWhiCsHMwBiT1JO81v6qYnhti4cz2kZvrFRm+O9VjJ4rQlTsxP6ReDR2crmAnrGZgW2jYBv5vKreGLLdHYfOkqSF0BE6m4B9CJ5iNOmsU24XwZM9/tUR1FyEHMQFyIcpDGDuD6k07w+HRBlRVQeCgAfAVSsqXAqh+ylg7uLIPaWrQOYxF1ojp/wBsz+HoKn7S/wDZ2/vW/Kqe/fRBmdgo0EsQBroNTUP6xsQx7W3CAs5zrCgaktroB4moNr6KaPO0v/Z2/vW/KqDG4jFqAbdm2xzAEdqRp1MlBH4+hpkKKE19Br8mP4s7PdZL3ictsnkK6QQNrnmTMEkaUtvXLiM2RMyhVhQMon5QkSAfqoP5632Iw6OMrqrr4MAR8DSLjnBlCKbCqrdpaB57irBdQQApgTMehNWjIuJJ1HYhs82ZrlsKVYgMd4EcwJAK/wD8rUezd641s5iWUNFtm3ZYHU6sJmGO/nubNrg+HUgi0pI1BYZiPQtJFXqXJkVLQ0xphRRRURzwmszd47dua28ttDqCRmcg7HXRfSG/4rT0kxHs8uptObf7pGZB6CQR6BoHQCqY3Kf8hK30Z88ZuTmbEXFK5wMy2ehytsh0kdaYYbjN8AEOtweDrlJ8syAZfepqrjODst23ZKq/a9oc4tPlXZjm1IGY+dNcP7NkaPd03i2uTfUySzH3iD51ZuNciLy6LeH9ocOxVC2V2VmykajKcrSRpo2m+tV72Gw7G8xupnuzDGJQFbSso12PZKT6DwFOLOHRAqqoAUQPKpa5256RVbE+KNpmuMMSqdpbFowRmGXtCGUzoec7g7VAliyCD+lLo4eM6xoxbKJYwuuUDYCOoDU/orOA5EN32mtsB+jFbpIkmSAmpHMNy0g8umx1GkrMVxq+CM13LMmURAogSZz5iNPOtBjuD27gETbKiFKQIG8EEQR7tJMRNJeIcCdUZne26qrE8rrpGo0LTpV5ePr/ANJtUV8Fxa4Blt3w+UZYZUIGWBByhTpp16094Txc3G7N1AeCwK91gCAd9VOo0133OsJeE8Fa6i3kNtM4z7O55oJBkrB0E+laDhvCUtEtJdyIzNGg3hQNFEx5mBJMCsyOPXYT5f8AQwoooqBUq8SxotJmIJMhVA6k/wBBuSfAGs5jeOXwrOWVFUFiLahmAAk8z6N/lFafGYVLqlHEgx1IIjUEEagg9aRYn2bcgqLqspBBFxNSDvLKQP8A41XG41yJXl0K7PF3Vj/6k5mYSpFrvaJGib8sQD0NNcNx51I7YKVmC6yuXzIJMjxIIjwpXgOFds90L2YNq5lJOc6jnzAQJGZm67zT3B8BAIa6/aEEEADKkjUEiSSR5mNtJFUvwXDEny6PbnEcLiEhb6ZQ6mcwE9mwaBJGkiJqO/bwzW71sX7ardTs4VkGQZMnLrG1OlQDYASZMePj611UH49FeRDi7di4SWxSyQByuoGmfbmmObUEkEqp6QZrXEMLYU5sShDOTJdTBbzGw0Jk6CeggBxXF2yrRmUNBDCRMEbET1oXj2HIlx/HGzFbKqY0LtJE+CqO9GxMj30nxXGbhJW5eyZcj6Kir3iVgvPVDpP0TT3H8DzMXtvkZtWBGZSfGJBUnyMdYnWs9xvh5sjPe7GGKWpN1xM5lGmTQAO5Ou0+FXx+D0l7J15dl7Dccvbrct3QDBkayOmZDCn+U0+4XxAXlJgqynKynWDAOh6qQdD/AEIIpJhfZ26J1t25OYwXuSTvvlg/Gn3DsAllcqySTLM27GAJMQNgNAAKTJ4a49mz5b5LVFFFRKBSjE8ftgkW1a4RIJEBQR+8Tr/KDTYisrc4NetAKq9qgAVSpUNA2zKxAkDqCZ8BtVMalv8AkJTa9Hf6/uMystq2QuYaXid48LWm1XbXtCP+5aZfNDnA+EN8FNZm/wALY8pF5Se0Ii208zZjECDH/NMcHwvEEBRbIGvNcIUb+AJbToIG24qzmO/9ibo1tq4rKGUhlIBBBkEHYg9RXdVuG4TsrapMxJJ2ksSzGOgknTpVmuZlgooorACvDXteGgCvwz5m3/An+kVZqtwz5m3/AAJ/pFWa1+zF6CiiisNPGYASTAGsmldzj9j6Ja5/ApIPoxhT7jUvG8G121lWJlWg7NBmD/X1ArKcRsuUdGR7bFSAWUwCQYOZZXTfQ1XHE0uRKpod4bjihrhNq4AzBh3DpkRejzuppng+K2bpyo3NvlYFW03IDAEjzGlYZc+blvKQGHKsHTMTlgLPdKj3edN8NgLt0rlRkAYNncFcsGeVW5i3hpHiehpWOf8AgVWzQcXN7KosmGLQTEgcjwToYGbLVV3xAXEnM5KsBa5F1HZ2jKjLzc5cddvKrGCweIUEPiM5LEg9mo0Owjy2qfsbv2o/yD/91BpfZRMq3+IXQWyWWYDUSCCe5sD1MuIMdyTowNXMFeZll1ymSI9DuJ1j1APkNq57K99ov3f/AJVXxuGxTAC3fRDmBJ7KdBuILaz7vWhJPsG/wWcZj7VqO0cAnYbsY3hRqfcKVY3jltlARbjc9tpy5dFdWPfIOwPSqXEsHcS47srMGM51BbTorASVy6jwjWZJFIsTc52KXkWVUANc2I7SeUyBJNvpMKdutoxrSfsnVv0bO3x+x9Isn8aMAPVgMo95pmjggEEEHUEag+YrBYC6xzDMLpzHL2YzkDSAci6HfWtV7PYN7aNnGXM2YJIOXQTMaAkySBprO5NLkxqVwbNNsa0UUVEoFFeGsYcZcvAM7tr9BSVVfFSBBYg6HNOoOg2DxDoWq0aPGYJGxFi4QcyC5lIZgBIAOgMGfOmNfNHvWlBL2VJBfuqn0Gy/SI1O9M8JdIAa2z299A2ggkGV1Q7bxVXi32Ir10bild7jaqzr2dwlCFMBI1yRqW0767wTrAMGIOH8YvPkBwzkMjN2ilAjEMAMoZtAw5hJ22zb1ZYAhgcPch2DtzW9SMsH5z90fCouWiipMnXHrndGBUpbS6xbLADm4ANCdR2bT021NepxG0TAcE5skeepy+REGR0jWqt62rsWbDXCWUI3NbggZoBHawQMzb+NeDDpM/orzKtqbZ1U5gfnNeYlvUzvWaDY1rw1l8Txy9cCAI+HzLnIcLnOsELMwBpJInnXu9U+PuZYLA3BDE52Z25ROmc1VYX2I8i6Nxwz5m3/AAJ/pFWa+e4K+hYqivbIzDlOTu5QY7NtuYfjWj4Fj7huG0zZxkLgnvLBUAEjcGTE68p1PQvFrlBN9D+iiiolAoqhxvGNatZliSVWTsuYxJ/oPMisnxG84R3ZnuFVZoZjBgExlWFBO2gqkY3S2JV64NTwrCKlzEFc3NdzGWJ1Nu2dJ23+AA6Uyr5wMVbDZezIOYLmUKNSzJMhpiVPuinGGx920Vh2dSyrkcli2YgcrMZDeGseXUPWJvnYqtLo02Pxi2kzsCRKrpH0iFG5A3IqseMpku3ClwLaQ3GJABjLn0BMyV1ggecGo7OLa8vPhby5XkAlAZQgqe+OoB6j1ru7bVhcDYe4RdGV+ZNRlyx85ppppUnLRTaLl7GW0MOwU6aE66zA9TBgdYNSWrqtJUyASNPEb0ru4W205sPcaRBzMDPe3m54Mw9GI20ou4wWFlMNdOdxIUBjLCM3e1gAe4UKW+A2hvS3j+GNy2oDukXbJlIn5xY3B0kg+4dNKVcQ4ndd3VWNtUbJCxmMD6RPdBkEBYMQZ1gIsXjgrstwuQoV5N52OvaHZjpHZMd/CKrGNrVCVafB9EorC4HHM2Y27t1SrFDLloIidGLLGvhWn4Fj3uq2eMyNlzLoDoG26NrqPfpMBKxuVs1XvgZ0UUVMcKo4vhFm4czLDHdlJUnwkqRm981eorU2vQNbEx9n0n526PKbf/KTU1ngVgGWUuf32LD/AC92fOKs3I7ZNpyXPqzGa3P70bbabTrFWqZ3X2KkvoKKKKQYKKKKAIMXhLdwZbihhuJ6HxB3B8xS257PW/o3LqDwDK343FY/jTmo7/db0Ph4eenxplTXpmNJiq37PW+t2648CVH4oqn8aZYPB27Qi2oUHU+JPiSdWPma9wUdmkbZV2iNhtl0+GlTUVTftmJIKKKKUY8dQQQQCDoQdjSq77P2foF7f8Dae5WBVR6AUwxeKS2pdzCjyJ30AAGpJOkCkeJ9pSoLC2qqN2u3AsecKCI/mFPCr/EWnPZBwzhDO94XGvIEuZE1snMMqmTlSQdZ6aEdZp3g+E2bZzKst9ZiWYTvBYnKD4CBSXD8YvAswS2wch+8w+iq6GD9WZjrTDB8eViFuKbZJABnMhJ2GbQgnzAEkCZNUtWxZcjiiqfE8OblvKsTntnXaFdWI2PQHpVO3wbL2gWINhLKFiS0r2ksxjrmWTrOXyFQKDiilLYXE8oV0QBQsAk7K4O67ElD0I7PQ82lvh9u6obtWDEmRE6CBp8Z90bmSQDnG8LtXTmZebbMpKt5AkbjyMiknGOEtaQNba9cJe2hWbIgMwBOqDXoPMjpNNcfxpLbFFDXHESFiFkSMxJidtBJ1GmtKcRx535AloEFHjtSTysrajIImI99Wx+a19E68Rjb9nrf0rl1x4Fgv421U/jTSxYVFCooVRsAIFJLftC479nT9y5mPwdVH403wWMS6uZDImCCCCD4EHUHUH0IOxpbV/5DS56LFFFFTGCiiigCu5PaqNYyP4xunSI+JnwB1ixVV8VZzAm4gYAr3x1gnSfIVZVgdQZHlWsxHtFFIcHxPEMLBYWwLzACATp2DXCe9pzKV18j5Vho+opS3GAouZoYq7qAu8KsiZOhMZQdASVHWpsJxRXuG3lYGGMnyIHT1Hl4TBgAYVxe7p9D/Tyruq+JxdpdLlxFn6zBf6mgDvCnkX+FfHwHiAfiAalqthcXZaFt3EaBACuGOnvqzWsxBRRRWGlTieCF5Ms5SCGUjWCPLqNwR4E7b1nMbwXEFGQpnDApNplBgiCYuQFPvatdRTzkc+hXKZg/2eul8/YXQcwfvYfcMzfWndo9APCnGG4Fcc/KlVTQlVJLN1gmAFHjE+op7hrjEvm6PA5Y0hT4nNqTrp6aSZ6Z5aMUIXYPgtm0uVAwEs0do+7Ek/S8TU/6Ani/3lz+6rVFI6b9sbSKv6Anjc+9u/3VWxnA7VwKGN3lYOIvXdwCN80jfpBpnRQrpemHimZ/H8FuBma0QwYlirEggnU5TBzSdYMRJ1iAEPEuFvq1y3dQNkt96zEy6pHMdSbvXqF2g1vqX8bwyXLah1DAXLRgif8AuKP6Ej31SMj4TEqO0ZzAcFvrmC2mGZi/yj2wBMaDs5IGm0VpOEcP7FTLZmY5mIEDYAADwAHXxPoL9FJWR0tDKUgooopBjw1h2c3fnpZx3kbZD9UJssdDuRBk71uarYrAWrkdpbViNiQJHodx7qpjtSxanZgVv3FU/JZtX2UrorOF0ymZCg/zCrdkKqi5HYtoSVOQg+BOkiehEHwpzi+Ar29nJItkPnU3b0toIg5+WD8abYbhVhCGW2uYbMeZh/M0n8as8qSJqGUeH4nGtkzWreQoSWZmVycwCllyckrrEb/ViCw7S/8AZ2/vW/Kq3RXO6T6Kpfkqdpf+zt/et+VR2l/7O39635dW6Kzf4DRkuIYvElbf6SvYgrqEc5S0nRmG2kQkkHMe9GizEqbcG0gjmJVVAmFJAkDSTA99b9lBEESDpBpVjOCWcjdnbVWg5YLIsxoTkI0mrTlXrWibhmVts1xityyMvNBPMDlIA3UbyT7qeezV5+0ZVJa0FMySQrArCqTtpmlRoIG081jhHBbRs2zdtq7lFLZizgmBrDk706RAAAAABoANAKMmRa8QmOzqiiioFQooooAp8PibsR84ZjJvkTfLrO3e126RVyoMNbYF83VpHMTpCjqBl1B019danrWYgooorDQooooAKq8S7g/xLP8AupVqqvEu4P8AEs/7qVs+0Y/RaooorDQooooA8JrM3eO3bmtvLbQ6gkZnIOx10X0hv+K09JMR7PLvac2/3SuZB6CQR6ZoHQCqY3Kf8ha30Z88ZuTmbEXFK5wMy2ehytshESOtMMNxm+ACHW4PB1yk+WZAMvvU1VxnB2W7bslVfte0OcW3yrsxzakDMfOmuH9myNHu6bxbXJM6kElmPjqIPnVm41yTSrocYDFi7bDqCAZEHcEEqwMeBBGnhVio7FlUUKohQIAFSVzMsFFFFYAVxfPKfQ/0ruosWeRv4W/oaEBzgR8mn8K/0FT1FhhyL/CP6Cpa1+wQUUUVgFTiWNFpM0FiSFVRpJPn0G5J8Ad9qzmO43fCs5fIFBaLSqSABJ1uTmj0HpWoxmFS4hRxIMdSDpqCCNQQetI8R7OOQVFxXUggrcTUg7gspAj+Wq43GuRKVdCteNXJg4l5kCCtreSI0txMgjQ9D4UzwvHLikC6FZSQMyjKyzpJEkMPGIjwNLMBwo3nugLbU2rmUkhzJHPmAKiRmZuvietPcHwEKQ11+0IIIAGVJGoMSSSPMkbGJFUvwXDEny6HNFFFcxYKKKKACqvEu4P8Sz/upVqqvEu4P8Sz/upWz7Rj9FqiiisNCiiigCpxPHCymcqW1CwsTr6kClv7SD7G58bf99Te0/zS/wAaf81nLpOUxvBjr0/GuXPmrHSSOv4+CcktscXOPgurdjchQ3W31j97yqX9pB9jc+Nv++scOJXRlBtEk5VE5hJyXGP0IB5NtubcVJbx90xNlh3QRDTqELbgCAWI88pInap/ucn0i37bF+TccL4sLzOoRkKhW5suuYsBGUn6p+IplWb9l/nb38Fn/VerSV146dSmziyyptygooopyYiHtKvSzc+Nv+6o8R7QhkZRZuSQRqbfUR9aktru0qt8TvBVzWSWIUa5lluyzkRk0MgrHkfCuF/JyeTSS4PQXxsfim9myT2jAAHY3NBG9v8AvrpfaRZUdjcGZkSZTTOwUEw20kVkf0+7J+RaBmGzSYNvYxH0m9culMfpW/8AGsf7tutn5Nukmlywr42NS2t8G5ooortPPFfEeNLafJ2bscoeVyxqWA7zDXlNVv2kH2Nz42/76p+0H/UH/Ct/671JeI33QKUUtq0gAmQLdxgNAYlgonzrjy/IubcrX9R3YfjxWNU9/wBZoLHHgrXCbNzmYMNbf1EXXm8VNTftIPsbnxt/31kDxK5LAWScpIMZp7wAMZNiCW9B4aixhMS7GGtldGMwQNHIA16lYPxpH8nJ9IdfFxfk3fD8WLtsOAVnMIMSMrFTsY3FWaWezn/Tr/Fd/wBx6Z13L0ee1phUWKvhEZyCQqsxA35QTp8Klqlxr/p73+Hc/wBDUy9mMX/tIPsbnxt/31Di+PhlAFm53kbU2/ourH6XgKSY1mCMVnMBpAk/DrVC5xO6DAsEmHIEsCQvZ7Sni/8A8epMV58/KyPlJHo18XEvezYftIPsbnxt/wB9TYLjq3Lip2brmkAkpGgJ6MTsDWQsYy4Wg2yBmKgww0BIDGRsY9RI9accJ+fterf7b0+P5F1al6EyfHiYdLZrqKKK7DhKPF8CbyZVYKQwaSuYaeUj+tKf2du/bJ9035lWuLYHEu7G1cyqbYUDOy65MQCYG2r2jI15PIT0uCv9vnLnssoUr2jzM3iTvEcyCNzA1AWGSsc17RSMtwtSymfZu79tb+6b8yj9nbv2yfdN+ZV61gL3ZWlZyWXs85Fy5J27SWmXk7aCvBbxsiWtxl1gwZzDVeQwMs7zuB50v6GP6G/cZPs94NwlrLOzXFfMEWAhWMpc9WMzm/Cm1JrOHxgAXOsDIJmWjkz6ldT3oJ8BMzo5qiSS0iVU6e2FFFVuI2na1cW2YdkdVMkQSpAMjUaxqK0wSD2buja8kedo/mUH2bu/bW/um/Mqa9w/FFboFwyyXFQ9o4yljdKk+EZk1E93yFWMPgr4ZCz6hboJLuVJZ1Ns5JEgLmEEkiQJbvVN4Yb3oss+RLWyj+zt37ZPum/Mr1PZy5mQm8kK9tyBaInI6tE9ppMRPnVh8LjBmyXF1zkZmJ72TLMqdF54gDSJBMmu1sYzMTnXKXLd6SBCKAoKQBAJjx8Z0FhhPaRjz5GtNjiiqvDluhPliC+5jbYbaDSZq1VCQm4rwZ7tztFuKvIqQULd0uZkOPrfhVT9nbv2yfdN+ZU9nAYkOCXJXMTHaPtN7T0hrXpkPgJ6wnD8QI7RyflM2l1+6UylfPUA79TtU6xRT20VnNcrSZWHs3d+2t/dN+ZR+zt37ZPum/Mq/fwuIzOyOJK2wJZwoIZ85CGQOUrG8lem9RXrGNYMM6DVCpVoIh1ZgeTUQCB49Rrpn6GP6N/cZPsv8LwhtWghbMQWJIEd5mbaTG/jVuqGCTEZibrLl5oC7bjLus7T138av1UiFQ42x2lt0mMyskxMZgRMdd6mqHGIzW3VTDFWCmSIJBjUajXrQAi/Z279sn3TfmV5+zd3ftrf3TfmVK/D8VlcC4ZKXFX5RxBYcpJ6QTuJ6VYw2BvhlLOTAvAnO5BLXFa2csiQBmEEyBAlt6l+hj+i37jJ9lL9nbv2yfdN+ZVjAcDdLiu11WCyYFsrMqV3Lnx8K7OFxYLFbggliMzE7uhjVSAAucCIiQDMZiLYxsk501zTDE+S5QUgCNT5+NbOKJe0jKzXS02OaKq8OS6FPakFuXbbuIG6D6WY+/3AqhItUUUUAFQ4jEBMs7swUfAk/AAn3VNXF20GiRMEEeooAXXONJ2dy4oLBLb3RuMwQsGA00Mr+IqH9fHM6G0VZEa7DGJVTcEry6yVBjcK4JAOhYrgLQBUW1ykZSuUZSNdI2jU/Gvb2CtMZa2jHQ8yg7AqNx4Mw9GPjQBUHFxFwFflE+gGBLcqvy9Tow0iZ6GRPGG47bYE9MwUFCXDSqtpAmZYCI6r4imAwtvLlyLlmYyiJ8Y8aju8PtNui7g6ADZgwnyzAH3UATYe8rqrr3WAYaRoRI3qSvAK9oAKKKKACiiigAooooAKo43ia22ggmArNAJIDlgCAAS3cbQeFXqiuYZGMsoOkGRMwZE+MGY8JPjQAvxfGcqgpba4S7W8qnUlbb3BHQ5goiY7wkjWucPxrPOVBIudiQWIIILyYyzlgAg9Z8ACWQwyacokMXBIkgmZInYwSPQxUZ4fZ37K34dxfFj4eLMf5j40AVsPxdHFsrHP3hmEoApYlonTQDwOYHauv1xakAZiSQAMpG5QTrEgZ1nwnXXSrb4W2YlFOUQJUaDTQeA5R8B4VzbwdpYy20EbQoEemmlAE9FFFABRRRQAUUUUAf/Z)]

两种架构.（左）PKD-skip:每2层学习一下teacher的输出.（右）PKD-last:学习teacher网络的最后六层输出。两种结果都有注意一个细节，就是最后的一层输出不参与PT loss，而是参与DS loss

 从架构图可以看出，相比于直接学习最终的输出，PKD方法还教导student model学习中间层的输出，last方法的先验假设是认为teacher model的top layers包含最丰富的信息以便指导student model，而skip的先验假设则是认为teacher model的lower layers也包含了需要被蒸馏的重要信息，从作者的结果来看，PKD-Skip 效果slightly better，作者认为PKD-Skip抓住了老师网络不同层的多样性信息。而PKD-Last抓住的更多相对来说同质化信息，因为集中在了最后几层。

 对于BERT类模型来说，由于其输入序列长度比较大，如果学习所有的tokens，不仅computationally expensive, 也可能introduce noise，又考虑到BERT的预测是只针对*“[CLS]" token的最后一层输出，所以如果student model可以获得teacher model的[CLS]的表达能力，那么它就有了teacher model的泛化能力，所以直接学习[CLS]*。

 损失函数设计：

$$L_{PKD}=(1-\alpha )L_{CE}^s+\alpha L_{DS}+\beta L_{PT}上标s代表studentmodel$$

 CE loss:

$$L_{CE}^s=-\sum _{i\in |N|}\sum _{c\in C}[I(y_i=c)\cdot log{P}^s(y_i=c|x_i;{\theta }^s)]C代表labels，N代表样本数目$$

 DS loss：

$$L_{DS}=-\sum _{i\in |N|}\sum _{c\in C}[P^t(y_i=c|x_i;\widehat{{\theta }^t})\cdot log{P}^s(y_i=c|x_i;{\theta }^s)]上标t代表teachermodel$$

 PT MSE loss：

$$L_{PT}=\sum _{i=1}^N\sum _{j=1}^M||\frac{h_{i,j}^s}{||h_{i,j}^s|{|}_2}-\frac{h_{i,I_{pt(j)}}^t}{||h_{i,I_{pt(j)}}^t|{|}_2}|{|}_2^2{I}_{pt}(j)为smodel第i层相对应的tmodel层$$

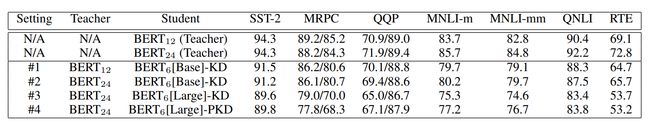
 另外，这篇paper还做了一个很有意思的实验，那就是一个更好的teacher model对于更好的蒸馏是否有效果。

 结论：

1. #1和#2对比发现，更好的teacher model并没有带来更好的效果。
2. #1和#3对比可发现，student model使用更好的model，哪怕使用更好的teacher model，效果依然变差，作者推测是压缩比（teacher model 参数量:student model参数量）更高，student model获取的信息变少了。
3. #2和#3的对比可发现，即便使用相同的teacher model，更好的student model依然表现更差，这里作者解释是初始化的缘故，因为理想的情况是对于$BER{T}_6[Base]$或者$BER{T}_6(Large)$应该是从头训练，不过由于资源受限，所以这俩模型都是使用$Ber{t}_{12}$或者$Ber{t}_{24}$的前六层参数初始化，而他们前面的六层参数可能不够捕获高层特征导致结果有差异。

 看一下这个架构，可以发现teacher model是循序渐进，一步一步教导student model去学习，而不是仅仅给出最后的答案就行了，这大概就是为何被称为patient了，这篇论文在2.3的基础上展示了中间层用于蒸馏的作用。

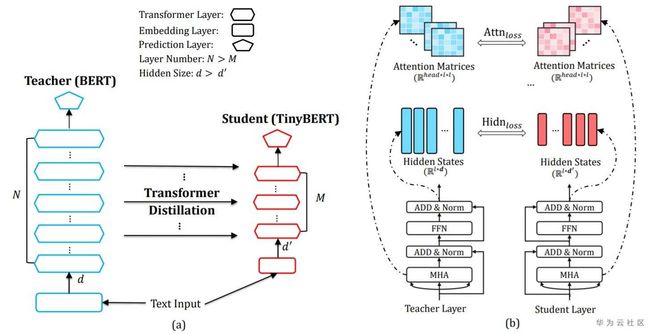
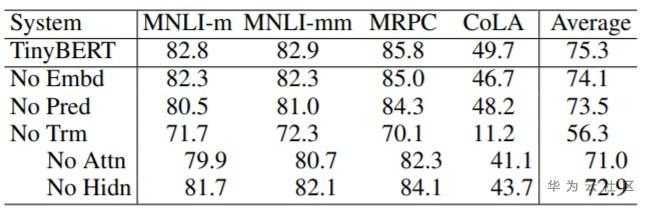
2.5 TinyBert

 上面介绍的几种蒸馏算法，实现了从embedding，中间层，到分类层的蒸馏，不过他们还只是停留在transformer block之外，没有从transformer本身出发去蒸馏，而tinybert则提出了深入到transformer内部去做蒸馏的新方法（Transformer distillation）。最终效果在 GLUE 上达到了与 BERT 相当（下降 3 个百分点）的效果，同时模型大小只有 BERT 的 13.3%（BERT 是 TinyBERT 的 7.5 倍），Inference 的速度是 BERT 的 9.4 倍。此外，TinyBERT 还显著优于当前的 SOTA 基准方法（BERT-PKD），但参数仅为为后者的 28％，推理时间仅为后者的 31％。

transformer distillation细节

 student model有N层，teacher model有M层,从M层中选择N层用于蒸馏，损失函数设计：

• embedding layer输出

$$L_{embd}=MSE(E^s{W}_e,E^t)W_e是为了保持E_s与E_t维度一致$$

• transformer层的hidden states和 attention matrices（$A=\frac{Q{K}^T}{\sqrt{d_k}}$）

 加入attention based loss的灵感来自于Clark等人的发现，即attention weights包含了substantial linguistic knowledge，这份知识很有必要transfer到student model中。

$$L_{attn}=\frac{1}{h}\sum _{i=1}^{h}MSE(A_i^s,A_i^t)h为attentionheads数目$$

$$L_{hidn}=MSE(H^s{W}_h,H^t)W_h是为了防止H^s与H^t维度不一致$$

• 预测层输出的logits

$$L_{pred}=CE(z^t/t,z^s/t)$$

 另外，这篇论文还提出了一种novel two stages 学习方式：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JWQBeemv-1632812843159)(https://i1.wp.com/syncedreview.com/wp-content/uploads/2019/10/image-23.png?w=1802&ssl=1)]

TinyBert learning

 老师网络是没有经过在具体任务进行过微调的Bert网络，然后在大规模无监督数据集上，进行Transformer distillation，当然这里的蒸馏就没有预测输出层的蒸馏。再针对具体任务进行蒸馏，老师网络是一个微调好的Bert，学生网络使用general learning之后的tinybert，对老师网络进行TD蒸馏。

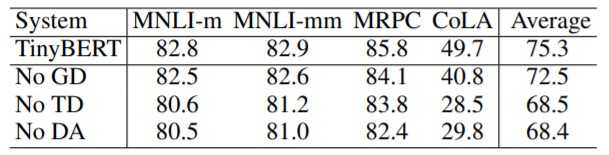
 一些结论：

 对不同蒸馏模块（GD：General Distillation、TD：Task-specific Distillation和DA：Data Augmentation）和不同类型蒸馏层（Embd: Embedding layer、Pred：Prediction layer和Trm：Transformer layer）分别进行的消融实验，结果如上表所示。实验结果表明：（1）论文提出的通用性蒸馏、任务相关性蒸馏以及数据增强对TinyBERT学习都有显著的帮助，其中任务相关蒸馏和数据增强模块在四个数据集上有持平的影响，同时两者相比通用性蒸馏模块影响更大；（2）Transformer层的蒸馏是TinyBERT学习的关键，基于注意力矩阵的蒸馏相比隐藏层的蒸馏更加重要。

2.6 MobileBert

 motivation：To the best of our knowl-edge, there is not yet any work for building a task-agnostic lightweight pre-trained model, that is, a model that can be generically fine-tuned on different downstream NLP tasks as the original BERT does. In this paper, we propose MobileBERT to fill this gap.

 想实现任务无关的蒸馏Bert看起来似乎挺容易，只要用一个大Bert去指导小的Bert直到收敛为止即可，不过，实际做的时候却会有很大的性能损失，毕竟其表达能力不够。那么，如果解决这个问题呢？mobilebert给出了自己的答案，其精妙就是上图，通过IB-BERT来蒸馏。mobilebert在保留24层的情况下，减少了4.3倍的参数，速度提升5.5倍，在GLUE上平均只比BERT-base低了0.6个点，效果好于TinyBERT和DistillBERT。

 相比于以往的蒸馏算法，MobileBert有两个方面的不同：

1. 只在pre-training阶段做蒸馏
2. 不同于以往的蒸馏算法努力从深度方面蒸馏Bert，MobileBert则是尝试在宽度方面蒸馏Bert

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5WX9Wkcx-1632812843162)(https://pbs.twimg.com/media/EVDV81yX0AE1JGB?format=jpg&name=medium)]

 模型细节如上图，MobileBert与$BER{T}_{large}$同等深度，不过每一个block更小，不同于标准的Bert，IB-BERT和MobileBert均有Linear层来做维度变换。这里引入IB-BERT的原因是直接训练MobileBert很难，所以先训练IB-BERT，再做蒸馏。

 Bottleneck的原理是在transformer的输入输出各加入一个线性层，实现维度的缩放。对于教师模型，embedding的维度是512，进入transformer后扩大为1024，而学生模型则是从512缩小至128，使得参数量骤减。采用了 bottleneck 机制的 IB-BERT 也存在问题，bottleneck 机制会打破原有的 *MHA（Multi Head Attention）*和 *FFN（Feed Forward Network）*之间的平衡，原始 bert 中的两部分的功能不同，参数比大概为 1：2。采用了 bottleneck 机制会导致 MHA 中的参数更多，所以作者在这里采用了一个堆叠 FFN 的方法，增加 FFN 的参数，Table1 中也能看出。

 为了让模型更快，作者发现最耗时间的是 Layer-Norm 和 gelu，将这两个部分进行替换。把需要均值和方差的 Layer-Norm 替换为 NoNorm （$NoNorm(h)=\gamma \odot h+\beta$）的线性操作，把 gelu 替换为 ReLU，word-embedding 降为 128，然后用一个 3 核卷积操作提高到 512。

 损失函数设计（Figure 1有标注）：

1. feature map transfer（FMT）

 由于在 BERT 中的每一层 transformer 仅获取前一层的输出作为输入，layer-wise 的知识转移中最重要的是每层都应尽可能靠近 teacher。特别是两模型每层 feature-map 之间的均方误差，T为序列长度，N为feature map size，上标为层索引：

2. attention transfer（AT）

    注意机制极大地提高了 NLP 的性能，并且成为 transformer 中至关重要的组成部分。作者使用从经过优化的 teacher 那里得到 self_attention map，帮助训练 MobileBERT。作者计算了 MobileBERT 和 IB-BERT 之间的自注意力之间的 KL 散度，A为attention heads的数目：

   

3. Pre-training Distillation (PD)

 还可以使用原始的掩码语言模型（MLM），下一句预测（NSP）和新的 MLM 知识蒸馏（KD）的线性组合作为预训练蒸馏损失。

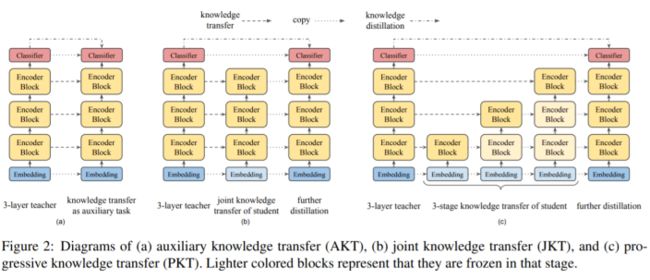
 训练策略，下面作者讨论了三种策略：

1. Auxiliary Knowledge Transfer

 这种策略下，认为中间层的knowledge transfer是用于knowledge distillation的辅助任务。使用单个loss，这个loss是所有层的knowledge transfer losses和pre-training distillation loss的线形组合。

2. Joint Knowledge Transfer

 IB-BERT 的intermediate知识（即attention map和feature map）可能不是 MobileBERT 学生的最佳解决方案。因此，作者建议将这两个 Loss 分开。首先在 MobileBERT 上训练所有 layer-wise knowledge transfer losses，然后通过pre-training distillation进一步训练它。

3. Progressive Knowledge Transfer

 作者也担心如果 MobileBERT 无法完美模仿 IB-BERT，底层可能会影响更高的层次的知识转移。因此，作者建议逐步培训知识转移的每一层。渐进式知识转移分为 L 个阶段，其中 L 是层数。

 从图可知，对于策略2和3，在layer-wise knowledge transfer阶段对于开始的embedding 层和最后的分类层没有knowledge transfer；对于3，在训练第i层的时候，会冻结它下面的所有层的可训练参数，在实践中，在训练i层的时候，并没有完全冻结下层参数，而是使用一个小的学习率去微调下层参数。

 最后的结论是逐层蒸馏效果最好，但差距最大才0.5个点，性价比有些低了。

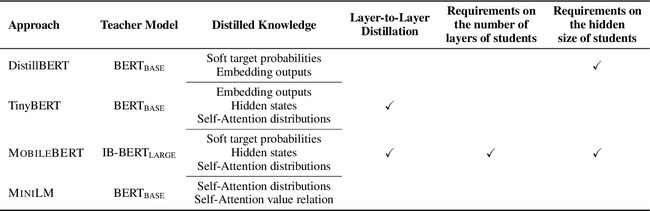
2.7 MiniLm

 来自于微软的一篇论文，论文中声称*“In particular, it retains more than 99% accuracy on SQuAD 2.0 and several GLUE benchmark tasks using 50% of the Transformer parameters and computations of the teacher model.”*

 看完上面那么多的蒸馏方法，可以发现已有的工作基本从内到外将Bert-like model和transformer蒸馏个遍，看起来似乎没啥可以蒸馏的了，不过，这篇文章确实另辟蹊跷，从最基础的self-attention modules入手作出了一些工作，具体点说，蒸馏teacher model的最后的transformer层的self-attention module，这种做法相比于以前的分层蒸馏方法而言，不再需要做teacher model和student model层之间的映射，而且student model的结构也更有弹性。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rGY5wQpf-1632812843167)(https://pbs.twimg.com/media/ERqq6X6XsAAnjU9?format=jpg&name=medium)]

 老规矩，直接看loss函数是如何设计的：

$$L=L_{AT}+L_{VR}$$

 self-attention distribution transfer(KL-divergence):

$$\begin{gathered} L_{AT}=\frac{1}{A_h|x|}\sum _{a=1}^{A_h}\sum _{t=1}^{|x|}{D}_{KL}(A_{L,a,t}^T||A_{m,a,t}^S) \\ |x|：序列长度 \\ {A}_h:attentionheads数目 \\ L:teachermodel层数 \\ M:studentmodel层数 \\ {A}_L^T:teachermodel最后一层transformer的attentiondistributions,通过queries和keys的scaleddot-product计算 \\ {A}_M^S:studentmodel最后一层transformer的attentiondistributions,通过queries和keys的scaleddot-product计算 \end{gathered}$$

 self-attention value-relation transfer:

$$\begin{gathered} V{R}_{L,a}^T=softmax(\frac{V_{L,a}^T{V}_{L,a}^{T_T}}{\sqrt{d_k}}) \\ V{R}_{M,a}^S=softmax(\frac{V_{M,a}^S{V}_{M,a}^{S_T}}{\sqrt{d_k}}) \\ {L}_{VR}=\frac{1}{A_h|x|}\sum _{a=1}^{A_h}\sum _{t=1}^{|x|}{D}_{KL}(V{R}_{L,a,t}^T||V{R}_{M,a,t}^S) \\ {V}_{L,a}^T\in R^{|x|\times d_k},V_{M,a}^S\in R^{|x|\times d_k}:teacher和studentmodel最后一个transformer层的一个attentionhead的values \\ V{R}_L^T\in R^{A_h\times |x|\times |x|},V{R}_M^S\in R^{A_h\times |x|\times |x|}:teacher和studentmodel最后一个transformer层的value-relation \end{gathered}$$

 可以发现，MiniLM的总体实现是比较简单的，它只使用了最后的transformer层，通过引入values的relation，学生网络可以更深刻的去模仿教师网络的行为，这个思路是以前别人没做过的。另外，values-relations和attention distribution都采用了scaled dot-product,还带来了另外一个好处，那就是教师网络和学生网络可以使用不同的hidden dimensions，这样的话学生网络可以更有弹性，可根据需要选择不同的hidden dimensions，从而避免了引入额外参数而改变了学生网络的表达能力。

这篇论文还使用了一个teacher assistant机制来进一步提升了效果，可以读原文了解一下。

 对比一下MiniLM和其他模型。MOBILEBERT提出使用一个特殊设计的inverted bottleneck模型，它的模型大小与$BER{T}_{LARGE}$相同，来作为教师。其他方法利用$BER{T}_{BASE}$进行实验。对于用于提炼的知识，MiniLM引入了自注意力模块中values之间的scaled dot-product作为新的知识，来深度模仿教师的自注意力行为。TinyBERT和MOBILEBERT将教师的知识层层传递给学生。MOBILEBERT假设学生的层数与教师相同。 TinyBERT采用统一的策略来确定层映射。DistillBERT用教师的参数初始化学生，因此仍然需要选择教师模型的层。MiniLM提炼出教师最后一个Transformer层的自注意力知识，使得学生的层数灵活，减轻了寻找最佳层映射的工作量.DistillBERT和MOBILEBERT的学生隐藏大小被要求与其教师相同。 TinyBERT使用参数矩阵来转换学生的隐藏状态。使用值关系允许我们的学生使用任意的隐藏大小，而不需要引入额外的参数。

 最后，好不好是看结果说话的，看一下该模型的结果：

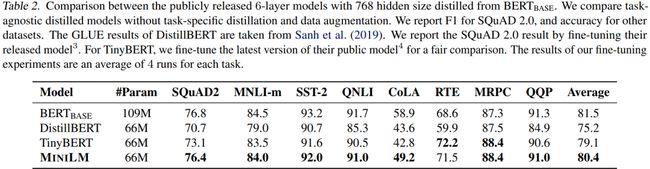
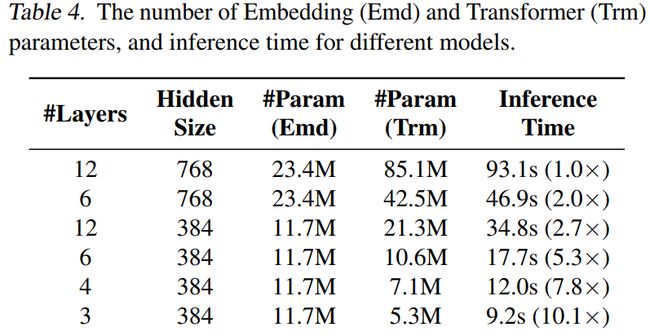
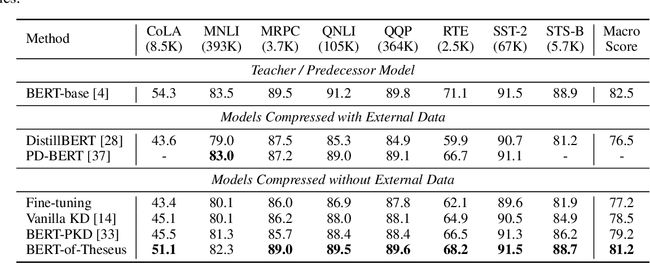
 将$BER{T}_{base}$版作为teacher，将其蒸馏为6层，768维的student模型，各个蒸馏模型在SQuAD 2.0和GLUE上的实验结果如 上Table 2所示，从实验结果可以看出，在多数任务上MiniLM都优于DistillBERT和TinyBERT。特别是在SQuAD2.0数据集和CoLA数据集上，MiniLM分别比最先进的模型高出3.0个F1值和5.0个accuracy。不同模型大小的推理时间对比可以参考下面的Table 4。

 总的来说，MiniLM是一种十分方便实现的蒸馏算法，非常推荐去尝试。

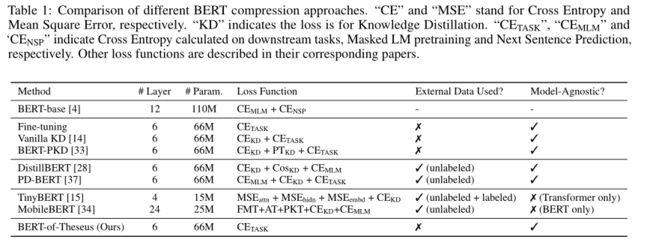
2.8 Bert-of-Theseus

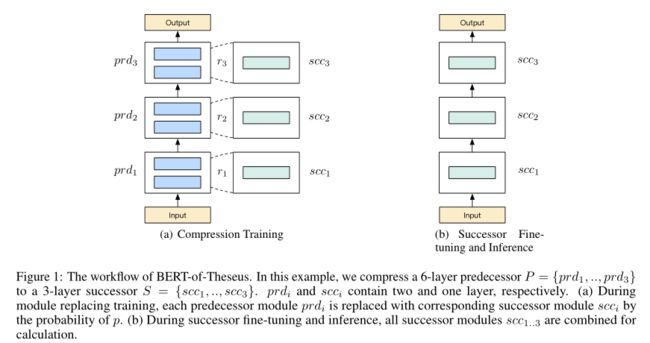
 来自于微软的文章，这篇文章思路比较清奇，因为它不像其他的蒸馏算法一样通过各种loss来实现知识迁移，而是通过渐进式模块替换来实现蒸馏效果。作者论文中声称，这个模型的灵感来自于*“ship of theseus”,即一艘船的每个部件逐渐被替换直到所有的部件都被替换一遍。Bert-of-Theseus的方法类似于ship of theseus*，他通过用更少参数的模块替换*BERT（论文中称为predecessor，对应于teacher model）*的模块从而逐步训练得到蒸馏后的模型(论文中称successor，对应于student model)。

 这篇文章的实现比较简单，从图中基本可以看懂其过程。

 假设前驱模型和后继模型都含有个模块，即$P=\{pr{d}_1,\dots ,pr{d}_n\}，S=\{sc{c}_1,\dots ,sc{c}_n\}$，其中$sc{c}_i$是用来替换$pr{d}_i$的。假设第个模块输入为$y_i$，前驱模型的前向过程可以表示为：

$$y_{i+1}=pr{d}_i(y_i)$$

 压缩时，对于第+1个模块，$r_{i+1}$是一个独立的从伯努利分布采样的变量，即以概率取值为1，以概率$1-p$取值为0:

$$r_{i+1}\sim Bernoulli(p)$$

 那么第+1个模块的输出变成

$$y_{i+1}=r_{i+1}\odot sc{c}_i(y_i)+(1-r_{i+1})\odot pr{d}_i(y_i)$$

 其中⊙表示逐元素乘操作，$r_{i+1}$∈{0,1}。通过这种方式，前驱模块和后继模块在训练时一起运作。并且由于引入了类似Dropout的随机性，也相当于为训练过程添加了正则化。

 训练的损失函数就是任务特定的损失函数，比如分类问题中的交叉熵损失函数.

 在反向传播时，所有前驱模块的权重将会被冻结，只有后继模块参数会被更新。对于前驱模型的嵌入层和输出层除了进行权重冻结外，在训练阶段还会直接当作后继模块。通过这种方式，可以在前驱模块和后继模块之间计算梯度，从而可以进行更深层次的交互。

 上面训练以后，由于每个step训练时，只会有部分不同的 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kntLh2rT-1632812843171)(https://www.zhihu.com/equation?tex=scc_i)] module参与到训练中，所有的 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jggp6Wkx-1632812843171)(https://www.zhihu.com/equation?tex=scc_i)] 并没有整合到一起参与到任务训练中。因此需要添加一个post-training过程，将所有[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-v4h2k0yB-1632812843172)(https://www.zhihu.com/equation?tex=scc_i)]重新组合成完整的transformer：

$$\begin{array}{r}S=\{sc{c}_1,\dots ,sc{c}_n\}\\ y_{i+1}=sc{c}_i(y_i)\end{array}$$

并沿用前驱模块的embedding layer和output layer（因为之前训练时这些权重参数都是freeze的，可以直接拿来用），在相同的训练数据和下游任务场景下进行finetune。

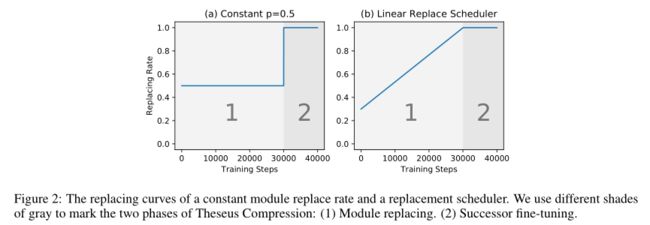
 此外，作者还提出了个渐进替换策略来提高性能，在这种策略中，替换概率随着时间增加：

$$p_d=\min (1,\theta (t))=\min (1,kt+b)$$

 其中是训练步数，>0是系数，是基本的替换概率。非渐进式替换和渐进式替换的替换概率如下图(a),(b)所示：

 通过渐进式替换策略，之前独立的训练和微调过程可以统一起来，形成一个端到端，从易到难的学习过程。在初始阶段，前驱模块作用仍然较大，使得模型损失能够平滑下降。之后，替换概率增大，逐渐过渡到了后继模块微调阶段。

 最后，看其性能：

 从其性能来看，还是非常不错的，论文声称BERT模型在保证98%性能的基础上比原模型快1.94倍，不过其训练略微繁琐，不过好处是只使用一个损失函数和一个超参数就能够进行模型压缩，省去了各种loss的组合的开销，也是一个非常不错的方法。

3.conclusion

 模型蒸馏作为模型压缩的一种手段，是一种比较有效的方法来降低模型规模。它的优点在于非常灵活，可以很方便的从一个模型迁移到另一个模型；不过，它也有自己的缺点，那就是它还需要额外的训练，这就对数据和时间提出了一定的要求，另外就是student model也需要经过精心的设计才能实现比较好的蒸馏。