点云的滤波

从零开始一起学习SLAM | 给点云加个滤网 点云下采样和去离群点

PCL—低层次视觉—点云滤波（基于点云频率） - IronStark - 博客园  基于点云频率的点云滤波

常见点云滤波算法 - 简书  常见滤波算法

点云滤波作为常见的点云处理算法，一般是点云处理的第一步，对后续处理有很重要作用。滤波有很多方面也有很多种功能，比如去除噪声点、离群点、点云平滑以及空洞、数据压缩等。

为什么要对点云滤波？

一般下面这几种情况需要进行点云滤波处理：

（1）点云数据密度不规则需要平滑

（2）因为遮挡等问题造成离群点需要去除

（3）大量数据需要下采样

（4）噪声数据需要去除

点云噪声数据来自于：

一方面来自设备。比如我们用激光扫描仪、RGB-D相机等设备获取点云数据时，由于设备精度，电磁波的衍射特性等都会引入噪声的。另一方面来自环境因素带来的影响，比如被测物体表面性质发生变化。还有一个重要的方面就是操作者经验带来的影响，比如在处理点云数据拼接配准等操作过程中引入的一些噪声等。

点云中的噪声点对后续操作的影响比较大。就像盖房子一样，地基有很多瑕疵，如果不加以处理最终可能会导致整个房子坍塌的。不过别担心，PCL中有一个专门的点云滤波模块，可以将噪声点去除，还可以进行点云压缩等操作，非常灵活实用，例如：双边滤波，统计滤波，条件滤波，随机采样一致性滤波等。这样才能够更好的进行配准，特征提取，曲面重建，可视化等后续应用处理。

一般来说，滤波对应的方案有如下几种：
（1）按照给定的规则限制过滤去除点
（2）通过常用滤波算法修改点的部分属性
（3）对数据进行下采样

一、点云数据下采样

为什么要进行下采样？

有些时候点云数据量巨大，存储、操作都很不方便，就需要进行下采样，即从大容量的点云数据样本中按一定规则选取具有代表性的样本来代替原来的大样本，可以简化操作、计算等。

PCL中的下采样类：

class  pcl::ApproximateVoxelGrid< PointT >

它比较适合对海量的点云在处理前进行数据压缩，而且可以在特征提取等处理中选择合适的体素（voxel）大小等参数，提高算法效率。该函数对输入的点云数据创建一个三维体素栅格，每个体素内用体素中所有点的重心来近似显示体素中其他点，这样该体素内所有点都用一个重心点最终表示。它的优点是可以在下采样的时候保存点云的形状特征。

二、去除点云的离群点

什么是离群点？

离群点对应的英文是outliers，也叫外点，就是明显偏离“群众”的点，比如我们用激光扫描一面平坦的墙壁，正常情况下得到的应该是差不多也位于同一个平面的点云，但是由于设备测量误差等原因，会产生少量脱离群众的空间点，离本来的墙壁过远，我们就叫这部分点为离群点。离群点会使局部点云特征(如表面法线或曲率变化)的估计复杂化，从而导致错误的值，从而可能导致点云配准失败。而且这些离群点还会随着积累进行传导，所以要在滤波环节尽可能“消灭掉”。

这里列举两个常用的去除离群点的类：

1、StatisticalOutlierRemoval

顾名思义，利用统计分析，从一个点云数据集中集中移除测量噪声点。对每个点的邻域进行统计分析，计算所有邻点的平均距离，假如得到的分布为高斯分布，我们可以计算出一个均值 μ 和一个标准差 σ，那么这个邻域点集中所有点与其邻域距离大于μ + std_mul * σ 区间之外的点都可以被视为离群点，并可从点云数据中去除。std_mul 是标准差倍数的一个阈值，可以自己指定。

示例代码：

pcl::StatisticalOutlierRemoval sor;   //创建滤波器对象
sor.setInputCloud (cloud);                           //设置待滤波的点云
sor.setMeanK (50);                               //设置在进行统计时考虑的临近点个数
sor.setStddevMulThresh (1.0);                      //设置判断是否为离群点的阀值，用来倍乘标准差，也就是上面的std_mul
sor.filter (*cloud_filtered);                    //滤波结果存储到cloud_filtered

先创建统计分析滤波器，然后设置滤波器输入是 cloud，也就是我们待处理的点云，然后设置对每个点分析的临近点的个数设置为50 ，并将标准差的倍数设置为1，  这意味着如果一个点的距离超出了平均距离加上一个标准差以上，则该点被标记为离群点，并将它移除。最后统计分析滤波后，输出的结果就是cloud_filtered

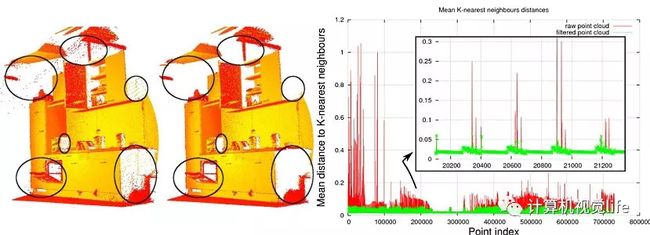
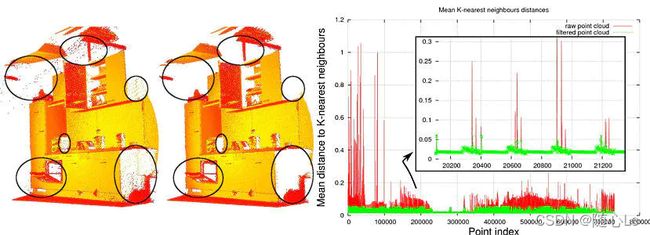
下图展示了稀疏离群值分析和移除的效果:原始数据集显示在左边，结果集显示在右边。图中红色表示滤波前的平均k近邻距离，绿色表示滤波后的平均k近邻距离，可以看到毛刺明显少了很多。

2、 RadiusOutlinerRemoval

这个类的滤波思想是根据空间点半径范围临近点数量来滤波。就是在点云数据中，设定每个点一定半径范围内周围至少有足够多的近邻，不满足就会被删除。

因为空间点的具体坐标都是知道的，所以我们可以很方便的计算某个点和它周围所有点的欧氏距离，这些都是以米为单位的，可以直接指定具体的数值，对于三维建模很实用。

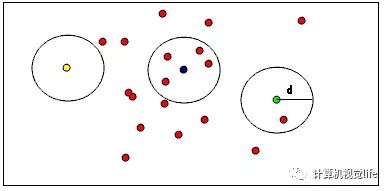
下图就是该类的筛选方法。比如你指定了一个半径d，然后指定该半径内至少有1个邻居，那么下图中只有黄色的点将从点云中删除。如果指定了半径内至少有2个邻居，那么黄色和绿色的点都将从点云中删除。

编程示例：

pcl::RadiusOutlierRemoval pcFilter;  //创建滤波器对象
pcFilter.setInputCloud(cloud);             //设置待滤波的点云
pcFilter.setRadiusSearch(0.8);               // 设置搜索半径
pcFilter.setMinNeighborsInRadius(2);      // 设置一个内点最少的邻居数目（见上面解释）
pcFilter.filter(*cloud_filtered);        //滤波结果存储到cloud_filtered

三、常见点云滤波器介绍（滤波算法）

1）直通滤波器：直通滤波器就是根据点云的属性（属性比如x，y，z，颜色值等），在点的属性上设置范围，对点进行滤波，保留范围内的或保留范围外的。可较快剪除离群点，达到第一步粗处理的目的。

举例：在一个rgbd数据中，只想保留深度值小于5米的数据，就可以通过直通滤波器来保留z属性小于5米的点云。

2）体素滤波器：体素的概念类似于像素，使用AABB包围盒将点云数据体素化，根据体素中的点，计算出代表这个体素的点，达到下采样的目的。一般体素越密集的地方信息越多，噪音点及离群点可通过体素网格去除。另一方面如果使用高分辨率相机等设备对点云进行采集，往往点云会较为密集。过多的点云数量会对后续分割工作带来困难。体素滤波器可以达到向下采样同时不破坏点云本身几何结构的功能，但会移动点的位置。

特点：可以将点云降采样至同一间距，初始密度影响不大，主要根据设置体素的大小。

3）统计滤波器：统计滤波器用于去除明显离群点。离群点特征是在空间中分布稀疏。考虑到离群点的特征，则可以定义某处点云小于某个密度，既点云无效。计算每个点到其最近的k个点平均距离。则点云中所有点的距离应构成高斯分布。根据给定均值与方差，可剔除方差之外的点。即使方差之外的点是正确点，但是其太稀疏，带来的信息也是很少的。

特点：主要是根据密度去除离群点，对密度差异较大的离群点去除效果较好。

4）条件滤波器：条件滤波器通过设定滤波条件进行滤波，有点分段函数的味道，当点云在一定范围则留下，不在则舍弃。直通滤波器是一种较简单的条件滤波器。条件滤波器更像是一个不带有滤波核的工具。

5）半径滤波器：半径滤波器与统计滤波器相比更加简单粗暴。以某点为中心画一个圆计算落在该圆中点的数量，当数量大于给定值时，则保留该点，数量小于给定值则剔除该点。此算法运行速度快，依序迭代留下的点一定是最密集的，但是圆的半径和圆内点的数目都需要人工指定。

特点：主要还是用于去除离群点，在一定程度上可以用来筛选边缘点。

6）高斯滤波：高斯滤波是一种非线性滤波器，采用加权平均的方式。在指定域内的权重是根据欧式距离的高斯分布，通过权重加权平均的方式得到当前点的滤波后的点。

特点：高斯滤波平滑效果较好但是边缘角点也会被较大的平滑。

7）双边滤波：双边滤波是一种非线性滤波器，它可以达到保持边缘、降噪平滑的效果。一定程度上弥补了高斯滤波的缺点。双边滤波对高斯噪声效果比较好。

双边滤波从单纯的考虑空间域点的位置的高斯滤波上，又加上一个维度上的权重。在点云处理上，可以叫做为特征域，即当前点的法向量与临近点的法向量。通过改变两个域上的高斯滤波的方差来平衡平滑效果以及保持边缘的效果。

8）移动最小二乘法光滑滤波：移动最小二乘法光滑滤波思路很简单，就是根据点云，找到一个函数，这个函数有一系列的局部的函数组成（这个工作是通过移动最小二乘法完成的，可能需要一篇文章来解释移动最小二乘法），这个函数的特性是光滑的，然后将点投影到函数上，就完成了平滑的目的。

9）DoN算法（又叫基于点云频率的滤波方法）：DoN(Difference of Normal)，利用了多尺度空间的思想，算法的目的是在去除点云低频滤波（或者保留高频信息），低频信息（例如建筑物墙面，地面）往往会对分割产生干扰，高频信息（例如建筑物窗框，路面障碍锥）往往尺度上很小，直接采用基于临近信息的滤波器会将此类信息合并至墙面或路面中。算法如下：

1. 在小尺度上计算点云法线1
2. 在大尺度上计算点云法线2
3. 法线1-法线2
4. 滤去3中值较小的点(低频信息，较平坦的部分，如墙面地面等)
5. 欧式分割（将高频信息分开）

此算法的目的可以较好的分开高频信息和低频信息。

点云的频率：点云和图像一样，有可能也存在频率的概念。点云表达的是三维空间中的一种信息，这种信息本身并没有一一对应的函数值。故点云本身并没有在讲诉一种变化的信号。但点云存在某种空间关系。我们可以人为的指定点云空间中的一个点，基于此点来讨论点云在各个方向上所谓的频率。

在传统的信号处理中，高频信号一般指信号变化快，低频信号一般指信号变化缓慢。在图像处理中，高低频的概念被引申至不同方向上图像灰度的变化，傅里叶变换可以用于提取图像的周期成分滤除布纹噪声。

在点云处理中，定义：点云法线向量差为点云所表达的信号。换言之，如果某处点云曲率大，则点云表达的是一个变化的信号。如果点云曲率小，则其表达的是一个不变的信号。这和我们的直观感受也是相近的，地面曲率小，它表达的信息量也小；人的五官部分曲率大，其表达了整个Scan中最大的信息量。