【大数据分析与挖掘】KNN模型、朴素贝叶斯模型、SVM支持向量机模型学习笔记

KNN模型

KNN模型为有监督的学习算法，中文名为K最近邻算法。
k最近邻算法是数据挖掘中最简单的分类算法之一。

它属于“惰性”学习算法，其惰性在于不会从训练数据中学习判别函数（即模型），而是将模型的构建与未知数据的预测同时进行，靠记忆训练数据（仅仅保存训练样本）来完成预测任务。因此，在整个学习过程中，它付出的训练代价为零。

KNN既可以针对离散型变量做分类，又可以对连续型变量做回归预测。

核心思想

核心思想：比较已知y值的样本与未知y值样本的相似度，然后寻找最相似的k个样本用作未知样本的预测。

“最近”的度量就是样本之间的距离或相似性，如欧几里得距离(欧氏距离)、曼哈顿距离。
对于k最近邻分类，未知样本被分配到它的k个“最近邻”中的多数类中。

KNN模型的本质就是寻找k个最近样本，然后基于最近样本做“预测”。
对于离散型的因变量来说，从k个最近的已知类别样本中挑选出频率最高的类别用于未知样本的判断。
对于连续型的因变量来说，则是将k个最近的已知样本的均值用作未知样本的预测。

算法步骤

1.确定未知样本近邻的个数k值
2.根据某种度量样本间相似度的指标（如欧氏距离），将每一个未知类别样本的最近k个已知样本搜寻出来，形成一个个簇
3.对搜寻出来的已知样本进行投票，将各簇下类别最多的分类用作未知样本点的预测

度量方法

1.曼哈顿距离

2.欧式距离

朴素贝叶斯模型

朴素贝叶斯模型属于有监督的学习算法，可用于解决分类问题。

朴素贝叶斯分类器的实现思想非常简单，即通过已知类别的训练数据集，计算样本的先验概率所对应的类别作为样本的预测值。

朴素贝叶斯分类法的经典应用是文本分类。

优缺点

优点：
1.该算法在运算过程中简单而高效
2.其算法有古典概率的理论支撑，分类效率稳定
3.算法对缺失数据和异常数据不太敏感
缺点：
1.模型的判断结果依赖于先验概率，所以分类结果存在一定的错误率
2.对输入的自变量X要求具有相同的特征
3.模型的前提假设在实际应用中很难满足

核心假设

朴素贝叶斯分类器的核心假设为自变量之间是条件独立的。
该假设的主要目的是为了提高算法的运算效率，如果实际数据集中的自变量不满足独立性假设时，分类器的预测结果往往会产生错误。

做此假设是为了简化计算，并在此意义下成为“朴素”的

公式

条件概率：

全概率公式：

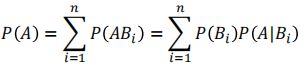
上面两者结合：：

C_i表示样本所属的某个类别，将计算所得的最大概率值P(C_i|X)对应的类别作为样本的最终分类，所得：
贝叶斯理论：

SVM支持向量机模型

SVM中文名为支持向量机，属于一种有监督的机器学习算法。
可用于离散型变量的分类和连续型变量的回归预测。

一般情况下，该算法相对于其他单一的分类算法(如Logistic回归、决策树、朴素贝叶斯、KNN等)会有更好的预测准确率
为啥呢❔主要是因为它可以将低维线性不可分的空间转换为高维的线性可分空间。
下面举个栗子来了解一哈啦
假设桌上有两种颜色的球，找到最大间隔的木棒位置，用一根木棍把他们分开，使得两边的球都离分隔他们的木棒足够远。
我们可以把这些球称为“数据”，把木棍称为“分类面”，找到最大间隔的木棒位置的过程称为“优化”。

但是如果球都混在一起呢‍♀️
假设桌上有两种颜色的球，大力一拍，球都飞到了空中，这时你非常灵敏的抓起一张纸片，插在这两类球的中间。
我们把拍桌子让球飞到空中的想象力称为“核映射”，在空中分隔球的纸片称为“分类超平面”（对于二维空间，则退化为一维直线）

这里插播一个概念
线性不可分的数据：线性不可分，可以理解为自变量和因变量之间的关系不是线性的。
将数据点从2维空间映射到3维空间中，使得数据线性可分。

手写体数字的识别是SVM的一个经典应用场景。
SVM模型最终所形成的分类器仅依赖一些支持向量

核心思想

SVM分类器实质上就是由某些支持向量构成的最大间隔的”超平面“，即分隔平面。
SVM模型的核心是构造一个”超平面“，并利用”超平面“将不同类别的数据做划分。
1.该算法的思想就是利用某些支持向量所构成的最大间隔的”超平面“，将不同类别的样本点进行划分。
2.不管样本点是线性可分的、近似线性可分的还是非线性可分的，都可以利用”超平面“将样本点以较高的准确度切割开来。
3.需要注意的是，如果样本点为非线性可分，就要借助于核函数技术，实现样本在核空间下完成线性可分的操作。