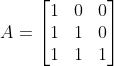C语言求矩阵的逆(高斯法)
初等变换法是常用的矩阵求逆方法之一
相对于伴随法,初等行变换法有着较低的时间复杂度,可以进行相对高维的矩阵运算,但同时也会损失一点点精度。
伴随法可参考之前的博客:C语言求矩阵的逆(伴随法)
目录
数学原理
矩阵的初等行变换
利用增广矩阵求逆
程序设计
整体代码
测试
数学原理
矩阵的初等行变换
矩阵的初等变换又分为矩阵的初等行变换和矩阵的初等列变换。矩阵的初等行变换和初等列变换统称为初等变换。另外:分块矩阵也可以定义初等变换。
定义:如果B可以由A经过一系列初等变换得到,则称矩阵A与B称为等价。
数域V上的矩阵具有以下三种行变换:
1)以V中一个非零的数,乘以矩阵的某一行
2)把矩阵的某一行的a倍加到另一行(a∈V)
3)互换矩阵中两行的位置
矩阵A通过以上三种行变换变成矩阵B,称为A→B
(注意:不要与行列式的行变换性质混淆)
利用增广矩阵求逆
如果想求矩阵A的逆,可以通过拼上一个单位E矩阵,形成A|E的增广矩阵,通过初等行变换使其成为E|B,B就是A的逆矩阵。
例如:
(1)形成A|E
(2)进行初等行变换,A|E→E|B
逆矩阵B则是
程序设计
整体流程:
1)判断传入指针是否为空,判断矩阵是否为方针
2)为增广矩阵、输出的逆矩阵开辟空间,并初始化为0
3)将原矩阵中的数据拷贝到增广矩阵中,并将增广矩阵右侧化为单位阵
4)对增广矩阵进行数据预处理,逐一找出每列最大的数,将每行都加上该行的值
5)逐列开始,将每列阶梯位置化为1,其他位置化为0
6)将增广矩阵右侧的逆矩阵拷贝到输入矩阵中,并释放增广矩阵内存
整体代码
#include
#include
#include
#include
double** Matrix_inver(double** src)
{
//step 1
//判断指针是否为空
if (src == NULL)exit(-1);
int i, j, k, row, col, n;
double** res, ** res2;//res为增广矩阵,res为输出的逆矩阵
int count = 0;
//判断矩阵维数
row = (double)_msize(src) / (double)sizeof(double*);
col = (double)_msize(*src) / (double)sizeof(double);
if (row != col)exit(-1);
//step 2
res = (double**)malloc(sizeof(double*) * row);
res2 = (double**)malloc(sizeof(double*) * row);
n = 2 * row;
for (i = 0; i < row; i++)
{
res[i] = (double*)malloc(sizeof(double) * n);
res2[i] = (double*)malloc(sizeof(double) * col);
memset(res[i], 0, sizeof(res[0][0]) * n);//初始化
memset(res2[i], 0, sizeof(res2[0][0]) * col);
}
//step 3
//进行数据拷贝
for (i = 0; i < row; i++)
{
memcpy(res[i], src[i], sizeof(res[0][0]) * n);
}
//将增广矩阵右侧变为单位阵
for (i = 0; i < row; i++)
{
for (j = col; j < n; j++)
{
if (i == (j - row))
res[i][j] = 1.0;
}
}
//step 4
//整理增广矩阵,每列元素找出最大那一行,加到其他行
for (j = 0; j < col; j++)
{
count = 0;
double Max = fabs(res[count][j]);//用绝对值比较
//默认第一行的数最大
for (i = 0; i < row; i++)
{
if (fabs(res[i][j]) > Max)
{
count = i;
Max = fabs(res[i][j]);
}
}
for (i = 0; i < row; i++)
{
if (i == count)continue;
for (k = 0; k < n; k++)
{
res[i][k] += res[count][k];
}
}
}
//step 5
for (j = 0; j < col; j++)
{
//阶梯处化成1
double a = 1.0 / res[j][j];
for (i = 0; i < n; i++)
{
res[j][i] *= a;
}
//将每列其他元素化0
for (i = 0; i < row; i++)
{
if (i == j)continue;
double b = res[i][j] / 1.0;
for (k = 0; k < n; k++)
{
res[i][k] += b * res[j][k] * (-1);
}
}
}
//step 6
//将逆矩阵部分拷贝到res2中
for (i = 0; i < row; i++)
{
memcpy(res2[i], res[i] + row, sizeof(res[0][0]) * row);
}
//必须释放res内存!
free(res);
return res2;
} 上述代码中:
函数传入的参数需是以malloc开辟的动态矩阵,如固定为二维数组,需自行更改
step 1: row = (double)_msize(src) / (double)sizeof(double*); col = (double)_msize(*src) / (double)sizeof(double); 为判断矩阵的维数;其中_msize为库函数,需要包含头文件
step 2: 增广矩阵的行数不变,列数是原来的2倍;对照该方法开辟矩阵空间,便可以理解step1中如何计算矩阵维数。
step 3: memset和memcpy都需要包含头文件
step 4:该步骤具有两层意义:1)相对程度上提高计算精度(因为计算机保存浮点数时有误差,增大计算时分母的值可提高计算精度)2)保证阶梯处的数都非0,方便计算
step 5:j代表从每列开始进行消0,i和k代表行和列;不要混淆j和k:j代表消零的大循环,k代表赋值的小循环。
step 6:res[i] + row代表只拷贝增广矩阵中逆矩阵部分,函数结束前必须释放增广矩阵的内存,否则将造成内存泄漏。
关于上述函数不太理解的地方可以参考之前发的判断矩阵维数和伴随法求逆矩阵
C语言动态内存部分可参考C语言动态内存管理
测试
相关测试函数(创建矩阵,初始化矩阵,打印矩阵)
double** MakeMat(int n)
{
int i = 0;
if (n <= 0)exit(-1);
double** res = (double**)malloc(sizeof(double*) * n);
if (res == NULL)exit(-1);
for (i = 0; i < n; i++)
{
res[i] = (double*)malloc(sizeof(double) * n);
}
return res;
}
void InitMat(double** src)
{
if (src == NULL)exit(-1);
int i, j, n;
n = (double)_msize(src) / (double)sizeof(double*);
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
src[i][j] = pow(i,j);
}
}
}
void print(double** src)
{
if (src == NULL)exit(-1);
putchar('\n');
int i, j, row,col;
row = (double)_msize(src) / (double)sizeof(double*);
col = (double)_msize(*src) / (double)sizeof(double);
for (i = 0; i < row; i++)
{
for (j = 0; j < col; j++)
{
printf("%9.4lf", src[i][j]);
}
putchar('\n');
}
}主函数测试:
int main()
{
int n = 5;
double** arr = MakeMat(n);
InitMat(arr);
double** res = Matrix_inver(arr);
printf("原矩阵:>");
print(arr);
printf("逆矩阵:>");
print(res);
return 0;
}打印结果:
如果矩阵接近奇异值,计算结果会不准确;如果矩阵秩亏,会输出无效值(nan)。