深度学习——“学习”过程中的更新方法

前言

本文将涉及的内容：
①寻找最优权重参数的最优方法、权重参数的初始值、超参数的设定方法。
②为了解决过拟合的问题，引入了 权值衰减、Dropout等正则化方法。
③Batch Normalization方法。

参数的更新

“学习”的目的是为了找到使得损失函数的值尽可能小的参数，这个过程叫做最优化。
前面通过使用参数的梯度，沿着梯度的方向更新参数，并重复这个过程，从而靠近最优参数，这个过程称为随机梯度下降法（SGD）。
下面将引入不同于 SGD其他的最优化方法。

————————————————————————————————
将数学式表示SGD：η表示学习率（事先约定）

从右边的值更新左边的值，将SGD 实现为一个python类。

class SGD:
	def __init__(self, lr=0.01):
		self.lr = lr
	def update(self, params, grads):
		for key in params.keys():
			params[key] -= self.lr * grads[key]

参数params和grads（与之前的神经网络的实现一样）是字典型变量，按params[‘W1’]、grads[‘W1’]的形式，分别保存了权重参数和它们的梯度。

学习过程的思路（伪代码）

network = TwoLayerNet(…)
optimizer = SGD()
for i in range(10000):
…
x_batch, t_batch = get_mini_batch(…) # mini-batch
grads = network.gradient(x_batch, t_batch)
params = network.params
optimizer.update(params, grads)
…

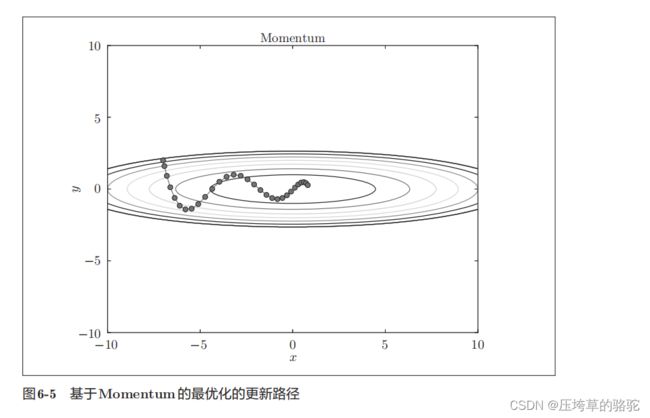
在后面将会介绍 最优化方法Momentum，它同样会实现成拥有update(params, grads)这个共同方法的形式。
只需要将optimizer = SGD()这一语句换成optimizer = Momentum()，就可以从SGD切换为Momentum。

很多深度学习框架都实现了各种最优化方法，并且提供了可以简单
切换这些方法的构造。

SGD 的缺点

以这个二元函数为例：



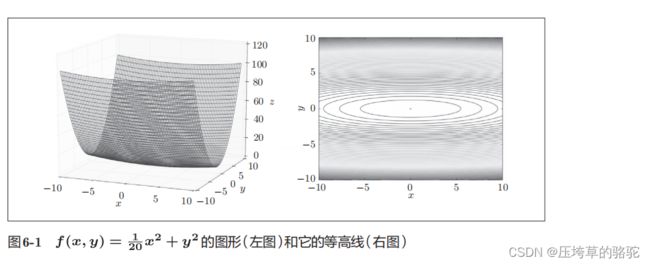
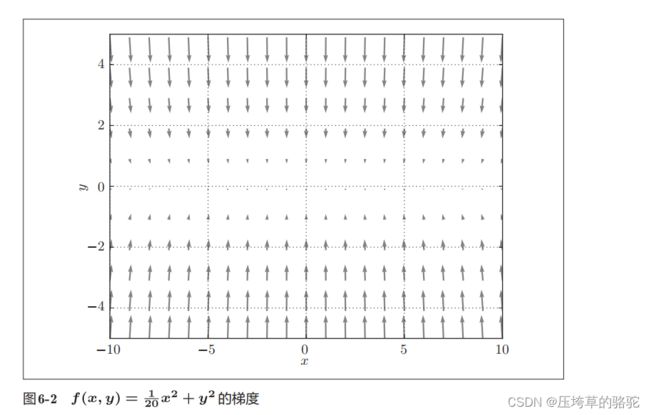
该梯度图的特点就是，在y轴上的坡度大，但是沿x轴坡度小，虽然在（0,0）处是最小值，但是梯度在很多地方并没有指向（0,0）

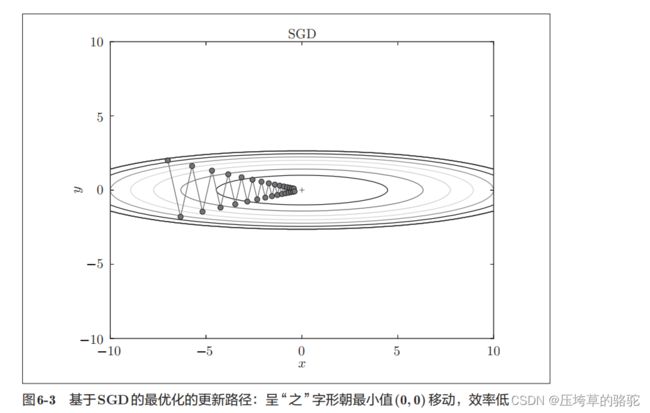
SGD的缺点是，如果函数的形状非均向（anisotropic），比如呈延伸状，搜索的路径就会非常低效。因此，我们需要比单纯朝梯度方向前进的SGD更聪明的方法。SGD低效的根本原因是，梯度的方向并没有指向最小值的方向。

如果函数的形状非均向（anisotropic），比如呈延伸状，搜索的路径就会非常低效
为了应对这种情况，介绍绍Momentum、AdaGrad、Adam这3种方法来取代SGD。

Momentum

用数学式表示Momentum方法，如下所示。

W表示要更新的权重参数,dL/dW表示损失函数关于W的梯度，η表示学习率。这里新出现了一个变量v，对应物理上的速度。αv这一项。在物体不受任何力时，该项承担使物体逐渐减速的任务（α设定为0.9之类的值），

class Momentum:
	def __init__(self, lr=0.01, momentum=0.9):
		self.lr = lr
		self.momentum = momentum
		self.v = None
		
	def update(self, params, grads):
		if self.v is None:
			self.v = {}
			for key, val in params.items():
				self.v[key] = np.zeros_like(val)
				
		for key in params.keys():
			self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
			params[key] += self.v[key]

梯度下降的路径更加“平滑”

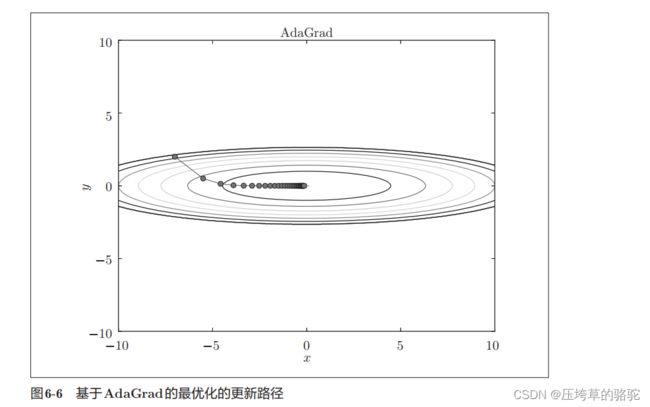
AdaGrad

学习率（数学式中记为η）的值很重要。学习率过小，会导致学习花费过多时间；反过来，学习率过大，则会导致学习发散而不能正确进行。
有一种被称为学习率衰减（learning rate decay）的方法，即随着学习的进行，使学习率逐渐减小。实际上，一开始“多”学，然后逐渐“少”学的方法。

数学式表示AdaGrad的更新方法。

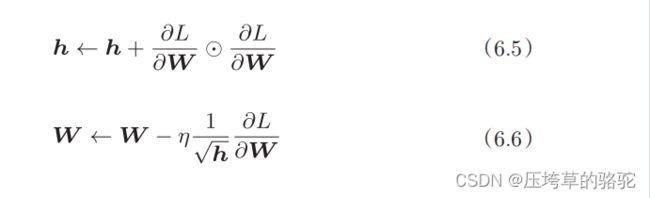
○表示对应矩阵元素的乘法

class AdaGrad:
	def __init__(self, lr=0.01):
		self.lr = lr
		self.h = None
	def update(self, params, grads):
		if self.h is None:
		self.h = {}
		for key, val in params.items():
			self.h[key] = np.zeros_like(val)
	for key in params.keys():
		self.h[key] += grads[key] * grads[key]
		#加上了微小值1e-7。这是为了防止当self.h[key]中有0时，将0用作除数的情况。
		params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

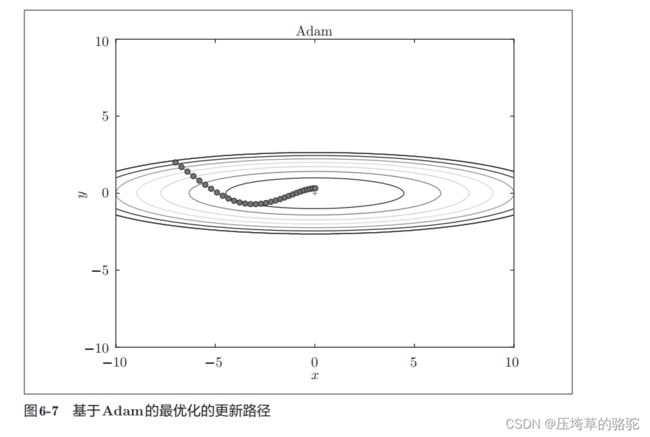
Adam

就是融合了Momentum和AdaGrad的方法。通过组合前面两个方法的优点,进行超参数的“偏置校正”也是Adam的特征。
Adam会设置 3个超参数。一个是学习率（论文中以α出现），另外两
个是一次momentum系数β1和二次momentum系数β2。

Adam会设置 3个超参数。一个是学习率（论文中以α出现），另外两
个是一次momentum系数β1和二次momentum系数β2。

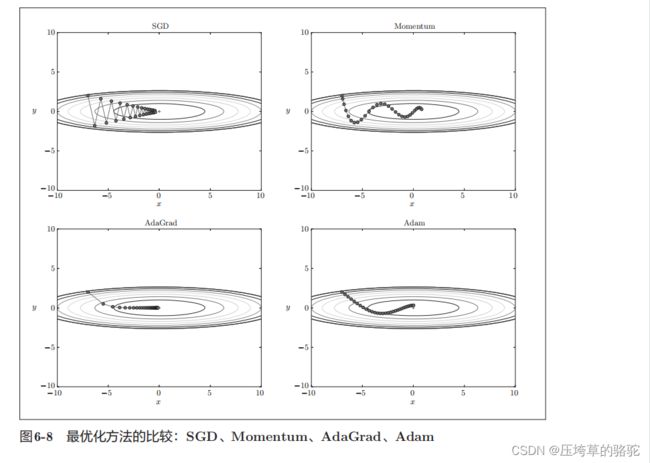
四种更新方法

基于MNIST数据集的更新方法的比较

以一个5层神经网络为对象，其中每层网络有100个神经元，激活函数使用ReLU。

import os
import sys
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import *


#0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000


#1:进行实验的设置==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
#optimizers['RMSprop'] = RMSprop()

networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []    

#2:开始训练==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    for key in optimizers.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizers[key].update(networks[key].params, grads)
    
        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)
    
    if i % 100 == 0:
        print( "===========" + "iteration:" + str(i) + "===========")
        for key in optimizers.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))


#3.绘制图形==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()

从结果的显示图可以看出，相较而言，AdaGrad的效果最好。

参考资料

《深度学习入门：基于Python的理论与实现》 斋藤康毅