LeNet实战（MNIST数据集）

关于LeNet理论部分请看LeNet框架详解

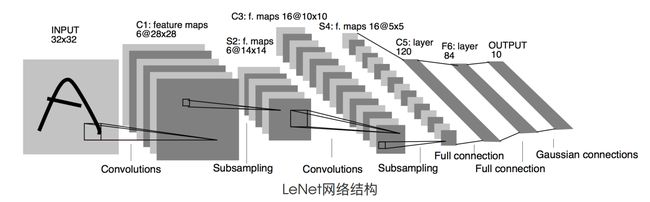
LeNet分为卷积层块和全连接层块两个部分。

卷积层块里的基本单位是卷积层后接最大池化层：卷积层用来识别图像里的空间模式，如线条和物体局部，之后的最大池化层则用来降低卷积层对位置的敏感性。在卷积层块中，每个卷积层都使用5×5的窗口，并在输出上使用sigmoid激活函数。第一个卷积层输出通道数为6，第二个卷积层输出通道数则增加到16。这是因为第二个卷积层比第一个卷积层的输入的高和宽要小，所以增加输出通道使两个卷积层的参数尺寸类似。卷积层块的两个最大池化层的窗口形状均为2×2，且步幅为2。

注意：我们代码以MNIST数据集进行训练和验证，MNIST数据集中图片大小是28*28，我们 LeNet框架详解中用的CIFAR数据集，其大小为32*32，注意区别！下图为以CIFAR数据集为输入的LeNet网络结构：

我们代码用MNIST数据集，所以在网络开始的第一个卷积层添加了padding=2，目的就是使得C1中每个feature map的大小为28*28，从而使后面的架构参数保持一致。

import torch
import torchvision as tv
import torchvision.transforms as transforms
import torch.nn as nn
import torch.optim as optim
import argparse

# 定义是否使用GPU
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
torch.backends.cudnn.enabled = False


# 定义网络结构，只是定义，没有运行顺序
class LeNet(nn.Module):
    def __init__(self):
        super(LeNet, self).__init__()
        # 构造网络有两种方式一个是seqential还有一个是module,前者在后者中也可以使用，这里使用的是sequential方式，将网络结构按顺序添加即可
        self.conv1 = nn.Sequential(  # input_size=(1*28*28)
            # 第一个卷积层，输入通道为1，输出通道为6，卷积核大小为5，步长为1，填充为2保证输入输出尺寸相同
            nn.Conv2d(1, 6, 5, 1, 2),  # padding=2保证输入输出尺寸相同 output_size=(6*28*28)
            # 激活函数,两个网络层之间加入，引入非线性

            nn.ReLU(),
            # 池化层，大小为2步长为2
            nn.MaxPool2d(kernel_size=2, stride=2),  # output_size=(6*14*14)
        )
        self.conv2 = nn.Sequential(  # input_size=(6*14*14)
            nn.Conv2d(6, 16, 5),  # output_size=(16*10*10)
            nn.ReLU(),
            nn.MaxPool2d(2, 2)  # output_size=(16*5*5)
        )
        # 全连接层，输入是16*5*5特征图，神经元数目120
        self.fc1 = nn.Sequential(  # input_size=(16*5*5)
            nn.Linear(16 * 5 * 5, 120),  # output_size=(120)
            nn.ReLU()
        )
        # 全连接层神经元数目输入为上一层的120，输出为84
        self.fc2 = nn.Sequential(  # input_size=(120)
            nn.Linear(120, 84),  # output_size=(84)
            nn.ReLU()
        )
        # 最后一层全连接层神经元数目10，与上一个全连接层同理
        self.fc3 = nn.Linear(84, 10)  # output_size=(10)

    # 定义前向传播过程，输入为x，也就是把前面定义的网络结构赋予了一个运行顺序
    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        # nn.Linear()的输入输出都是维度为一的值，所以要把多维度的tensor展平成一维
        x = x.view(x.size()[0], -1)
        x = self.fc1(x)
        x = self.fc2(x)
        x = self.fc3(x)
        return x  # 不要忘


# 使得我们能够手动输入命令行参数，就是让风格变得和Linux命令行差不多
parser = argparse.ArgumentParser()
parser.add_argument('--outf', default='./model/', help='folder to output images and model checkpoints')  # 模型保存路径
parser.add_argument('--net', default='./model/net.pth', help="path to netG (to continue training)")  # 模型加载路径
opt = parser.parse_args()

# 超参数设置
EPOCH = 8  # 遍历数据集次数
BATCH_SIZE = 64  # 批处理尺寸(batch_size)一次训练的样本数，相当于一次将64张图送入
LR = 0.001  # 学习率

# 定义数据预处理方式，将图片转换成张量的形式,因为后续的操作都是以张量形式进行的
transform = transforms.ToTensor()

# 下载数据集
# 定义训练数据集-60000张28*28图片
trainset = tv.datasets.MNIST(
    root='./data/',
    train=True,
    download=True,
    transform=transform)

# 定义训练批处理数据
trainloader = torch.utils.data.DataLoader(
    trainset,
    batch_size=BATCH_SIZE,
    shuffle=True,
)

# 定义测试数据集-10000张28*28图片
testset = tv.datasets.MNIST(
    root='./data/',
    train=False,
    download=True,
    transform=transform)

# 定义测试批处理数据
testloader = torch.utils.data.DataLoader(
    testset,
    batch_size=BATCH_SIZE,
    shuffle=False,
)

# 定义损失函数loss function 和优化方式（采用SGD）
net = LeNet().to(device)
criterion = nn.CrossEntropyLoss()  # 交叉熵损失函数，通常用于多分类问题上
optimizer = optim.SGD(net.parameters(), lr=LR, momentum=0.9)  # 梯度下降法求损失函数最小值

# 训练
if __name__ == "__main__":
    x, label = iter(trainloader).next()
    print('trainloader中一组数据的size:')
    print('x:', x.shape, 'label:', label.shape)
    print('trainset size:', len(trainset))

    x, label = iter(testloader).next()
    print('testloader中一组数据的size:')
    print('x:', x.shape, 'label:', label.shape)
    print('testset size:', len(testset))

    # 共进行8次遍历训练
    for epoch in range(EPOCH):
        sum_loss = 0.0
        # 读取下载的数据集
        for i, data in enumerate(trainloader):
            inputs, labels = data
            inputs, labels = inputs.to(device), labels.to(device)

            # 梯度清零
            optimizer.zero_grad()

            # forward + backward正向传播以及反向传播更新网络参数
            outputs = net(inputs)
            loss = criterion(outputs, labels)
            loss.backward()
            optimizer.step()

            # 每训练100个batch打印一次平均loss，基本上是一直减小的，一个epoch打印9次因为有6w张，一次batch64个，所以会
            # 取938个batch，最后一个batch不满64（只有32张）故每100次打印一次，共打印9次
            sum_loss += loss.item()
            if i % 100 == 99:
                print('[%d, %d] loss: %.03f'
                      % (epoch + 1, i + 1, sum_loss / 100))
                sum_loss = 0.0
        # 每跑完一次epoch测试一下准确率
        with torch.no_grad():
            correct = 0
            total = 0
            for i, data in enumerate(testloader):
                images, labels = data
                images, labels = images.to(device), labels.to(device)
                outputs = net(images)
                # 取得分最高的那个类
                _, predicted = torch.max(outputs.data, 1)
                total += labels.size(0)
                correct += (predicted == labels).sum()
            print('第%d个epoch的识别准确率为：%d%%  totaol:%d' % (epoch + 1, (100 * correct / total), total))
    # torch.save(net.state_dict(), '%s/net_%03d.pth' % (opt.outf, epoch + 1))