线性回归linear_model.LinearRegression

线性回归–监督学习

linear_model.LinearRegression

超参数

fit_intercept–是否计算截距，默认计算
normalize–是否标准化，默认不做
copy_x–是否对x肤质，如果为false，则经过中心化，标准化后，吧新数据覆盖到原数据上
n_job–计算时设置的任务个数

属性：

coef_:得到的feature的系数
intercept——截距，线性模型中的独立项
rank_：矩阵的秩
singular_ :矩阵的奇异值，尽在x为密集矩阵时有效

方法

fit
predict
score（模型评估，返回r^2系数，最优值为1，说明所有的数据都预测正确）
get_params()返回一个字典，键为参数名，值为估计器参数值
set_params 设置估计器的参数，可以修改参数重新训练

from sklearn.linear_model import LinearRegression
x=np.array([2,6])
y=np.array([3,5])
rfs=LinearRegression()
rfs.fit(x,y)
#报错：ValueError: Expected 2D array, got 1D array instead:array=[2 6].
#Reshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample

所以，线性回归的x一定是二维的矩阵

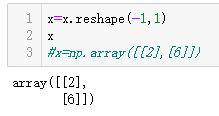
x=x.reshape(-1,1)
x
#x=np.array([[2],[6]])

#假设有第三个点，坐标为(3,6)
x2=np.array([[2],[3],[6]])
y2=np.array([3,6,5])
# 绘制三个点的散点图
plt.scatter(x2,y2,s=180,c='r')
# 利用线性回归模型拟合一条有均方误差最小的直线
lr_2=LinearRegression()
lr_2.fit(x2,y2)

y2_predict=lr_2.predict(x_test)
print(y2_predict)

print(lr_2.coef_,lr_2.intercept_)

#利用datasets升恒用于回归分析的数据集
from sklearn.datasets import make_regression
X_3,y_3=make_regression(n_samples=100,n_features=1)
plt.scatter(X_3,y_3)

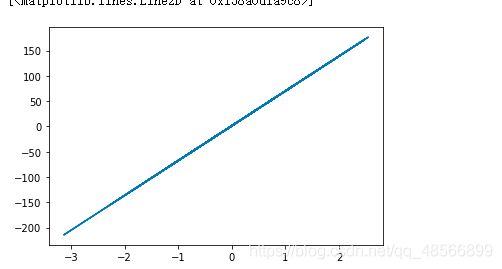
#绘制出拟合的直线
z=np.linspace(0,6,100)
z_predict=lr_2.predict(z.reshape(-1,1))
plt.plot(z,z_predict,lw=5,c='g')
plt.scatter(x2,y2,s=180,c='r')
#计算R方系数
lr_2.score(x2,y2)
#计算均方误差
from sklearn.metrics import mean_squared_error
mean_squared_error(y2,y2_predict)

利用make_regression 制作

n_samples:样本数
n_features:特征数
n_information:参与建模特征数
n_target：因变量个数
noise:噪音
bias：偏差
coef:是否输出coef标识
random_state

from sklearn.datasets import make_regression
X_3,y_3=make_regression(n_samples=100,n_features=1,noise=50,random_state=8)

plt.scatter(X_3,y_3)

rfs=LinearRegression()
rfs.fit(X_3,y_3)
k=rfs.coef_#斜率
b=rfs.intercept_
plt.plot(X_3,k*X_3+b)

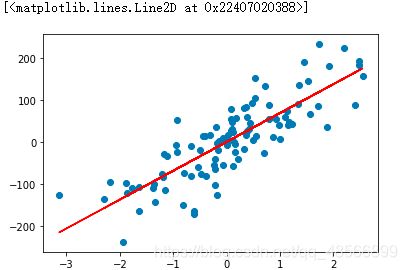
#利用线性回归进行拟合
X_3,y_3=make_regression(n_samples=100,n_features=1,noise=50,random_state=8)
plt.scatter(X_3,y_3)
rfs=LinearRegression()
rfs.fit(X_3,y_3)
y_3=rfs.predict(X_3)
plt.plot(X_3,y_3,'r-')

糖尿病数据集的线性回归

from sklearn.datasets import load_diabetes
diabetes=load_diabetes()
print(diabetes['DESCR'])

X=diabetes.data#特征变量
y=diabetes.target#因变量
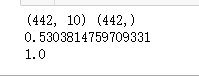
print(X.shape,y.shape)
#划分训练集测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=8)
lr=LinearRegression().fit(X_train,y_train)
y_test=lr.predict(X_test)
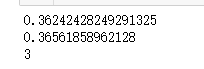
print(lr.score(X_train,y_train))
print(lr.score(X_test,y_test))

from sklearn import datasets
X,y = datasets.load_diabetes(return_X_y=True)

岭回归实践

超参数

alpha
fit_intercept:截距
copy_X:若为true，将复制x，否则，可能被覆盖
max_iter:共振梯度求解器的最大迭代次数，若为none，则为默认值，不同silver的默认值不同，对于’sparse_cg’/'lsgr’求解器，默认值由scipy.sparse.linalg确定。对于’sag’求解器，默认值为1000
normalize:如果为真，则回归x在回归之前被归一化。

from sklearn.linear_model import Ridge
ridge=Ridge()
from sklearn.datasets import load_diabetes
diabetes=load_diabetes()
X=diabetes.data
y=diabetes.target
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=8)
ridge.fit(X_train,y_train)
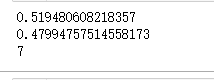
print(ridge.score(X_train,y_train))
print(ridge.score(X_test,y_test))

岭回归的参数调节

# 正则化系数alpha=10
ridge10=Ridge(alpha=10).fit(X_train,y_train)
print(ridge10.score(X_train,y_train))
print(ridge10.score(X_test,y_test))

# 正则化系数alpha=0.1
ridge01=Ridge(alpha=0.1).fit(X_train,y_train)
print(ridge01.score(X_train,y_train))
print(ridge01.score(X_test,y_test))

# 模型系数的可视化比较
plt.plot(ridge.coef_,'s',label='ridge alpha=1')
plt.plot(ridge10.coef_,label='ridge alpha=10')
plt.plot(ridge01.coef_,label='ridge alpha=0.1')
plt.xlabel('系数序号')
plt.ylabel('系数量级')
plt.hlines(0,0,len(lr.coef_))
plt.legend(loc='best')
plt.grid(linestyle=':')
plt.rcParams['font.sans-serif']=['SimHei','Times New Roman']
plt.rcParams['axes.unicode_minus']=False

绘制学习曲线，取固定的alpha值，改变训练集的数据量

from sklearn.model_selection import learning_curve,KFold

def plot_learning_curve(est,X,y):
    training_set_size,train_scores,test_scores=learning_curve(est,X,y,train_sizes=np.linspace(.1,1,20),cv=KFold(20,shuffle=True,random_state=1))
    eatimator_name=est._class_._name_
    line=plt.plot(training_set_size,train_scores.mean(axis=1),'--',label='training'+estimator_name)
    plt.plot(training_set_size,test_scores.mean(axis=1),'-',label='test'+estimator_name,c=line[0].get_color())
    plt.xlabel('training set size')
    plt.ylabel('score')
    plt.ylim(0,1.1)
plot_learning_curve(Ridge(alpha=1),X,y)
plot_learning_curve(Ridge(LinearRegressiong(),X,y))
plt.legend(loc=(0,1.05),ncol=2,fontsize=11)

plt.grid(linestyle=':')

Lasso回归实践

from sklearn.linear_model import Lasso
lasso=Lasso()
lasso.fit(X_train,y_train)
print(lasso.score(X_train,y_train))
print(lasso.score(X_test,y_test))
print(np.sum(lasso.coef_!=0))#套索回归使用的特征数

lasso=Lasso(max_iter=100000)#增加最大迭代次数的默认设置，默认max_iter=1000
lasso.fit(X_train,y_train)
print(lasso.score(X_train,y_train))
print(lasso.score(X_test,y_test))
#特征选择
print(np.sum(lasso.coef_!=0))

lasso=Lasso(alpha=0.1,max_iter=100000)
#增加最大迭代次数的默认设置，默认max_iter=1000
#回归调整alpha
lasso.fit(X_train,y_train)
print(lasso.score(X_train,y_train))
print(lasso.score(X_test,y_test))
#特征选择
print(np.sum(lasso.coef_!=0))

lasso=Lasso(alpha=0.0001,max_iter=100000)
#增加最大迭代次数的默认设置，默认max_iter=1000
#回归调整alpha
lasso.fit(X_train,y_train)
print(lasso.score(X_train,y_train))
print(lasso.score(X_test,y_test))
#特征选择
print(np.sum(lasso.coef_!=0))

plt.plot(ridge.coef_,'s',label='ridge alpha=1')
plt.plot(ridge10.coef_,'^',label='ridge alpha=10')
plt.plot(ridge.coef_,'v',label='ridge alpha=0.1')
plt.plot(lr.coef_,'o',label='linear regression')

plt.plot(lasso.coef_,'D',label='lasso alpha=1')
plt.plot(lasso01,coef_,'H',label='lasso alpha=0.1')
plt.plot(lasso00001,coef_,'p',label='lasso alpha=0.0001')
plt.plot(ridge01,coef_,'<',label='ridge alpha=0.1')
plt.xlabel('系数序号')
plt.ylabel('系数量级')
plt(hlines(0,0,len(lr.coef_)))
plt.legend(loc='best')
plt.grid(linestyle=':')