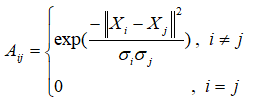相似度矩阵的几种构造方式（附代码）

标题
  在谱聚类中，常将数据看做空间上的点，点之间用边连接起来，构造无向权重图$\mathbf{G}=(\mathbf{V},\mathbf{E})$，其中$\mathbf{V}=\{v_1,v_2,...,v_n\}$为定点集合，E为边集合。对任意一个顶点Vi，度di表示与它相连的所有边权重之和，W(i,j)表示Vi和Vj之间的边权重，那么  那么对于n个顶点，可构造$n\ast n$的度矩阵D=diag(d1,d2,…,dn)。同时，利用所有顶点之间的权重，得邻接矩阵(相似度矩阵)W。
  常见的邻接矩阵W的构造方法有3种，分别是$\epsilon$-邻近、k-邻近、全连接法。
  本文主要基于高斯核的全连接法构造邻接矩阵W。$\epsilon$-邻近、k-邻近的具体构造方法见这篇文章。

---

  已知$\mathbf{X}=[{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_n]\in {\mathbb{R}}^{n\times d}$，使用高斯核RBF作为核函数，有：
其中，$\sigma$表示数据点的邻域宽度。

  目前，对于$\sigma$有两种不同输入，一种由人工选取，作为固定值（single scale parameter，单值参数）输入，另一种由self-tuning算法提出的自动选取方法，即$\sigma$是一个变量（local scaling parameter，局部值），对于不同的样本点，$\sigma$不同。

当$\sigma$是单值（single scale）

计算公式：

① 纯手工计算

% 输入X，sigma
[row,col] = size(X);
W = zeros(row,row);
index_all = zeros(row,row);
for i = 1:row                   % 全连接构造相似度矩阵W
    for j=1:row
        if i ~= j
            W(i,j) = exp((-sum((X(i,:)-X(j,:)).^2))/(2*sigma.^2));
        end
    end
end
Affinity = W;  

② 蔡登的constructW.m

完整代码见：github
注意，要使用全连接图，option.k = 0.
运行结果 W 与‘’① 纯手工计算‘’结果应一致.（W与后文的邻接矩阵/亲和矩阵A 相同）

function W = constructW(fea,options)
%	Usage:
%	W = constructW(fea,options)
%
%	fea: Rows of vectors of data points. Each row is x_i
%   options: Struct value in Matlab. The fields in options that can be set:
%                  
%           NeighborMode -  Indicates how to construct the graph. Choices
%                           are: [Default 'KNN']
%                'KNN'            -  k = 0
%                                       Complete graph
%                                    k > 0
%                                      Put an edge between two nodes if and
%                                      only if they are among the k nearst
%                                      neighbors of each other. You are
%                                      required to provide the parameter k in
%                                      the options. Default k=5.
%               'Supervised'      -  k = 0
%                                       Put an edge between two nodes if and
%                                       only if they belong to same class. 
%                                    k > 0
%                                       Put an edge between two nodes if
%                                       they belong to same class and they
%                                       are among the k nearst neighbors of
%                                       each other. 
%                                    Default: k=0
%                                   You are required to provide the label
%                                   information gnd in the options.
%                                              
%           WeightMode   -  Indicates how to assign weights for each edge
%                           in the graph. Choices are:
%               'Binary'       - 0-1 weighting. Every edge receiveds weight
%                                of 1. 
%               'HeatKernel'   - If nodes i and j are connected, put weight
%                                W_ij = exp(-norm(x_i - x_j)/2t^2). You are 
%                                required to provide the parameter t. [Default One]
%               'Cosine'       - If nodes i and j are connected, put weight
%                                cosine(x_i,x_j). 
%               
%            k         -   The parameter needed under 'KNN' NeighborMode.
%                          Default will be 5.
%            gnd       -   The parameter needed under 'Supervised'
%                          NeighborMode.  Colunm vector of the label
%                          information for each data point.
%            bLDA      -   0 or 1. Only effective under 'Supervised'
%                          NeighborMode. If 1, the graph will be constructed
%                          to make LPP exactly same as LDA. Default will be
%                          0. 
%            t         -   The parameter needed under 'HeatKernel'
%                          WeightMode. Default will be 1
%         bNormalized  -   0 or 1. Only effective under 'Cosine' WeightMode.
%                          Indicates whether the fea are already be
%                          normalized to 1. Default will be 0
%      bSelfConnected  -   0 or 1. Indicates whether W(i,i) == 1. Default 0
%                          if 'Supervised' NeighborMode & bLDA == 1,
%                          bSelfConnected will always be 1. Default 0.
%            bTrueKNN  -   0 or 1. If 1, will construct a truly kNN graph
%                          (Not symmetric!). Default will be 0. Only valid
%                          for 'KNN' NeighborMode
%    For more details about the different ways to construct the W, please
%    refer:
%       Deng Cai, Xiaofei He and Jiawei Han, "Document Clustering Using
%       Locality Preserving Indexing" IEEE TKDE, Dec. 2005.
%    
%
%    Written by Deng Cai (dengcai2 AT cs.uiuc.edu), April/2004, Feb/2006,
%                                             May/2007

options = [];
options.NeighborMode = 'KNN';
options.k = 0;                 % 全连接图
    
options.WeightMode = 'HeatKernel';
options.t = 1;                  % Kernel sigma，要与‘① 纯手工计算’中设定的一致
W = constructW(X,options);
Affinity = full(W);

 

当$\sigma$是局部值（local scaling parameter）

  计算公式：

  注意，指数部分的分母没有1/2

  其中，${\mathbf{X}}_{\mathbf{i}\mathbf{K}}$是${\mathbf{X}}_{\mathbf{i}}$样本点的第K个邻近点(在距离上)。
 
  该思想源自作者Lihi Zelnik-Manor的论文《Self-Tuning Spectral Clustering》中的Section 2，论文的代码包在我的github上：ZPclustering.rar。

① “self-tuning spectral clustering”论文代码

核心代码文件：dist2aff.cpp / scale_dist.cpp / segment_image.m / test1.m

dist2aff.cpp ：输入 distmatrix，X的欧式平方距离矩阵
                    sigma ， 高斯核函数的参数
               输出 ： A ，sigle scale下的邻接矩阵，公式exp(-distmatrix./(sigma*sigma)) 

scale_dist.cpp ：输入 distmatrix，X的欧式平方距离矩阵
                      k， sigma（i）取决于样本及其第k个邻近点的欧氏距离sigma(i)=||Xi-XiK||
               输出 ： A ，local scale下的邻接矩阵，公式exp(-distmatrix(i,j)./(sigma(i)*sigma(j)))
               
scale_dist.cpp代码内容补充解释：
LS(i,j) = sigma(i)*sigma(j)
D(i,j) = ||Xi-Xj||^2
D_LS(i,j) = ( ||Xi-Xj||^2 )/ (sigma(i)*sigma(j)) = LS(i,j)/D(i,j)
A_LS(i,j) = exp{( ||Xi-Xj||^2 )/ (sigma(i)*sigma(j))} = exp(D_LS(i,j))

（以下若遇到解决错误使用mex未找到支持的编译器或SDK问题，根据Matlab提示网站查看details，下载sdk 7.1 和.Net 4.0等操作，部分安装指导：参考博客1的3.1部分、参考博客2，若编译成功显示如：）
我整理的相似度矩阵构造代码：main_Run.m,如下：

mex dist2aff.cpp  ;
mex scale_dist.cpp ;

%%%%%%%%%%%%%%%%% Build affinity matrices
% the equation of kernel function is exp(-dist(i,j)/sigma1*simga2),for
% single-scale affinity construction,sigma1 equal to sigma2 ,while for
% automatic-selftuning affinity construction ,the value of sigma1,2 is 
% dependent of the the k'th neughbor of Xi.

% input：X ，scale
% output：A ， A_LS
% 
%***** Ayla Huang ****


scale = 0.1;                 %% parameter sigma in kernel
D = dist2(X,X);              %% Euclidean  square distance
A = exp(-D/(scale^2));       %% Standard affinity matrix (single scale)

k = 5;                       %% the number of neighbor, the k'th neighbor for selftuning
[D_LS,A_LS,LS] = scale_dist(D,k); %% Locally scaled affinity matrix (automatic selftuning)                    
clear D_LS; clear LS;
    
% Zero out diagonal
% the diag-element in A and A_LS is 1 ,now turn it to zero.
ZERO_DIAG = ~eye(size(X,1));
A = A.*ZERO_DIAG;
A_LS = A_LS.*ZERO_DIAG;

②自编代码selftuning2.m

原理相同，用纯Matlab实现。
注意A(i,j) = exp((-sum((X(i,:)-X(j,:)).^2))/(sigma(i)*sigma(j)));
运行结果 A 与‘’① “self-tuning spectral clustering”论文代码‘’结果一致.

function [A,An] = selftuning2(X,k)

%% load Data
% X = getData(data_name);

%% construct affinity matrix A

[n,~]=size(X);
% 全连接欧式距离矩阵dis_all
dis_all = L2_distance_1(X',X'); % 平方距离
dis_all(find(dis_all<0)) = 0;
dis_all = sqrt(dis_all);

% 使用KNN计算欧式距离最近的 '第k个'点sigma，保留n个样本的第k近距离结果sigma(n,1)
[dumb,idx] = sort(dis_all, 2); % sort each row
index=idx(:,k+1);

sigma = zeros(n,1);
for i=1:n
    sigma(i)=sqrt(sum((X(i,:)-X(index(i),:)).^2));
end

%构造selftuning下的affinity矩阵A
A=zeros(n,n);
for i = 1:n                   
    for j=1:n
        if i ~= j
            A(i,j) = exp((-sum((X(i,:)-X(j,:)).^2))/(sigma(i)*sigma(j)));
        end
    end
end

D = diag(sum(A,2));
Dn1 = D^(-0.5);
An = Dn1*A*Dn1; %前c个最大,An是拉普拉斯矩阵
clear Dn;
An = max(An,An');


function d = L2_distance_1(a,b)
% compute squared Euclidean distance
% ||A-B||^2 = ||A||^2 + ||B||^2 - 2*A'*B
% a,b: two matrices. each column is a data
% d:   distance matrix of a and b

if (size(a,1) == 1)
  a = [a; zeros(1,size(a,2))]; 
  b = [b; zeros(1,size(b,2))]; 
end

aa=sum(a.*a); bb=sum(b.*b); ab=a'*b; 
d = repmat(aa',[1 size(bb,2)]) + repmat(bb,[size(aa,2) 1]) - 2*ab;

d = real(d);
d = max(d,0);