pytorch学习笔记二：动态图、自动求导及逻辑回归

一、计算图

计算图是描述运算的有向无环图，有两个主要的元素：节点（Node）和边（Edge），节点表示数据，如向量，矩阵，张量。边表示运算，如加减乘除等。
用计算图表示： $y=\left(x+w\right)\ast \left(w+1\right)$ ,如下所示：

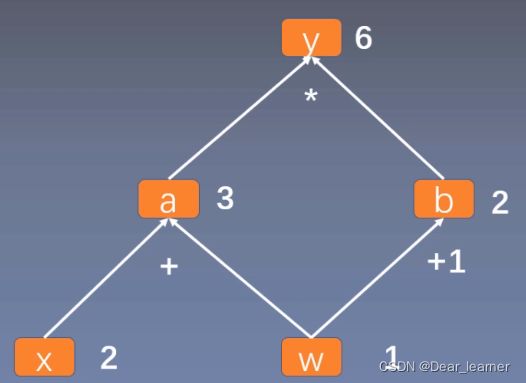
从上面可以看出y = a × b，而a = w + x, b = w + 1，只要给出x和w的值，即可根据计算图得出y的值。

计算图与梯度求导
求y对w的导数，根据求导规则，如下：

体现到计算图中，就是根节点 y 到叶子节点 w 有两条路径 y -> a -> w和y ->b -> w。根节点依次对每条路径的叶子节点求导，一直到叶子节点w，最后把每条路径的导数相加即可。

x = torch.tensor([2.], requires_grad=True)
w = torch.tensor([1.], requires_grad=True)

# y = (x + w) * (w + 1)
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)

#y求导
y.backward()
#w的梯度就是y对w的求导
print(w.grad)

###result
tensor([5.])

在tensor中包含一个is_leaf(叶子节点)属性，叶子节点就是用户创建的节点，在上面的例子中，x 和 w 是叶子节点，其他所有节点都依赖于叶子节点。叶子节点的概念主要是为了节省内存，在计算图中的一轮反向传播结束之后，非叶子节点的梯度是会被释放的。

#查看是否是叶子节点
print(w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf)

###result
True True False False

#查看梯度
print(w.grad, x.grad, a.grad, b.grad, y.grad)

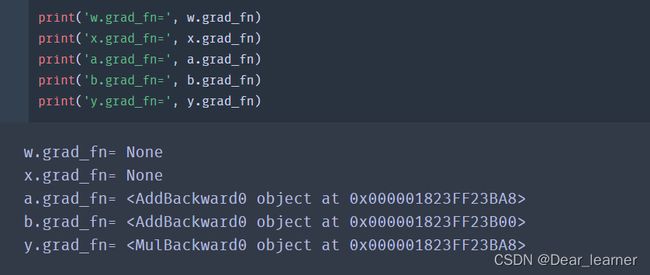
输出结果：

只有叶子节点的梯度保留了下来，而非叶子的梯度为空，如果在反向传播之后仍需要保留非叶子节点的梯度，可以对节点使用retain_grad()方法。
grad_fn：记录创建该张量时所用的方法（函数），记录这个方法主要是用于【梯度的求导】

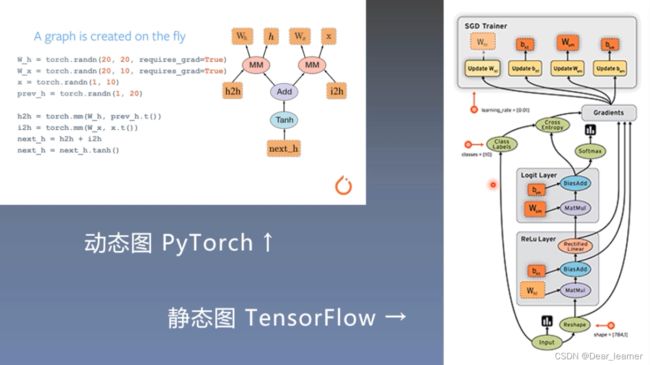
二、动态图机制

pytroch采用的是动态图机制，而tensorflow采用的是静态图机制

静态图是先搭建，后运算
动态图是运算和搭建同时进行，也就是可以先计算前面节点的值，再根据这些值搭建后面的计算图。优点是灵活，易调节，易调试。

三、自动求导机制

pytorch的自动求导机制是torch.autograd.backward()方法，功能是自动求取梯度

torch.autograd.backward(
    tensors: Union[torch.Tensor, Sequence[torch.Tensor]],
    grad_tensors: Union[torch.Tensor, Sequence[torch.Tensor], NoneType] = None,
    retain_graph: Union[bool, NoneType] = None,
    create_graph: bool = False,
    grad_variables: Union[torch.Tensor, Sequence[torch.Tensor], NoneType] = None,
    inputs: Union[torch.Tensor, Sequence[torch.Tensor], NoneType] = None,
) -> None

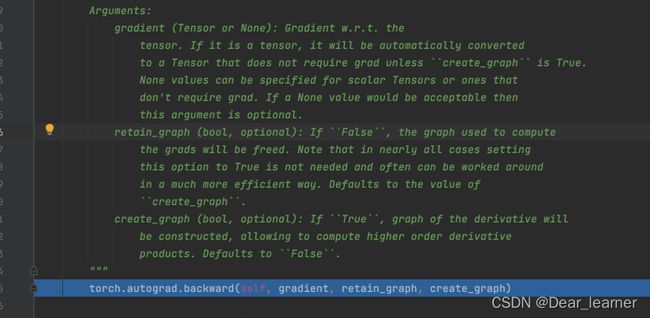
● tensor:表示用于求导的张量，如loss，
● grad_tensor: 设置梯度权重，在计算矩阵的梯度时会用到，也是一个tensor，shape和前面的tensor保持一致
● retain_graph:表示保存计算图，由于pytorch采用了动态图机制，在每一次反向传播之后，计算图都会被释放掉。如果不想释放，就设置这个参数为True
● create_graph:创建导数计算图，用于高阶求导

在上面对y求导 y.backward() 处设置断点，进行debug，可以看出调用的是 torch.autograd.backward() 方法,所以 torch.autograd.backward(y)==y.backward()

在每一次反向传播之后，计算图会释放掉，如果想要使用计算图，可以设置参数retain_graph=True

x = torch.tensor([2.], requires_grad=True)
w = torch.tensor([1.], requires_grad=True)

# y = (x + w) * (w + 1)
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)

#y求导
y.backward()
#w的梯度就是y对w的求导
# print(w.grad)

y.backward()

输出结果：

设置梯度权重

x = torch.tensor([2.], requires_grad=True)
w = torch.tensor([1.], requires_grad=True)

# y = (x + w) * (w + 1)
a = torch.add(w, x)
b = torch.add(w, 1)

y0 = torch.mul(a, b)
y1 = torch.add(a, b)

loss = torch.cat([y0, y1], dim=0)
grad_tensor = torch.tensor([1., 1.])

loss.backward(gradient=grad_tensor)
print(w.grad)

# result
tensor([7.])

torch.autograd.grad()这个方法的功能也是求梯度，可以实现高阶的求导。

torch.autograd.grad(
    outputs: Union[torch.Tensor, Sequence[torch.Tensor]],
    inputs: Union[torch.Tensor, Sequence[torch.Tensor]],
    grad_outputs: Union[torch.Tensor, Sequence[torch.Tensor], NoneType] = None,
    retain_graph: Union[bool, NoneType] = None,
    create_graph: bool = False,
    only_inputs: bool = True,
    allow_unused: bool = False,
) -> Tuple[torch.Tensor, ...]

• outputs：用于求导的张量；
• inputs: 需要梯度的张量；
• create_graph:创建导数计算图，用于高阶求导
• retain_graph:保存计算图
• grad_outputs:多梯度权重

使用autograd需要注意：
● 梯度不自动清零；
● 依赖于叶子结点的结点，默认requires_grad=True;
● 叶子结点不可执行in-place;
示例如下：

x = torch.tensor([2.], requires_grad=True)
w = torch.tensor([1.], requires_grad=True)

for i in range(4):
    a = torch.add(w, x)
    b = torch.add(w, 1)
    y = torch.mul(a, b)

    y.backward()
    print(w.grad)

    # w.grad.zero_()
# 梯度不清零，运算结果
tensor([5.])
tensor([10.])
tensor([15.])
tensor([20.])

#梯度清零的运算结果
tensor([5.])
tensor([5.])
tensor([5.])
tensor([5.])

print(a.requires_grad, b.requires_grad, y.requires_grad)
#result
True True True

x = torch.tensor([2.], requires_grad=True)
w = torch.tensor([1.], requires_grad=True)

# y = (x + w) * (w + 1)
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)

w.add_(1)
y.backward()
print(w.grad)
#运行结果会报错
#这是因为在前向传播时已经记录了w的地址，在反向传播时需要利用这个地址来进行求导，若对w进行in-place操作
#会改变w的地址，这就会导致反向传播过程出错。

运行结果：

下面从具体的实例来理解上面两个求导的方法
一个简单的求导例子是：$y=\left(x+1\right)\ast \left(x+2\right)$ ，计算$\frac{\partial y}{\partial x}$，假设给定 x=2
先画出计算图


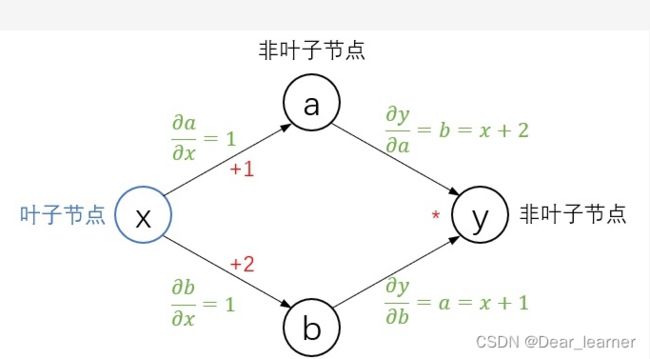
使用backward()

x = torch.tensor(2., requires_grad=True)

a = torch.add(x, 1)
b = torch.add(x, 2)
y = torch.mul(a, b)

y.backward()
print(x.grad)

###result
tensor(7.)

#查看一下这几个tensor的属性
print('requires_grad:', x.requires_grad, a.requires_grad, b.requires_grad, y.requires_grad)
print('is_leaf:', x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)
print('grad:', x.grad, a.grad, b.grad, y.grad)

###result
requires_grad: True True True True
is_leaf: True False False False
grad: tensor(7.) None None None

使用backward（）计算tensor的梯度时，并不是所有的tensor都能计算其梯度，只能满足这几个条件的tensor：
1、类型为叶子节点；
2、requires_grad=True；
3、依赖该tensor的requires_grad=True的tensor。
所有满足条件的变量梯度会自动保存到grad属性中。

使用autograd.grad()

x = torch.tensor(2., requires_grad=True)

a = torch.add(x, 1)
b = torch.add(x, 2)
y = torch.mul(a, b)

grad = torch.autograd.grad(outputs=y, inputs=x)
print(grad[0])
print(grad)
####result
tensor(7.)
(tensor(7.),)

因为指定了输出y，输入x，所以返回值就是 $\frac{\partial y}{\partial x}$ 这一梯度，完整的返回值其实是一个元组，保留第一个元素。

高阶求导的例子：$z=x^2\ast y$，计算 $\frac{\partial z}{\partial x}$， $\frac{\partial z}{\partial y}$，$\frac{\partial z^2}{\partial x^2}$，假设给定 x = 2，y = 3

x = torch.tensor(2., requires_grad=True)
y = torch.tensor(3., requires_grad=True)

z = x * x * y
z.backward()
print('x_grad:', x.grad)
print('y_grad:', y.grad)
###result
x_grad: tensor(12.)
y_grad: tensor(4.)

x = torch.tensor(2.).requires_grad_()
y = torch.tensor(3.).requires_grad_()

z = x * x * y

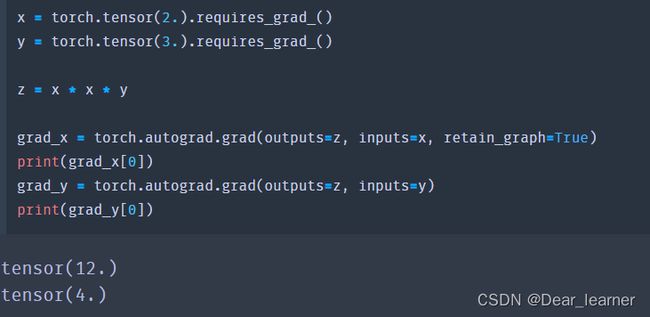
grad_x = torch.autograd.grad(outputs=z, inputs=x)
grad_y = torch.autograd.grad(outputs=z, inputs=y)
print(grad_x[0])
print(grad_y[0])

输出结果：

在对y求导时报错，是因为在backward()和autograd.grad在计算一次梯度之后就被释放了，如果想要保留，就要用retain_graph=True,在计算完x的梯度后保留计算图，

如何进行高阶求导，理论上是由上面的grad_x再对x求导

x = torch.tensor(2.).requires_grad_()
y = torch.tensor(3.).requires_grad_()

z = x * x * y

grad_x = torch.autograd.grad(outputs=z, inputs=x, retain_graph=True)
grad_xx = torch.autograd.grad(outputs=grad_x, inputs=x)
print(grad_xx[0])

输出结果：

虽然retain_graph=True保留了计算图和中间变量梯度， 但没有保存grad_x的运算方式，需要使用creat_graph=True在保留原图的基础上再建立额外的求导计算图，也就是会把 $\frac{\partial z}{\partial x}=2xy$ 这样的运算存下来

grad_xx这里也可以直接用backward()，相当于直接从 $\frac{\partial z}{\partial x}=2xy$ 开始回传

x = torch.tensor(2.).requires_grad_()
y = torch.tensor(3.).requires_grad_()

z = x * x * y

grad_x = torch.autograd.grad(outputs=z, inputs=x, create_graph=True)
grad_x[0].backward()
print(x.grad)
#result
tensor(6.)

从上面的求导看出，是从x.grad开始回传，下面是从z开始回传，得到的结果是18，这是为什么呢？
因为第一次回传时，x的梯度时12，第二次梯度回传时，x的梯度时6，两次的梯度进行了累加。这是因为pytorch使用backward（）时默认会累加梯度，这时需要手动的把梯度清零

将梯度清零

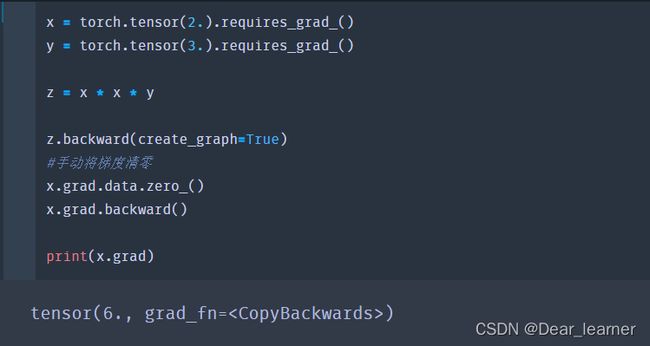
在上面的示例中都是对标量进行求导，如果不是标量呢

x = torch.tensor([1., 2.]).requires_grad_()
y = x + 1

y.backward()
print(x.grad)

报错了，因为只能标量对标量，标量对向量求梯度， x 可以是标量或者向量，但 y 只能是标量；所以只需要先将 y 转变为标量，对分别求导没影响的就是求和。
此时：

x = torch.tensor([1., 2.]).requires_grad_()
y = x * x

y.sum().backward()
print(x.grad)
###result
tensor([2., 4.])

求导计算雅克比矩阵：$y=\left[y_1,y_2\right]$ 是一个向量
$J=\left[\frac{\partial y}{\partial x1},\frac{\partial y}{\partial x2}\right]=\left[\begin{array}{cc}\frac{\partial y1}{\partial x1}& \frac{\partial y1}{\partial x2}\\ \frac{\partial y2}{\partial x1}& \frac{\partial y2}{\partial x2}\end{array}\right]$，希望最终的结果是 $\left[\frac{\partial y1}{\partial x1},\frac{\partial y2}{\partial x2}\right]$
注意到 $\frac{\partial y1}{\partial x2}$ ，$\frac{\partial y2}{\partial x1}$ 是0，所以

x = torch.tensor([1., 2.]).requires_grad_()
y = x * x

y.backward(torch.ones_like(x))
print(x.grad)
###result
tensor([2., 4.])

也可以使用autograd。上面和这里的torch.ones_like(x) 位置指的就是雅可比矩阵右乘的那个向量

x = torch.tensor([1., 2.]).requires_grad_()
y = x * x

grad_x = torch.autograd.grad(outputs=y, inputs=x, grad_outputs=torch.ones_like(x))
print(grad_x[0])

##或者
x = torch.tensor([1., 2.]).requires_grad_()
y = x * x

grad_x = torch.autograd.grad(outputs=y.sum(), inputs=x)

梯度清零
Pytorch的自动求导机制的梯度时累加的，所以每一次反向传播之后梯度要清零

x.grad.zero_()

###在神经网络中，需要执行
optimizer.zero_grad()

detach() 切断
假设有模型A和模型B，我们需要将A的输出作为B的输入，但训练时只训练模型B，这时可以用detach()来切断

input_B = output_A.detach()

示例：

x = torch.tensor([2.], requires_grad=True)

a = torch.add(x, 1).detach()
b = torch.add(x, 2)
y = torch.mul(a, b)

y.backward()

print("requires_grad: ", x.requires_grad, a.requires_grad, b.requires_grad, y.requires_grad)
print("is_leaf: ", x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)
print("grad: ", x.grad, a.grad, b.grad, y.grad)

###result
requires_grad:  True False True True
is_leaf:  True True False False
grad:  tensor([3.]) None None None

四、逻辑回归

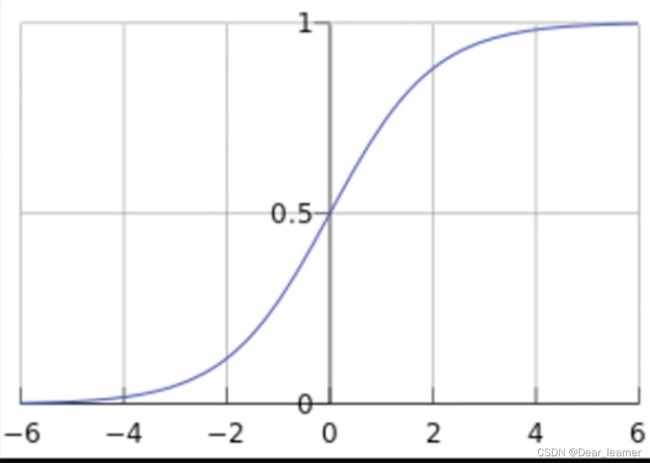
逻辑回归模型是线性的二分类模型，模型表达式为：

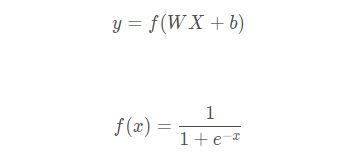
f(x)称为sigmoid函数，也称为Logistic函数


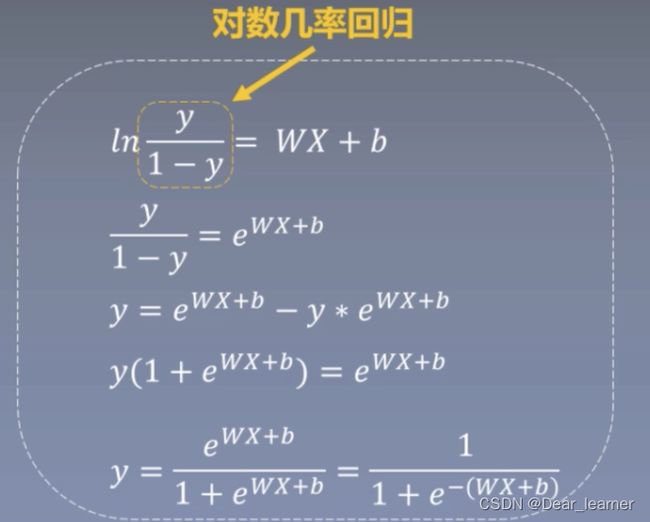
逻辑回归又称为对数几率回归

#数据生成
torch.manual_seed(1)

sample_nums = 100
mean_value = 1.7
bias = 1

n_data = torch.ones(sample_nums, 2)
x0 = torch.normal(mean_value*n_data, 1) + bias  # 类别0  数据shape=(100,2)
y0 = torch.zeros(sample_nums)   # 类别0， 数据shape=(100, 1)
x1 = torch.normal(-mean_value*n_data, 1) + bias   # 类别1， 数据shape=(100,2)
y1 = torch.ones(sample_nums)    # 类别1  shape=(100, 1)

train_x = torch.cat([x0, x1], 0)
train_y = torch.cat([y0, y1], 0)

#构建模型
class LR(torch.nn.Module):
    def __init__(self):
        super(LR, self).__init__()
        self.features = torch.nn.Linear(2, 1)  # Linear 是module的子类，是参数化module的一种，与其名称一样，表示着一种线性变换。输入2个节点，输出1个节点
        self.sigmoid = torch.nn.Sigmoid()

    def forward(self, x):
        x = self.features(x)
        x = self.sigmoid(x)

        return x

lr_net = LR()     # 实例化逻辑回归模型

#选择损失函数
loss_fn = torch.nn.BCELoss()

#选择优化器
lr = 0.01
optimizer = torch.optim.SGD(lr_net.parameters(), lr=lr, momentum=0.9)

#模型训练
for iteration in range(1000):

    # 前向传播
    y_pred = lr_net(train_x)

    # 计算loss
    loss = loss_fn(y_pred.squeeze(), train_y)

    # 反向传播
    loss.backward()

    # 更新参数
    optimizer.step()

    # 清空梯度
    optimizer.zero_grad()

    # 绘图
    if iteration % 20 == 0:

        mask = y_pred.ge(0.5).float().squeeze()  # 以0.5为阈值进行分类
        correct = (mask == train_y).sum()  # 计算正确预测的样本个数
        acc = correct.item() / train_y.size(0)  # 计算分类准确率

        plt.scatter(x0.data.numpy()[:, 0], x0.data.numpy()[:, 1], c='r', label='class 0')
        plt.scatter(x1.data.numpy()[:, 0], x1.data.numpy()[:, 1], c='b', label='class 1')

        w0, w1 = lr_net.features.weight[0]
        w0, w1 = float(w0.item()), float(w1.item())
        plot_b = float(lr_net.features.bias[0].item())
        plot_x = np.arange(-6, 6, 0.1)
        plot_y = (-w0 * plot_x - plot_b) / w1

        plt.xlim(-5, 7)
        plt.ylim(-7, 7)
        plt.plot(plot_x, plot_y)

        plt.text(-5, 5, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
        plt.title("Iteration: {}\nw0:{:.2f} w1:{:.2f} b: {:.2f} accuracy:{:.2%}".format(iteration, w0, w1, plot_b, acc))
        plt.legend()

        plt.show()
        plt.pause(0.5)

        if acc > 0.99:
            break