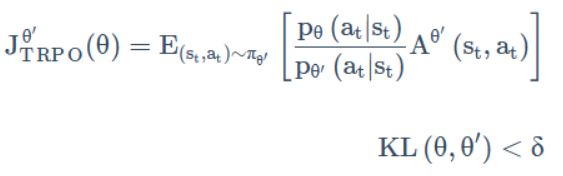RL 笔记（3）PPO(Proximal Policy Optimization)近端策略优化

RL 笔记（3） PPO

基本原理

PPO是在基本的Policy Gradient基础上提出的改进型算法

Policy Gradient方法存在核心问题在于数据的bias。因为Advantage估计是不完全准确的，存在bias，那么如果Policy一次更新太远，那么下一次采样将完全偏离，导致Policy更新到完全偏离的位置，从而形成恶性循环。因此，TRPO的核心思想就是让每一次的Policy更新在一个Trust Region里，保证policy的单调提升。

Policy gradient方法是on policy的，因此本来要求每次就使用on policy的数据进行训练。但是很显然，on policy的数据训练一次就扔掉太低效了。所以TRPO及PPO说是on policy，实际上大部分情况是off policy的，只能说是near on policy。怎么做呢？就是一次采样的数据分minibatch训练神经网络迭代多次，一般我们还会重复利用一下数据，也就是sample reuse。对于PPO，最佳的sample reuse=3，即一个样本使用3次。

那么，由于训练中使用了off policy的数据（只有第一个更新是on policy，后面都是off policy），数据分布不同了，因此，我们需要使用importance sampling来调整。

期望等价写成 $\int f(x)p(x)dx$ 然后引入新的采样分布q(x)进行变换$\int f(x)\frac{p(x)}{q(x)}q(x)dx$，这时候我们发现这和最大熵模型引入隐含变量的套路有点相似，然后就可以把原来x_{p的期望改写成x}q的期望。所以最终可以得到
$$\begin{gathered} E_{xp}[f(x)p(x)]=E_{x \\ q}[f(x)\frac{p(x)}{q(x)}] \end{gathered}$$
上述推导就是important sample的技巧。在这个式子中其中的$\frac{p(x)}{q(x)}$ 就是important weight。通过这个公式我们也可以想象得到，如果采样的分布p与真实的分布q差得很多，那么肯定会导致两个期望不一致。下图通过举了一个例子来讲解.

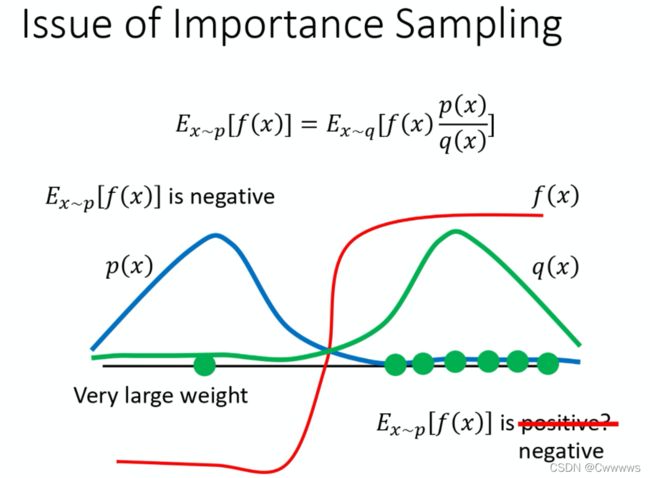
上图的p(x)与q(x)差异很大左边为负右边为正，当采样次数很少右边采样很多的情况，就会得出与右边为正的错误结果，但是如果在左边也被采样到一个样本时这个这个时候因为 $\frac{p(x)}{q(x)}$ 作为权重修正就相当于给左边的样本一个很大的权重，就可以将结果修正为负的。所以这就是 important weight的作用。但是我们也能看出来，采样次数要足够多，万一采样次数少只采到了一边那就凉凉了。

重要性采样的时候我们不能让分布差得太多。因此，我们可以给分布之间的距离——KL散度加一个约束 $\delta$，这就是TRPO

由于TRPO的loss是带条件的loss，用共轭梯度法进行计算，比较麻烦，因为它把 KL 散度约束当做一个额外的约束，没有放目标(objective)里面，所以它很难算。不能大规模应用，因此需要做简化，能够直接使用梯度下降实现，因此PPO应运而生。PPO则是将KL散度作为一个正则项放到损失函数里做优化。

PPO算法还有两个主要的变种：PPO-penalty和PPO-clip

首先来看PPO-penalty，也记为PPO-1

在这个算法里，我们会先初始化一个策略的参数 ${\theta }_0$ ，然后在每个迭代里，我们用 ${\theta }_k$和环境互动，生成一堆状态-动作对
然后我们根据互动的结果估测一下$A^{{\theta }_k}(s_t,a_t)$，接着使用 PPO 的优化的公式。但跟原来的策略梯度不一样，原来的策略梯度只能更新一次参数，更新完以后就要重新采样数据。但是，现在我们可以让 $\theta$更新很多次，因为由KL散度作为正则化项。

在 PPO 的论文里面还有一个 adaptive KL divergence。这边会遇到一个问题就是 $\beta$ 要设多少，它就跟正则化一样。正则化前面也要乘一个权重，所以这个 KL 散度前面也要乘一个权重，但 $\beta$ 要设多少呢？所以有个动态调整 $\beta$的方法。

我们先设一个 $\beta$的最大和最小值，作为容许界限。
如果优化一次之后，KL散度的项太大，则加大 $\beta$ 的值。反之，如果KL散度的项太小，则减少 $\beta$的值。

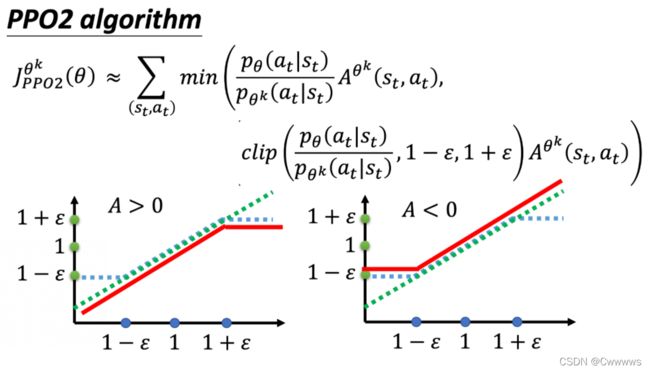
接着我们看PPO-clip，也记为PPO-2。

KL散度的计算可能很复杂，PPO-clip里面就没有KL散度。

这个$clip(x,1-ϵ,1+ϵ)$ 函数的作用，就是当 $x>1+ϵ$的时候输出$1+ϵ$ ，当 $x<1-ϵ$的时候输出 $1-ϵ$，其他的时候不变。

也就是你拿来做示范的模型跟你实际上学习的模型，在优化以后不要差距太大。

也就是当前policy和旧policy的偏差做clip，如果ratio偏差超过$ϵ$ 就做clip。这样，在实现上，无论更新多少步都没有关系，有clip给我们挡着，不担心训练偏了。

算法步骤

PPO收集一次样本训练几次？

根据上图，一次收集NT个样本，以某个minibatch size训练K个epoch。

从openai baseline的实现中可以看到，一般的设置是：

K=3，minibatch size = NT/4

K就是sample reuse的比率，表示一个样本用了多少次。

按照上面的设定，一次训练更新了12次。

这对于PPO非常重要，因为如果一次只更新1次，那么就是完全的on policy，ratio=1，ppo完全没用到clip，policy训练会非常慢。因此，最理想的是更新多次，更新到clip的边缘，最大化每一次采集样本的利用。

同时，基于上面的设定，actor/worker越多，一次采集的样本就越多，在控制训练次数的情况下，batchsize就会越来越大。对于PPO，batch 越大，对梯度的估计就越准，bias越小，所以效果会越好。在OpenAI Dota Five中，采用了极大的batchsize来加速训练。这也是large scale最大的意义。

OpenAI 训练OpenAI Dota Five时，每32个step 就将更新的参数发送给Forward Pass GPU，最快速度保证rollout使用最新的参数。然后Rollout Worker完全异步进行，疯狂采样。Learner不断拿buffer里面的数据进行训练，GPU，CPU都打满。

参考

1. 深度解读：Policy Gradient，PPO及PPG
2. 【强化学习】PPO(Proximal Policy Optimization)近端策略优化算法
3. 强化学习笔记：近端策略优化（PPO）
4. Proximal Policy Optimization Algorithms