机器学习实战(一)—— K-近邻算法(KNN)
本系列文章以《机器学习实战》为基础,并结合B站的UP主shuhuai008的机器学习白板推导系列合集,加强对机器学习基础算法的理解及运用。
如果大家对计算机视觉感兴趣可以参考博主的计算机视觉专栏:Python计算机视觉
近年来,深度学习大火,甚至有干倒其他的机器学习方法的趋势,但基础还是要打牢的,所以本篇文章用来介绍机器学习中比较基础的一个算法——K-近邻算法,希望能帮到大家。
本文章主要参考自《机器学习实战》,并加入自己的一些理解,尽量将该算法的基本原理和Python代码实现讲的通俗易懂。
目录
一 基本概念
1 概念
2 实现步骤
二 代码实现
三 约会网站分析
四 数据集以及《机器学习实战》获取
五 结束语
一 基本概念
1 概念
一般来说,我们确信‘如果你想了解一个人,那么先了解他周围的人’是一个真理,这也是K-近邻算法的主要思想。首先我们有一个训练数据集,它详细的记录了不同类别的样本的各种特征数据,比如我们想要通过身高和体重以及腰围等特征分别男生和女生,那么我们首先得得到大量的男生和女生的这些特征的数据;对这些数据进行处理过后,我们这时又得到一个同学的身高、体重以及其他特征的数据,那么我们该怎么判断该同学的性别呢?最简单的方法就是使用K-近邻算法了,首先计算这位同学的各项特征和训练集中的样本的欧氏距离(就是简单的两点之间的距离),选出和测试样本距离最近的k个样本,并计算出k个样本中不同类别的样本的占比,哪个种类的占比高就说明测试样本属于该样本。还是拿性别分类举例,如果我们得到6个最近的测试样本点,其中有5个样本是女生,只有一个样本是男生,那么我们就有很大的把握确定该测试样本是个女生。
除非我们的分类依据是头发长度、衣服等特征:
所以说除了k的大小,我们还要兼顾数据集的特征,尽量是独一无二的那种,哈哈哈哈。
2 实现步骤
step one: 收集数据(就是得到大量的训练样本)
step two: 对测试样本集进行结构化并分析
step three: 计算输入的测试样本和训练样本之间的距离
step four: 对测试样本进行分类
step five: 输出结果
二 代码实现
假设我们需要对医院的病人的病情等级进行分类,为了演示方便我们指定病人的病情分为A,B两个等级,分析指标也只有两项。
比如我们之前就得到的病人的各项数据指标以及病情等级如下表所示:
| 病人编号 | 病情等级 | 指标一 | 指标二 |
| 1 | A | 1.0 | 1.1 |
| 2 | A | 1.0 | 1.0 |
| 3 | A | 0.9 | 1.0 |
| 4 | A | 0.8 | 1.1 |
| 5 | A | 1.1 | 1.0 |
| 6 | B | 0.2 | 0.13 |
| 7 | B | 0.1 | 0.11 |
| 8 | B | 0.1 | 0 |
| 9 | B | 0 | 0 |
| 10 | B | 0 | 0.1 |
接下来我们要设计一个分类器来判断我们医院新接的病人的病情等级。
首先第一步我们要得到训练样本并将样本表示在图中:
"""
Author:XiaoMa
date:2021/12/1
"""
#导入需要的库
import numpy as np
import matplotlib.pyplot as plt
import operator
#得到训练样本集
def createDataSet():
group = np.array([[1.0, 1.1], [1.0, 1.0], [0.9, 1], [0.8, 1.1], [1.1, 1], [0.2, 0.13], [0.1, 0.11], [0.1, 0], [0, 0], [0, 0.1]])
labels = np.array(['A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'B'])
return group, labels #返回病人的病情指标和病情等级
group, labels = createDataSet()
plt.rcParams['font.family'] = 'SimHei' #将全局中文字体改为黑体
plt.rcParams['axes.unicode_minus'] = False #正常表示负号
A = group[0:5] #A组是样本集中的前五个
B = group[5:] #B组是样本集中的后五个
plt.scatter(A[:, 0], A[:, 1], color = 'aquamarine', label = 'A') #将数组中的前一列作为x轴,后一列作为y轴绘制在散点图中
plt.scatter(B[:, 0], B[:, 1], color = 'r', label = 'B')
plt.legend(loc = 'upper left') #添加图例
plt.show()接下来就是用代码实现K-近邻算法:
#K-近邻算法
def classify0(inX, dataSet, labels, k): #四个参数分别为:用于分类的输入向量inX,训练样本集dataSet,标签向量labels,最近邻居数目K
dataSetSize = dataSet.shape[0] #取得训练样本数目
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet #将输入的待分类样本进行x轴方向的四次复制并减去样本集,如计算(x1, y1)和(x2, y2)之间的距离,首先需要计算(x2-x1, y2-y1)
sqDiffMat = diffMat**2 #对得到的差值进行平方
sqDistances = sqDiffMat.sum(axis = 1) #求得(x2-x1)^2 + (y2-y1)^2
distance = sqDistances**0.5 #对平方和开根号得到两个数据之间的欧式距离
sortedDistIndicies = distance.argsort() #对距离进行argsort()默认的从小到大排列
classCount = {} #定义一个空的字典
for i in range(k): #开始选择距离最小的k个点
voteIlabel = labels[sortedDistIndicies[i]] #将原先的标签按照从小到大的顺序赋给voteIlabel
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
sortedClassCount = sorted(classCount.items(),
key = operator.itemgetter(1), reverse = True)#sorted()函数进行降序排列,最后返回发生频率最高的值
return sortedClassCount[0][0] #返回频率最高的样本点的标签使用上面的两个模块我们就可以对新来的病人的病情进行判定了,假设新来的病人的两项指标是(0.2,0.5):
"""
Author:XiaoMa
date:2021/12/1
"""
#导入需要的库
import numpy as np
import matplotlib.pyplot as plt
import operator
#得到训练样本集
def createDataSet():
group = np.array([[1.0, 1.1], [1.0, 1.0], [0.9, 1], [0.8, 1.1], [1.1, 1], [0.2, 0.13], [0.1, 0.11], [0.1, 0], [0, 0], [0, 0.1]])
labels = np.array(['A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'B'])
return group, labels #返回病人的病情指标和病情等级
group, labels = createDataSet()
plt.rcParams['font.family'] = 'SimHei' #将全局中文字体改为黑体
plt.rcParams['axes.unicode_minus'] = False #正常表示负号
A = group[0:5] #A组是样本集中的前五个
B = group[5:] #B组是样本集中的后五个
plt.scatter(A[:, 0], A[:, 1], color = 'aquamarine', label = 'A') #将数组中的前一列作为x轴,后一列作为y轴绘制在散点图中
plt.scatter(B[:, 0], B[:, 1], color = 'r', label = 'B')
plt.legend(loc = 'upper left') #添加图例
plt.show()
#K-近邻算法
def classify0(inX, dataSet, labels, k): #四个参数分别为:用于分类的输入向量inX,训练样本集dataSet,标签向量labels,最近邻居数目K
dataSetSize = dataSet.shape[0] #取得训练样本数目
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet #将输入的待分类样本进行x轴方向的四次复制并减去样本集,如计算(x1, y1)和(x2, y2)之间的距离,首先需要计算(x2-x1, y2-y1)
sqDiffMat = diffMat**2 #对得到的差值进行平方
sqDistances = sqDiffMat.sum(axis = 1) #求得(x2-x1)^2 + (y2-y1)^2
distance = sqDistances**0.5 #对平方和开根号得到两个数据之间的欧式距离
sortedDistIndicies = distance.argsort() #对距离进行argsort()默认的从小到大排列
classCount = {} #定义一个空的字典
for i in range(k): #开始选择距离最小的k个点
voteIlabel = labels[sortedDistIndicies[i]] #将原先的标签按照从小到大的顺序赋给voteIlabel
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
sortedClassCount = sorted(classCount.items(),
key = operator.itemgetter(1), reverse = True)#sorted()函数进行降序排列,最后返回发生频率最高的值
return sortedClassCount[0][0] #返回频率最高的样本点的标签
#对新来的病人进行判断
ind = [0.2, 0.5]#病人指标
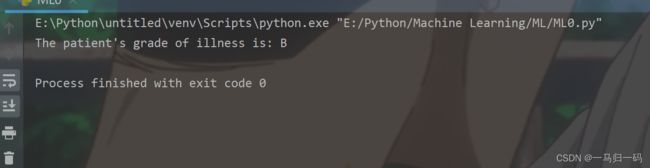
grade = classify0(ind, group, labels, 6)#分类器进行判断并返回频率最高的标签
print('The patient\'s grade of illness is:', grade) #得到结果可以得到的输出结果为:
我们也可以将该病人的指标绘制在散点图中进行判断:
plt.scatter(0.2, 0.5, color = 'b', label = '待分析病人')#将待分析病人的数据绘制到散点图中。此行代码添加到前面的得到训练样本集那里就行
可以看出待分析病人离B类较近,所以我们的分类器判断并没有出错。
三 约会网站分析
海伦一直在使用约会网站寻找中意的约会对象,但一直没有找到合适的约会对象,经过对自己以往的约会的分析,她把自己的以前的约会对象分为三类人:不喜欢的人、一般魅力的人、极具魅力的人,她还有一些自己收集的数据,来记录那些约会对象的各种指标。她把这些数据都保存在一个文件中,文件名为datingTsetSet.txt,她的观察样本的特征主要包括每年的飞行里程、每周的游戏时间占比以及每周消耗的冰淇淋公升数。
首先我们要做的是对读取的数据文件进行分析:
#分析数据文件
def file2matrix(filename): #创建分析函数
fr = open(filename)#打开数据集文件使用
array0Lines = fr.readlines()#读取文件的内容
number0fLines = len(array0Lines)#得到文件中数据的行数
returnMat = np.zeros((number0fLines, 3))#返回的NumPy矩阵,解析完成的数据:numberOfLines行,3列,两个括号,不然格式错误
classLabelVector = []
index = 0 #行数索引
for line in array0Lines:
line = line.strip()#截取所有回车字符
listFromLine = line.split('\t')#将整行数据分割成元素列表
returnMat[index, :] = listFromLine[0:3]#选取前三列元素存储到特征矩阵中
# 根据文本中标记的喜欢的程度进行分类,1代表不喜欢,2代表魅力一般,3代表极具魅力
if listFromLine[-1] == 'didntLike':
classLabelVector.append(1)
elif listFromLine[-1] == 'smallDoses':
classLabelVector.append(2)
elif listFromLine[-1] == 'largeDoses':
classLabelVector.append(3)
index += 1
return returnMat, classLabelVector#返回特征矩阵和标签对数据进行可视化,绘制到图中:
#将数据两两选择绘制到图中,并进行标签标记
datingDataMat, datingLabels = file2matrix('E:\Python\Machine Learning\ML\datingTestSet.txt')
#print(datingDataMat)#打印数据矩阵
numberOfLabels = len(datingLabels)
#对颜色和图例进行设置
LabelsColors = []
for i in datingLabels:
if i == 1:
LabelsColors.append('black')
if i == 2:
LabelsColors.append('orange')
if i == 3:
LabelsColors.append('red')
didntLike = plt.Line2D([], [], color = 'black', marker = '.',
markersize = 6, label = 'didntLike')#对图例进行设置
smallDoses = plt.Line2D([], [], color = 'orange', marker = '.',
markersize = 6, label = 'smallDoses')
largeDoses = plt.Line2D([], [], color = 'red', marker = '.',
markersize = 6, label = 'largeDoses')
a = plt.figure(figsize=(30, 10)) #创建画布
plt.subplot(131)
plt.scatter(datingDataMat[:, 1], datingDataMat[:, 2], c = LabelsColors)#第二例数据(玩游戏时间占比)和第三列数据(消耗的冰淇淋公升数)绘制散点图
plt.xlabel('玩游戏消耗的时间占比')#设置x轴
plt.ylabel('每周消耗的冰激凌升数')#设置y轴
plt.legend(handles = [didntLike, smallDoses, largeDoses])#添加图例
plt.subplot(132)
plt.scatter(datingDataMat[:, 0], datingDataMat[:, 1], c = LabelsColors)#第一列数据(每年的飞行里程)和第二列数据(玩游戏时间占比)绘制散点图
plt.xlabel('每年的飞行里程')
plt.ylabel('玩游戏消耗的时间占比')
plt.legend(handles = [didntLike, smallDoses, largeDoses])
plt.subplot(133)
plt.scatter(datingDataMat[:, 0], datingDataMat[:, 2], c = LabelsColors)#第一列数据(每年的飞行里程)和第三列数据(消耗的冰淇淋公升数)绘制散点图
plt.xlabel('每年的飞行里程')
plt.ylabel('每周的冰激凌升数')
plt.legend(handles = [didntLike, smallDoses, largeDoses])
plt.savefig('E:\From Zhihu\data.png', dpi = 960)#保存图像
plt.show()对数据进行归一化:
我们知道K-近邻算法是计算的欧几里得距离,如果要计算下表中中的3和4之间的距离,那么每年的飞行里程数就占了很大的权值,导致其他两项的决定权不大,所以我们要对其进行归一化:
一般来说,原始数据和最小数据的差值比上最大数据和最小数据的差值就是对数据进行归一化:
![]()
def autoNorm(dataSet):
minVals = dataSet.min(0) #获得数据的最小值
maxVals = dataSet.max(0) #获得数据的最大值
ranges = maxVals - minVals #最大值和最小值的差值
normDataSet = np.zeros(np.shape(dataSet)) #shape(dataSet)返回dataSet的矩阵行数列数
m = dataSet.shape[0] #返回dataSet的行数
normDataSet = dataSet - np.tile(minVals, (m, 1)) #原始值减去最小值
normDataSet = normDataSet / np.tile(ranges, (m, 1)) #除以最大和最小值的差,得到归一化矩阵
return normDataSet, ranges, minVals #返回归一化后的特征矩阵、数据范围、最小值进行打印可得:
datingDataMat, datingLabels = file2matrix('E:\Python\Machine Learning\ML\datingTestSet.txt')
nor, ran, min = autoNorm(datingDataMat)
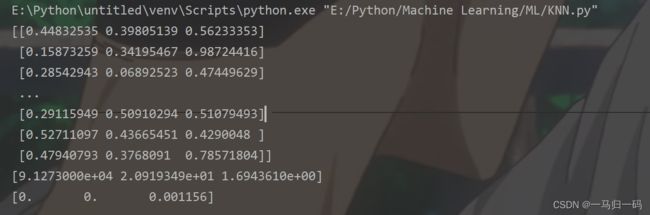
print(nor)
print(ran)
print(min)使用该分类器海伦可以直接输入约会对象的特征并判定这个人的魅力(如果不喜欢输出为:you don't like this person,如果这个人魅力一般,输出为:you will like this person,如果这个人魅力爆表,输出为:you will be addicted to this person.)
def classifyPerson(): #定义分类器
#输出结果
resultList = ['don\'t like this person', 'will like this person', 'will be addicted to this person']
#三种特征用户输入
precentTats = float(input("玩视频游戏所耗时间百分比:"))
ffMiles = float(input("每年获得的飞行常客里程数:"))
iceCream = float(input("每周消费的冰激淋公升数:"))
#打开的文件名
filename = "datingTestSet.txt"
#打开并处理数据
datingDataMat, datingLabels = file2matrix(filename)
#训练集归一化
normMat, ranges, minVals = autoNorm(datingDataMat)
#生成NumPy数组,测试集
inArr = np.array([precentTats, ffMiles, iceCream])
#测试集归一化
norminArr = (inArr - minVals) / ranges
#返回分类结果
classifierResult = classify0(norminArr, normMat, datingLabels, 3)
#打印结果
print("You %s" % (resultList[classifierResult - 1]))
classifyPerson()#运行分类器尝试运行并输出结果:
可以看出这个人属于魅力一般的人,其实也可以从前面的图中分类出来,在三幅图中原点附近的点都是一般魅力的橙色的点。
四 数据集以及《机器学习实战》获取
有很多博主已经提供了大量的资料,大家可以去进行获取,也可以在我的网盘中获取:
链接:https://pan.baidu.com/s/1zrsXMEQjB18dgaAtXw-KOQ
提取码:jmh3
五 结束语
本篇文章主要介绍了K-近邻算法以及实现方式,并简单实现了约会网站的分析,书中还有手写字体的识别,如果感兴趣1也可以去尝试,有时间再更。