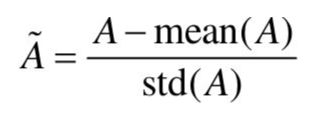【Pytorch学习笔记九】 深度学习中数据的归一化(Normalization)
文章目录
-
- 1 为什么要归一化?
- 2.归一化对比
- 3 pytorch中的归一化
1 为什么要归一化?
在某些线性规划问题中,特征的数值范围和标签的数值范围差别很大,或者不同特征之间的数值范围差别很大。这时,某些权重值可能会特别大,这为优化器学习这些权重值带来了困难。在这种情况下常常对数据进行归一化(normalization),使得优化器面对的每个特征的数值或标签的数值在一个相对固定的范围内。torch.mean()函数和torch.std()函数可以用于求解张量的均值和方差。利用这两个函数,我们可以将某个特征或标签 归一化为
归一化得到的特征或标签的均值为0,方差为1。这样,它们的取值范围就相对固定了。
批标准化的优点有如下:
- 可以使用更大的学习率,加速模型收敛
- 可以不用精心设计权值初始化
- 可以不用 dropout 或者较小的 dropout
- 可以不用 L2 或者较小的 weight decay
- 可以不用 LRN (local response normalization)
2.归一化对比
import torch.nn
import torch.optim
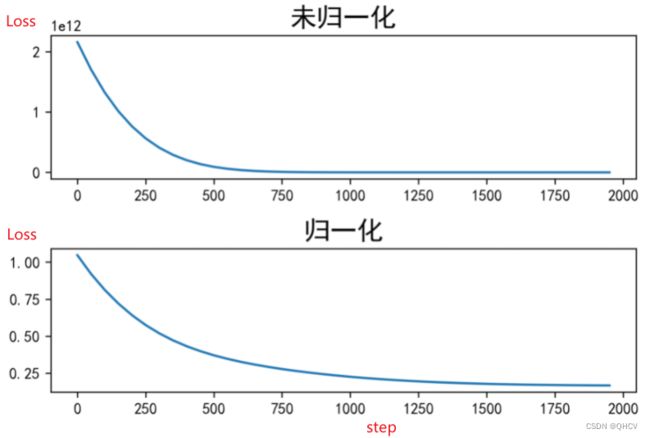
print('{:*^30}'.format("未归一化"))
x = torch.tensor([[1000000, 0.0001], [2000000, 0.0003],
[3000000, 0.0005], [4000000, 0.0002], [5000000, 0.0004]])
y = torch.tensor([-1000., 1200., 1400., 1600., 1800.]).reshape(-1, 1)
#线性层
fc = torch.nn.Linear(2, 1)
criterion = torch.nn.MSELoss()
optimizer = torch.optim.Adam(fc.parameters())
step_list = []
loss_list = []
for step in range(10001):
if step: #第一次循环不运行
optimizer.zero_grad()
loss.backward()
optimizer.step()
pred = fc(x)
loss = criterion(pred, y)
if step % 50 == 0:
print('step = {}, loss = {:g}'.format(step, loss))
step_list.append(step)
loss_list.append(loss)
print('{:*^30}'.format("归一化"))
x = torch.tensor([[1000000, 0.0001], [2000000, 0.0003],
[3000000, 0.0005], [4000000, 0.0002], [5000000, 0.0004]])
y = torch.tensor([-1000., 1200., 1400., 1600., 1800.]).reshape(-1, 1)
x_mean, x_std = torch.mean(x, dim=0), torch.std(x, dim=0)
#归一化
x_norm = (x - x_mean) / x_std
y_mean, y_std = torch.mean(y, dim=0), torch.std(y, dim=0)
y_norm = (y - y_mean) / y_std
step_list_n = []
loss_list_n = []
fc = torch.nn.Linear(2, 1)
criterion = torch.nn.MSELoss()
optimizer = torch.optim.Adam(fc.parameters())
for step in range(10001):
if step:
optimizer.zero_grad()
loss.backward()
optimizer.step()
pred = fc(x_norm)
loss = criterion(pred, y_norm)
if step % 50 == 0:
print('step = {}, loss = {:g}'.format(step, loss))
step_list_n.append(step)
loss_list_n.append(loss)
import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl
mpl.rcParams["font.sans-serif"]=["simHei"] #配置字体文件
mpl.rcParams["axes.unicode_minus"] = False #设置正常显示符号
plt.figure(dpi=300)
# 建立 subplot 网格,高为 2,宽为 1
# 激活第一个 subplot, 位于第一行
plt.subplot(2, 1, 1)
# 绘制第一个图像
plt.plot(step_list[:40],loss_list[:40])
plt.title('未正则化',fontsize='xx-large',fontweight='heavy')
# 将第二个 subplot 激活,并绘制第二个图像, 位于第2行;
plt.subplot(2, 1, 2)
plt.plot(step_list_n[:40],loss_list_n[:40])
plt.title('正则化',fontsize='xx-large',fontweight='heavy')
plt.tight_layout()
# 展示图像
plt.savefig("对比.jpg")
plt.show()
无归一化的损失曲线下降到一定数值就不再快速下降。在快速下降部分,是对其中的一个特征进行了充分优化。当那个特征带来的红利用尽时,再次迭代就不能再大幅度减少损失。在后续的迭代中,损失仍然能够缓慢下降,但是由于下降的速度太慢,所以在图中看起来就像没有变化一样。理论上,只要迭代次数足够多,损失仍然能够下降到最小值。只是这个过程将非常漫长,以至于没有实际的意义。
3 pytorch中的归一化
在 PyTorch 中,有 3 个 Batch Normalization 类
- nn.BatchNorm1d(),输入数据的形状是 B × C × 1 D f e a t u r e B \times C \times 1D_{feature} B×C×1Dfeature
- nn.BatchNorm2d(),输入数据的形状是 B × C × 2 D f e a t u r e B \times C \times 2D_{feature} B×C×2Dfeature:
- nn.BatchNorm3d(),输入数据的形状是 B × C × 3 D f e a t u r e B \times C \times 3D_{feature} B×C×3Dfeature
其中B代表批大小,C代表特征数,D代表特征维度,如:数据的形状是:(3, 5, 1),表示一个 mini-batch 有 3 个样本,每个样本有 5 个特征,每个特征的维度是 1。
#以BatchNorm1d为例
torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
#num_features:一个样本的特征数量,这个参数最重要
#eps:在进行标准化操作时的分布修正项
#momentum:指数加权平均估计当前的均值和方差
#affine:是否需要 affine transform,默认为 True
#track_running_stats:True 为训练状态,此时均值和方差会根据每个 mini-batch 改变。False 为测试状态,此时均值和方差会固定
类似的pytorch中还有Layer Normalization、instance Normalization及Group Normalization。
参考资料:
神经网络与PyTorch实战(肖智清 著)
https://pytorch.zhangxiann.com/6-zheng-ze-hua/6.2-normalization#layer-normalization
欢迎关注公众号【智能建造小硕】(分享计算机编程、人工智能、智能建造、日常学习和科研经验等,欢迎大家关注交流。)