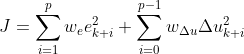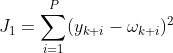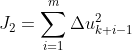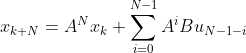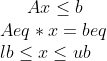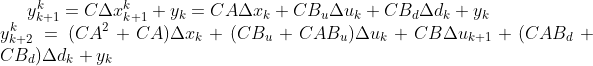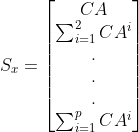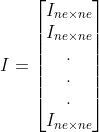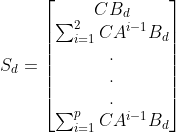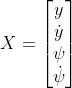MPC算法学习(1)

 

目录

一、了解MPC

1.MPC → Model PredictIve Control

2.MPC基本工作原理

二、MPC设计

1.MPC参数设计

2.MPC使用范围

 3.MPC速度优化

三、MPC推导

1.基于单位脉冲响应的公式推导

2.基于状态空间的推导

四、仿真实例

1.SISO系统

2.MIMO系统

3.基于simulink的仿真

 4.车辆横向运动状态空间模型的推导

5.自适应MPC

五、多种MPC类型拓展

1.非线性MPC（nonlinear MPC\NMPC）

2.线性时变MPC（LTV MPC）

---

一、了解MPC

1.MPC → Model PredictIve Control

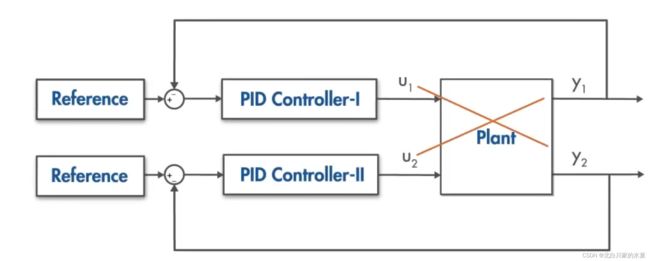
（1）处理对象：输入输出之间有交互作用的多输入多输出系统（MIMO System）

（2）PID 对于该类型系统的局限性：

① 如上图所示，两个回路之间没有交叉，就像二者是相互独立一样

② 如果系统（Plant）足够大，因为调参十分困难

MPC的优势：

① 可以处理多变量问题

② 可以添加约束

e.g.在驾驶时，汽车有期望的轨迹，同时有加速约束

③ 有预览功能（类似前馈），以改善控制器性能

（3）MPC硬件条件

需要功能强大的，内存大的处理器，因为每个时间步骤都需要在线优化问题

2.MPC基本工作原理

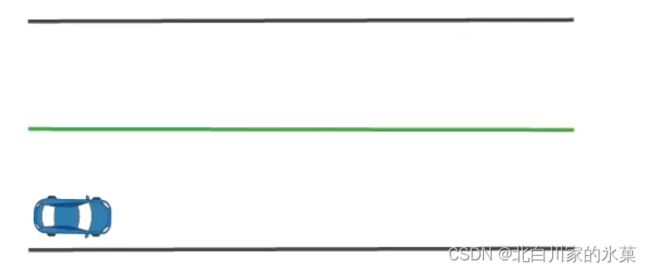
以如图的过程为例，期望汽车沿中线运动：

MPC在该过程中的作用如下：
（1）首先，预测一条p步之后可以到达中线的路径（这里有个问题，这个p如何选择呢？选择过少会不会导致无解？过多会不会降低效率？）该过程涉及了汽车模型本身的使用。

显然这种路径有无穷多条，我们选择“代价（cost）"最小的一条，该过程由优化器（optimizer）完成。对于这种情况，对应的cost包括：

① 汽车在此p步中，每一步的位置都会与中线有一个相对应的偏差值，我们想要这个偏差值之和最小

② 汽车每一次的打舵量要尽可能的小，否则会让乘客十分不舒服，即打舵量之和应该也最小

综上，应该让二者加权和最小，即：

 我们总会找到一条使J最小的路径

一般地，有：

（2）进行条件约束，例如车必须在车道里，同时方向盘的转角应该有一个范围

（3）进行该路径中p步中的第一步，即进行响应角度的方向盘转动，而将后面的步骤舍弃

（4）在新的起点重复以上过程，下一次预测的结果可能与上次的预测不同，因为可能有干扰的存在（风，湿滑的路面）

根据上述过程，我们可知，我们每次运动后都在预测未来p步的路径，因此我们所谓的”预测视界“是向前运动的，因此MPC也被称为后退视界控制。

二、MPC设计

1.MPC参数设计

 （1）基本参数

① 采样时间 → 决定控制器执行控制算法的速率

太大：无法快速处理扰动

太小：计算负荷过大

因此一般情况下选择：

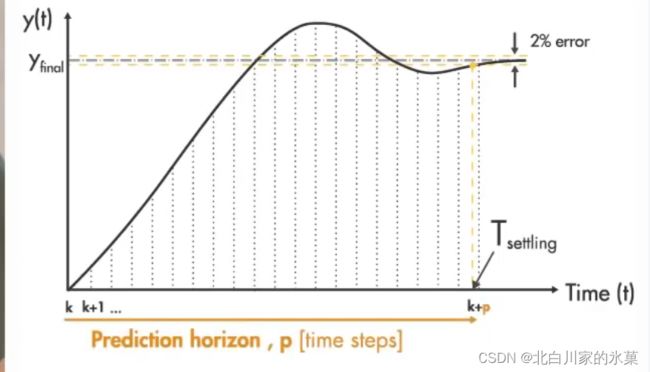
② 预测范围：即预测未来事件步长的数量

太短：假如刹车需要5s，但是我只能预测到两秒外的视界，距离交通灯2s路程时开始制动，此时已经来不及了，我们必定会冲过头

太长：可以涵盖之后很长一段时间内的范围，但是如果发生突发情况，比如行人过马路，此时我们必须停车，那么之后就要重新预测，假如我们预测了未来20s的事件，在5s时发生了行人过马路事件，那么后面15s的内容我们就白预测了，即浪费了算力。当然，任何长度的预测范围都可能发生突发情况，但是预测范围越长，我们进行无效预测的时间越长，出现无效预测的概率越大。

因此，我们必须选择一个涵盖整个系统动态的预测范围，但是也不宜太长

建议选择步长20-30

③ 控制范围：控制移动到时间步长m的次数

步长m较大时，可以获得更好的预测，但是会增加复杂性，我们甚至可以是控制范围与预测范围相同，但是一般只有前几个控制动作才对输出行为有影响，因此控制范围最好是预测范围的10%到20%，至少2-3步

进一步理解：

假如”我“是一个学生，“我”的能力对于导师而言是完全可知的，在工程上，就是”我“的模型是完全可知的，导师会给我安排学习任务，假如导师在知道我能力的情况下做好了未来七天的计划（预测范围），但是只给我安排了五天的学习任务（控制范围），但在我完成一天学习后，我可能超额完成任务，也可能不达标（外界干扰导致没有达到预测结果），因此我只完成被安排的学习任务的第一天的任务，在此之后，导师再次制定七天之后的计划，并给我安排下五天的计划。长此以往，导师发现，制定七天的任务太多了，会浪费他宝贵的时间，因此之后改为制定五天计划，安排三天计划。

④ 硬约束和软约束：硬约束必须服从，软约束不一定服从，如果全是硬约束，比如输入输出全部采用硬约束，那么可能会导致无法解决优化问题

软约束可以通过优化问题保证违反程度较小

⑤ 权重：

通过权衡来衡量竞争目标之间的权重（如输入和输出有不同权重）

同时，对于同一个组，我们可以对不同的成员分配权重（如第一输出和第二输出有不同权重）

2.MPC使用范围

（1）线性系统，线性约束条件，有二次cost函数→ 可以使用线性MPC

（2）非线性系统，同样可以使用线性MPC，原理是线性化

         如：在自适应MPC中，随着运行条件变化，工作点也变化，因此可以动态地在工作点附近进行线性化，从而动态获得线性模型

注：对于自适应MPC，在不同运行条件下，状态数和约束数不会改变

如果随着操作条件变化，状态数改变：使用增益预定MPC，在感兴趣的工作点进行离线显性化，针对每个工作点设计线性

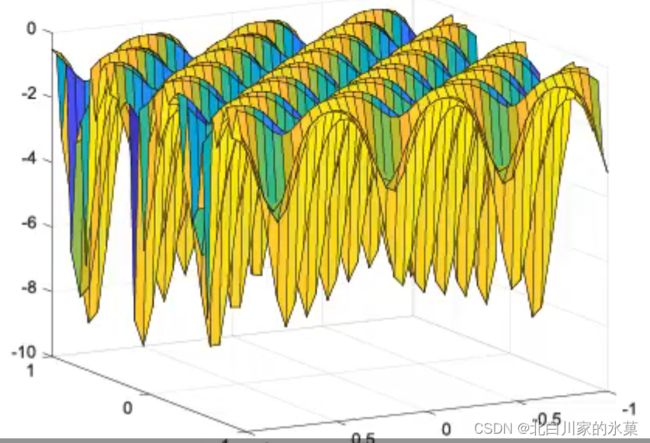
（3）如果非线性系统难以进行线性化，可以使用非线性MPC，此时做出的预测更加准确，但同时，优化问题变得不凸，即可能有很多局部最优解，如图：

 3.MPC速度优化

I.（1）模型简化，可以减少状态数量

（2）预测范围适当减小

（3）控制范围适当减小

（4）减少约束数量

（5）降低数据表示精度

II.当采样时间特别小时，可以采用显式MPC（Implicit MPC）

显式MPC特点：离线解决问题，而不是在线优化，对于范围内每个x值，都预先计算最佳解，

III. 采用次优解决方案

 如果想在采样时间内找到解决方案，同时还有多余时间执行其他任务，可以确定迭代次数最大值，当达到最大次数时，停止最优化

三、MPC推导

1.基于单位脉冲响应的公式推导

步骤：

（1）确定模型

（2）进行预测

（3）滚动优化

（4）误差补偿

对于模型已知的系统，其单位脉冲响应在每个采样时刻都是可知的，根据离散卷积定理，此时输出可以用输入和单位脉冲响应的卷积计算

 假设在k+1时刻开始输入信号，对等式两侧进行差分，则在k+1时刻及其后，有：

     

.

.

这里需要注意一点，由于控制范围是m，预测范围为p，一般情况下，控制范围比预测范围要小一点，因此m会小于p，而控制范围反应的是输入信号，因此u只有m个序号，即从k到k+m-1，在第m步预测之后，后面的累加项一直都是m个，因为在第m个采样时间后，由于此时已经超出控制范围，在此之后，输入量保持上一时刻不变，因此取差分后为0

整理为矩阵形式，如下：

接下来进行滚动优化，优化原则是代价函数的值最小，代价函数分为以下几个部分：

首先，我们希望真实输出与期望轨迹之间的偏差平方和最小，即：

其中是预测的轨迹，可以通过真实输出与参考输出表示，即：

这相当于是一个滤波，在[0,1]之间，在i足够大时，趋近于参考值

另外地，我们希望每次输入的偏差之和小一点，以让用户有更好的体验，则有：

则整体的代价函数为：

其中Q、R分别为两项代价的权重

     

 每个元素可以不一样，这样可以分配各个状态变量内部的权重

写成矩阵形式为：

一般地，Q和R都是对角矩阵

对求偏导数，有：

得：

 最后进行误差补偿：

假如在k时刻，我们获得了之后p个时刻的预测值：

 在k+1时刻，我们获得了的真实值

则我们可以评估预测的误差：

设补偿系数为h，h一般为0.5，这里注意下面的公式没有打错，一直都是用k+1点的误差补偿，所以才需要一个补偿系数，因为其他点的误差不见得等于k+1点的误差

则补偿后，有：

.

.

.

 用矩阵表示，为：

本质上这是一个状态反馈

则根据滚动预测原则：

其中S为移位矩阵（p*p）

可能看到这里有点乱，我其实一开始也乱了，但是这里捋顺一下思路就好了，乱的原因主要是变量太多，难以区分。

总结：整体的思路是这样的：

我们首先对于这个模型的单位脉冲响应已经得知，那么我们可以获得矩阵A，根据卷积定理，我们可以获得输入变化量，输出变化量，输出初态的关系，即：

其实根据我个人理解，这个也可以认为是：响应=零输入响应+零状态响应

这个式子只是一个理论基础，用处是告诉我们：只要你知道一个输入变化量，我们就可以预测这个系统的输出

那么这个输入变化量他可不是乱取的，他是有备而来，这就是所谓的优化问题，根据上述推导的公式我们可以得知，取何值时可以得到最优解

由于模型有误差，再加上可能存在扰动之类的问题，因此我们需要加一个反馈校正，在这里选择的是状态反馈，我们的目的是在目前的时间点，进行预测之后，对这个预测进行合理的矫正，给他加个buff，那么这个buff是怎么算出来的呢，我们不是知道当前时间点的真实值吗，并且我们肯定有之前预测的此刻的预测值数据，我们做一个差，此时我们就知道偏差是多少，乘以一个合适的H矩阵，加上原来的预测值，可以让预测更合理。

当然，我们说这是一个滚动预测过程，那么滚动体现在何处呢？我们预测完这个时刻后，一定要来到下一个时刻，那么到达“下一个”时刻(k+2)时，k+1就成了过去时，k+1的预测值又可以用来和k+2真实值作差，评估误差，以此类推，以完成滚动，这时S矩阵便派上用场。

2.基于状态空间的推导

基本的原理和冲激响应模型是一样滴，只不过使用的模型不一样

我们不妨设E=Y-R=X，即用状态变量表示

设在k时刻，初始误差为，其中是一个向量，因为他可能有很多输出

则根据现代控制理论的知识：

若我们设

则有：

.

.

.

将上面一坨公式整理为矩阵形式：

其中，

为到向量组合，值得注意的是，到在这里是预测值，即在k点对未来做的预测，我懒得加帽子了。N为预测范围

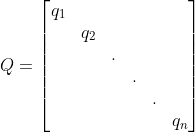
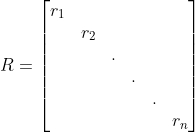
记

对于MIMO系统，由于有多个输入，则u为p维向量，所以B为n×p矩阵，且C矩阵上面应该有n行0，

M：（N+1）n×n C：（N+1）n×Np :(N+1)n×1 :Np×1

对于代价函数：

其中最后一项是final cost，由于其比过程误差更重要，所以要单独拿出来

整理代价函数：

其中：

        

代入：

得：

由于J是一个标量，因此内部任何一个式子都是标量，同时：

 互相成转置关系，可以合并

 令：

则：

最后是约束的添加

对于matlab中的quadprog函数，调用方法如下:

[x,fval,exitflag]=quadprog(H,f,A,b,Aeq,beq,lb,ub,x0​,options)

应用时，首先对于的限制可以用lb和ub表示

对于状态变量，若有：

代入模型：

深入理解：
对代价函数求导后，可以得到一个和的关系，本质上就是得到一个输入和状态空间的关系，则输入和状态有：的关系，本质上，这是一个状态反馈。对于完全能控的系统，状态反馈可以任意配置极点，当然可以保证极点在单位圆内，则系统可以镇定。

这里可以进一步定量推导：

设：

其中为可测外部干扰变量

两边取微分：

输出：

进一步地：

.

.

.

这个推法和前面差不多，不多说了

则有：

其中：

设参考输入为

定义：

代入

令

则：

极值为：

这里计算时注意，由于J是个标量，因此其中相加的几个量都是标量，则：

我们只需要第一个元素，即：

不妨设：

即：

是对于未来参考输入的前馈补偿

是对于可预测扰动的前馈补偿

是状态反馈

四、仿真实例

1.SISO系统

设系统状态空间方程为：

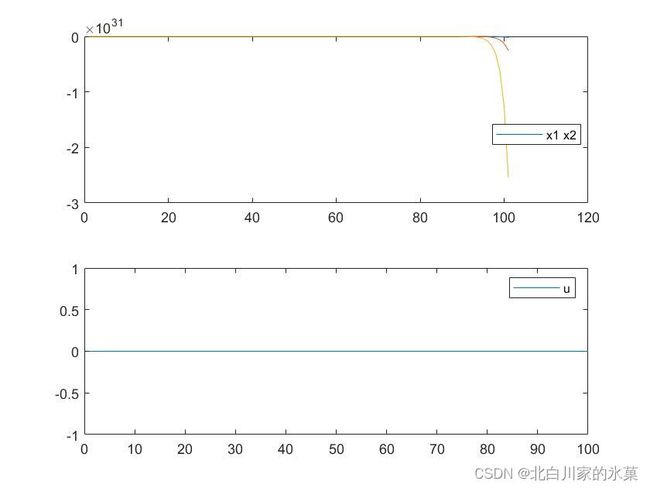
对于该系统，零输入响应如图：

 其实从系统A矩阵可以看出，该系统特征值在单位圆外面，所以肯定是发散的

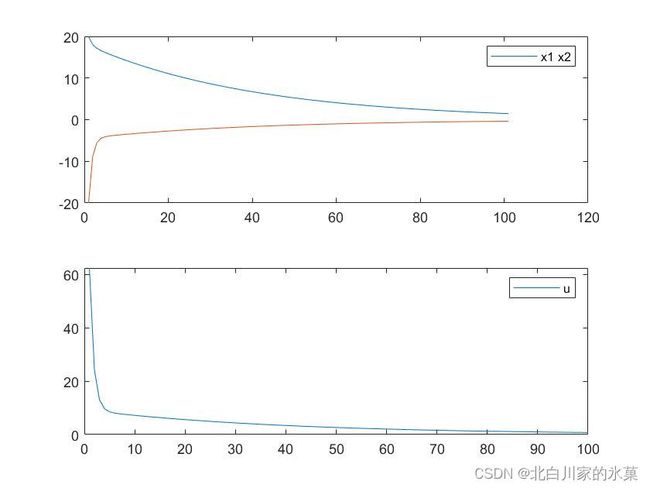
对于单输入系统，加入MPC后，结果如下：

可见加入MPC控制后，系统收敛了，MPC的确起到了状态反馈的作用，使得新的闭环系统的极点处于单位圆内。

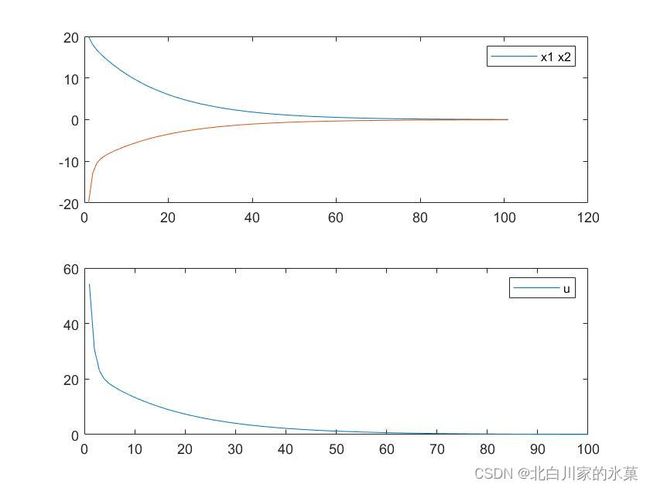
如果提高的权重，效果如下：

如果提高输入的权重，结果如下：

 显然状态空间衰减变慢

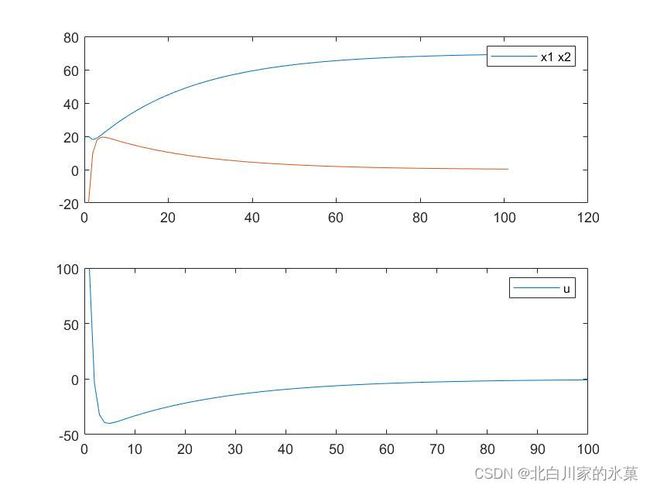
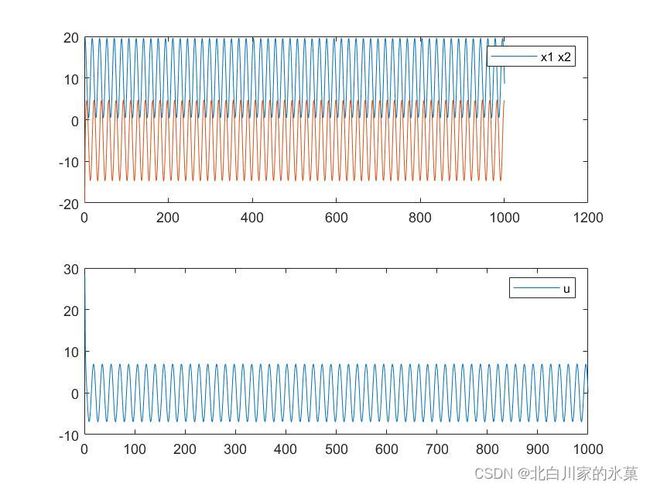
如果期望值不是0，如期望终值为70，结果如下：

改变目标值的本质原理如下：

一般情况下，对于状态空间 ，如果A的特征值在单位圆内（离散状态空间），那么该系统必能收敛至0

设期望值为，那么偏差值：

两边取微分：

因此偏差也可以衰减至0，且和原状态空间的A矩阵相同，因此可以套用原状态空间的控制方法

下图来自现代控制理论

 综上，SISO系统MPC控制代码如下：

mpc_sim.m

clear;
clc;
A=[1 0.1;0 2];
B=[0;0.5];
%x=Ax0+Bu
Q=[2 0;0 1];%weight of error cost function
F=[1 0;0 1];%weight of error cost function(last step)
R=[0.1]; %weight of input cost function



n=size(A,1);%the dimension of the state space
p=size(B,2);%the dimension of input vector

k_step=100;%steps of my state space 

X_k=zeros(n,k_step);%set state space vector
X_d=zeros(n,k_step);



X_k(:,1)=[20;-20];%initialization of the state space 

U_k=zeros(p,k_step);%set input vector 

N=5; %prediction horizon

basic = eye(n);
[E,H]=Cal_matrix(A,B,Q,R,F,N);
X_expect=[70;0];








for k = 1:k_step
    X_d(:,k)=X_k(:,k)-X_expect;
    U_k(:,k)=Prediction(X_d(:,k),E,H,N,p);%with k adding,the initial value of
    %X_k also changes,so this is what is called recursive optimization 
    
    X_d(:,k+1)=A*X_d(:,k)+B*U_k(:,k);%recursion of state space
    X_k(:,k+1)=X_d(:,k+1)+X_expect;
end 


subplot(2,1,1);

for i= 1 :size(X_k,1)
    plot(X_k(i,:));
    hold on
end 
legend("x1 x2");
hold on;


subplot(2,1,2);



for i =1:size(U_k,1)
    plot (U_k(i,:));
end

legend("u");

Cal_matrix.m

function [E,H]=Cal_matrix(A,B,Q,R,F,N)

n=size(A,1);
p=size(B,2);


M=[eye(n);zeros(N*n,n)];
C=zeros((N+1)*n,N*p);



temp=eye(n);


for i =  1:N
    rows=i*n+(1:n); %this mean from which lines should we start at this step,
    %for each matrix has not a single row,we use 'i*n',it starts from n+1
    C(rows,:)=[temp*B,C(rows-n,1:end-p)]%"rows-n,1:end-p"means using the 
    %elements of last step,end -p equals to let out a place for 'temp*B'
    temp=A*temp;
    M(rows,:)=temp;
end

Q_bar=kron(eye(N),Q);%in order to make a diagonal matrix with Q
% as its diagonal elements

Q_bar=blkdiag(Q_bar,F);
R_bar=kron(eye(N),R);


G=M'*Q_bar*M;
E=C'*Q_bar*M;
H=C'*Q_bar*C+R_bar;
end

prediction.m

function u_k=Prediction(x_k,E,H,N,p)
U_k=zeros(N*p,1);
U_k=quadprog(H,E*x_k);
u_k=U_k(1:p,1);%only use the first step
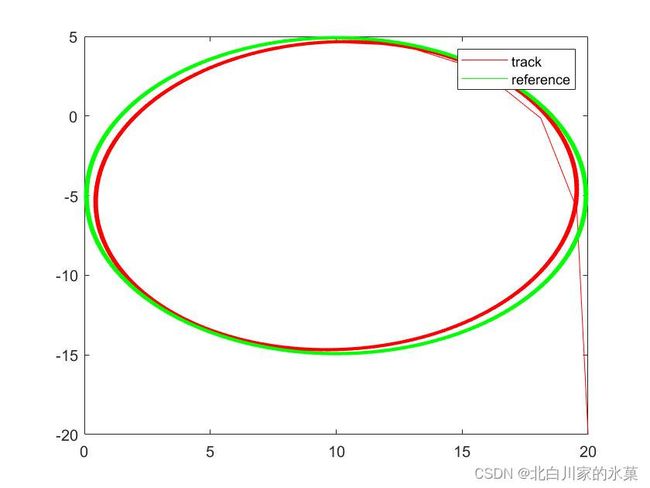
end

另外，令该系统跟踪圆形轨迹，结果如下:

 

主函数对应如下：

clear;
clc;
A=[0.3 0;0 1];
B=[0;0.5];
%x=Ax0+Bu
Q=[1 0;0 1];%weight of error cost function
F=[1 0;0 1];%weight of error cost function(last step)
R=[0.1]; %weight of input cost function



n=size(A,1);%the dimension of the state space
p=size(B,2);%the dimension of input vector

k_step=1000;%steps of my state space 


X_k=zeros(n,k_step);%set state space vector
X_d=zeros(n,k_step);




X_k(:,1)=[20;-20];%initialization of the state space 

U_k=zeros(p,k_step);%set input vector 

N=5; %prediction horizon

basic = eye(n);
[E,H]=Cal_matrix(A,B,Q,R,F,N);
X_expect=zeros(n,k_step);








for k = 1:k_step
    X_expect=[10*cos(360/k_step*k)+10;10*sin(360/k_step*k)-5];
    X_d(:,k)=X_k(:,k)-X_expect;
    U_k(:,k)=Prediction(X_d(:,k),E,H,N,p);%with k adding,the initial value of
    %X_k also changes,so this is what is called recursive optimization 
    
    X_d(:,k+1)=A*X_d(:,k)+B*U_k(:,k);%recursion of state space
    X_k(:,k+1)=X_d(:,k+1)+X_expect;
end 

figure(1)
subplot(2,1,1);

for i= 1 :size(X_k,1)
    plot(X_k(i,:));
    hold on
end 
legend("x1 x2");
hold on;


subplot(2,1,2);



for i =1:size(U_k,1)
    plot (U_k(i,:));
end

legend("u");
hold on;
figure(2);

plot(X_k(1,:),X_k(2,:),'r')

hold on;

X_exp_vec=zeros(n,k_step);
for k = 1:k_step
    X_exp_vec(:,k)=[10*cos(360/k_step*k)+10;10*sin(360/k_step*k)-5];
end
plot(X_exp_vec(1,:),X_exp_vec(2,:),'g')
legend("track","reference");

2.MIMO系统

对于MIMO系统：

仿真代码如下：

clear;
clc;
A=[1 0.1;-1 2];
B=[0.2 1;0.5 2];
%x=Ax0+Bu
Q=[1500 0;0 1500];%weight of error cost function
F=[1 0;0 1];%weight of error cost function(last step)
R=[0.1 0;0 0.1]; %weight of input cost function
lb=[-200;-200];
ub=[200;200];
MIN=[-20;-20;-20;-20;-20;-20;-20;-20;-20;-20;-20;-20];
MAX=[20;20;20;20;20;20;20;20;20;20;20;20];






n=size(A,1);%the dimension of the state space
p=size(B,2);%the dimension of input vector

k_step=1000;%steps of my state space 


X_k=zeros(n,k_step);%set state space vector
X_d=zeros(n,k_step);




X_k(:,1)=[20;-20];%initialization of the state space 

U_k=zeros(p,k_step);%set input vector 

N=5; %prediction horizon

basic = eye(n);
[E,H,M,C]=Cal_matrix(A,B,Q,R,F,N);

A_k=[C;-C];
b_k=[MAX-M*X_k(:,1);-MIN+M*X_k(:,1)];



X_expect=zeros(n,k_step);








for k = 1:k_step
    X_expect=[10*cos(360/k_step*k)+10;10*sin(360/k_step*k)-5];
    X_d(:,k)=X_k(:,k)-X_expect;
    U_k(:,k)=Prediction(X_d(:,k),E,H,N,p,A_k,b_k,lb,ub);%with k adding,the initial value of
    %X_k also changes,so this is what is called recursive optimization 
    
    X_d(:,k+1)=A*X_d(:,k)+B*U_k(:,k);%recursion of state space
    X_k(:,k+1)=X_d(:,k+1)+X_expect;
end 

figure(1)
subplot(2,1,1);

for i= 1 :size(X_k,1)
    plot(X_k(i,:));
    hold on
end 
legend("x1 x2");
hold on;


subplot(2,1,2);



for i =1:size(U_k,1)
    plot (U_k(i,:));
    hold on 
end

legend("u");
hold on;
figure(2);


X_exp_vec=zeros(n,k_step);
for k = 1:k_step
    X_exp_vec(:,k)=[10*cos(360/k_step*k)+10;10*sin(360/k_step*k)-5];
end
plot(X_exp_vec(1,:),X_exp_vec(2,:),'g')
hold on;

plot(X_k(1,:),X_k(2,:),'r')
legend("track","reference");

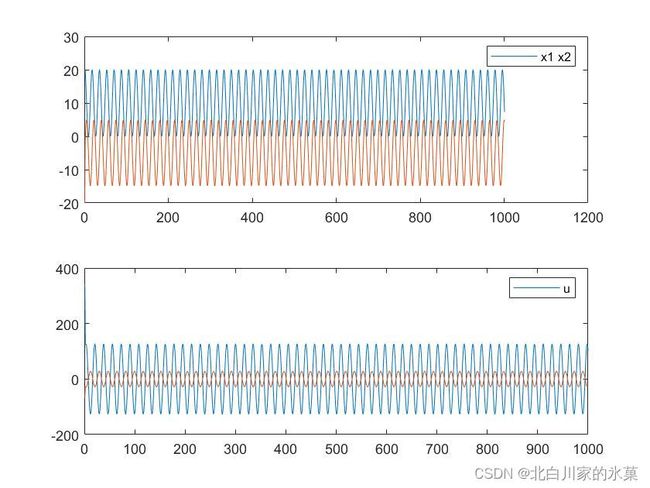
该代码在原基础上加入了约束条件，如果代码运行不了可以将约束去掉，仿真结果如下，其中 权重提高可以提高跟踪的效果

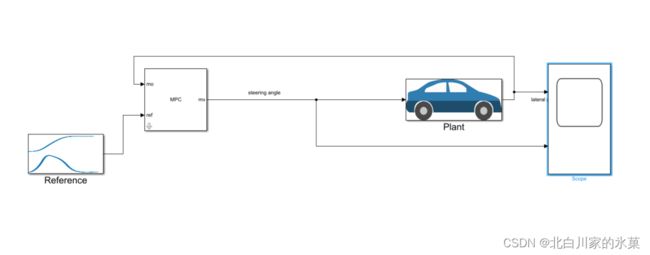
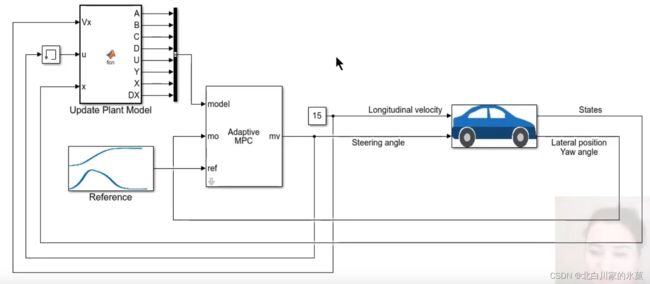
3.基于simulink的仿真

在simulink中使用mpc controler搭建框图如下：

搭建教程： 【Model Predictive Control】了解模型预测控制，第六部分：如何使用 Simulink 和模型预测控制工具箱设计 MPC 控制器_哔哩哔哩_bilibili

给定约束：

① 方向盘物理转角不得超过30°

② 为了保证舒适度，方向盘变化率不得超过15°/s

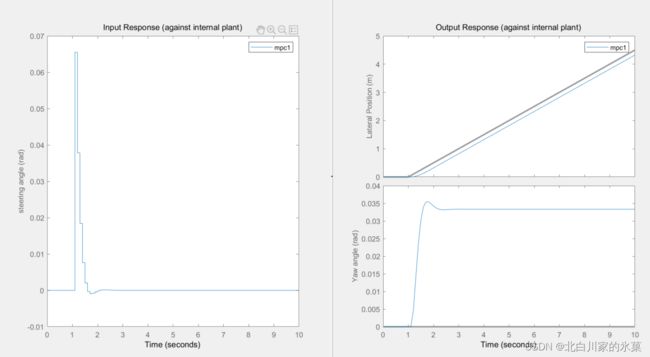
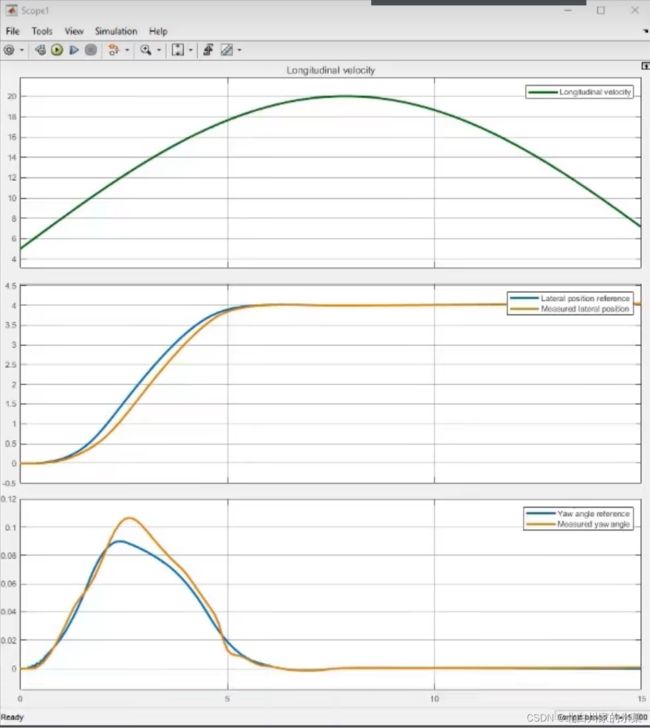
在此条件下，仿真结果如图：

 在预测范围为10，控制范围为2时，结果如下：

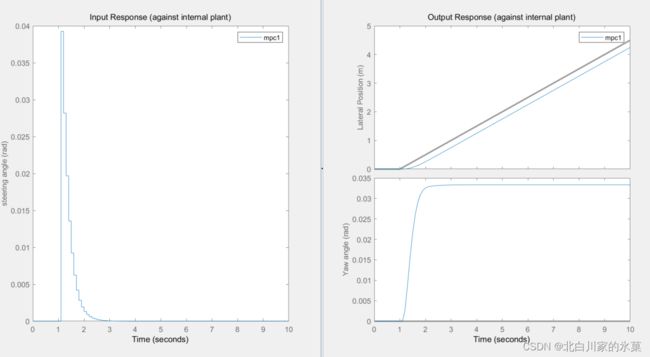
如果将prediction horizon变大，结果如下：

 

超调此时减小了，但是预测范围太大可能会造成算力的浪费

 

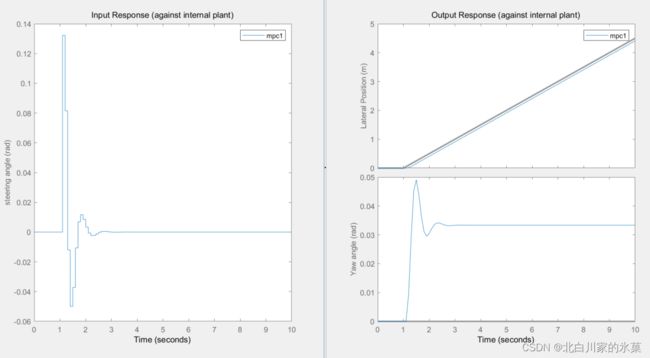
将控制范围变大，可见跟踪效果更好，跟踪曲线更接近reference

 

然而，进一步提高控制范围，发现结果变化并不大，所以我们一般取预测范围的20%-30%就可以了 

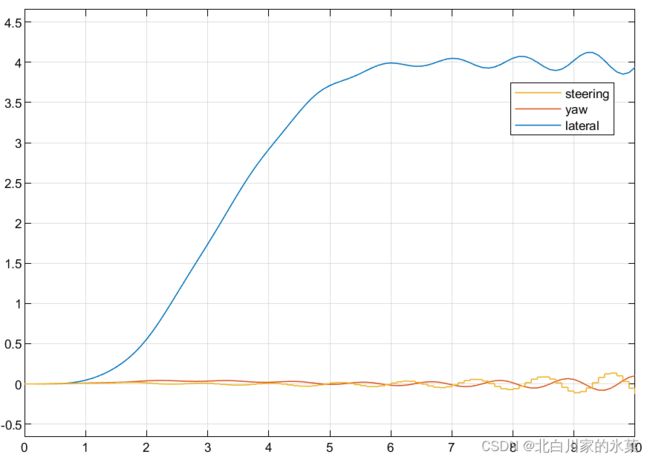
当速度提升至35时，结果如下：

可见跟踪效果并不好，所以我们最好添加自适应MPC（adaptive MPC）

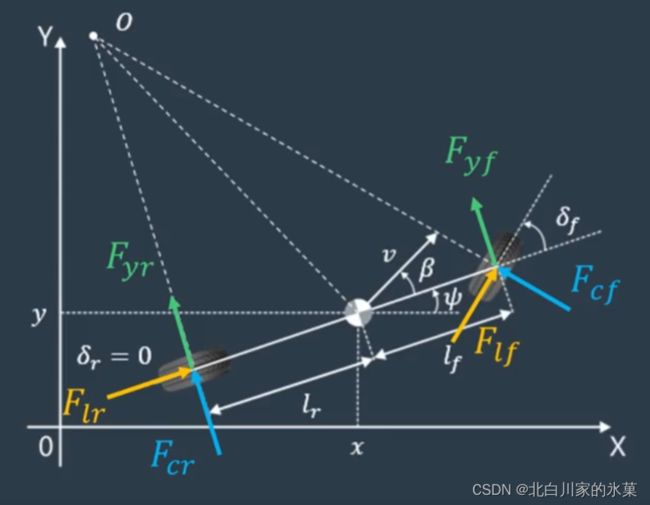
 4.车辆横向运动状态空间模型的推导

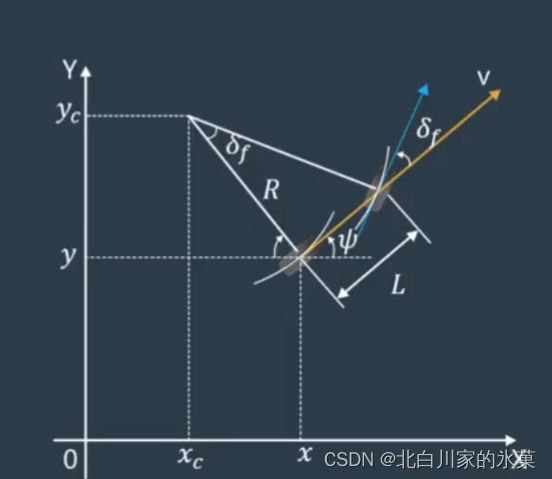
这里就必须要提及著名的自行车模型

自行车模型的条件如下：
① 车辆做平面运动

② 左右前轮的转向角近似相等

③ 忽略轮胎收到的侧向力

④ 忽略前后轴荷载的转移

⑤ 车身和悬架系统是刚性的

其中②  ③限制了车体必须是低速运动的

 我们选择状态变量：

x,y:车辆在绝对坐标系的位置

v：车辆的速度大小

: 车辆的转角大小

假如这是一辆车，则有：

 :前轮与车辆纵轴之间的夹角

 :后轮与车辆纵轴之间的夹角（如果后轮不能转就是0）

 :质心侧偏角，即车辆速度与纵轴之间的偏角，低速行驶时认为特别小

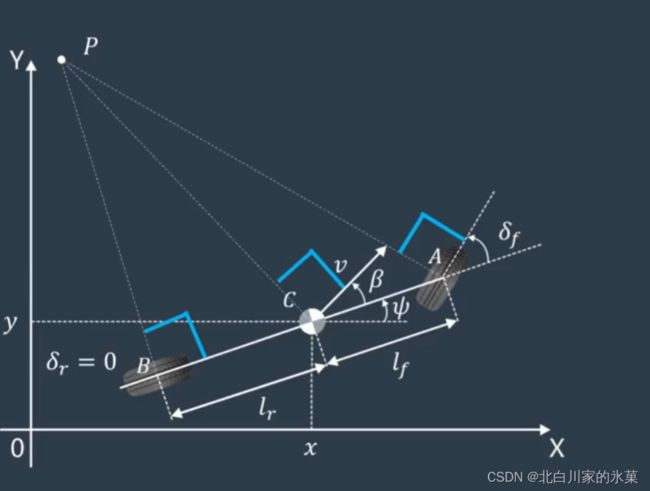
A B为前后轮的速度质心，C为车体整体质心，下面以C为原点推导自行车模型，当然，我们可以以A，B为原点推导，过程相似，结果略有差异

设PC=R

则有：

整理得：

联立以上两式，同时在低速时，我们假设R变化缓慢，那么:

与以上两式联立，得：

在质心处：

此时反解:

在高速情况下，外力对于车辆的影响是比较大的，所以我们不光要考虑运动学模型，更要考虑动力学模型

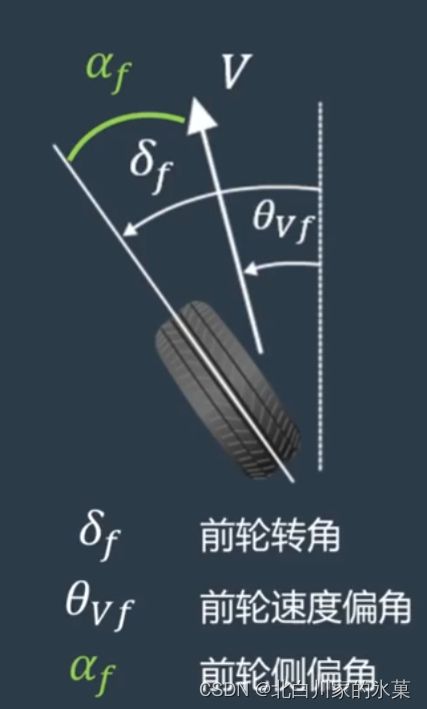
在低速时，我们通常认为轮胎的朝向就是车的运动方向，但是在高速行驶时并不是这样，因为轮胎存在侧偏特性，即车轮的速度方向并不是轮胎的朝向

对于横向动力学模型，有以下假设：

① 忽略悬架运动、道路倾斜度、空气动力学等非线性效应

② 忽略轮胎力的纵横向耦合关系

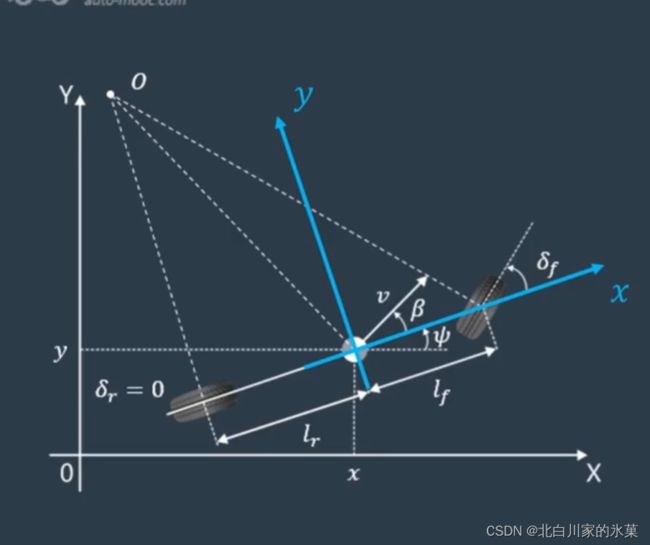
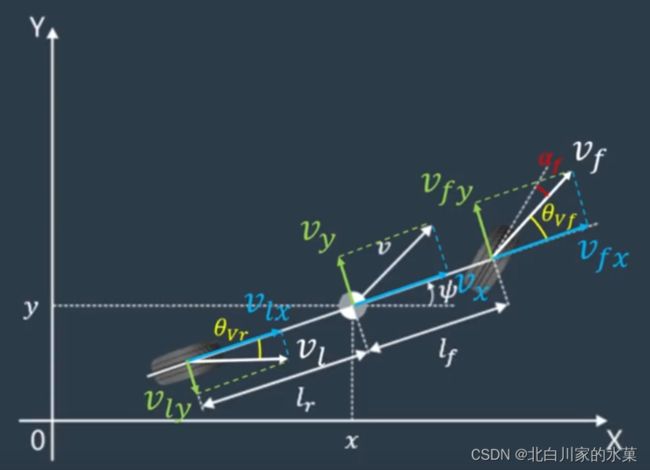
以车体质心为原点，车体纵轴为x轴建立坐标系如下：

 对于侧向，有：

而侧向加速度包括运动加速度和向心加速度

 代入：

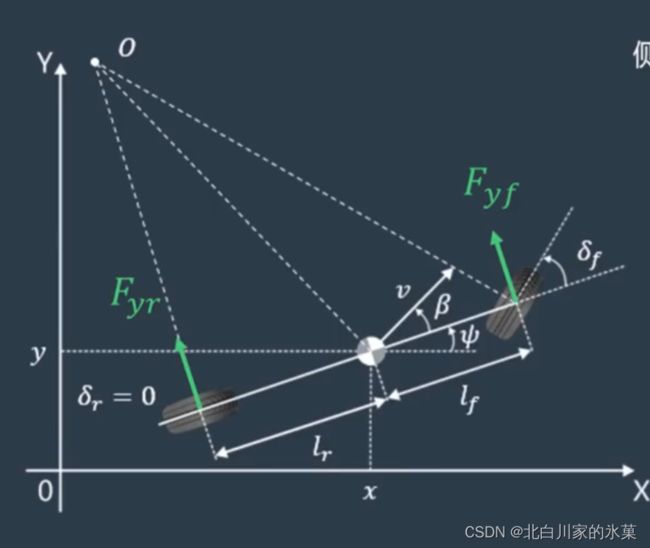
对于横摆运动（即绕z轴的转动）：

对车轮进行受力分析，车轮受侧向力（风吹，提供离心力的摩擦）和纵向力（摩擦，牵引），二者可以合成为车体的横向力 

很小，所以可以忽略

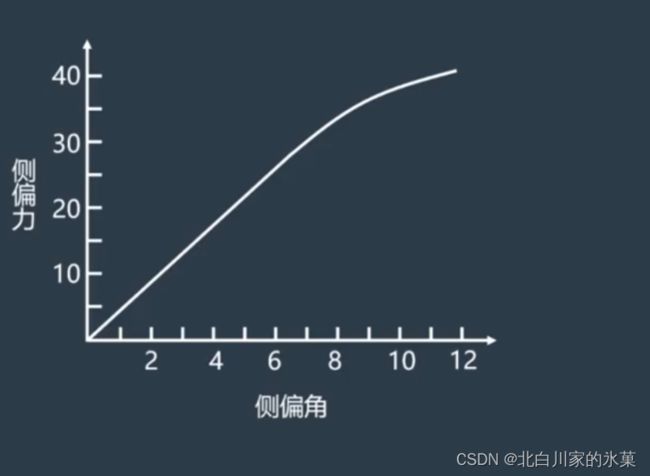
 侧偏力和侧偏角关系如图：

 在侧偏角较小时，可以认为：

其中C为侧偏刚度

因此：

对前后轮进行速度分解，得：

代入侧向力表达式：

代入横向动力学方程，并整理成矩阵形式

令：

      为状态向量

为控制量

 为已知参数

得：

可见，车体的横向运动模型和车的是有关系的

5.自适应MPC

自适应MPC可以在运行的每一步提供一个新的，合适的线性模型，确保在新的运行条件下做出更准确的预测

这个我没做出来，因为属实不知道怎么改这个plant，所以直接截图了

更改的值，甚至可以将其改为正弦信号，结果如下：

 可见MPC的确可以根据不同的模型，不同的条件进行自适应控制

五、多种MPC类型拓展

1.非线性MPC（nonlinear MPC\NMPC）

参考文献：

[PDF] MPC-Based Approach to Active Steering for Autonomous Vehicle Systems | Semantic Scholar

2.线性时变MPC（LTV MPC）

面对非线性模型，我们一般有两个思路：

一个是直接采用非线性模型，对原来模型直接进行控制

另一个是对模型进行连续的在线线性化

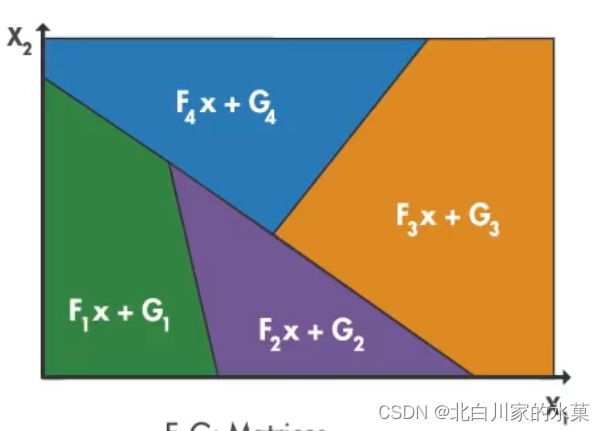
3.Explicit MPC（显式MPC）

参考文献

显式预测控制（Explicit MPC）_dymodi的博客-CSDN博客_显式模型预测控制