EEMD去噪算法

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

提示：这里可以添加本文要记录的大概内容：

例如：随着人工智能的不断发展，机器学习这门技术也越来越重要，很多人都开启了学习机器学习，本文就介绍了机器学习的基础内容。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、EEMD去噪

EEMD方法的本质是一种叠加高斯白噪声的多次经验模式分解，利用了高斯白噪声具有频率均匀分布的统计特性，通过每次加入同等幅值的不同白噪声来改变信号的极值点特性，之后对多次EMD得到的相应IMF进行总体平均来抵消加入的白噪声，从而有效抑制模态混叠的产生。EEMD分解步骤如下：
（1）设定总体平均次数M；
（2）将一个具有标准正态分布的白噪声加到原始信号上，以产生多个新的信号：

式中表示第i次加性白噪声序列，表示第i次试验的附加噪声信号；
（3）对所得含噪声的信号分别进行EMD分解，得到各自和的形式：

式中，为第i次加入白噪声后分解得到的第j个imf；是残余函数；J的IMF数量；

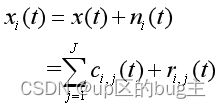
（4）重复步骤(2)和步骤(3)进行M次，每次分解加入幅值不同的白噪声信号得到的集合为：

（5）利用不相关序列的统计平均值为零的原理， 将上述对应的进行集合平均运算，得到EEMD分解后最终的，即：

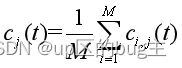
式中是EEMD分解的第j个IMF。

二、使用步骤

1.代码展示

代码如下（示例）：

clc;
clear;
close all;
tic;
%% 产生仿真信号
fs=100;   %数据采样率Hz
t=1:1/fs:4096*1/fs; %对数据进行采样
n = length(t);  %数据的采样数目
f1 =0.25; %信号的频率
f2=0.005;

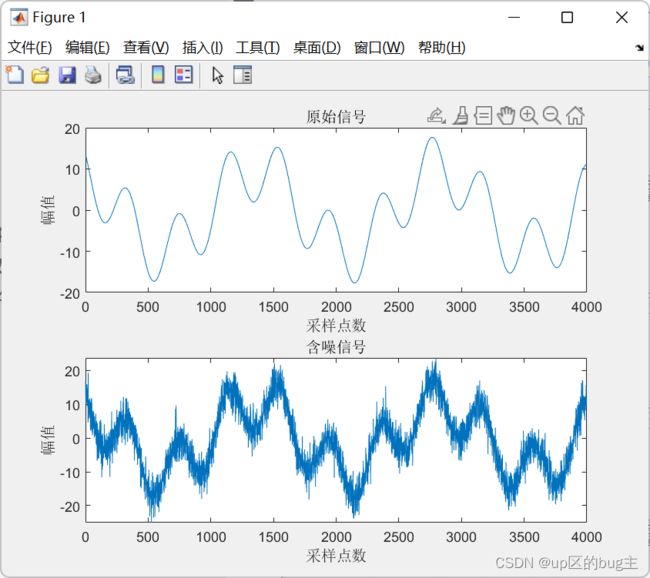
x=8*sin(2*pi*f1*t+cos(2*pi*f2*t))+10*cos(0.43*t);x=x';    %产生原始信号，将其转置为列向量
nt=3*randn(n,1);  %高斯白噪声生成
y=x+nt; %含噪信号

figure(1);
subplot(2,1,1);plot(x);title('原始信号');xlabel('采样点数');ylabel('幅值');
subplot(2,1,2);plot(y);title('含噪信号');xlabel('采样点数');ylabel('幅值');
%% EEMD分解

Nstd=0.2*std(y);
NE=30;
imf=eemd(y,Nstd,NE);
figure(2);
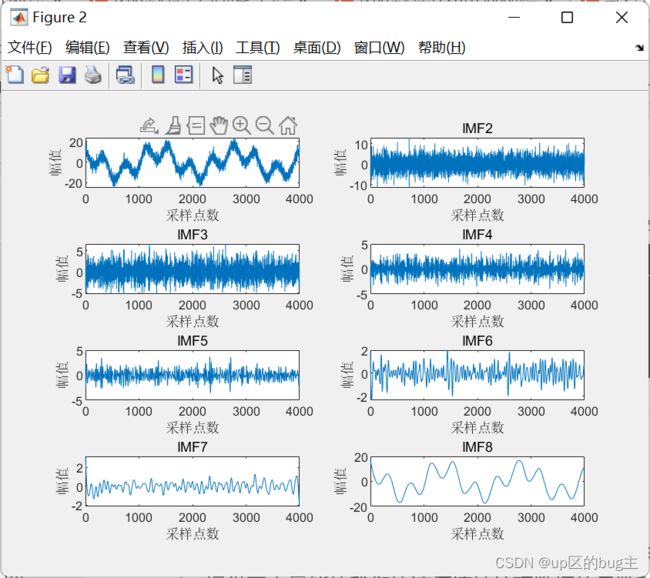
% IMF1是原始输入信号y，IMF2-IMF7是从高频到低频的IMF分量，IMF8是残余分量
subplot(4,2,1); plot(imf(:,1));title('IMF1');xlabel('采样点数');ylabel('幅值');
subplot(4,2,2); plot(imf(:,2));title('IMF2');xlabel('采样点数');ylabel('幅值');
subplot(4,2,3); plot(imf(:,3));title('IMF3');xlabel('采样点数');ylabel('幅值');
subplot(4,2,4); plot(imf(:,4));title('IMF4');xlabel('采样点数');ylabel('幅值');
subplot(4,2,5); plot(imf(:,5));title('IMF5');xlabel('采样点数');ylabel('幅值');
subplot(4,2,6); plot(imf(:,6));title('IMF6');xlabel('采样点数');ylabel('幅值');
subplot(4,2,7); plot(imf(:,7));title('IMF7');xlabel('采样点数');ylabel('幅值');
subplot(4,2,8); plot(imf(:,8));title('IMF8');xlabel('采样点数');ylabel('幅值');
imf=imf(:,2:8);
n=7;
r=zeros(1,n);
for i=1:n
    % 求相关系数
    r(1,i)=sum((y-mean(y)).*(imf(:,i)-mean(imf(:,i))),1)./sqrt(sum(((y-mean(y)).^2),1).*sum(((imf(:,i)-mean(imf(:,i))).^2),1));
end
% 求标准差
d=std(r);
[M,I] = max(r);
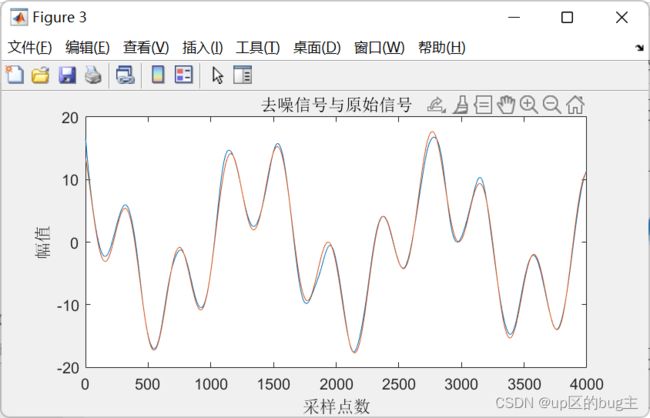
% 信号的重构
yt=imf(:,I);
figure(3);
plot(yt);
hold on;
plot(x);
title('去噪信号与原始信号');xlabel('采样点数');ylabel('幅值');
toc;
% figure(1)
% width=400;%宽度，像素数
% height=250;%高度
% left=200;%距屏幕左下角水平距离
% bottem=100;%距屏幕左下角垂直距离
% set(gcf,'position',[left,bottem,width,height])
% plot(i,afz','-*','LineWidth',2)
% %xlim([0 100]);
%  xlabel('故障宽度 e-3','FontSize',10.5);ylabel('幅值/(m/s^2)','FontSize',10.5)
% title('峰值');

2.function [spmax, spmin, flag]= extrema(in_data)

代码如下（示例）：

% 这是一个用于显著性检验的实用程序.
%
%   function [spmax, spmin, flag]= extrema(in_data)
%
% INPUT:
%       in_data: Inputted data, a time series to be sifted（被筛选）;
% OUTPUT:
%       spmax: The locations (col 1) of the maxima and its corresponding
%              values (col 2)
%       spmin: The locations (col 1) of the minima and its corresponding
%              values (col 2)
%
% References can be found in the "Reference" section.
%
% The code is prepared by Zhaohua Wu. For questions, please read the "Q&A" section or
% contact
%   zwu@fsu.edu
%
function [spmax, spmin, flag]= extrema(in_data)

flag=1;
dsize=length(in_data);

spmax(1,1) = 1;
spmax(1,2) = in_data(1);
jj=2;
kk=2;
while jj<dsize
    if ( in_data(jj-1)<=in_data(jj) && in_data(jj)>=in_data(jj+1) )
        spmax(kk,1) = jj;
        spmax(kk,2) = in_data (jj);
        kk = kk+1;
    end
    jj=jj+1;
end
spmax(kk,1)=dsize;
spmax(kk,2)=in_data(dsize);

if kk>=4
    slope1=(spmax(2,2)-spmax(3,2))/(spmax(2,1)-spmax(3,1));
    tmp1=slope1*(spmax(1,1)-spmax(2,1))+spmax(2,2);
    if tmp1>spmax(1,2)
        spmax(1,2)=tmp1;
    end

    slope2=(spmax(kk-1,2)-spmax(kk-2,2))/(spmax(kk-1,1)-spmax(kk-2,1));
    tmp2=slope2*(spmax(kk,1)-spmax(kk-1,1))+spmax(kk-1,2);
    if tmp2>spmax(kk,2)
        spmax(kk,2)=tmp2;
    end
else
    flag=-1;
end


msize=size(in_data);
dsize=max(msize);
xsize=dsize/3;
xsize2=2*xsize;

spmin(1,1) = 1;
spmin(1,2) = in_data(1);
jj=2;
kk=2;
while jj<dsize
    if ( in_data(jj-1)>=in_data(jj) && in_data(jj)<=in_data(jj+1))
        spmin(kk,1) = jj;
        spmin(kk,2) = in_data (jj);
        kk = kk+1;
    end
    jj=jj+1;
end
spmin(kk,1)=dsize;
spmin(kk,2)=in_data(dsize);

if kk>=4
    slope1=(spmin(2,2)-spmin(3,2))/(spmin(2,1)-spmin(3,1));
    tmp1=slope1*(spmin(1,1)-spmin(2,1))+spmin(2,2);
    if tmp1<spmin(1,2)
        spmin(1,2)=tmp1;
    end

    slope2=(spmin(kk-1,2)-spmin(kk-2,2))/(spmin(kk-1,1)-spmin(kk-2,1));
    tmp2=slope2*(spmin(kk,1)-spmin(kk-1,1))+spmin(kk-1,2);
    if tmp2<spmin(kk,2)
        spmin(kk,2)=tmp2;
    end
else
    flag=-1;
end

flag=1;

---

2.functi代码如下（示例）：

function allmode=eemd(Y,Nstd,NE)
xsize=length(Y);
dd=1:1:xsize; 
Ystd=std(Y);
Y=Y/Ystd;    

%part2.evaluate TNM as total IMF number,ssign 0 to N*TNM2 matrix
TNM=fix(log2(xsize))-5;   % TNM=m
TNM2=TNM+2;               
for kk=1:1:TNM2
    for ii=1:1:xsize
        allmode(ii,kk)=0.0;  
    end
end

%part3 Do EEMD -----EEMD loop start
for iii=1:1:NE %EEMD loop NE times EMD sum together

%part4 --Add noise to original data,we have X1
    for i=1:xsize
        temp=randn(1,1)*Nstd; % add a random noise to Y
        X1(i)=Y(i)+temp;
    end

%part4 --assign original data in the first column
    for jj=1:1:xsize
        mode(jj,1) = Y(jj); % assign Y to column 1of mode
    end

%part5--give initial 0to xorigin and xend
    xorigin = X1;   % 
    xend = xorigin; %

%part6--start to find an IMF-----IMF loop start
    nmode = 1;

    while nmode <= TNM
    xstart = xend; %last loop value assign to new iteration loop
                   %xstart -loop start data
    iter = 1;      %loop index initial value

%part7--sift 10 times to get IMF---sift loop start
        while iter<=10 
            [spmax, spmin, flag]=extrema(xstart); %call function extrema
                                                  %the usage of spline ,please see part11.
            upper= spline(spmax(:,1),spmax(:,2),dd); %upper spline bound of this sift
            lower= spline(spmin(:,1),spmin(:,2),dd); %lower spline bound of this sift
            mean_ul = (upper + lower)/2;            %spline mean of upper and lower
            xstart = xstart - mean_ul;              %extract spline mean from Xstart
            iter = iter +1;
        end

%part8--subtract IMF from data ,then let the residual xend to start to find next IMF
    xend = xend - xstart;      
    nmode=nmode+1;              

%part9--after sift 10 times,that xstart is this time IMF
    for jj=1:1:xsize
        mode(jj,nmode) = xstart(jj);  
    end
end

%part10--after gotten all(TNM) IMFs ,the residual xend is over all trend
% put them in the last column
    for jj=1:1:xsize
        mode(jj,nmode+1)=xend(jj);
    end

%after part 10 ,original + TNM IMFs+overall trend ---those are all in mode
    allmode=allmode+mode;   
end  %part3 Do EEMD -----EEMD loop end

%part11--devide EEMD summation by NE,std be multiply back to data
allmode=allmode/NE;    
allmode=allmode*Ystd;  

---

结果展示

。