西瓜书笔记6:支持向量机

目录

6.1 间隔与支持向量

6.2 对偶问题

求解w

求解b

6.3 核函数

非线性映射

核函数

6.4 软间隔与正则化

软间隔

参数求解

正则化

6.5 支持向量回归

6.6 核方法

---

6.1 间隔与支持向量

分类学习基本想法: 就是基于训练集D在样本空间中找到一个划分超平面、将

不同类别的样本分开.

超平面(w,b)的线性方程:

$$ \boldsymbol{w}^T\boldsymbol{x}+b=0\\ 其中\boldsymbol{w}=(w_1;\cdots ;w_d)为法向量,\\ b为位移项(面与原点距离) $$

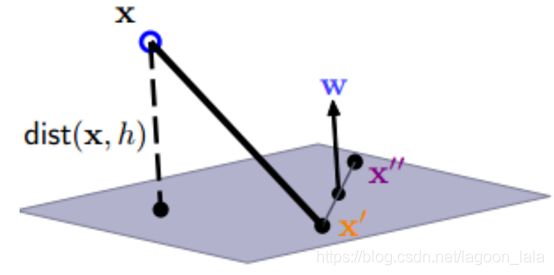
样本空间中点x到超平面(w,b)距离:

$$ r=\frac{|\boldsymbol{w}^T\boldsymbol{x}+b|}{||\boldsymbol{w}||} $$

推导参考: https://blog.csdn.net/jbb0523 点到面距离=点面连线(x-x')在法向量投影 x'为超平面上的点, 所以满足: $$ \boldsymbol{w}^T\boldsymbol{x}'+b=0\\ b=-\boldsymbol{w}^T\boldsymbol{x}' $$ 代入b可定义法向量w与点面连线(x-x')的内积为: $$ \boldsymbol{w}^T(\boldsymbol{x}-\boldsymbol{x}')\\ =\boldsymbol{w}^T\boldsymbol{x}-\boldsymbol{w}^T\boldsymbol{x}'\\ =\boldsymbol{w}^T\boldsymbol{x}+b $$ 根据投影公式: $$ |\boldsymbol{a}|\cos\theta=\frac{a\cdot b}{|b|} $$ 投影公式代入线(x-x')与法向量w, 并根据其内积化简: $$ r=\frac{|\boldsymbol{w}^T(\boldsymbol{x}-\boldsymbol{x}')|}{||\boldsymbol{w}||}=\frac{|\boldsymbol{w}^T\boldsymbol{x}+b|}{||\boldsymbol{w}||} $$

假设超平面(w,b)对所有样本分类正确, 即:

$$ \left\{\begin{array}1 (\boldsymbol{w'})^T\boldsymbol{x}_i+b'>0, &y_i=+1\\ (\boldsymbol{w'})^T\boldsymbol{x}_i+b'<0, &y_i=-1\\ \end{array}\right. $$

考虑两类样本之间存在间隔, 只对不在间隔内的样本分类:

$$ \left\{ \begin{array}{1} (\boldsymbol{w'})^T\boldsymbol{x}_i+b'\geq\zeta, &y_i=+1\\ (\boldsymbol{w'})^T\boldsymbol{x}_i+b'\leq-\zeta, &y_i=-1\\ \end{array} \right. $$

对参数做缩放变换:

$$ 令\boldsymbol{w}=\frac{\boldsymbol{w'}}{\zeta},b=\frac{b'}{\zeta}\\ \left\{\begin{array}1 (\boldsymbol{w})^T\boldsymbol{x}_i+b\geq 1, &y_i=+1\\ (\boldsymbol{w})^T\boldsymbol{x}_i+b\leq -1, &y_i=-1\\ \end{array}\right. $$

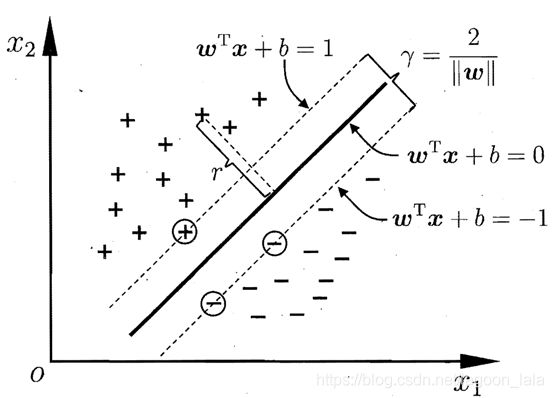
支持向量: 距离超平面最近的几个训练样本对应特征向量, 使上不等式中等号成立.

间隔(margin): ，两个异类支持向量到超平面的距离之和: 

$$ \gamma=\frac{2}{||\boldsymbol{w}||} $$

“最大间隔”的划分超平面分类结果最鲁棒，泛化能力最强.

所求最优划分平面需满足 1. 间隔最大(目标函数) 2.正确分类所有样本(约束条件)

$$ \max_{\boldsymbol{w},b}\frac{2}{||\boldsymbol{w}||}\\ \mathrm{s.t.}~~y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)\geq 1, i=1,2,\cdots ,m $$

转为最小化问题(正则化)即得支持向量机SVM (Support Vector Machine)基本型:

$$ \min_{\boldsymbol{w},b}\frac{1}{2}||\boldsymbol{w}||^2\\ \mathrm{s.t.}~~y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)\geq 1, i=1,2,\cdots ,m $$

6.2 对偶问题

对偶问题的详细理解可参考: https://www.bilibili.com/video/BV1HP4y1Y79e?p=1 最优化可参考中国科学院大学研究生院凌清的<最优化理论>

希望求解上式(最小化问题, SVM基本型)得划分超平面(w,b)所对应的模型:

$$ f(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+b $$

用拉格朗日乘子法得到SVM基本型的对偶问题(dual problem)的拉格朗日函数:

$$ L(\boldsymbol{w},b,\boldsymbol{\alpha}) = \frac{1}{2}||\boldsymbol{w}||^2+\sum_{i=1}^m\alpha_i(1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)) \\ 其中\boldsymbol{\alpha}=(\alpha_1;\cdots ;\alpha_m) $$

推导: SVM基本型的约束条件为: $$ y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)\geq 1, i=1,2,\cdots ,m $$ 为使用拉格朗日乘子法条件函数需要转化为: $$ g(x)=1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)\leq 0 $$ 引入拉格朗日乘子得: $$ \begin{aligned} L(\boldsymbol{w},b,\boldsymbol{\alpha}) &= \frac{1}{2}||\boldsymbol{w}||^2+\sum_{i=1}^m\alpha_i(1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)) \\ & = \frac{1}{2}||\boldsymbol{w}||^2+\sum_{i=1}^m(\alpha_i-\alpha_iy_i \boldsymbol{w}^T\boldsymbol{x}_i-\alpha_iy_ib)\\ & =\frac{1}{2}\boldsymbol{w}^T\boldsymbol{w}+\sum_{i=1}^m\alpha_i -\sum_{i=1}^m\alpha_iy_i\boldsymbol{w}^T\boldsymbol{x}_i-\sum_{i=1}^m\alpha_iy_ib \end{aligned} $$

相关知识: 拉格朗日乘子法

参考:

http://www.csc.kth.se/utbildning/kth/kurser/DD3364/Lectures/Duality.pdf

对于原始问题:

$$ \min_x f(x),\mathrm{s.t.}~h(x)=0,g(x)\leq 0 $$

拉格朗日乘子法将有约束优化问题转化为无约束优化问题

其步骤:

1. 优化问题的拉格朗日函数

$$ L(x,\lambda,\mu)=f(x)+\lambda h(x)+\mu g(x) $$

2. L对x求导, 令导数为0可解得x关于λ, μ的式子

$$ \frac{\partial L(x,\lambda,\mu)}{\partial x}=0 $$

3. 代入λ, μ消x:

$$ \Gamma(\lambda,\mu)=\min_x L(x,\lambda,\mu) $$

4. 即得对偶问题

$$ \max_{\lambda,\mu}\Gamma(\lambda,\mu) $$

令L(w,b,α)对w和b的偏导为零可得:

$$ \boldsymbol{w} = \sum_{i=1}^m\alpha_iy_i\boldsymbol{x}_i\\ 0=\sum_{i=1}^m\alpha_iy_i $$

推导: $$ \frac {\partial L}{\partial \boldsymbol{w}}=\frac {\partial \frac{1}{2}\boldsymbol{w}^T\boldsymbol{w}}{\partial \boldsymbol{w}}+\frac {\partial \sum_{i=1}^m\alpha_i}{\partial \boldsymbol{w}} -\frac {\partial \sum_{i=1}^m\alpha_iy_i\boldsymbol{w}^T\boldsymbol{x}_i}{\partial \boldsymbol{w}}-\frac {\partial \sum_{i=1}^m\alpha_iy_ib}{\partial \boldsymbol{w}} \\  =\frac{1}{2}\times2\times\boldsymbol{w} + 0 - \sum_{i=1}^{m}\alpha_iy_i \boldsymbol{x}_i-0= 0 \\ \Longrightarrow \boldsymbol{w}=\sum_{i=1}^{m}\alpha_iy_i \boldsymbol{x}_i $$ 其中根据矩微分公式: $$ \cfrac{\partial\boldsymbol{a}^{\mathrm{T}}\boldsymbol{x}}{\partial\boldsymbol{x}}=\cfrac{\partial\boldsymbol{x}^{\mathrm{T}}\boldsymbol{a}}{\partial\boldsymbol{x}}=\boldsymbol{a} $$ 先将左边因子看作a, 再将右边因子看作a得: $$ \frac {\partial \boldsymbol{w}^T\boldsymbol{w}}{\partial \boldsymbol{w}}=2\boldsymbol{w} $$ 对b求导过程: $$ \frac {\partial L}{\partial b}=0+0-0-\sum_{i=1}^{m}\alpha_iy_i=0\\ \Longrightarrow \sum_{i=1}^{m}\alpha_iy_i=0 $$

将导数为0所得两式，代入L中消去w, b, 且约束对b导数为0所得式子&拉格朗日乘子非负 ，得对偶问题:

$$ \begin{aligned} \max_{\boldsymbol{\alpha}} & \sum_{i=1}^m\alpha_i - \frac{1}{2}\sum_{i = 1}^m\sum_{j=1}^m\alpha_i \alpha_j y_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j \\ \text { s.t. } & \sum_{i=1}^m \alpha_i y_i =0 \\ & \alpha_i \geq 0 \quad i=1,2,\dots ,m \end{aligned} $$

其中, 两个求和项相乘即将每一项均分别对应相乘一遍即可；因为有两个不同的求和，所以使用两个求和变量i, j.

$$ \begin{aligned} \inf_{\boldsymbol{w},b} L(\boldsymbol{w},b,\boldsymbol{\alpha}) &=\frac{1}{2}\boldsymbol{w}^T\boldsymbol{w}+\sum_{i=1}^m\alpha_i -\sum_{i=1}^m\alpha_iy_i\boldsymbol{w}^T\boldsymbol{x}_i-\sum_{i=1}^m\alpha_iy_ib \\ &=\frac {1}{2}\boldsymbol{w}^T\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i-\boldsymbol{w}^T\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i+\sum _{i=1}^m\alpha_ i -b\sum _{i=1}^m\alpha_iy_i \\ & = -\frac {1}{2}\boldsymbol{w}^T\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i+\sum _{i=1}^m\alpha_i -b\cdot 0\\ & = -\frac {1}{2}\boldsymbol{w}^T\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i+\sum _{i=1}^m\alpha_i \\ &=-\frac {1}{2}(\sum_{i=1}^{m}\alpha_iy_i\boldsymbol{x}_i)^T(\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i)+\sum _{i=1}^m\alpha_i \\ &=-\frac {1}{2}\sum_{i=1}^{m}\alpha_iy_i\boldsymbol{x}_i^T\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i+\sum _{i=1}^m\alpha_i \\ &=\sum _{i=1}^m\alpha_i-\frac {1}{2}\sum_{i=1 }^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j \end{aligned} $$

求解w

模型中代入w为:

$$ \begin{aligned} f(\boldsymbol{x})&=\boldsymbol{w}^T\boldsymbol{x}+b\\  &=\sum_{i=1}^m\alpha_iy_i\boldsymbol{x}^T_i\boldsymbol{x}+b \end{aligned} $$

其中, x为待预测的示例，x_i为训练集中的示例(训练完成后大部分的训练样本都不需保留，最终模型仅与支持向量有关), 拉格朗日乘子α_i根据SMO(Sequential Minmal Optimization)算法求得.

SVM基本型的不等式约束对应KKT(Karush-Kuhn-Tucker)条件

$$ \left\{\begin{array}{l}\alpha_{i} \geq 0 \\ y_{i} f\left(\boldsymbol{x}_{i}\right)-1 \geq 0 \\ \alpha_{i}\left(y_{i} f\left(\boldsymbol{x}_{i}\right)-1\right)=0\end{array}\right. $$

其含义为极值点要么位于约束区域内部(a_i=0), 要么位于约束区域边缘(yf(x)-1=0). 且目标函数梯度方向朝向区域内部, 约束函数的梯度方向朝向约束区域外部:

求解对偶问题使用SMO算法:

1. 选取一对需更新的变量α_i和α_j;

2. 固定α_i和α_j以外的参数，求解对偶问题式获得更新后的α_i和α_j.

SMO先选取违背 KKT程度最大的变量, 第二个变量为了使目标函数值减小最快，选取两变量所对应样本之间的间隔最大的变量. 仅考虑α_i和α_j时，重写对偶问题约束:

$$ \sum_{i=1}^m \alpha_i y_i =0,\alpha_i\geq 0\\ \Rightarrow \alpha_i y_i+\alpha_j y_j=c,\alpha_i\geq 0,\alpha_j\geq 0 $$

其中c为保证原约束成立的常数

$$ c=-\sum_{k\neq i,j} \alpha_k y_k $$

利用该约束消去α_j, 可得单变量α_i的二次规划.

求解b

b的求解办法: 代入支持向量(x_s, y_s), 由于支持向量都在间隔边缘, f=1时y=1; f=-1时y=-1, 可表示为:

$$ y_s f(\boldsymbol{x}_s)=1\\ \Rightarrow y_s\left(\sum_{i\in S}\alpha_iy_i\boldsymbol{x}^T_i\boldsymbol{x}_s+b\right)=1 $$

一般为避免误差, 使用所有支持向量求解的平均值:

$$ b=\frac{1}{|S|}\sum_{s\in S} \left(y_s-\sum_{i\in S}\alpha_iy_i\boldsymbol{x}^T_i\boldsymbol{x}_s\right) $$

其中|S|代表支持向量个数

$$ S=\{i|\alpha_i>0,i=1,\cdots,m\} $$

6.3 核函数

非线性映射

对于非线性可分问题(如'异或')映射到更高维的特征空间，使之线性可分.

Φ(x)表示映射后的特征向量，此时特征空间的划分超平面的模型(其中w维度与Φ(x)同):

$$ f(\boldsymbol{x})=\boldsymbol{w}^T\phi(\boldsymbol{x})+b $$

解最大化间隔的参数, 即SVM:

$$ \min_{\boldsymbol{w},b}\frac{1}{2}||\boldsymbol{w}||^2\\ \mathrm{s.t.}~~y_i(\boldsymbol{w}^T\phi(\boldsymbol{x}_i)+b)\geq 1, i=1,2,\cdots ,m $$

对偶问题:

$$ \begin{aligned} \max_{\boldsymbol{\alpha}} & \sum_{i=1}^m\alpha_i - \frac{1}{2}\sum_{i = 1}^m\sum_{j=1}^m\alpha_i \alpha_j y_iy_j\phi(\boldsymbol{x}_i)^T\phi(\boldsymbol{x}_j) \\ \text { s.t. } & \sum_{i=1}^m \alpha_i y_i =0 \\ & \alpha_i \geq 0 \quad i=1,2,\dots ,m \end{aligned} $$

核技巧: 计算Φ(x)^T*Φ(x)困难, 看作x_i, x_j在原样本空间通过函数κ计算结果.

$$ \kappa(\boldsymbol{x}_i, \boldsymbol{x}_j)=\left<\phi(\boldsymbol{x}_i),\phi(\boldsymbol{x}_j)\right>=\phi(\boldsymbol{x}_i)^T\phi(\boldsymbol{x}_j) $$

即核函数分解为两形式相同向量的内积.

代入核函数k重写对偶问题:

$$ \begin{aligned} \max_{\boldsymbol{\alpha}} & \sum_{i=1}^m\alpha_i - \frac{1}{2}\sum_{i = 1}^m\sum_{j=1}^m\alpha_i \alpha_j y_iy_j\kappa (\boldsymbol{x}_i,\boldsymbol{x}_j) \\ \text { s.t. } & \sum_{i=1}^m \alpha_i y_i =0 \\ & \alpha_i \geq 0 \quad i=1,2,\dots ,m \end{aligned} $$

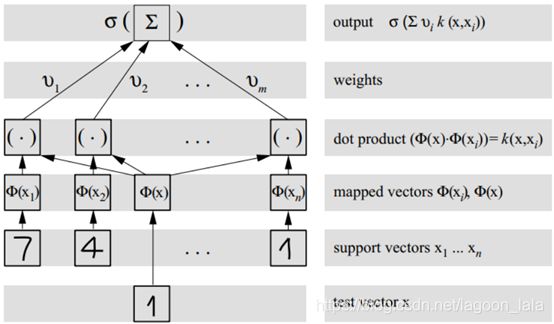
所得超平面模型最优解通过训练样本的核函数展开, 即"支持向量展式 "(support vector expansion):

$$ \begin{aligned} f(\boldsymbol{x})&=\boldsymbol{w}^T\boldsymbol{x}+b\\  &=\sum_{i=1}^m\alpha_iy_i\phi(\boldsymbol{x}_i)^T\phi(\boldsymbol{x})+b\\ &=\sum_{i=1}^m\alpha_iy_i\kappa (\boldsymbol{x}_i,\boldsymbol{x})+b \end{aligned} $$

该式也可看作特征转换后线性分类.

其结构类似RBF径向基函数网络，若将隐层神经元数设置为训练样本数，且每个训练样本对应一个神经元中心，则以高斯径向基函数为激活函数的RBF网络(5.5.1节)恰与高斯核 SVM 的预测函数相同.

核函数

核函数(kernel function)定理:输入空间χ, 对称函数κ()定义在χ*χ. κ为核函数当且仅当"核矩阵" (kernel matrix)K总是半正定的(对称函数对应半正定核矩阵，就能作核函数用):

$$ \mathbf{K}=\left[ \begin{array}{cccc} \kappa\left(\boldsymbol{x}_1, \boldsymbol{x}_1\right) & \cdots &\kappa\left(\boldsymbol{x}_1, \boldsymbol{x}_j\right) & \cdots &\kappa\left(\boldsymbol{x}_1, \boldsymbol{x}_m\right)\\ \vdots & \ddots &\vdots & \ddots & \vdots \\ \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}_1\right) &  \cdots &\kappa\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right) &  \cdots &\kappa\left(\boldsymbol{x}_i, \boldsymbol{x}_m\right) \\  \vdots & \ddots &\vdots & \ddots & \vdots \\ \kappa\left(\boldsymbol{x}_m, \boldsymbol{x}_1\right) & \cdots & \kappa\left(\boldsymbol{x}_m, \boldsymbol{x}_j\right) &  \cdots &\kappa\left(\boldsymbol{x}_m, \boldsymbol{x}_m\right) \\ \end{array} \right] $$

几种常用的核函数:

名称	表达式	参数
线性核	$$ \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right)=\boldsymbol{x}_i ^T\boldsymbol{x}_j $$
多项式核	$$ \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right)=(\boldsymbol{x}_i ^T\boldsymbol{x}_j)^d $$	d≥1为多项式的次数
高斯核	$$ \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right)=e^{-\frac{||\boldsymbol{x}_i-\boldsymbol{x}_j||^2}{2\sigma^2}} $$	σ>0为带宽width
拉普拉斯核	$$ \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right)=e^{-\frac{||\boldsymbol{x}_i-\boldsymbol{x}_j||}{\sigma}} $$	σ>0
Sigmoid核	$$ \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}_j\right)=\tanh(\beta \boldsymbol{x}_i ^T\boldsymbol{x}_j+\theta) $$	tanh为双曲正切函数, β>0, θ<0

文本数据常用线性核，情况不明先试高斯核.

核函数组合仍为核函数:

1. 线性组合

$$ \gamma_1\kappa_1+\gamma_2\kappa_2 $$

2. 直积

$$ \kappa_1\otimes\kappa_2(\boldsymbol{x},\boldsymbol{z})=\kappa_1(\boldsymbol{x},\boldsymbol{z})\kappa_2(\boldsymbol{x},\boldsymbol{z}) $$

3. 任意函数g(x)

$$ \kappa(\boldsymbol{x},\boldsymbol{z})=g(\boldsymbol{x})\kappa_1(\boldsymbol{x},\boldsymbol{z})g(\boldsymbol{z}) $$

6.4 软间隔与正则化

软间隔

"软间隔" (soft margin)允许SVM在样本出错, 缓解非线性可分与过拟合问题.

"硬间隔" (hard margin) 所有样本均在间隔边界外侧, 即样本都必须划分正确;

软间隔(既允许样本越过间隔边界, 也允许样本越过划分超平面), 即允许某些样本不满足约束:

$$ y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)\geq 1 $$

同时考虑1. 最大化间隔; 2. 最小化不满足约束的损失.

得优化目标:

$$ \min _{\boldsymbol{w}, b} \frac{1}{2}\|\boldsymbol{w}\|^{2}+C \sum_{i=1}^{m} \ell_{0/1} (y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)-1) $$

其中常数C>0, l为0/1损失函数:

$$ \ell_{0/1} (z)=\left\{\begin{array}{l} 1,& if~z<0;\\0,& otherwise. \end{array}\right.  $$

C越大, 越重视分类正确, 间隔小; C越小, 则更允许样本越过间隔边界, 间隔大.

0/1损失函数不易解, 常用凸连续函数作为"替代损失" (surrogate loss):

1. hinge损失:

$$ \ell_{hinge} (z)=\max(0,1-z) $$

2. 指数损失:

$$ \ell_{exp} (z)=e^{-z} $$

3. 对率损失:

$$ \ell_{log} (z)=\log(1+e^{-z})=\ln(1+e^{-z}) $$

hinge损失代入优化目标:

$$ \min _{\boldsymbol{w}, b} \frac{1}{2}\|\boldsymbol{w}\|^{2}+C \sum_{i=1}^{m} \max(0,1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)) $$

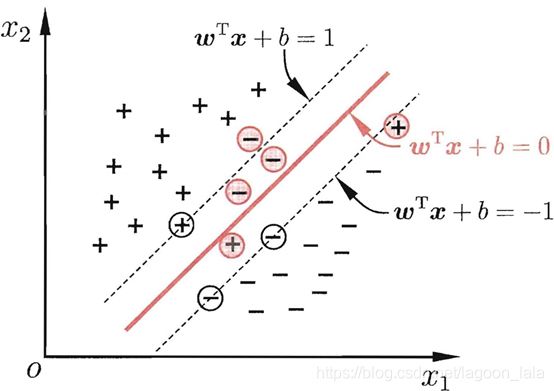
定义"松弛变量" (slack variables)ξ≥0, ξ_i表示样本i不满足间隔边缘约束的程度. 简化上式得"软间隔支持向量机":

$$ \begin{aligned} \min _{\boldsymbol{w}, b, \xi_{i}} & \frac{1}{2}\|\boldsymbol{w}\|^{2}+C \sum_{i=1}^{m} \xi_{i} \\ \text { s.t. } & y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right) \geq 1-\xi_{i} \\ & \xi_{i} \geq 0, i=1,2, \ldots, m \end{aligned} $$

其中约束条件推导:

令

$$ \max \left(0,1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)\right)=\xi_{i} $$

有

$$ \xi_i=\left\{\begin{array}{l} 1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right),& if~1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)>0;\\ 0,& if~1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)\leq0. \end{array}\right.  $$

所以

$$ 1-y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right)\leq\xi_i\\ \Rightarrow y_{i}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_{i}+b\right) \geq 1-\xi_{i} $$

参数求解

通过拉格朗日乘子法, 可得到软间隔支持向量机优化目标的拉格朗日函数, 拉格朗日乘子为α_i, μ_i≥0:

$$ L(\boldsymbol{w},b,\boldsymbol{\alpha},\boldsymbol{\xi},\boldsymbol{\mu}) =\frac{1}{2}||\boldsymbol{w}||^2+C\sum_{i=1}^m \xi_i+\sum_{i=1}^m \alpha_i(1-\xi_i-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b))-\sum_{i=1}^m\mu_i \xi_i $$

令L对w, b, ξ_i偏导为零可得:

$$ \boldsymbol{w}=\sum_{i=1}^{m}\alpha_{i}y_{i}\boldsymbol{x}_{i}\\ 0=\sum_{i=1}^{m}\alpha_{i}y_{i}\\ C=\alpha_i +\mu_i $$

其中前两个式子分别为对w, b求导数为零结果, C为对ξ_i求导:

$$ \begin{aligned}\frac{\partial L}{\partial \xi_i}&=\frac{1}{2}\frac{\partial ||\boldsymbol{w}||^2}{\partial \xi_i}+C\frac{\partial \sum_{i=1}^m \xi_i}{\partial \xi_i}+\frac{\partial \sum_{i=1}^m \alpha_i(1-\xi_i-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b))}{\partial \xi_i}-\frac{\partial \sum_{i=1}^m\mu_i \xi_i}{\partial \xi_i}\\&=0+C \times 1 - \alpha_i \times 1-\mu_i \times 1 =0\\ &\Longrightarrow C=\alpha_i +\mu_i\end{aligned} $$

将偏导为0的三个式子代入拉格朗日函数得对偶问题:

$$ \begin{aligned} \max_{\boldsymbol{\alpha}}&\sum _{i=1}^m\alpha_i-\frac {1}{2}\sum_{i=1 }^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j \\ s.t. &\sum_{i=1}^m \alpha_i y_i=0 \\ & 0 \leq\alpha_i \leq C \quad i=1,2,\dots ,m \end{aligned} $$

先对L代入化简, 将L分成与ξ有关和无关的项, ξ无关的项和硬间隔对偶问题一样处理, ξ有关的项代入C可消:

$$ \begin{aligned} &\frac{1}{2}||\boldsymbol{w}||^2+C\sum_{i=1}^m \xi_i+\sum_{i=1}^m \alpha_i(1-\xi_i-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b))-\sum_{i=1}^m\mu_i \xi_i \\ =&\frac{1}{2}||\boldsymbol{w}||^2+\sum_{i=1}^m\alpha_i(1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b))+C\sum_{i=1}^m \xi_i-\sum_{i=1}^m \alpha_i \xi_i-\sum_{i=1}^m\mu_i \xi_i \\ =&-\frac {1}{2}\sum_{i=1}^{m}\alpha_iy_i\boldsymbol{x}_i^T\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i+\sum _{i=1}^m\alpha_i +\sum_{i=1}^m C\xi_i-\sum_{i=1}^m \alpha_i \xi_i-\sum_{i=1}^m\mu_i \xi_i \\ =&-\frac {1}{2}\sum_{i=1}^{m}\alpha_iy_i\boldsymbol{x}_i^T\sum _{i=1}^m\alpha_iy_i\boldsymbol{x}_i+\sum _{i=1}^m\alpha_i +\sum_{i=1}^m (C-\alpha_i-\mu_i)\xi_i \\ =&\sum _{i=1}^m\alpha_i-\frac {1}{2}\sum_{i=1 }^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j\\ =&\min_{\boldsymbol{w},b,\boldsymbol{\xi}}L(\boldsymbol{w},b,\boldsymbol{\alpha},\boldsymbol{\xi},\boldsymbol{\mu}) \end{aligned} $$

求最优解得对偶问题:

$$ \begin{aligned} \max_{\boldsymbol{\alpha},\boldsymbol{\mu}} \min_{\boldsymbol{w},b,\boldsymbol{\xi}}L(\boldsymbol{w},b,\boldsymbol{\alpha},\boldsymbol{\xi},\boldsymbol{\mu})&=\max_{\boldsymbol{\alpha},\boldsymbol{\mu}}\sum _{i=1}^m\alpha_i-\frac {1}{2}\sum_{i=1 }^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j \\ &=\max_{\boldsymbol{\alpha}}\sum _{i=1}^m\alpha_i-\frac {1}{2}\sum_{i=1 }^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j \end{aligned} $$

其约束条件由0≤α_i, 0≤μ_i代入C=α_i+μ_i得0≤α_i≤C

软硬间隔对偶问题差别:

软间隔约束0≤α_i≤C

硬间隔约束0≤α_i

求解对偶问题可引入核函数得支持向量展式:

$$ \begin{aligned} f(\boldsymbol{x})&=\boldsymbol{w}^T\boldsymbol{x}+b\\  &=\sum_{i=1}^m\alpha_iy_i\phi(\boldsymbol{x}_i)^T\phi(\boldsymbol{x})+b\\ &=\sum_{i=1}^m\alpha_iy_i\kappa (\boldsymbol{x}_i,\boldsymbol{x})+b \end{aligned} $$

KKT条件:

$$ \left\{\begin{array}{l}\alpha_{i} \geq 0, \quad \mu_{i} \geq 0 \\ y_{i} f\left(\boldsymbol{x}_{i}\right)-1+\xi_{i} \geq 0 \\ \alpha_{i}\left(y_{i} f\left(\boldsymbol{x}_{i}\right)-1+\xi_{i}\right)=0 \\ \xi_{i} \geq 0, \mu_{i} \xi_{i}=0\end{array}\right. $$

约束对应的几种情况, 模型仅与支持向量有关(稀疏性):

$$ \left\{\begin{array}{l} \alpha_{i} = 0, &样本分类正确且对f无影响\\ \alpha_{i}>0, &样本为支持向量,y_{i}f\left(\boldsymbol{x}_{i}\right)=1-\xi_{i}\leq 1 \\ &\left\{\begin{array}{b} \alpha_{i} \lt C , & \mu_i \gt 0,\xi_{i}=0\\ &在间隔边界上\\ \alpha_{i}=C,&\mu_i=0 \\ &\left\{\begin{array}{cc} \xi_{i}\leq 1,&y_{i}f\left(\boldsymbol{x}_{i}\right)\geq 0\\ &间隔边界内部\\ \xi_{i}>1,&y_{i}f\left(\boldsymbol{x}_{i}\right)<0\\ &分类错误\\ \end{array}\right. \\ \end{array}\right. \\ \end{array}\right.  $$

正则化

模型性质与替代损失函数直接相关, 替代损失函数效果:

hinge损失函数, 软间隔支持向量机. 仍保持稀疏性.

对率损失函数，得近似对率回归模型. 但输出失去概率意义, 不能直接用于多分类任务.

正则化 (regularization) 问题一般形式:

$$ \min _{f} \Omega (f)+C \sum_{i=1}^{m} \ell (f(\boldsymbol{x}_i),y_i) $$

正则化项/结构风险(structural risk): 描述间隔大小, 模型f性质, 削减假设空间, 降低过拟合风险. 常用L_2范数(norm) 分量取值均衡, 即非零分量个数稠密. L_1, L_0分量稀疏, 非零分量个数少.

$$ \Omega (f)=\left\{ \begin{array}{1} \|w\|_0,\|w\|_1&稀疏\\ \|w\|_2&稠密 \end{array} \right. $$

经验风险(empirical risk): 描述训练集误差.

$$ \sum_{i=1}^{m} \ell (f(\boldsymbol{x}_i),y_i) $$

正则化常数: C对二者折中.

6.5 支持向量回归

传统回归损失: 模型f(x)与真实y差别, 当完全相同，损失为零.

支持向量回归SVR (Support Vector Regression): 容忍f(x)与y偏差ϵ，当f(x)与y差别绝对值大于ϵ 计算损失. 即以f(x)为中心构建宽度为2ϵ的间隔带，训练样本落入间隔带认为预测正确.

SVR 问题优化目标:

$$ \begin{aligned} \min _{\boldsymbol{w}, b, \xi_{i}} & \frac{1}{2}\|\boldsymbol{w}\|^{2}+C \sum_{i=1}^{m} \ell_{\epsilon}(f(\boldsymbol{x}_{i})-y_i)  \end{aligned} $$

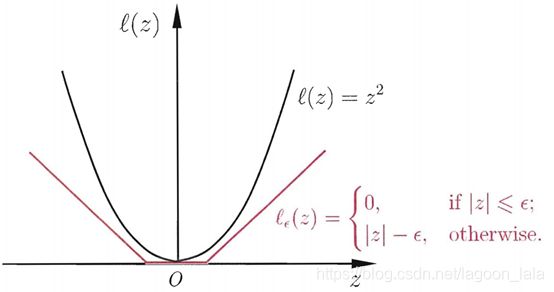
其中C为正则化常数，l_ϵ为不敏感损失 (ϵ-insensitive loss)函数:

$$ \ell_{\epsilon} (z)=\left\{\begin{array}{l} 0,& if~|z|\leq\epsilon;\\|z|-\epsilon,& otherwise. \end{array}\right.  $$

l_ϵ对比传统损失函数:

代入间隔带两侧的松弛变量ξ与ξ hat, 用松弛变量及其约束表示损失函数:

$$ \begin{aligned} \min _{\boldsymbol{w}, b, \xi_{i},\hat\xi_{i}} & \frac{1}{2}\|\boldsymbol{w}\|^{2}+C \sum_{i=1}^{m} (\xi_{i}+\hat\xi_{i}) \\ \text { s.t. } & f(\boldsymbol{x}_{i})-y_{i}\leq \epsilon+\xi_{i}, \\ & y_{i}-f(\boldsymbol{x}_{i})\leq \epsilon+\hat\xi_{i}, \\ & \xi_{i} \geq 0,\hat\xi_{i} \geq 0, i=1,2, \ldots, m \end{aligned} $$

其中的约束条件就是不敏感损失函数的表达, 不理解的时候可以参照着看. 如f-y>0时代表预测值在真实值上方:

$$ f(\boldsymbol{x}_{i})-y_{i}-\epsilon=\xi_{i}>0\\ y_{i}-f(\boldsymbol{x}_{i})-\epsilon< 0, \xi_{i}=0 $$

类似软间隔SVM, 引入拉格朗日乘子μ, μ hat, α, α hat≥0, 得拉格朗日函数:

$$ L(\boldsymbol{w},b,\boldsymbol{\alpha},\boldsymbol{\hat\alpha},\boldsymbol{\xi},\boldsymbol{\hat\xi},\boldsymbol{\mu},\boldsymbol{\hat\mu}) =\frac{1}{2}||\boldsymbol{w}||^2+C\sum_{i=1}^m (\xi_i+\hat\xi_i)+\sum_{i=1}^m \alpha_i(f(\boldsymbol{x}_i)-y_i-\epsilon-\xi_i)+\sum_{i=1}^m \hat\alpha_i(y_i-f(\boldsymbol{x}_i)-\epsilon-\hat\xi_i)-\sum_{i=1}^m\mu_i \xi_i-\sum_{i=1}^m\hat\mu_i \hat\xi_i $$

其中后四项, 为优化目标中的约束转化为小于等于0的形式. 如对于约束ξ≥0则取-ξ≤0.

代入划分超平面模型:

$$ f(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+b $$

L对w, b, ξ, ξ hat求偏导为0得:

$$ \boldsymbol{w}=\sum_{i=1}^{m}(\hat\alpha_{i}-\alpha_{i})\boldsymbol{x}_{i}\\ 0=\sum_{i=1}^{m}(\hat\alpha_{i}-\alpha_{i})\\ C=\alpha_i +\mu_i\\ C=\hat\alpha_i +\hat\mu_i $$

L中的(α+μ), (α hat- α), f,w分别整理代入, 其中注意:

$$ \begin{aligned} &f(\boldsymbol{x}_i)=\boldsymbol{w}^T\boldsymbol{x_i}+b\\ \Rightarrow &\sum_{i=1}^m \alpha_if(\boldsymbol{x}_i)-\sum_{i=1}^m \hat\alpha_if(\boldsymbol{x}_i)\\ &=\sum_{i=1}^m (\alpha_i-\hat\alpha_i)(\boldsymbol{w}^T\boldsymbol{x_i}+b)\\ &=\sum_{i=1}^m (\alpha_i-\hat\alpha_i)(\boldsymbol{w}^T\boldsymbol{x_i})+\sum_{i=1}^m (\alpha_i-\hat\alpha_i)b\\ &=-\boldsymbol{w}^T\sum_{i=1}^m (\hat\alpha_i-\alpha_i)\boldsymbol{x_i}-b\sum_{i=1}^m (\hat\alpha_i-\alpha_i)\\ &=-\boldsymbol{w}^T\boldsymbol{w}-0\\ &\frac{1}{2}\|\boldsymbol{w}\|^2=\frac{1}{2}\boldsymbol{w}^T\boldsymbol{w}\\ &=\frac{1}{2}(\sum_{i=1}^{m}(\hat\alpha_{i}-\alpha_{i})\boldsymbol{x}_{i})^T(\sum_{i=1}^{m}(\hat\alpha_{i}-\alpha_{i})\boldsymbol{x}_{i})\\  &=\frac {1}{2}\sum_{i=1 }^{m}\sum_{j=1}^{m}(\hat\alpha_i-\alpha_i)(\hat\alpha_j-\alpha_j)\boldsymbol{x}_i^T\boldsymbol{x}_j \end{aligned} $$

得SVR对偶问题:

$$ \begin{aligned} \max_{\boldsymbol{\alpha},\boldsymbol{\hat\alpha}}&\sum _{i=1}^m y_i(\hat\alpha_i-\alpha_i)-\epsilon(\hat\alpha_i+\alpha_i)-\frac {1}{2}\sum_{i=1 }^{m}\sum_{j=1}^{m}(\hat\alpha_i-\alpha_i)(\hat\alpha_j-\alpha_j)\boldsymbol{x}_i^T\boldsymbol{x}_j \\ s.t. &\sum_{i=1}^m \hat\alpha_i-\alpha_i=0 \\ & 0 \leq\alpha_i,\hat\alpha_i \leq C \quad i=1,2,\dots ,m \end{aligned} $$

其中约束皆可由偏导为0的几个式子导出:

$$ \left\{\begin{array} {c} C=\hat\alpha_i +\hat\mu_i\\ \hat\mu_i\geq 0 \end{array}\right. \\ \Longrightarrow\hat\alpha_i \leq C  $$

KKT条件:

$$ \left\{\begin{array}{l} {\alpha_{i}\left(f\left(\boldsymbol{x}_{i}\right)-y_{i}-\epsilon-\xi_{i}\right)=0} \\ {\hat{\alpha}_{i}\left(y_{i}-f\left(\boldsymbol{x}_{i}\right)-\epsilon-\hat{\xi}_{i}\right)=0} \\ {\alpha_{i} \hat{\alpha}_{i}=0, \xi_{i} \hat{\xi}_{i}=0} \\ {\left(C-\alpha_{i}\right) \xi_{i}=0,\left(C-\hat{\alpha}_{i}\right) \hat{\xi}_{i}=0} \end{array}\right. $$

样本只可能处在间隔带的某一侧，根据不敏感损失函数, 两者至少有一个不成立:

$$ f(\boldsymbol{x}_{i})-y_{i}-\epsilon=\xi_{i}>0\\ \Rightarrow f(\boldsymbol{x}_{i})-y_{i}-\epsilon-\xi_{i}=0\\ y_{i}-f(\boldsymbol{x}_{i})-\epsilon< 0, \xi_{i}=0\\ \Rightarrow y_{i}-f(\boldsymbol{x}_{i})-\epsilon-\xi_{i}\neq 0 $$

所以α与α hat中至少有一个为0，ξi, hat ξ​i​中也是至少有一个为0. 只有样本落在间隔带外, α与α hat其中的一个能取非0值. 间隔带内则两个值都为0.

SVR的解:

$$ f(x)=\sum_{i=1}^m(\hat\alpha_i-\alpha_i)\boldsymbol{x}_i^T\boldsymbol{x}+b $$

其中α与α hat中至少有一个为0. 若同时为0, 在间隔带内则非支持向量.

而SVR的支持向量落在间隔带外, 满足:

$$ \hat\alpha_i-\alpha_i\neq 0  $$

SVR解仍具有稀疏性.

求解b:

$$ b=y_i-\epsilon-\sum_{i=1}^m(\hat\alpha_i-\alpha_i)\boldsymbol{x}^T_i\boldsymbol{x} $$

一般为了防止误差取多个样本代入所解的平均值.

推导b公式:

$$ f(\boldsymbol{x}_i)-y_i-\epsilon-\xi_i=0 $$

代入:

$$ f(\boldsymbol{x}_i)=\sum_{i=1}^m(\hat\alpha_i-\alpha_i)\boldsymbol{x}^T_i\boldsymbol{x}+b,\\ \xi_i=0 $$

若考虑特征映射, w的解形式为(未考虑则与偏导为0所求式子同):

$$ \boldsymbol{w}=\sum_{i=1}^{m}(\hat\alpha_{i}-\alpha_{i})\phi(\boldsymbol{x}_{i}) $$

代入特征映射后SVR的划分超平面:

$$ f(\boldsymbol{x})=\sum_{i=1}^m(\hat\alpha_i-\alpha_i)\kappa (\boldsymbol{x},\boldsymbol{x}_i)+b $$

6.6 核方法

表示定理: 令H为核函数κ对应的再生核希尔伯特空间, 关于h的范数||h||，对单调递增函数Ω和非负损失函数l. 优化问题:

$$ \min _{h\in\mathbb H}F(h)= \Omega (\|h\|_{\mathbb H})+\ell (h(\boldsymbol{x}_1),\cdots,h(\boldsymbol{x}_m)) $$

其最优解可写作核函数的线性组合:

$$ h^*(\boldsymbol{x})=\sum_{i=1}^{m} \alpha_{i} \kappa\left(\boldsymbol{x}, \boldsymbol{x}_{i}\right) $$

其中α是核函数κ线性组合的系数

核方法 (kernel methods): 基于核函数的学习方法. 核化引入核函数, 将线性学习器拓展为非线性学习器.

核线性判别分析KLDA (Kernelized Linear Discriminant Analysis)学习目标:

$$ \max _{\boldsymbol{w}} J(\boldsymbol{w})=\frac{\boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{b}^{\phi} \boldsymbol{w}}{\boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{w}^{\phi} \boldsymbol{w}} $$

学习目标J类似线性判别分析LDA的最大化目标: 广义瑞利商.

$$ J= \frac{\boldsymbol w^{\mathrm{T}}\boldsymbol{\mathrm S}_b\boldsymbol w}{\boldsymbol w^{\mathrm{T}}\boldsymbol{\mathrm S}_w\boldsymbol w} $$

解形式(直线方程的固定形式):

$$ h(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}}\phi(\boldsymbol{x}) $$

其中:

$$ \boldsymbol{w}=\sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right) $$

用核函数表达映射Φ则为投影函数(投影直线方程):

$$ h(\boldsymbol{x})=\sum_{i=1}^{m} \alpha_{i} \kappa\left(\boldsymbol{x}, \boldsymbol{x}_{i}\right) $$

可以看出, 模型核化往往将x的映射用核函数k来表示, 在矩阵形式中, 也就是核矩阵K.

这也就是核化后的输入没有再出现x的原因: 核技巧不计算x到高维空间的映射, 而是直接计算两个映射的内积.

推导w投影后形式: 将直线方程的固定形式h(x)代入投影形式h(x)有 $$ \begin{aligned} h(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}}\phi(\boldsymbol{x})&=\sum_{i=1}^{m} \alpha_{i} \kappa\left(\boldsymbol{x}, \boldsymbol{x}_{i}\right)\\ &=\sum_{i=1}^{m} \alpha_{i} \phi(\boldsymbol{x})^{\mathrm{T}}\phi(\boldsymbol{x}_i)\\ &=\phi(\boldsymbol{x})^{\mathrm{T}}\cdot\sum_{i=1}^{m} \alpha_{i} \phi(\boldsymbol{x}_i) \end{aligned} $$ 注意其计算结果h(x)为标量, 其转置等于本身 $$ \begin{aligned} \boldsymbol{w}^{\mathrm{T}}\phi(\boldsymbol{x})=\phi(\boldsymbol{x})^{\mathrm{T}}\boldsymbol{w}&=\phi(\boldsymbol{x})^{\mathrm{T}}\cdot\sum_{i=1}^{m} \alpha_{i} \phi(\boldsymbol{x}_i)\\ \Rightarrow\boldsymbol{w}&=\sum_{i=1}^{m} \alpha_{i} \phi(\boldsymbol{x}_i) \end{aligned} $$

类间散度矩阵:

$$ \mathbf{S}_{b}^{\phi}=\left(\boldsymbol{\mu}_{1}^{\phi}-\boldsymbol{\mu}_{0}^{\phi}\right)\left(\boldsymbol{\mu}_{1}^{\phi}-\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}} $$

类内散度矩阵:

$$ \mathbf{S}_{w}^{\phi}=\sum_{i=0}^{1} \sum_{\boldsymbol{x} \in X_{i}}\left(\phi(\boldsymbol{x})-\boldsymbol{\mu}_{i}^{\phi}\right)\left(\phi(\boldsymbol{x})-\boldsymbol{\mu}_{i}^{\phi}\right)^{\mathrm{T}} $$

其中, X_i表示第i类样本集合, 样本数m_i. 总样本数m=m0+m1. 第i类样本均值:

$$ {\boldsymbol{\mu}}_{i}^{\phi}=\frac{1}{m_{i}} \sum_{\boldsymbol{x} \in X_{i}}\phi(\boldsymbol{x}) $$

K为核函数κ对应的核矩阵:

$$ {\textbf K}_{ij}=\kappa(\boldsymbol{x}_i,\boldsymbol{x}_j) $$

第i类样本的指示向量:

$$ \mathbf{1}_{i}\in\{1,0\}^{m\times 1}\\ \mathbf{1}_{ij}= \left\{\begin{array}{c} 1,&if~\boldsymbol{x}_j\in X_i\\ 0,&if~\boldsymbol{x}_j\notin X_i\\ \end{array}\right.  $$

定义变量:

$$ \hat{\boldsymbol{\mu}}_{0}=\frac{1}{m_{0}} \mathbf{K} \mathbf{1}_{0}\\ \hat{\boldsymbol{\mu}}_{1}=\frac{1}{m_{1}} \mathbf{K} \mathbf{1}_{1} $$

公式使用例子:

假设有4个样本，第1第3个样本标记为0，第2第4个样本的标记为1.

$$ m=4,m_0=2,m_1=2;\\ X_0=\{\boldsymbol{x}_1,\boldsymbol{x}_3\},X_1=\{\boldsymbol{x}_2,\boldsymbol{x}_4\}\\ \mathbf{K}=\left[ \begin{array}{cccc} \kappa\left(\boldsymbol{x}_1, \boldsymbol{x}_1\right) & \kappa\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right) & \kappa\left(\boldsymbol{x}_1, \boldsymbol{x}_3\right) & \kappa\left(\boldsymbol{x}_1, \boldsymbol{x}_4\right)\\ \kappa\left(\boldsymbol{x}_2, \boldsymbol{x}_1\right) & \kappa\left(\boldsymbol{x}_2, \boldsymbol{x}_2\right) & \kappa\left(\boldsymbol{x}_2, \boldsymbol{x}_3\right) & \kappa\left(\boldsymbol{x}_2, \boldsymbol{x}_4\right)\\ \kappa\left(\boldsymbol{x}_3, \boldsymbol{x}_1\right) & \kappa\left(\boldsymbol{x}_3, \boldsymbol{x}_2\right) & \kappa\left(\boldsymbol{x}_3, \boldsymbol{x}_3\right) & \kappa\left(\boldsymbol{x}_3, \boldsymbol{x}_4\right)\\ \kappa\left(\boldsymbol{x}_4, \boldsymbol{x}_1\right) & \kappa\left(\boldsymbol{x}_4, \boldsymbol{x}_2\right) & \kappa\left(\boldsymbol{x}_4, \boldsymbol{x}_3\right) & \kappa\left(\boldsymbol{x}_4, \boldsymbol{x}_4\right)\\ \end{array} \right]\in \mathbb{R}^{4\times 4}\\ \mathbf{1}_{0}=\left[ \begin{array}{c} 1\\ 0\\ 1\\ 0\\ \end{array} \right]\in \mathbb{R}^{4\times 1}, \mathbf{1}_{1}=\left[ \begin{array}{c} 0\\ 1\\ 0\\ 1\\ \end{array} \right]\in \mathbb{R}^{4\times 1}\\ \hat{\boldsymbol{\mu}}_{0}=\frac{1}{m_{0}} \mathbf{K} \mathbf{1}_{0}=\frac{1}{2}\left[ \begin{array}{c} \kappa\left(\boldsymbol{x}_1, \boldsymbol{x}_1\right)+\kappa\left(\boldsymbol{x}_1, \boldsymbol{x}_3\right)\\ \kappa\left(\boldsymbol{x}_2, \boldsymbol{x}_1\right)+\kappa\left(\boldsymbol{x}_2, \boldsymbol{x}_3\right)\\ \kappa\left(\boldsymbol{x}_3, \boldsymbol{x}_1\right)+\kappa\left(\boldsymbol{x}_3, \boldsymbol{x}_3\right)\\ \kappa\left(\boldsymbol{x}_4, \boldsymbol{x}_1\right)+\kappa\left(\boldsymbol{x}_4, \boldsymbol{x}_3\right)\\ \end{array} \right]\in \mathbb{R}^{4\times 1}\\ \hat{\boldsymbol{\mu}}_{1}=\frac{1}{m_{1}} \mathbf{K} \mathbf{1}_{1}=\frac{1}{2}\left[ \begin{array}{c} \kappa\left(\boldsymbol{x}_1, \boldsymbol{x}_2\right)+\kappa\left(\boldsymbol{x}_1, \boldsymbol{x}_4\right)\\ \kappa\left(\boldsymbol{x}_2, \boldsymbol{x}_2\right)+\kappa\left(\boldsymbol{x}_2, \boldsymbol{x}_4\right)\\ \kappa\left(\boldsymbol{x}_3, \boldsymbol{x}_2\right)+\kappa\left(\boldsymbol{x}_3, \boldsymbol{x}_4\right)\\ \kappa\left(\boldsymbol{x}_4, \boldsymbol{x}_2\right)+\kappa\left(\boldsymbol{x}_4, \boldsymbol{x}_4\right)\\ \end{array} \right]\in \mathbb{R}^{4\times 1} $$

hat μ的一般形式:

$$ \hat{\boldsymbol{\mu}}_{0}=\frac{1}{m_{0}} \mathbf{K} \mathbf{1}_{0}=\frac{1}{m_{0}}\left[ \begin{array}{c} \sum_{\boldsymbol{x} \in X_{0}}\kappa\left(\boldsymbol{x}_1, \boldsymbol{x}\right)\\ \sum_{\boldsymbol{x} \in X_{0}}\kappa\left(\boldsymbol{x}_2, \boldsymbol{x}\right)\\ \vdots\\ \sum_{\boldsymbol{x} \in X_{0}}\kappa\left(\boldsymbol{x}_m, \boldsymbol{x}\right)\\ \end{array} \right]\in \mathbb{R}^{m\times 1}\\ \hat{\boldsymbol{\mu}}_{1}=\frac{1}{m_{1}} \mathbf{K} \mathbf{1}_{1}=\frac{1}{m_{1}}\left[ \begin{array}{c} \sum_{\boldsymbol{x} \in X_{1}}\kappa\left(\boldsymbol{x}_1, \boldsymbol{x}\right)\\ \sum_{\boldsymbol{x} \in X_{1}}\kappa\left(\boldsymbol{x}_2, \boldsymbol{x}\right)\\ \vdots\\ \sum_{\boldsymbol{x} \in X_{1}}\kappa\left(\boldsymbol{x}_m, \boldsymbol{x}\right)\\ \end{array} \right]\in \mathbb{R}^{m\times 1} $$

定义:

$$ \mathbf{M}=\left(\boldsymbol{\hat\mu}_{0}-\boldsymbol{\hat\mu}_{1}\right)\left(\boldsymbol{\hat\mu}_{0}-\boldsymbol{\hat\mu}_{1}\right)^{\mathrm{T}} \\ \mathbf{N}=\mathbf{K} \mathbf{K}^{\mathrm{T}}-\sum_{i=0}^{1} m_{i} \hat{\boldsymbol{\mu}}_{i} \hat{\boldsymbol{\mu}}_{i}^{\mathrm{T}} $$

KLDA学习目标可化为:

$$ \max _{\boldsymbol{\alpha}} J(\boldsymbol{\alpha})=\frac{\boldsymbol{\alpha}^{\mathrm{T}} \mathbf{M} \boldsymbol{\alpha}}{\boldsymbol{\alpha}^{\mathrm{T}} \mathbf{N} \boldsymbol{\alpha}} $$

上式推导分子部分(即代入几个定义的变量):

将w投影后形式代入J的分子

$$ \begin{aligned} \boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{b}^{\phi} \boldsymbol{w}&=\left(\sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)\right)^{\mathrm{T}}\cdot\mathbf{S}_{b}^{\phi}\cdot \sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right) \\ &=\sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}\cdot\mathbf{S}_{b}^{\phi}\cdot \sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right) \\ \end{aligned} $$

其中S_b根据公式, 其中为μ^Φ而非hat μ不要代错了公式:

\begin{aligned} \mathbf{S}_{b}^{\phi} &=\left(\boldsymbol{\mu}_{1}^{\phi}-\boldsymbol{\mu}_{0}^{\phi}\right)\left(\boldsymbol{\mu}_{1}^{\phi}-\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}} \\ &=\left(\frac{1}{m_{1}} \sum_{\boldsymbol{x} \in X_{1}} \phi(\boldsymbol{x})-\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \phi(\boldsymbol{x})\right)\left(\frac{1}{m_{1}} \sum_{\boldsymbol{x} \in X_{1}} \phi(\boldsymbol{x})-\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \phi(\boldsymbol{x})\right)^{\mathrm{T}} \\ &=\left(\frac{1}{m_{1}} \sum_{\boldsymbol{x} \in X_{1}} \phi(\boldsymbol{x})-\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \phi(\boldsymbol{x})\right)\left(\frac{1}{m_{1}} \sum_{\boldsymbol{x} \in X_{1}} \phi(\boldsymbol{x})^{\mathrm{T}}-\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \phi(\boldsymbol{x})^{\mathrm{T}}\right) \\ \end{aligned}

将S_b代入分子:

$$ \begin{aligned} \boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{b}^{\phi} \boldsymbol{w}=&\sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}\cdot\left(\frac{1}{m_{1}} \sum_{\boldsymbol{x} \in X_{1}} \phi(\boldsymbol{x})-\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \phi(\boldsymbol{x})\right)\cdot\left(\frac{1}{m_{1}} \sum_{\boldsymbol{x} \in X_{1}} \phi(\boldsymbol{x})^{\mathrm{T}}-\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \phi(\boldsymbol{x})^{\mathrm{T}}\right)\cdot \sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right) \\ =&\left(\frac{1}{m_{1}} \sum_{\boldsymbol{x} \in X_{1}}\sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}} \phi(\boldsymbol{x})-\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}\phi(\boldsymbol{x})\right)\\ &\cdot\left(\frac{1}{m_{1}} \sum_{\boldsymbol{x} \in X_{1}} \sum_{i=1}^{m} \alpha_{i} \phi(\boldsymbol{x})^{\mathrm{T}}\phi\left(\boldsymbol{x}_{i}\right)-\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \sum_{i=1}^{m} \alpha_{i} \phi(\boldsymbol{x})^{\mathrm{T}}\phi\left(\boldsymbol{x}_{i}\right)\right) \\ \end{aligned} $$

由于κ为标量, 标量转置不变:

$$ \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}\right)=\phi(\boldsymbol{x}_i)^{\mathrm{T}}\phi(\boldsymbol{x})=\left(\phi(\boldsymbol{x}_i)^{\mathrm{T}}\phi(\boldsymbol{x})\right)^{\mathrm{T}}=\phi(\boldsymbol{x})^{\mathrm{T}}\phi(\boldsymbol{x}_i)=\kappa\left(\boldsymbol{x}_i, \boldsymbol{x}\right)^{\mathrm{T}} $$

代入κ即为:

$$ \begin{aligned} \boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{b}^{\phi} \boldsymbol{w}=&\left(\frac{1}{m_{1}} \sum_{i=1}^{m}\sum_{\boldsymbol{x} \in X_{1}}\alpha_{i} \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}\right)-\frac{1}{m_{0}} \sum_{i=1}^{m} \sum_{\boldsymbol{x} \in X_{0}} \alpha_{i} \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}\right)\right)\\ &\cdot\left(\frac{1}{m_{1}} \sum_{i=1}^{m}\sum_{\boldsymbol{x} \in X_{1}} \alpha_{i} \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}\right)-\frac{1}{m_{0}}\sum_{i=1}^{m} \sum_{\boldsymbol{x} \in X_{0}} \alpha_{i} \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}\right)\right) \end{aligned} $$

再代入hat μ的一般形式(即hat μ代入K与指示函数展开后的形式):

$$ \begin{aligned} \boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{b}^{\phi} \boldsymbol{w}&=\left(\boldsymbol{\alpha}^{\mathrm{T}}\hat{\boldsymbol{\mu}}_{1}-\boldsymbol{\alpha}^{\mathrm{T}}\hat{\boldsymbol{\mu}}_{0}\right)\cdot\left(\hat{\boldsymbol{\mu}}_{1}^{\mathrm{T}}\boldsymbol{\alpha}-\hat{\boldsymbol{\mu}}_{0}^{\mathrm{T}}\boldsymbol{\alpha}\right)\\ &=\boldsymbol{\alpha}^{\mathrm{T}}\cdot\left(\hat{\boldsymbol{\mu}}_{1}-\hat{\boldsymbol{\mu}}_{0}\right)\cdot\left(\hat{\boldsymbol{\mu}}_{1}^{\mathrm{T}}-\hat{\boldsymbol{\mu}}_{0}^{\mathrm{T}}\right)\cdot\boldsymbol{\alpha}\\ &=\boldsymbol{\alpha}^{\mathrm{T}}\cdot\left(\hat{\boldsymbol{\mu}}_{1}-\hat{\boldsymbol{\mu}}_{0}\right)\cdot\left(\hat{\boldsymbol{\mu}}_{1}-\hat{\boldsymbol{\mu}}_{0}\right)^{\mathrm{T}}\cdot\boldsymbol{\alpha}\\ &=\boldsymbol{\alpha}^{\mathrm{T}} \mathbf{M} \boldsymbol{\alpha}\\ \end{aligned} $$

推导分母部分

w代入J:

$$ \begin{aligned} \boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{w}^{\phi} \boldsymbol{w}&=\left(\sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)\right)^{\mathrm{T}}\cdot\mathbf{S}_{w}^{\phi}\cdot \sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right) \\ &=\sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}\cdot\mathbf{S}_{w}^{\phi}\cdot \sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right) \\ \end{aligned} $$

其中S_w:

$$ \begin{aligned} \mathbf{S}_{w}^{\phi}&=\sum_{i=0}^{1} \sum_{\boldsymbol{x} \in X_{i}}\left(\phi(\boldsymbol{x})-\boldsymbol{\mu}_{i}^{\phi}\right)\left(\phi(\boldsymbol{x})-\boldsymbol{\mu}_{i}^{\phi}\right)^{\mathrm{T}} \\ &=\sum_{i=0}^{1} \sum_{\boldsymbol{x} \in X_{i}}\left(\phi(\boldsymbol{x})-\boldsymbol{\mu}_{i}^{\phi}\right)\left(\phi(\boldsymbol{x})^{\mathrm{T}}-\left(\boldsymbol{\mu}_{i}^{\phi}\right)^{\mathrm{T}}\right) \\ &=\sum_{i=0}^{1} \sum_{\boldsymbol{x} \in X_{i}}\left(\phi(\boldsymbol{x})\phi(\boldsymbol{x})^{\mathrm{T}}-\phi(\boldsymbol{x})\left(\boldsymbol{\mu}_{i}^{\phi}\right)^{\mathrm{T}}-\boldsymbol{\mu}_{i}^{\phi}\phi(\boldsymbol{x})^{\mathrm{T}}+\boldsymbol{\mu}_{i}^{\phi}\left(\boldsymbol{\mu}_{i}^{\phi}\right)^{\mathrm{T}}\right) \\ &=\sum_{i=0}^{1} \sum_{\boldsymbol{x} \in X_{i}}\phi(\boldsymbol{x})\phi(\boldsymbol{x})^{\mathrm{T}}-\sum_{i=0}^{1} \sum_{\boldsymbol{x} \in X_{i}}\phi(\boldsymbol{x})\left(\boldsymbol{\mu}_{i}^{\phi}\right)^{\mathrm{T}}-\sum_{i=0}^{1} \sum_{\boldsymbol{x} \in X_{i}}\boldsymbol{\mu}_{i}^{\phi}\phi(\boldsymbol{x})^{\mathrm{T}}+\sum_{i=0}^{1} \sum_{\boldsymbol{x} \in X_{i}}\boldsymbol{\mu}_{i}^{\phi}\left(\boldsymbol{\mu}_{i}^{\phi}\right)^{\mathrm{T}} \\ \end{aligned} $$

其中后三项分别可代入μ^Φ化简:

$$ \begin{aligned} \sum_{i=0}^{1} \sum_{\boldsymbol{x} \in X_{i}} \phi(\boldsymbol{x})\left(\boldsymbol{\mu}_{i}^{\phi}\right)^{\mathrm{T}} &=\sum_{\boldsymbol{x} \in X_{0}} \phi(\boldsymbol{x})\left(\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}}+\sum_{\boldsymbol{x} \in X_{1}} \phi(\boldsymbol{x})\left(\boldsymbol{\mu}_{1}^{\phi}\right)^{\mathrm{T}} \\ &=m_{0} \boldsymbol{\mu}_{0}^{\phi}\left(\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}}+m_{1} \boldsymbol{\mu}_{1}^{\phi}\left(\boldsymbol{\mu}_{1}^{\phi}\right)^{\mathrm{T}} \\ \sum_{i=0}^{1} \sum_{\boldsymbol{x} \in X_{i}} \boldsymbol{\mu}_{i}^{\phi} \phi(\boldsymbol{x})^{\mathrm{T}} &=\sum_{i=0}^{1} \boldsymbol{\mu}_{i}^{\phi} \sum_{\boldsymbol{x} \in X_{i}} \phi(\boldsymbol{x})^{\mathrm{T}} \\ &=\boldsymbol{\mu}_{0}^{\phi} \sum_{\boldsymbol{x} \in X_{0}} \phi(\boldsymbol{x})^{\mathrm{T}}+\boldsymbol{\mu}_{1}^{\phi} \sum_{\boldsymbol{x} \in X_{1}} \phi(\boldsymbol{x})^{\mathrm{T}} \\ &=m_{0} \boldsymbol{\mu}_{0}^{\phi}\left(\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}}+m_{1} \boldsymbol{\mu}_{1}^{\phi}\left(\boldsymbol{\mu}_{1}^{\phi}\right)^{\mathrm{T}}\\ \sum_{i=0}^{1} \sum_{\boldsymbol{x} \in X_{i}}\boldsymbol{\mu}_{i}^{\phi}\left(\boldsymbol{\mu}_{i}^{\phi}\right)^{\mathrm{T}}&=\sum_{\boldsymbol{x} \in X_{0}}\boldsymbol{\mu}_{0}^{\phi}\left(\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}}+\sum_{\boldsymbol{x} \in X_{1}}\boldsymbol{\mu}_{1}^{\phi}\left(\boldsymbol{\mu}_{1}^{\phi}\right)^{\mathrm{T}}\\ &=m_0\boldsymbol{\mu}_{0}^{\phi}\left(\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}}+m_1\boldsymbol{\mu}_{1}^{\phi}\left(\boldsymbol{\mu}_{1}^{\phi}\right)^{\mathrm{T}} \end{aligned} $$

代入S_w得:

$$ \begin{aligned} \mathbf{S}_{w}^{\phi}&=\sum_{\boldsymbol{x} \in D}\phi(\boldsymbol{x})\phi(\boldsymbol{x})^{\mathrm{T}}-2\left[m_0\boldsymbol{\mu}_{0}^{\phi}\left(\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}}+m_1\boldsymbol{\mu}_{1}^{\phi}\left(\boldsymbol{\mu}_{1}^{\phi}\right)^{\mathrm{T}}\right]+m_0 \boldsymbol{\mu}_{0}^{\phi}\left(\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}}+m_1 \boldsymbol{\mu}_{1}^{\phi}\left(\boldsymbol{\mu}_{1}^{\phi}\right)^{\mathrm{T}} \\ &=\sum_{\boldsymbol{x} \in D}\phi(\boldsymbol{x})\phi(\boldsymbol{x})^{\mathrm{T}}-m_0\boldsymbol{\mu}_{0}^{\phi}\left(\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}}-m_1\boldsymbol{\mu}_{1}^{\phi}\left(\boldsymbol{\mu}_{1}^{\phi}\right)^{\mathrm{T}}\\ \end{aligned} $$

S_w代回分母为:

$$ \begin{aligned} \boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{w}^{\phi} \boldsymbol{w}=&\sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}\cdot\mathbf{S}_{w}^{\phi}\cdot \sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right) \\ =&\sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}\cdot\left(\sum_{\boldsymbol{x} \in D}\phi(\boldsymbol{x})\phi(\boldsymbol{x})^{\mathrm{T}}-m_0\boldsymbol{\mu}_{0}^{\phi}\left(\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}}-m_1\boldsymbol{\mu}_{1}^{\phi}\left(\boldsymbol{\mu}_{1}^{\phi}\right)^{\mathrm{T}}\right)\cdot \sum_{i=1}^{m} \alpha_{i} \phi\left(\boldsymbol{x}_{i}\right) \\ =&\sum_{i=1}^{m}\sum_{j=1}^{m}\sum_{\boldsymbol{x} \in D}\alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}\phi(\boldsymbol{x})\phi(\boldsymbol{x})^{\mathrm{T}}\alpha_{j} \phi\left(\boldsymbol{x}_{j}\right)-\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}m_0\boldsymbol{\mu}_{0}^{\phi}\left(\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}}\alpha_{j} \phi\left(\boldsymbol{x}_{j}\right)\\ &-\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}m_1\boldsymbol{\mu}_{1}^{\phi}\left(\boldsymbol{\mu}_{1}^{\phi}\right)^{\mathrm{T}}\alpha_{j} \phi\left(\boldsymbol{x}_{j}\right) \\ \end{aligned} $$

其中三项分别代入K, hat μ, 可化为

$$ \begin{aligned} \sum_{i=1}^{m}\sum_{j=1}^{m}\sum_{\boldsymbol{x} \in D}\alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}\phi(\boldsymbol{x})\phi(\boldsymbol{x})^{\mathrm{T}}\alpha_{j} \phi\left(\boldsymbol{x}_{j}\right)&=\sum_{i=1}^{m}\sum_{j=1}^{m}\sum_{\boldsymbol{x} \in D}\alpha_{i} \alpha_{j}\kappa\left(\boldsymbol{x}_i, \boldsymbol{x}\right)\kappa\left(\boldsymbol{x}_j, \boldsymbol{x}\right)\\ &=\boldsymbol{\alpha}^{\mathrm{T}} \mathbf{K} \mathbf{K}^{\mathrm{T}} \boldsymbol{\alpha} \\ \sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}m_0\boldsymbol{\mu}_{0}^{\phi}\left(\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}}\alpha_{j} \phi\left(\boldsymbol{x}_{j}\right)&=m_0\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}\phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}\boldsymbol{\mu}_{0}^{\phi}\left(\boldsymbol{\mu}_{0}^{\phi}\right)^{\mathrm{T}} \phi\left(\boldsymbol{x}_{j}\right)\\ &=m_0\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}\phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}\left[\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \phi(\boldsymbol{x})\right]\left[\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \phi(\boldsymbol{x})\right]^{\mathrm{T}} \phi\left(\boldsymbol{x}_{j}\right)\\ &=m_0\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}\left[\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}\phi(\boldsymbol{x})\right]\left[\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \phi(\boldsymbol{x})^{\mathrm{T}}\phi\left(\boldsymbol{x}_{j}\right)\right] \\ &=m_0\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i}\alpha_{j}\left[\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \kappa\left(\boldsymbol{x}_i, \boldsymbol{x}\right)\right]\left[\frac{1}{m_{0}} \sum_{\boldsymbol{x} \in X_{0}} \kappa\left(\boldsymbol{x}_j, \boldsymbol{x}\right)\right] \\ &=m_0\boldsymbol{\alpha}^{\mathrm{T}} \hat{\boldsymbol{\mu}}_{0} \hat{\boldsymbol{\mu}}_{0}^{\mathrm{T}} \boldsymbol{\alpha} \\ \sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_{i} \phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}}m_1\boldsymbol{\mu}_{1}^{\phi}\left(\boldsymbol{\mu}_{1}^{\phi}\right)^{\mathrm{T}}\alpha_{j} \phi\left(\boldsymbol{x}_{j}\right)&=m_1\boldsymbol{\alpha}^{\mathrm{T}} \hat{\boldsymbol{\mu}}_{1} \hat{\boldsymbol{\mu}}_{1}^{\mathrm{T}} \boldsymbol{\alpha} \end{aligned} $$

故分母整理后可代入N:

$$ \begin{aligned} \boldsymbol{w}^{\mathrm{T}} \mathbf{S}_{b}^{\phi} \boldsymbol{w}&=\boldsymbol{\alpha}^{\mathrm{T}} \mathbf{K} \mathbf{K}^{\mathrm{T}} \boldsymbol{\alpha}-m_0\boldsymbol{\alpha}^{\mathrm{T}} \hat{\boldsymbol{\mu}}_{0} \hat{\boldsymbol{\mu}}_{0}^{\mathrm{T}} \boldsymbol{\alpha}-m_1\boldsymbol{\alpha}^{\mathrm{T}} \hat{\boldsymbol{\mu}}_{1} \hat{\boldsymbol{\mu}}_{1}^{\mathrm{T}} \boldsymbol{\alpha}\\ &=\boldsymbol{\alpha}^{\mathrm{T}} \cdot\left(\mathbf{K} \mathbf{K}^{\mathrm{T}} -m_0\hat{\boldsymbol{\mu}}_{0} \hat{\boldsymbol{\mu}}_{0}^{\mathrm{T}} -m_1\hat{\boldsymbol{\mu}}_{1} \hat{\boldsymbol{\mu}}_{1}^{\mathrm{T}} \right)\cdot\boldsymbol{\alpha}\\ &=\boldsymbol{\alpha}^{\mathrm{T}} \cdot\left(\mathbf{K} \mathbf{K}^{\mathrm{T}}-\sum_{i=0}^{1} m_{i} \hat{\boldsymbol{\mu}}_{i} \hat{\boldsymbol{\mu}}_{i}^{\mathrm{T}} \right)\cdot\boldsymbol{\alpha}\\ &=\boldsymbol{\alpha}^{\mathrm{T}} \mathbf{N}\boldsymbol{\alpha}\\ \end{aligned} $$

用线性判别分析求解方法可得α, 代入可得投影函数h.