NLP | Logistic Regression
1.模型数学本质
1.1 描述如下:
三个重要参数:weight bias sigmoid
首先定义: P w , b ( C 1 ∣ x ) ≥ 0.5 Pw,b(C_1| x)\geq0.5 Pw,b(C1∣x)≥0.5则取 C 1 C_1 C1,否则取 C 2 C_2 C2.
逻辑回归的数学表述如下:
f w , b ( x ) = σ ( z ) = 1 1 + e − z , z = ∑ i w i x i + b f_{w,b}(x)=\sigma(z)=\frac{1}{1+e^{-z}}\quad,\quad z=\sum_iw_ix_i+b fw,b(x)=σ(z)=1+e−z1,z=i∑wixi+b
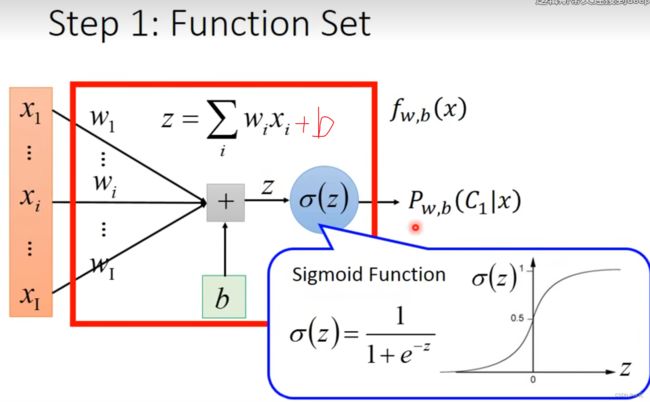
sigmoid function的作用:把输出结果控制在0-1之间。
1.2 求解步骤理解:
1.2.1
先假设训练数据集是由 P w , b ( C 1 ∣ x ) P_{w,b}(C1|x) Pw,b(C1∣x)的分布产生的,则产生这组训练数据的概率为:
L ( w , b ) = f w , b ( x 1 ) f w , b ( x 2 ) ( 1 − f w , b ( x 3 ) ) . . . f w , b ( x n ) L(w,b)=f_{w,b}(x_1)f_{w,b}(x_2)(1-f_{w,b}(x_3))...f_{w,b}(x_n) L(w,b)=fw,b(x1)fw,b(x2)(1−fw,b(x3))...fw,b(xn)
也就是说,我们需要选择合适的 w w w和 b b b,使得产生这组训练数据的可能性最大,即求 L ( w , b ) L(w,b) L(w,b)的最大值。
a r g m a x L ( w , b ) arg~maxL(w,b) arg maxL(w,b)等价于 a r g m i n − l n L ( w , b ) arg~min -lnL(w,b) arg min−lnL(w,b)
− l n L ( w , b ) = l n f w , b ( x 1 ) + l n f w , b ( x 2 ) + l n ( 1 − f w , b ( x 3 ) ) + . . . + l n f w , b ( x n ) = ∑ n − [ y ^ n l n f w , b ( x n ) + ( 1 − y ^ n ) l n ( 1 − f w , b ( x n ) ) ] -lnL(w,b)=lnf_{w,b}(x_1)+lnf_{w,b}(x_2)+ln(1-f_{w,b}(x_3))+...+lnf_{w,b}(x_n)\\ =\sum_n -[\hat{y}^nlnf_{w,b}(x^n)+(1-\hat{y}^n)ln(1-f_{w,b}(x^n))] −lnL(w,b)=lnfw,b(x1)+lnfw,b(x2)+ln(1−fw,b(x3))+...+lnfw,b(xn)=n∑−[y^nlnfw,b(xn)+(1−y^n)ln(1−fw,b(xn))]
而这里我们记 C ( f ( x n ) , y ^ n ) = − [ y ^ n l n f w , b ( x n ) + ( 1 − y ^ n ) l n ( 1 − f w , b ( x n ) ) ] C(f(x^n),\hat{y}^n)=-[\hat{y}^nlnf_{w,b}(x^n)+(1-\hat{y}^n)ln(1-f_{w,b}(x^n))] C(f(xn),y^n)=−[y^nlnfw,b(xn)+(1−y^n)ln(1−fw,b(xn))],其实可以看出 C ( f ( x n ) , y ^ n ) C(f(x^n),\hat{y}^n) C(f(xn),y^n)是两个Bernouli分布的交叉熵(cross entropy)
1.2.2 交叉熵计算
H ( p , q ) = − ∑ x p ( x ) l n ( q ( x ) ) H(p,q)=-\sum_x p(x)ln(q(x)) H(p,q)=−∑xp(x)ln(q(x))
代表两个分布的接近程度

到这里Logistic regression的极小化就可以写为 L ( f ) = ∑ n C ( f ( x n ) , y ^ n ) L(f)=\sum_nC(f(x^n),\hat{y}^n) L(f)=∑nC(f(xn),y^n),
仔细观察这个式子可以发现,由上面的叙述可知, C ( f ( x n ) , y ^ n ) C(f(x^n),\hat{y}^n) C(f(xn),y^n)定义的是两种分布的交叉熵,也就是 f ( x n ) f(x^n) f(xn)和 y ^ n \hat{y}^n y^n这两种分布的交叉熵,而交叉熵表达了两种分布的相似程度,越接近0表示越相似,那么 L ( f ) L(f) L(f)的极小化也就等价于:
选择合适的参数 w , b w,b w,b使得估计的 f ( x n ) f(x^n) f(xn)和实际的 y ^ n \hat{y}^n y^n的分布尽量接近。
1.3 凸优化
采用随机梯度下降法不断更新 w w w和 b b b的值,以获取最优解。
1.4 logistic regression和linear regression的区别
1.4.1 区别
虽然logistic regression和linear regression更新参数的公式一样,但实际上 y ^ n \hat{y}^n y^n和 f w , b ( x n ) f_{w,b}(x^n) fw,b(xn)的取值是不一样的, y ^ n \hat{y}^n y^n和 f w , b ( x n ) f_{w,b}(x^n) fw,b(xn)可以是任何值, f w , b f_{w,b} fw,b也不同。
1.4.2 loss函数
logistic regression和linear regression的loss函数为什么不一样(为什么logistic regression 不采用 square error而要用cross entropy)?:
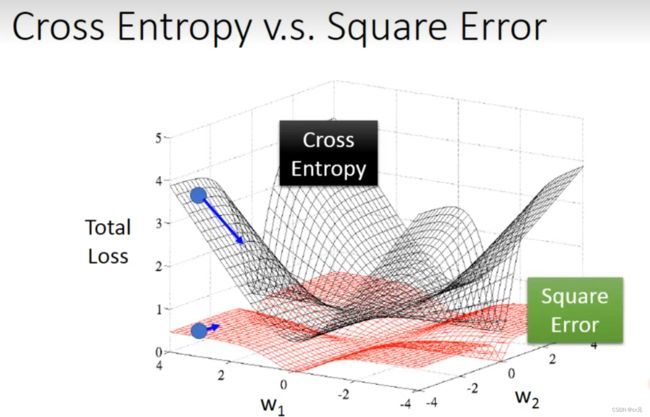
如下图所示,对逻辑回归来说,黑色为cross entropy,红色为squre error。可以看出,se在边缘地区梯度下降非常平缓,基本上和中心地区梯度变化一致,所以当梯度下降很慢时,无法确定是否已经优化到最优值(即是否在中心区域);但对于cross entropy,边远地区梯度下降幅度很大,中心区域(最优值区域)梯度下降平缓,所以当梯度不再明显变化时可以很好的确定此处就是参数最优取值。
2.generative和discriminative区别:
generative eg.naive bayes:
discriminative: logistic regression
实际上这两种model的function set一模一样,对 P ( C 1 ∣ x ) P(C_1|x) P(C1∣x)的估计都是 P ( C 1 ∣ x ) = σ ( w ⋅ x + b ) P(C_1|x)=\sigma(w \cdot x+b) P(C1∣x)=σ(w⋅x+b)
不一样的地方在于,generative model预先假设数据分布符合某个概率模型例如gaussian或bernouli,根据模型假设来求 w w w和 b b b的值;而logistic regression并没有这种假设,直接求取 w w w和 b b b的值。

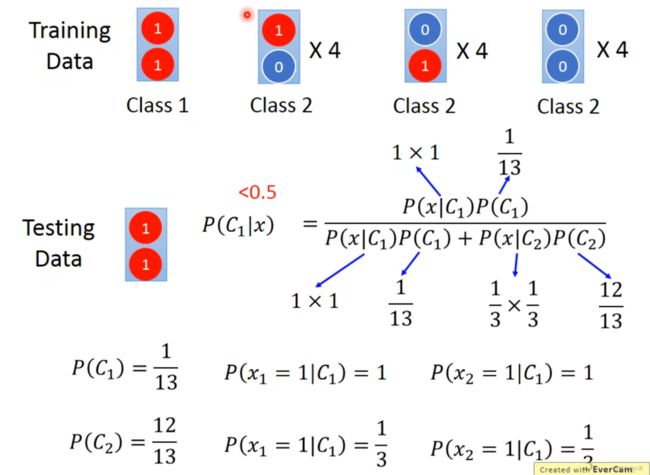
实例如下,按照generative model,(1,1)反而会被划分为class 2.
思考一下可以发现,实际上对于class 2的训练数据,三组数据的x1和x2可以随意互换,并不会影响条件概率,例如改成[ (1,1)*4,(0,0)*4,(0,0)*4 ],即class 2的前两组数据的x2值互换,并不影响其条件概率.