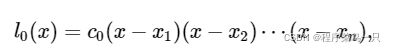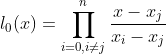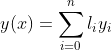matlab插值：拉格朗日插值

拉格朗日插值即对所要插值的函数进行拉格朗日多项式拟合

这是matlab插值系列的第二期，第一期：[数值分析拟合]Matlab三次样条插值拟合数据

（以后会有时间的时候再更新更多的插值方法）

这篇文章我推导过程参考过了一些其他文章，代码是自己写的，如有不对或者公式打错了欢迎批评指正

首先，对于所需要插值的自变量x和所需插值的数据点y:

一、我们先来了解它的插值原理：

        对于在一组数值散点中的任意一点进行插值，找到一个满足相应条件的n次多项式，我们希望能用所有点的函数值去表示它，并且每一点的函数值都与原来的函数值相符合。

        因此，设原数据的每一个点的函数值为,为了组成插值所得到的,前面配凑的系数是，那么则有：

        记从0开始推导，则
        

        那么由两个点的插值开始，所得的应当是线性插值

则有  那么显然有

对于中间的每一个点，都应当有

整理得到

那么从0开始，则其插值的系数为

, 有

这时，规律不够明显， 因此我们采用更多的点来进行相关的推导

当点的个数为n+1时,为了保证依然成立

首先，为了保证下方条件，分子为

 （图片来自参考文章

拉格朗日（Lagrange）插值多项式的基函数构造法(详细推导)）

此时，根据,可以有n+1个方程，那么由于有n+1个c(c0,c1,c2....cn)，则可通过解方程唯一确定对应的c0,解出c0后，即可确定

,

通过以上的公式推导，下面使用MATLAB来实现上述的计算内容

先加上我在里面调用的len.m

%返回一维数组长度(行数或列数其中大的一个，必须是一位数组)
function [length]=len(A)

    s=size(A);
    if s(2)==1
        length=s(1); %取行
    end
    if s(1)==1
        length=s(2);
    end
    if s(1)~=1 && s(2)~=1
        disp('必须是单行向量或单列向量')
        return
    end
            
end

编写函数     Lagrange.m计算拉格朗日插值:

其中许多的注释我用英语写的看着别嫌麻烦哈，这段时间为了学英语我也在天天头皮发麻）   

% *** Lagrange  interpolation ***
function L = Lagrange(x,y,x_2)
% x --origional x vector
% y --origional y vector need to be interpolated
% x_2 --the vector x that you want to interpolate to 
% author:FriedParrot   --2022-2-4
if len(x) ~= len(y)
    error('The length of x and y should be correspond');
end

xi = x_2;  %  generate the vector that need to be interpolated
% define the initial vectors
L = zeros(1,len(xi));

for i = 1:1:len(xi)  % This is the index of the xi(to be interpolated)
    l = ones(1,len(x));  % it is used every time
    for k = 1:1:len(x)
        for j= 1:1:len(x)
            if j ~= k  % similar to prod but the denominator shouldn't be zero
                l(k) = l(k) * ( xi(i)-x(j)) / (x(k)-x(j));
                % the index should be k --the first index of the iteration
            end
        end % cacultte the l_j
        L(i) = L(i) + l(k)*y(k);  % just for every single loop of s
    end
end

if nargout == 0
    figure('name','Lagrange Interpolation');
    plot(xi,L);
end

end

下面加上测试代码以及效果：

（代码使用外插值，即公式中的范围比数据的范围更广）

x = [1,2,4,6,8,9];
y =  cos(x);
x_2 = 0:0.05:10;
Lagrange(x,y,x_2);

插值效果： 

 

参考文章：

拉格朗日（Lagrange）插值多项式的基函数构造法(详细推导)

mathworld里关于Lagrange插值的简介（用软件可以进）

《专题一：插值法（1）拉格朗日插值法》