人工智能及其应用——第四章学习笔记(上)
人工智能及其应用
第四章 非经典推理
第三章讨论的消解反演推理、消解演绎推理和规则演绎推理等推理方法,都是确定性推理。它们建立在经典逻辑基础上,运用确定性知识进行精确推理,也是一种单调性推理。
现实世界中遇到的问题和事物间的关系,往往比较复杂,客观事物存在的随机性、模糊性、不完全性和不精确性,往往导致人们认识上一定程度的不确定性。
为此,需要在不完全和不确定的情况下运用不确定知识进行推理,即进行不确定性推理,包括(贝叶斯推理、概率推理、可信度方法和证据理论等)
4.1 经典推理和非经典推理
传统人工智能即逻辑学派是建立在符号逻辑推理的基础上的。逻辑涉及思维的规范,而推理则于思维的法则有关
人工智能从学科本身出发,对逻辑给予相应的界定:
- 人工智能把逻辑作为描述和模拟思维的工具,而不像逻辑学家那样研究逻辑理论,而是研究应用逻辑
- 人工智能不仅要把逻辑应用于学科研究,而且要探究逻辑的应用问题
- 人工智能把逻辑作为重视和模拟智能的手段,而不像数学家那样把逻辑作为改造和发展数学的基础
一般提到的逻辑有形式逻辑和数理逻辑。长期以来,形式逻辑和数理逻辑的研究和应用一直处于主导地位
人们把新产生的逻辑学派称为非经典推理,其相应的推理方法则叫做非经典推理。与此相应地把传统的逻辑学派及其推理方法称为经典逻辑和经典推理
可从如下五点来说明非经典逻辑和非经典推理与经典逻辑和经典推理的区别:
- 在推理方法上,经典逻辑采用演绎逻辑推理,而非经典逻辑采用归纳逻辑推理
- 在辖域取值上,经典逻辑都是二值逻辑(只有真和假两种),而非经典逻辑都是多值逻辑
- 在运算法则上,属于经典逻辑的形式逻辑和数理逻辑,它们的许多运算法则在非经典逻辑中就不能成立
- 在逻辑算符上,非经典逻辑具有更多的逻辑算符(非经典逻辑引用了附加算符(模态算符或算子))
- 在是否单调上,经典逻辑是单调的。引用非单调逻辑进行非单调推理是非经典逻辑与经典逻辑的又一重要区别
4.2 不确定性推理
不确定性推理也称不精确推理,是一种建立在非经典逻辑基础上的基于不确定性知识的推理,它从不确定性的初始证据出发,通过运用不确定性知识,推出具有一定程度的不确定性的和合理的近乎合理的结论
4.2.1 不确定性的表示与量度
不确定性的表示
不确定性推理中存在三种不确定性,即关于知识的不确定性、关于证据的不确定性和关于结论的不确定性。它们都具有相应的表示方法和量度标准
- 知识不确定性的表示
在不确定性推理中,由于知识都具有不确定性,所以必须采用适当的方法把知识的不确定性及不确定的程度表示出来
在确立不确定性的表示方法时,有两个直接相关的因素需要考虑:一是要能根据领域问题特征把其不确定性比较准确地描述出来;二是要便于在推理过程中推算不确定性 - 证据不确定性的表示
观察事物时所了解的事实往往具有某种不确定性,这种观察时产生的不确定性会导致证据的不确定性。
在推理中,有两种来源的证据:一种是用户在求解问题时提供的初始证据;另一种是在推理中用前面推出的结论作为当前推理的证据 - 结论不确定性的表示
由于使用知识和证据具有的不确定性,使得出的结论也具有不确定性。这种结论的不确定性也叫做规则的不确定性,它表示当规则的条件被完全满足时,产生某种结论的不确定程度
不确定性的量度
需要采用不同的数据和方法来量度确定性的程度。首先必须确定数据的取值范围
在确定量度方法及其范围时,必须注意到:
- 量度要能充分表达相应知识和证据不确定性的程度
- 量度范围的指定应便于领域专家和用户对不确定性的估计
- 量度要便于对不确定性的传递进行计算,而且对结论算出的不确定性量度不能超出量度规定的范围
- 量度的确定应当是直观的,并有相应的理论依据
4.2.2 不确定性的算法
不确定性的匹配算法
在确定性推理中,知识是否匹配成功是很容易确定的。但在不确定性推理中,由于知识和证据都具有不确定性,而且知识所要求的不确定性程度与证据实际具有的不确定性程度不一定相同,因而就出现了“怎样才算匹配成功”的问题
对于这个问题,目前常用的解决方法是:设计一个用来计算匹配双方相似程度的算法,再指定一个相似的限度,用来衡量匹配双方相似的程度是否落在指定的限度内
- 如果落在指定的限度内,就称它们是可匹配的,相应的知识可被应用
- 否则就称它们是不可匹配的,相应的知识不可应用
这种方法称为不确定性匹配算法,相似的限度称为阈值
不确定性的更新算法
在不确定性推理的过程中还需要解决不确定性的更新问题,即在推理过程中如何考虑知识不确定性的动态积累和传递。
不确定性的更新算法一般包括如下算法:
- 已知规则前提即证据 E E E的不确定性 C ( E ) C(E) C(E)和规则的强度 f ( H , E ) f(H,E) f(H,E),其中 H H H表示假设,试求 H H H的不确定性 C ( H ) C(H) C(H)。即定义算法 g 1 g_1 g1,使得:
C ( H ) = g 1 [ C ( E ) , f ( H , E ) ] C(H)=g_1\left[C(E),f(H,E) \right] C(H)=g1[C(E),f(H,E)] - 并行规则算法。 根据独立的证据 E 1 E_1 E1和 E 2 E_2 E2,分别求得假设 H H H的不确定性为 C 1 ( H ) C_1(H) C1(H)和 C 2 ( H ) C_2(H) C2(H)。求出证据 E 1 E_1 E1和 E 2 E_2 E2的组合导致结论 H H H的不确定性 C ( H ) C(H) C(H),即定义算法 g 2 g_2 g2,使得
C ( H ) = g 2 [ C 1 ( H ) , C 2 ( H ) ] C(H)=g_2\left[C_1(H),C_2(H) \right] C(H)=g2[C1(H),C2(H)] - 证据合取的不确定性算法。 根据两个证据 E 1 E_1 E1和 E 2 E_2 E2的不确定性值 C ( E 1 ) C(E_1) C(E1)和 C ( E 2 ) C(E_2) C(E2),求出证据 E 1 E_1 E1和 E 2 E_2 E2合取的不确定性,即定义算法 g 3 g_3 g3,使得
C ( E 1 A N D E 2 ) = g 3 [ C ( E 1 ) , C ( E 2 ) ] C(E_1\ AND\ E_2)=g_3\left[C(E_1),C(E_2) \right] C(E1 AND E2)=g3[C(E1),C(E2)] - 证据析取的不确定性算法。 根据两个证据 E 1 E_1 E1和 E 2 E_2 E2的不确定性值 C ( E 1 ) C(E_1) C(E1)和 C ( E 2 ) C(E_2) C(E2),求出证据 E 1 E_1 E1和 E 2 析 取 的 不 确 定 性 , 即 定 义 算 法 E_2析取的不确定性,即定义算法 E2析取的不确定性,即定义算法g_4$,使得
C ( E 1 O R E 2 ) = g 4 [ C ( E 1 ) , C ( E 2 ) ] C(E_1\ OR\ E_2)=g_4\left[C(E_1),C(E_2) \right] C(E1 OR E2)=g4[C(E1),C(E2)]
证据合取和证据析取的不确定算法统称为组合证据的不确定性算法。实际上,规则的前提可以是用 A N D AND AND和 O R OR OR把多个条件连接起来构成的复合事件
目前,关于组合证据的不确定性的计算已经提出了多种方法,其中用得较多的有如下几种:
- 最大最小法
C ( E 1 A N D E 2 ) = m i n { C ( E 1 ) , C ( E 2 ) } C ( E 1 O R E 2 ) = m a x { C ( E 1 ) , C ( E 2 ) } C(E_1\ AND\ E_2)=min\left\{C(E_1),C(E_2) \right\} \\ C(E_1\ OR\ E_2)=max\left\{C(E_1),C(E_2) \right\} C(E1 AND E2)=min{C(E1),C(E2)}C(E1 OR E2)=max{C(E1),C(E2)} - 概率方法(只能在事件之间完全独立时使用)
C ( E 1 A N D E 2 ) = C ( E 1 ) C ( E 2 ) C ( E 1 O R E 2 ) = C ( E 1 ) + C ( E 2 ) − C ( E 1 ) C ( E 2 ) C(E_1\ AND\ E_2)=C(E_1)C(E_2) \\ C(E_1\ OR\ E_2)=C(E_1)+C(E_2)-C(E_1)C(E_2) C(E1 AND E2)=C(E1)C(E2)C(E1 OR E2)=C(E1)+C(E2)−C(E1)C(E2) - 有界方法
C ( E 1 A N D E 2 ) = m a x { 0 , C ( E 1 ) + C ( E 2 ) − 1 } C ( E 1 O R E 2 ) = m i n { 1 , C ( E 1 ) + C ( E 2 ) } C(E_1\ AND\ E_2)=max\left\{0,C(E_1)+C(E_2)-1 \right\} \\ C(E_1\ OR\ E_2)=min\left\{1,C(E_1)+C(E_2) \right\} C(E1 AND E2)=max{0,C(E1)+C(E2)−1}C(E1 OR E2)=min{1,C(E1)+C(E2)}
上述的每一组公式都有相应的适用范围和使用条件
4.3 概率推理
上面讨论了不确定性推理要解决的一些主要问题。不过,并非任何一个不确定性推理都必须包括上述各项内容,而且在不同的不确定性推理模型中,这些问题的解决方法是各不相同的。
目前用得较多的不精确推理模型有:
概率推理、可信度方法、证据理论、贝叶斯推理和模糊推理等
4.3.1 概率的基本性质和计算公式(详细参考《概率论与数理统计》)
- 随机事件、必然事件、互斥事件、独立事件等
- 相关概率公式(全概率公式、贝叶斯公式等)
4.3.2 概率推理方法
设有如下产生式规则:
I F E T H E N H IF\qquad E\qquad THEN\qquad H IFETHENH
则证据(或前提条件) E E E不确定性的概率为 P ( E ) P(E) P(E),概率方法不精确推理的目的就是求出在证据 E E E下结论 H H H发生的概率 P ( H ∣ E ) P(H|E) P(H∣E)
把贝叶斯方法用于不精确推理的一个原始条件是:已知前提 E E E的概率 P ( E ) P(E) P(E)和 H H H的先验概率 P ( H ) P(H) P(H),并已知 H H H成立时 E E E出现的条件概率 P ( E ∣ H ) P(E|H) P(E∣H)。如果只使用这一条规则作进一步推理,则使用如下最简形式的贝叶斯公式便可以从 H H H的先验概率 P ( H ) P(H) P(H)推得 H H H的后验概率:
P ( H ∣ E ) = P ( E ∣ H ) P ( H ) P ( E ) (4.13) P(H|E)=\frac{P(E|H)P(H)}{P(E)} \tag{4.13} P(H∣E)=P(E)P(E∣H)P(H)(4.13)
若一个证据 E E E支持多个假设 H 1 , H 2 , ⋯ , H n H_1,H_2,\cdots,H_n H1,H2,⋯,Hn,则可得如下贝叶斯公式:
P ( H i ) P ( E ∣ H i ) ∑ j = 1 n P ( H j ) P ( E ∣ H j ) , i = 1 , 2 , ⋯ , n \frac{P(H_i)P(E|H_i)}{\sum\limits^n_{j=1}P(H_j)P(E|H_j)},\quad i=1,2,\cdots,n j=1∑nP(Hj)P(E∣Hj)P(Hi)P(E∣Hi),i=1,2,⋯,n
若有多个证据 E 1 , E 2 , ⋯ , E m E_1,E_2,\cdots,E_m E1,E2,⋯,Em和多个结论 H 1 , H 2 , ⋯ , H n H_1,H_2,\cdots,H_n H1,H2,⋯,Hn,并且每个证据都以一定程度支持结论,则:
P ( H i ∣ E 1 E 2 ⋯ E m ) = P ( E 1 ∣ H i ) P ( E 2 ∣ H i ) ⋯ P ( E m ∣ H i ) P ( H i ) ∑ j = 1 n P ( E 1 ∣ H j ) P ( E 2 ∣ H j ) ⋯ P ( E m ∣ H j ) P ( H j ) P(H_i|E_1E_2\cdots E_m)=\frac{P(E_1|H_i)P(E_2|H_i)\cdots P(E_m|H_i)P(H_i)}{\sum\limits^n_{j=1}P(E_1|H_j)P(E_2|H_j)\cdots P(E_m|H_j)P(H_j)} P(Hi∣E1E2⋯Em)=j=1∑nP(E1∣Hj)P(E2∣Hj)⋯P(Em∣Hj)P(Hj)P(E1∣Hi)P(E2∣Hi)⋯P(Em∣Hi)P(Hi)
这时,只要已知 H i H_i Hi的先验概率 P ( H i ) P(H_i) P(Hi)即 H i H_i Hi成立时证据 E 1 , E 2 , ⋯ , E m E_1,E_2,\cdots,E_m E1,E2,⋯,Em出现的条件概率 P ( E 1 ∣ H i ) ⋯ P ( E m ∣ H i ) P ( H i ) P(E_1|H_i)\cdots P(E_m|H_i)P(H_i) P(E1∣Hi)⋯P(Em∣Hi)P(Hi),就可利用上述公式计算出在 E 1 , E 2 , ⋯ , E m E_1,E_2,\cdots,E_m E1,E2,⋯,Em出现情况下 H i H_i Hi条件概率 P ( H i ∣ E 1 E 2 ⋯ E m ) P(H_i|E_1E_2\cdots E_m) P(Hi∣E1E2⋯Em)
概率推理方法具有较强的理论基础和较好的数学描述。当证据和结论彼此独立时,计算不很复杂。但是,应用这种方法时要求给出结论 H i H_i Hi的先验概率 P ( H i ) P(H_i) P(Hi)及证据 E j E_j Ej的条件概率 P ( E j ∣ H i ) P(E_j|H_i) P(Ej∣Hi),而要获得这些概率数据却是相当困难的。
此外,贝叶斯公式的应用条件相当严格,即要求各事件彼此独立。如果证据间存在依赖关系,那么就不能直接采用这种方法
4.4 主观贝叶斯方法
杜达 ( D u d a ) (Duda) (Duda)和哈特 ( H a r t ) (Hart) (Hart)等人在贝叶斯公式的基础上,与 1976 1976 1976年提出主观贝叶斯方法,建立了不精确推理模型
4.4.1 知识不确定性的表示
在主观贝叶斯方法中,用下列产生式规则表示知识:
I F E T H E N ( L S , L N ) H IF\qquad E \qquad THEN\qquad (LS,LN)\qquad H IFETHEN(LS,LN)H
式中, ( L S , L N ) (LS,LN) (LS,LN)表示知识的静态强度,称 L S LS LS为式成立的充分因子, L N LN LN为式成立的必要因子,它们分别衡量证据(前提) E E E对结论 H H H的支持程度和 ∼ E \sim E ∼E对 H H H的支持程度。定义:
L S = P ( E ∣ H ) P ( E ∣ ∼ H ) ( 4.17 ) L N = P ( ∼ E ∣ H ) P ( ∼ E ∣ ∼ H ) = 1 − P ( E ∣ H ) 1 − P ( E ∣ ∼ H ) ( 4.18 ) LS=\frac{P(E|H)}{P(E|\sim H)} \qquad (4.17)\\ LN=\frac{P(\sim E|H)}{P(\sim E|\sim H)}=\frac{1-P(E|H)}{1-P(E|\sim H)}\qquad (4.18) LS=P(E∣∼H)P(E∣H)(4.17)LN=P(∼E∣∼H)P(∼E∣H)=1−P(E∣∼H)1−P(E∣H)(4.18)
L S LS LS和 L N LN LN的取值范围为 [ 0 , + ∞ ) [0,+\infty) [0,+∞),其具体数值由领域专家决定
主观贝叶斯方法的不精确推理过程就是根据前提 E E E的概率 P ( E ) P(E) P(E),利用规则的 L S LS LS和 L N LN LN,把结论 H H H的先验概率 P ( H ) P(H) P(H)更新为后验概率 P ( H ∣ E ) P(H|E) P(H∣E)的过程
由式 ( 4.13 ) (4.13) (4.13)可知
P ( H ∣ E ) = P ( E ∣ H ) P ( H ) P ( E ) P ( ∼ H ∣ E ) = P ( E ∣ ∼ H ) P ( ∼ H ) P ( E ) P(H|E)=\frac{P(E|H)P(H)}{P(E)} \\ P(\sim H|E)=\frac{P(E|\sim H)P(\sim H)}{P(E)} P(H∣E)=P(E)P(E∣H)P(H)P(∼H∣E)=P(E)P(E∣∼H)P(∼H)
以上两式相除,可得
P ( H ∣ E ) P ( ∼ H ∣ E ) = P ( E ∣ H ) P ( E ∣ ∼ H ) ⋅ P ( H ) P ( ∼ H ) (4.19) \frac{P(H|E)}{P(\sim H|E)}=\frac{P(E|H)}{P(E|\sim H)}\cdot \frac{P(H)}{P(\sim H)} \tag{4.19} P(∼H∣E)P(H∣E)=P(E∣∼H)P(E∣H)⋅P(∼H)P(H)(4.19)
再定义概率函数为
O ( X ) = P ( X ) 1 − P ( X ) 或 O ( X ) = P ( X ) P ( ∼ X ) (4.20) O(X)=\frac{P(X)}{1-P(X)}\quad 或 \quad O(X)=\frac{P(X)}{P(\sim X)}\tag{4.20} O(X)=1−P(X)P(X)或O(X)=P(∼X)P(X)(4.20)
即 X X X的几率等于 X X X出现的概率与 X X X不出现的概率之比。由 ( 4.20 ) (4.20) (4.20)可知,随着 P ( X ) P(X) P(X)的增大, O ( X ) O(X) O(X)也在增大,且有
O ( X ) = { 0 , 若 P ( x ) = 0 + ∞ , 若 P ( X ) = 1 O(X)= \begin{cases} 0, \qquad \ 若P(x)=0\\ +\infty,\quad若P(X)=1 \end{cases} O(X)={0, 若P(x)=0+∞,若P(X)=1
这样,就可把取值为 [ 0 , 1 ] [0,1] [0,1]的 P ( X ) P(X) P(X)放大为取值 [ 0 , + ∞ ) [0,+\infty) [0,+∞)的 O ( X ) O(X) O(X)
把式 ( 4.20 ) (4.20) (4.20)的关系代入式 ( 4.19 ) (4.19) (4.19),可得
O ( H ∣ E ) = P ( E ∣ H ) P ( E ∣ ∼ H ) ⋅ O ( H ) O(H|E)=\frac{P(E|H)}{P(E|\sim H)}\cdot O(H) O(H∣E)=P(E∣∼H)P(E∣H)⋅O(H)
再把式 ( 4.17 ) (4.17) (4.17)代入上式,得
O ( H ∣ E ) = L S ⋅ O ( H ) (4.22) O(H|E)=LS\cdot O(H) \tag{4.22} O(H∣E)=LS⋅O(H)(4.22)
同理可得
O ( H ∣ ∼ E ) = L N ⋅ O ( H ) (4.23) O(H|\sim E)=LN\cdot O(H) \tag{4.23} O(H∣∼E)=LN⋅O(H)(4.23)
式 ( 4.22 ) (4.22) (4.22)和 ( 4.23 ) (4.23) (4.23)就是修改的贝叶斯公式。由这两式可知:当 E E E为真时,可利用 L S LS LS将 H H H的先验几率 O ( H ) O(H) O(H)更新为其后验几率 O ( H ∣ E ) O(H|E) O(H∣E);当 E E E为假时,可利用 L N LN LN将 H H H的先验几率 O ( H ) O(H) O(H)更新为其后验几率 O ( H ∣ ∼ E ) O(H|\sim E) O(H∣∼E)
4.4.2 证据不确定性的表示
主观贝叶斯方法中证据的不确定性也是用概率表示的
可信度 C ( E ∣ S ) C(E|S) C(E∣S)与概率 P ( E ∣ S ) P(E|S) P(E∣S)的对应关系如下:
- C ( E ∣ S ) = − 5 C(E|S)=-5 C(E∣S)=−5,表示在观察 S S S下证据肯定不存在,即 P ( E ∣ S ) = 0 P(E|S)=0 P(E∣S)=0
- C ( E ∣ S ) = 0 C(E|S)=0 C(E∣S)=0,表示 S S S与 E E E无关,即 P ( E ∣ S ) = P ( E ) P(E|S)=P(E) P(E∣S)=P(E)
- C ( E ∣ S ) = 5 C(E|S)=5 C(E∣S)=5,表示在观察 S S S下证据 E E E肯定存在,即 P ( E ∣ S ) = 1 P(E|S)=1 P(E∣S)=1
- C ( E ∣ S ) C(E|S) C(E∣S)为其他数时与 P ( E ∣ S ) P(E|S) P(E∣S)的对应关系,可通过对上述三点进行分段线性插值得到,如图
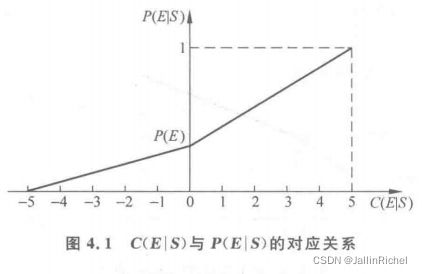
由图 4.1 4.1 4.1可求得:
P ( E ∣ S ) = { C ( E ∣ S ) + P ( E ) × ( 5 − C ( E ∣ S ) ) 5 , 若 0 ≤ C ( E ∣ S ) ≤ 5 P ( E ) × ( C ( E ∣ S ) + 5 ) 5 , 若 − 5 ≤ C ( E ∣ S ) ≤ 0 (4.24) \tag{4.24} P(E|S)= \begin{cases} \frac{C(E|S)+P(E)\times (5-C(E|S))}{5},\quad 若0\le C(E|S)\le 5\\ \\ \frac{P(E)\times (C(E|S)+5)}{5},\qquad\qquad 若-5\le C(E|S)\le 0 \end{cases}\\ P(E∣S)=⎩⎪⎨⎪⎧5C(E∣S)+P(E)×(5−C(E∣S)),若0≤C(E∣S)≤55P(E)×(C(E∣S)+5),若−5≤C(E∣S)≤0(4.24)
C ( E ∣ S ) = { 5 × P ( E ∣ S ) − P ( E ) 1 − P ( E ) , 若 P ( E ) ≤ P ( E ∣ S ) ≤ 1 5 × P ( E ∣ S ) − P ( E ) P ( E ) , 若 0 ≤ P ( E ∣ S ) ≤ P ( E ) (4.25) \tag{4.25} C(E|S)= \begin{cases} 5\times \frac{P(E|S)-P(E)}{1-P(E)},\qquad 若P(E)\le P(E|S)\le1 \\ \\ 5\times \frac{P(E|S)-P(E)}{P(E)},\qquad 若0\le P(E|S)\le P(E) \end{cases} C(E∣S)=⎩⎪⎨⎪⎧5×1−P(E)P(E∣S)−P(E),若P(E)≤P(E∣S)≤15×P(E)P(E∣S)−P(E),若0≤P(E∣S)≤P(E)(4.25)
由上面两式可见,只要用户对初始证据给出相应的可信度 C ( E ∣ S ) C(E|S) C(E∣S),系统就会把它转化为 P ( E ∣ S ) P(E|S) P(E∣S),也就相当于给出了证据 E E E的概率 P ( E ∣ S ) P(E|S) P(E∣S)
当证据不确定时,要用杜达等人证明的下列公式计算后验概率:
P ( H ∣ S ) = P ( H ∣ E ) P ( E ∣ S ) + P ( H ∣ ∼ E ) P ( ∼ E ∣ S ) (4.26) P(H|S)=P(H|E)P(E|S)+P(H|\sim E)P(\sim E|S) \tag{4.26} P(H∣S)=P(H∣E)P(E∣S)+P(H∣∼E)P(∼E∣S)(4.26)
- 当 P ( E ∣ S ) = 1 P(E|S)=1 P(E∣S)=1时, P ( ∼ E ∣ S ) = 0 , P ( H ∣ S ) = P ( H ∣ E ) P(\sim E|S)=0,P(H|S)=P(H|E) P(∼E∣S)=0,P(H∣S)=P(H∣E)
- 当 P ( E ∣ S ) = 0 P(E|S)=0 P(E∣S)=0时, P ( ∼ E ∣ S ) = 1 , P ( H ∣ S ) = P ( H ∣ ∼ E ) P(\sim E|S)=1,P(H|S)=P(H|\sim E) P(∼E∣S)=1,P(H∣S)=P(H∣∼E)
- 当 P ( E ∣ S ) = P ( E ) P(E|S)=P(E) P(E∣S)=P(E)时, P ( H ∣ S ) = P ( H ) P(H|S)=P(H) P(H∣S)=P(H)
当 P ( E ∣ S ) P(E|S) P(E∣S)为其他值时,通过分段线性插值即可得到计算 P ( H ∣ S ) P(H|S) P(H∣S)的公式:
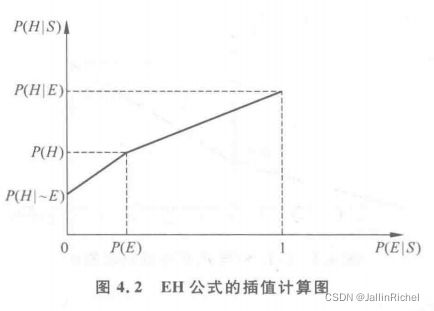
如图,函数的解析式为
P ( H ∣ S ) = { P ( H ∣ ∼ E ) + P ( H ) − P ( H − P ( H ∣ ∼ E ) P ( E ) × P ( E ∣ S ) , 若 0 ≤ P ( E ∣ S ) < P ( E ) P ( H ) + P ( H ∣ E ) − P ( H ) 1 − P ( E ) × [ P ( E ∣ S ) − P ( E ) ] , 若 P ( E ) ≤ P ( E ∣ S ) ≤ 1 (4.27) \tag{4.27} P(H|S)= \begin{cases} P(H|\sim E)+\frac{P(H)-P(H-P(H|\sim E)}{P(E)}\times P(E|S),\qquad 若0\le P(E|S)
并称其为 E H EH EH公式
将 ( 4.24 ) (4.24) (4.24)代入式 ( 4.27 ) (4.27) (4.27),可得:
P ( H ∣ S ) = { P ( H ∣ ∼ E ) + [ P ( H ) − P ( H ∣ ∼ E ) ] × [ 1 5 C ( E ∣ S ) + 1 ] , 若 C ( E ∣ S ) ≤ 0 P ( H ) + [ P ( H ∣ E ) − P ( H ) ] × 1 5 C ( E ∣ S ) , 若 C ( E ∣ S ) > 0 (4.28) \tag{4.28} P(H|S)= \begin{cases} P(H|\sim E)+[P(H)-P(H|\sim E)]\times[\frac{1}{5}C(E|S)+1],\qquad 若C(E|S)\le0 \\ \\ P(H)+[P(H|E)-P(H)]\times \frac{1}{5}C(E|S),\qquad 若C(E|S)>0 \end{cases} P(H∣S)=⎩⎪⎨⎪⎧P(H∣∼E)+[P(H)−P(H∣∼E)]×[51C(E∣S)+1],若C(E∣S)≤0P(H)+[P(H∣E)−P(H)]×51C(E∣S),若C(E∣S)>0(4.28)
并称其为 C P CP CP公式
4.4.3 主观贝叶斯方法的推理过程
当采用初始证据进行推理时,通过提问用户得到 C ( E ∣ S ) C(E|S) C(E∣S),通过 C P CP CP公式就可求出 P ( H ∣ S ) P(H|S) P(H∣S)。当采用推理过程中得到的中间结论作为证据进行推理时,通过 E H EH EH公式可求得 P ( H ∣ S ) P(H|S) P(H∣S)
如果有 n n n条知识都支持同一结论 H H H,而且每条知识的前提条件分别是 n n n个相互独立的证据 E 1 , E 2 , ⋯ , E n E_1,E_2,\cdots,E_n E1,E2,⋯,En,而这些证据又分别与观察 S 1 , S 2 , ⋯ , S n S_1,S_2,\cdots,S_n S1,S2,⋯,Sn相对应,这时,首先对每条知识分别求出 H H H的后验几率 O ( H ∣ S i ) O(H|S_i) O(H∣Si),然后按下述公式求出所有观察下 H H H的后验几率:
O ( H ∣ S 1 , S 2 , ⋯ , S n ) = O ( H ∣ S 1 ) O ( H ) × O ( H ∣ S 2 ) O ( H ) × ⋯ × O ( H ∣ S n ) O ( H ) × O ( H ) O(H|S_1,S_2,\cdots,S_n)=\frac{O(H|S_1)}{O(H)}\times\frac{O(H|S_2)}{O(H)}\times\cdots\times\frac{O(H|S_n)}{O(H)}\times O(H) O(H∣S1,S2,⋯,Sn)=O(H)O(H∣S1)×O(H)O(H∣S2)×⋯×O(H)O(H∣Sn)×O(H)
主观贝叶斯方法具有下列优点:
- 主观贝叶斯方法的计算公式大多是在概率论的基础上推导出来的,具有比较坚实的理论基础
- 规则的 L S LS LS和 L N LN LN是由领域专家根据实践经验给出的,避免了大量的数据统计工作。此外,它比较全面地反映了证据与结论间的因果关系,符合现实世界中某些领域的实际情况,使推出的结论具有比较准确的确定性
- 主观贝叶斯方法不仅给出了在证据确定情况下由 H H H的先验概率更新为后验概率的方法,也给出了在证据不确定情况下更新先验概率为后验概率的方法
主观贝叶斯方法的一些缺点:
- 它要求领域专家在给出规则的同时,给出 H H H的先验概率 P ( H ) P(H) P(H),这是比较困难的
- 贝叶斯定理中关于事件间独立性的要求使主观贝叶斯方法的应用受到一定限制