机器学习基础学习-scikit-learn中的多项式回归和pipeline

前言

在上一篇博客机器学习基础学习-多项式回归当中，主要在调用线性回归前，改造了X，添加了X² 的特征，这个整个多项式回归的过程在sklearn当中封装在了preprocessing的包中，主要作用是对数据的预处理（就是为我们的数据添加新的特征），这里import一个PolynomialFeatures类

1、scikit-learn中的多项式回归（一个特征）

（1）生成样本数据
和上一篇博客一样，首先生成我们的样本数据

# scikit-learn中的多项式回归于pipeline
import numpy as np
import matplotlib.pyplot as plt

# 生成随机数据
# random.uniform(x, y)方法将随机生成一个实数，它在 [x,y] 范围内。
x = np.random.uniform(-3, 3, size = 100)
X = x.reshape(-1, 1) # shape：（100,1）

# np.random.normal()正态分布的噪音
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size = 100)

（2）引入PolynomialFeatures类并调用

from sklearn.preprocessing import PolynomialFeatures
# 实例化对象
# degree表示要为原本的数据集添加最多几次幂相应的特征
np.poly = PolynomialFeatures(degree=2)

我们之前进行多项式回归的时候，本来的特征相当于一次幂，我们的操作相当于添加了2次幂的特征

（3）训练并得到转换后的特征值矩阵

# 训练
poly.fit(X)
# 特征值的转换
X2 = poly.transform(X)

但是这里我们打印一下X2的维度print(X2.shape, 'X2.shape')发现这是个100行，3列的数据，和之前实现的只增加X² 这个特征值的情况不一样（这种情况相比原数据只增加了一列对应X² 特征值），

打印一下X2矩阵

发现这里在第一列加入了1.00的数据，这里其实可以看成是他自动为我们加入了X⁰ 的一列数据，对应它的第二列对应X¹ 特征，第三列对应X² 特征。

由此我们就通过PolynomialFeatures获取了多项式特征相应的数据集

（4）引入LinearRegression类并训练、绘制曲线
在得到我们转换后的特征值矩阵后，我们引入sklearn中的LinearRegression类，对我们的样本进行训练，然后拟合出相应的曲线。

from sklearn.linear_model import LinearRegression
'''
  线性回归拟合数据集
  这里调用sklearn的LinearRegression类
'''
# 实例化新对象
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
print(y_predict2, 'y_predict2多项式回归预测结果')
# 绘制多项式回归，预测后的结果
plt.scatter(x, y)
# 直接绘制，会导致图像错乱，因为x，y的值没有按照大小顺序排序
# plt.plot(x, y_predict2, color='r')
# argsort()函数是将x中的元素从小到大排列，提取其对应的index(索引)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()

得到的这一结果和上一篇博客中的结果也是一致的。
同样，这里打印出我们的系数矩阵print(lin_reg2.coef_, 'lin_reg2.coef系数')

对比我们生成样本的函数y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size = 100)
这里的三列分别对应x⁰ 、x¹ 、x² 的系数。
同理查看截距print(lin_reg2.intercept_, 'lin_reg2.intercept_截距')

对比我们生成样本的函数y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size = 100)，截距也是吻合的。

2、scikit-learn中的多项式回归（两个特征）

（1）生成样本数据

import numpy as np

# 生成数据集
X = np.arange(1, 11).reshape(-1, 2) # arange函数用于创建等差数组，从1-10取值，设置成5行两列的矩阵

可以把我们的矩阵打印出来看一下

（2）实例化对象并得到转换后的特征矩阵

from sklearn.preprocessing import PolynomialFeatures
# 实例化对象
# degree表示要为原本的数据集添加最多几次幂相应的特征
poly = PolynomialFeatures(degree=2)
# 训练
poly.fit(X)
# 特征值的转换
X2 = poly.transform(X)

将本来的X的数据集转换成了最多包含二次幂X² 的数据集。我们打印一下X2，或者用shape看一下，可以发现X2转换成了5行6列的矩阵

这里的第一列仍然是对应我们的X⁰ ,第二列和第三列对应我们原来的X矩阵（2列一次幂的项）。
剩下的三列对应我们的二次幂的特征，其中第四列[1,9,25,49,81]对应X的第一列平方的特征，第六列[4,16,36,64,100]对应X的第二列平方的特征。剩下的第五列则是X中的两列相乘的结果。
小总结：对于二次幂的特征，如果我们原来有X1、X2两个特征，最终我们会生成3列二次幂的特征：分别是X1² ,X2² ,X1*X2.

3、scikit-learn中的多项式回归（三个特征）

# 实例化对象(degree=3)
# degree表示要为原本的数据集添加最多几次幂相应的特征
poly2 = PolynomialFeatures(degree=3)
# 训练
poly2.fit(X)
# 特征值的转换
X3 = poly2.transform(X)
print(X3.shape, 'X3.shape')

我们将degree设置成3,我们打印一下X3.shape

发现此时X3变成了5行10列的矩阵，分析一下他们的组成

所以X3的10列分别是上述三项，包含了每次幂的每种组成情况
增大我们传入的degree经过PolynomialFeatures后，这里的项数会成指数倍的增长，这样的特性让PolynomialFeatures涉及到了所有次幂的所有可能性。

4、scikit-learn中的多项式回归涉及到的所有代码

# scikit-learn中的多项式回归（一个特征值）
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

# 生成随机数据
# random.uniform(x, y)方法将随机生成一个实数，它在 [x,y] 范围内。
x = np.random.uniform(-3, 3, size = 100)
X = x.reshape(-1, 1) # shape：（100,1）

# np.random.normal()正态分布的噪音
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size = 100)

# 实例化对象
# degree表示要为原本的数据集添加最多几次幂相应的特征
poly = PolynomialFeatures(degree=2)
# 训练
poly.fit(X)
# 特征值的转换
X2 = poly.transform(X)



'''
  线性回归拟合数据集
  这里调用sklearn的LinearRegression类
'''
# 实例化新对象
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
# 绘制多项式回归，预测后的结果
plt.scatter(x, y)
# 直接绘制，会导致图像错乱，因为x，y的值没有按照大小顺序排序
# plt.plot(x, y_predict2, color='r')
# argsort()函数是将x中的元素从小到大排列，提取其对应的index(索引)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()

print(lin_reg2.coef_, 'lin_reg2.coef系数')
print(lin_reg2.intercept_, 'lin_reg2.intercept_截距')

# scikit-learn中的多项式回归（多个特征值）
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

# 生成数据集
X = np.arange(1, 11).reshape(-1, 2) # arange函数用于创建等差数组，从1-10取值，设置成5行两列的矩阵



# # 实例化对象(degree=2)
# # degree表示要为原本的数据集添加最多几次幂相应的特征
# poly = PolynomialFeatures(degree=2)
# # 训练
# poly.fit(X)
# # 特征值的转换
# X2 = poly.transform(X)
# print(X2)




# 实例化对象(degree=3)
# degree表示要为原本的数据集添加最多几次幂相应的特征
poly2 = PolynomialFeatures(degree=3)
# 训练
poly2.fit(X)
# 特征值的转换
X3 = poly2.transform(X)
print(X3.shape, 'X3.shape')

5、pipeline

pipeline的英文名称是管道，回顾一下之前多项式回归的过程，
1、对于原始的样本数据，我们需要通过PolynomialFeatures这个类生成相应的多项式的特征的样本数据。
2、之前进行多项式回归，将生成的多项式样本数据直接送给了LinearRegression进行训练，但如果degree特别大，这些样本生成的特征的数据之间的差异会很大（例如degree=100，1¹ 和10¹⁰⁰ 之间的差异就很大 ）。
3、进行线性回归时，如果用梯度下降法搜索相应的结果，由于数据分布太不均衡会导致搜索过程很慢，就应该使用一下数据的归一化，然后送给线性回归。

如果使用pipeline，就可以将上面的三步合在一起，使得每次调用的时候不用不停重复着三步
下面是代码实现

# pipeline

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression

# 生成随机数据
# random.uniform(x, y)方法将随机生成一个实数，它在 [x,y] 范围内。
x = np.random.uniform(-3, 3, size = 100)
X = x.reshape(-1, 1) # shape：（100,1）

# np.random.normal()正态分布的噪音
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size = 100)

# 使用pipeline创建管道，送给poly_reg对象的数据会沿着管道的三步依次进行
poly_reg = Pipeline([ # Pipeline传入的是列表，列表中传入管道中每一步对应的类(这个类以元组的形式进行传送)
  ("poly", PolynomialFeatures(degree=2)), # 第一步：求多项式特征，相当于poly = PolynomialFeatures(degree=2)
  ("std_scaler", StandardScaler()), # 第二步：数值的均一化
  ("lin_reg", LinearRegression()) # 第三步：进行线性回归操作
])

# 将X送给poly_reg执行前两步操作，得到的全新的数据x会送给LinearRegression进行fit相应的操作
poly_reg.fit(X, y)
# predict操作也同上
y_predict = poly_reg.predict(X)

# 绘制
plt.scatter(x, y)
# 直接绘制，会导致图像错乱，因为x，y的值没有按照大小顺序排序
# plt.plot(x, y_predict2, color='r')
# argsort()函数是将x中的元素从小到大排列，提取其对应的index(索引)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()

运行结果

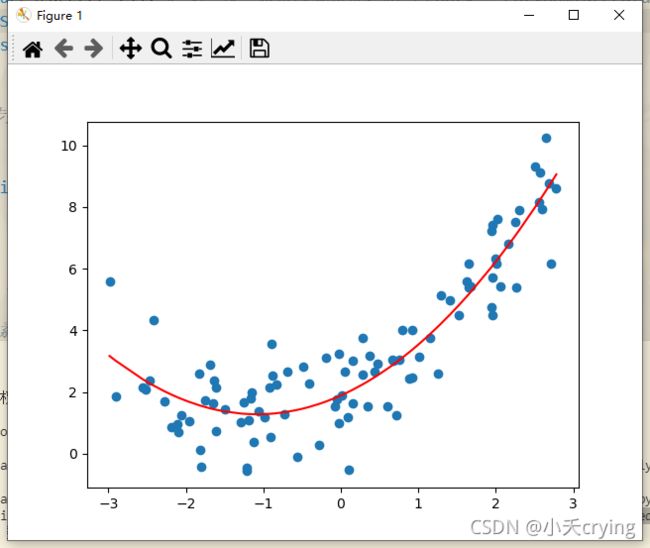
我们使用pipeline创建一个多项式回归的对象，对我们的数据进行预测，得到了和之前一致的曲线。

有了多项式回归这样的武器，我们可以很方便的对非线性的数据进行拟合