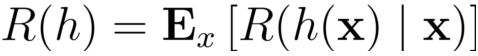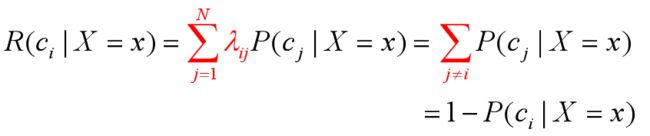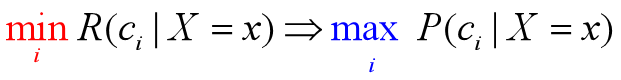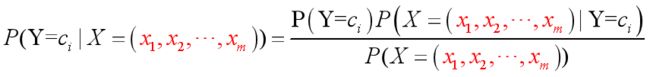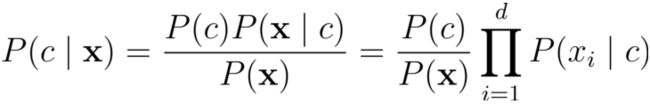机器学习 贝叶斯分类器 拉普拉斯修正
文章目录
-
-
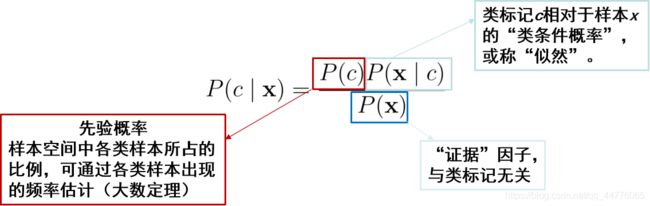
- 1. 贝叶斯决公式
- 2. 使用西瓜数据集
- 3. 朴素贝叶斯
- 3. 拉普拉斯修正
- 4. 代码
- 5. 结果
-
-
- 5.1 训练数据集
- 5.2 训练数据集
- 5.3 结果
-
- 6. 参考书籍
-
在分类问题情况下,在所有相关概率都已知的理想情形下,贝叶斯决策考虑如何基于这些概率和误判损失来选择最优的类> > 别标记
寻找一个判定准则 h:X → Y以最小化总体风险
贝叶斯判定准则:为最小化总体风险,只需在每个样本上选择那个能使条件风险R(c|x)最小的类别标记
被称为贝叶斯最优分类器,与之对应的总体风险R(h*)称为贝叶斯风险
1- R(h*)反映了分类起所能达到的最好性能,即通过机器学习所能产生的模型精度的理论上限
1. 贝叶斯决公式
- 在样本较多的时候,满足类条件概率的属性取值会非常多,比如:P(B1, B2, B3 | A) 条件下,B1取值为b1个, B2取值为b2个,B3取值为b3个,最终需要统计的样本为 ( x1 * x2 * x3 )个
- 条件概率属性取值过多, 会导致样本空间会非常大
- 在样本较少的情况下,同时满足多个的条件概率可能为0, 但并不能代表真正的概率值
2. 使用西瓜数据集
3. 朴素贝叶斯
- 朴素贝叶斯分类器采用了
属性条件独立性假设:每个属性独立地对分类结果发生影响 - 有个别属性相关也可以使用朴素贝叶斯分类器
- 但具有
强相关性的条件,朴素贝叶斯公式不成立 - 朴素贝叶斯,使得概率为0的条件大大减少,使其更接近于真实的值,在经过
拉普拉斯修正,其概率不会为0
3. 拉普拉斯修正
-
若某个属性值在训练集中没有而在测试集中出现,则直接计算会出现问题
-
比如“敲声=清脆”测试例,训练集中没有该样例,因此连乘式计算的概率值为0
-
无论其他属性上明显像好瓜,分类结果都是“好瓜=否”,这显然不合理
-
为了避免
其他属性携带的信息被训练集中未出现的属性值抹去,在估计概率值时通常要进行拉普拉斯修正
令N表示训练集D中可能的类别数,Ni表示第i个属性可能的取值数,则修正
4. 代码
import pandas as pd
import numpy as np
def gaussian_func(x, miu, rou):
"""
假设概率分布遵循正太分布(高斯分布)
:param x: 变量
:param miu: 高斯分布的均值
:param rou: 高斯分布的方差
:return: 返回x在高斯分步中, 概率的值
"""
return (1 / (np.sqrt(2 * np.pi) * rou)) * np.exp(-((x - miu) ** 2) / (2 * rou ** 2))
pass
# 将数据集根据标记划分为子集
def split_data(data_frame, feature, feature_value):
"""
1. 对每一行数据进行处理,将满足 data.iloc[i, :][feature] == feature 属性值满足的时候
2. 取出这一行, 转化为列表, 并添加到列表中, 形成二维数组
3. 对二维数组进行处理, 将其转化为DataFrame类型
:param data_frame:
:param feature:
:param feature_value:
:return:
"""
sub_list = []
data_len = len(data_frame)
# 对每一行进行处理
for i in range(data_len):
if data_frame.iloc[i, :][feature] == feature_value:
temp_list = (data_frame.iloc[i, :])
sub_list.append(temp_list)
# 形成DateFrame类型数据
sub_data_frame = pd.DataFrame(sub_list, columns=data_frame.columns)
return sub_data_frame
pass
def get_p_laplacian(data_frame):
"""
统计样本离散样本的属性以及 计算 连续属性的 均值方差
1. 取每一列的所有属性值,形成一个 列属性取值列表 字典 格式为{key: [v1, v2, ... ]} 不包括连续值属性, 连续值属性不缺失
2. 计算修正后的先验概率
3. 将属性集按照分类划分为子集
4. 对每一个子集进行处理, 分别计算 不同类中 下的 离散属性值概率, 和连续属性值参数
5. 对 列属性取值列表 在不同属性列下的取值进行遍历,计算修正后的概率 {"是": {"色泽": {"青绿": 0.112233, ... }, "触感": {... }, ...}
# , "否": {{"色泽": {"青绿": 0.112233, ... }, "触感": {... }, ...}}}
6. 对连续属性值 计算均值和方差, 放到分类后的字典中 为 {"是": {"密度": {"miu": 0.1, "rou": 0.2}}, "否": {... }}
:param data_frame: DataFrame类型数据
:return: 返回离散字典 和 连续字典
"""
# 计算先验概率
priority_probability = {}
# 数据集的长度
data_len = len(data_frame.iloc[:, 0])
# 分类的列名
class_column = data_frame[data_frame.columns[-1]]
# 统计类的个数
class_len = len(class_column.value_counts().keys())
# 拉普拉斯修正后的先验概率
for key, value in class_column.value_counts().items():
priority_probability[key] = (value + 1) / (data_len + class_len)
# 统计离散属性, 属性列名和离散属性的取值,格式为{key: [v1, v2, ... ]}
column_dict = {}
for item in list(data_frame.columns)[0: -1]: # 不统计最后类那一列
column_dict[item] = []
for key in column_dict.keys():
if not isinstance(data_frame.loc[0, key], (np.int64, np.float64)):
column_dict[key] = list(data_frame[key].value_counts().keys())
# 统计分类属性下的概率
discrete_probability_dict = {} # 离散属性字典,离散属性取值的概率 格式 {"是": {"色泽": {"青绿": 0.112233, ... }, "触感": {... }, ...}
# , "否": {{"色泽": {"青绿": 0.112233, ... }, "触感": {... }, ...}}}
consecutive_probability_dict = {} # 连续属性函数参数的字典 对于高斯函数为: {"是": {"密度": {"miu": 0.1, "rou": 0.2}}, "否": {...}}
# 建立分类下的字典
for key in priority_probability.keys():
discrete_probability_dict[key] = {}
consecutive_probability_dict[key] = {}
# 按照分类, 将数据集进行划分
for key in priority_probability.keys():
sub_data = split_data(data_frame, data_frame.columns[-1], key)
# 对分好类的数据子集进行处理
for col in list(sub_data.columns)[0: -1]: # 取属性列
sub_data_len = len(sub_data) + len(column_dict[col]) # 拉普拉斯修正, 分母为 数据集长度 + 属性类别的个数
tmp_dict = {} # 属性列 和 属性的 取值 格式: {"青绿": 0.4, "乌黑": 0.5 }
# 计算离散值的概率
if not isinstance(list(sub_data[col])[0], (float, int)): # 取其中的离散属性
# 取这一列 属性取值 和 取值的个数 如 {"青绿": 3, "乌黑": 2, "浅白": 1}
value_counts_dict = dict(sub_data[col].value_counts().items())
# 对每个属性的值都进行计算, 比如 {"色泽": ["青绿", "乌黑", "浅白"]}, 同时进行拉普拉斯修正
for key_1 in column_dict[col]: # 对每一列属性的取值都进行计算, 同时进行拉普拉斯修正
# 属性值,在子集中
if key_1 in value_counts_dict.keys():
tmp_dict[key_1] = (value_counts_dict[key_1] + 1) / sub_data_len
# 属性值,不再子集中
else:
tmp_dict[key_1] = 1 / sub_data_len
# 添加到离散字典中 为 {"是": {"色泽": tmp_dict}}
discrete_probability_dict[key][col] = tmp_dict
# 计算离散值, 只计算离散值高斯函数的 均值 和 标准差
else:
# 计算均值
nums = list(sub_data[col])
average_num = sum(nums) / sub_data_len
# 计算方差
tmp = 0
for num in nums:
tmp += (num - average_num) ** 2
if len(sub_data) == 1:
rou = np.sqrt(tmp / len(sub_data))
else:
rou = np.sqrt(tmp / (len(sub_data) - 1))
# 方差为0 时, 此时可能数据集属性取值中只有一个属性取值
rou = (1 if rou == 0.0 else rou)
# 添加到字典
tmp_dict = {"miu": average_num, "rou": rou}
# 添加到连续值字典 格式为: {"是": {"密度": {"miu": 0.1, "rou": 0.2}}, "否": {... }}
consecutive_probability_dict[key][col] = tmp_dict
return priority_probability, discrete_probability_dict, consecutive_probability_dict
# 创建测试数据字典
def create_test_list_dict(data):
"""
将测试集 DataFrame类型的数据, 转化为[{"色泽": "乌黑", "根蒂": "蜷缩", ... "密度": 0.697, ... }]
:param data:
:return:
"""
test_list = []
for i in range(len(data.iloc[:, 0])):
tmp_dict = {}
for column in list(data.columns):
tmp_dict[column] = data.loc[i, column]
test_list.append(tmp_dict)
return test_list
pass
def predict_test(priori_probability_dict, discrete_probability_dict, conse_probability_dict, test_list_dict):
"""
对测试字典进行预测,根据概率的大小进行分类
1. 首先对分类词典进行遍历, 遍历每一个类, 计算其概率
2. 对每一个类设置 类: 概率 键值对, 格式为: {"类1": 0.5, "类2": 0.5, "类3": ....}
3. 再数组中挑选最优的概率, 并统计分类成功的比率
:param priori_probability_dict:
:param discrete_probability_dict:
:param conse_probability_dict:
:return:
"""
RIGHT_CNT = 0
DATA_LEN = len(test_list_dict)
# 对每一个测试字典进行测试
for d in test_list_dict:
probability_value = 1
probability_clc_str = ""
probability_clc_str_dict = {}
# 对每一个类计算概率, 保存到字典中, 类概率字典为: {'否': 7.722360621178052e-05, '是': 0.02563102452974069}
p_dict = {}
for key in priori_probability_dict.keys():
probability_value *= priori_probability_dict[key]
probability_clc_str += " * " + str(priori_probability_dict[key])
for key_1 in discrete_probability_dict[key].keys():
probability_value *= discrete_probability_dict[key][key_1][d[key_1]]
probability_clc_str += " * " + str(discrete_probability_dict[key][key_1][d[key_1]])
for key_2 in conse_probability_dict[key].keys():
miu = conse_probability_dict[key][key_2]["miu"]
rou = conse_probability_dict[key][key_2]["rou"]
tmp_p = gaussian_func(d[key_2], miu, rou)
probability_value *= tmp_p
probability_clc_str += " * " + str(tmp_p)
# 保存到字典中
p_dict[key] = probability_value
probability_clc_str_dict[key] = probability_clc_str
# 每次循环,初始化参数
probability_value = 1
probability_clc_str = ""
# 挑选最优的概率
best_class = list(p_dict.keys())[0]
best_class_value = p_dict[best_class]
for key in p_dict.keys():
if p_dict[key] > best_class_value:
best_class = key
if best_class == d["好瓜"]:
RIGHT_CNT += 1
print("预测: {0}, 实际: {1} ".format(best_class, d["好瓜"]))
for key, value in p_dict.items():
print("类: ", key, ", 概率: ", value)
# print("计算过程: ", positive_s_dict[key])
return RIGHT_CNT / DATA_LEN
pass
def main():
data = pd.read_excel("西瓜数据集Trainning.xlsx")
p, d, c = get_p_laplacian(data)
# 显示建立的字典
print("先验概率: \n", p, "\n离散属性类条件概率: \n", d, "\n连续属性高斯函数参数的值: \n", c)
# print("consecutive: ", gaussian_func(0.697, c["是"]["密度"]["miu"], c["是"]["密度"]["rou"]), c["是"]["密度"]["miu"],\
# c["是"]["密度"]["rou"])s
data_test = pd.read_excel("西瓜数据集Test.xlsx")
# data_test = pd.read_excel("西瓜数据集Trainning.xlsx")
test_list_dict = create_test_list_dict(data_test)
# 显示测试列表
print(test_list_dict)
for i in test_list_dict:
print("测试实例:", i)
rate = predict_test(p, d, c, test_list_dict)
print("正确率维为: ", rate)
pass
if __name__ == '__main__':
main()
5. 结果
5.1 训练数据集
5.2 训练数据集
5.3 结果
先验概率:
{'否': 0.5263157894736842, '是': 0.47368421052631576}
离散属性类条件概率:
{'否': {'色泽': {'青绿': 0.3333333333333333, '乌黑': 0.25, '浅白': 0.4166666666666667}, '根蒂': {'蜷缩': 0.3333333333333333, '稍蜷': 0.4166666666666667, '硬挺': 0.25}, '敲声': {'浊响': 0.4166666666666667, '沉闷': 0.3333333333333333, '清脆': 0.25}, '纹理': {'清晰': 0.25, '稍糊': 0.4166666666666667, '模糊': 0.3333333333333333}, '脐部': {'凹陷': 0.25, '稍凹': 0.3333333333333333, '平坦': 0.4166666666666667}, '触感': {'硬滑': 0.6363636363636364, '软粘': 0.36363636363636365}}, '是': {'色泽': {'青绿': 0.36363636363636365, '乌黑': 0.45454545454545453, '浅白': 0.18181818181818182}, '根蒂': {'蜷缩': 0.5454545454545454, '稍蜷': 0.36363636363636365, '硬挺': 0.09090909090909091}, '敲声': {'浊响': 0.6363636363636364, '沉闷': 0.2727272727272727, '清脆': 0.09090909090909091}, '纹理': {'清晰': 0.7272727272727273, '稍糊': 0.18181818181818182, '模糊': 0.09090909090909091}, '脐部': {'凹陷': 0.5454545454545454, '稍凹': 0.36363636363636365, '平坦': 0.09090909090909091}, '触感': {'硬滑': 0.7, '软粘': 0.3}}}
连续属性高斯函数参数的值:
{'否': {'密度': {'miu': 0.4961111111111111, 'rou': 0.19471867170641624}, '含糖率': {'miu': 0.1542222222222222, 'rou': 0.10779468653159321}}, '是': {'密度': {'miu': 0.5737500000000001, 'rou': 0.12921051483086482}, '含糖率': {'miu': 0.27875, 'rou': 0.10092394590553255}}}
[{'色泽': '青绿', '根蒂': '蜷缩', '敲声': '浊响', '纹理': '清晰', '脐部': '凹陷', '触感': '硬滑', '密度': 0.697, '含糖率': 0.46, '好瓜': '是'}, {'色泽': '青绿', '根蒂': '蜷缩', '敲声': '浊响', '纹理': '稍糊', '脐部': '稍凹', '触感': '硬滑', '密度': 0.719, '含糖率': 0.103, '好瓜': '否'}]
测试实例: {'色泽': '青绿', '根蒂': '蜷缩', '敲声': '浊响', '纹理': '清晰', '脐部': '凹陷', '触感': '硬滑', '密度': 0.697, '含糖率': 0.46, '好瓜': '是'}
测试实例: {'色泽': '青绿', '根蒂': '蜷缩', '敲声': '浊响', '纹理': '稍糊', '脐部': '稍凹', '触感': '硬滑', '密度': 0.719, '含糖率': 0.103, '好瓜': '否'}
预测: 是, 实际: 是
类: 否 , 概率: 7.722360621178052e-05
类: 是 , 概率: 0.02563102452974069
预测: 否, 实际: 否
类: 否 , 概率: 0.007575773381706271
类: 是 , 概率: 0.003941353700990114
正确率维为: 1.0
6. 参考书籍
周志华 - 西瓜书 - 《机器学习》